计算方法B.裴玉茹.06.线性方程组(2)

Posted on Edited on In Views:
矩阵收敛性、不动点迭代方法、收敛性证明、迭代方法比较（雅各比方法、高斯赛德尔方法、松弛方法）、Kahan 定理、Ostrowski-Reich 定理、误差分析、
  • PPT（线性方程组）

线性方程组

4. 迭代求解

(1) 矩阵收敛

  • \(n\times n\) 矩阵收敛：\(\lim_{k\to\infty}(A^{k})_{ij}=0\)

等价命题

  • 如下命题等价
    • \(A\) 是收敛矩阵
    • 对任意自然范数，\(\lim_{n\to\infty}\Vert{A^{n}}\Vert=0\)
    • \(\rho(A)<1\)
    • \(\lim_{n\to\infty}A^{n}x=0\)

例子

  • 收敛矩阵

\[ A=\begin{pmatrix} \dfrac{1}{2}&0\\ \dfrac{1}{4}&\dfrac{1}{2}\\ \end{pmatrix}, A^{k}=\begin{pmatrix} \dfrac{1}{2^{k}}&0\\ \dfrac{k}{2^{k+1}}&\dfrac{1}{2^{k}}\\ \end{pmatrix} \]

(2) 线性方程组不动点迭代

  • \(Ax=b\) 构造不动点迭代函数 \(x=Tx+c\)

雅各比迭代方法

\[ x_{k+1}=-D^{-1}(L+U)x_{k}+D^{-1}b \]

高斯塞德尔方法

\[ x_{k+1}=-D^{-1}Lx_{k+1}-D^{-1}Ux_{k}+D^{-1}b \]

\[ x_{k+1}=-(D+L)^{-1}Ux_{k}+(D+L)^{-1}b \]

(3) 迭代方法的收敛性

谱半径定理

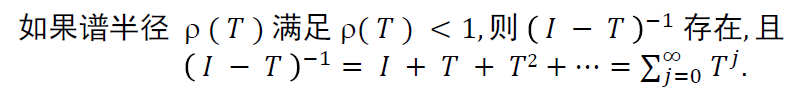
  • 证明

收敛定理

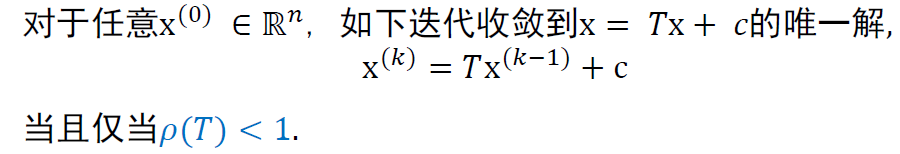
  • 充分性

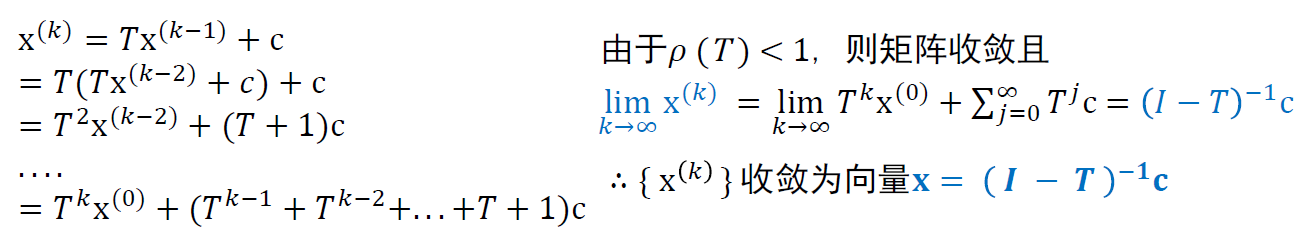
  • 必要性：通过证明 \(A\) 是收敛矩阵得到 \(\rho(A)<1\)

误差界

  • 证明方法和单变量迭代类似

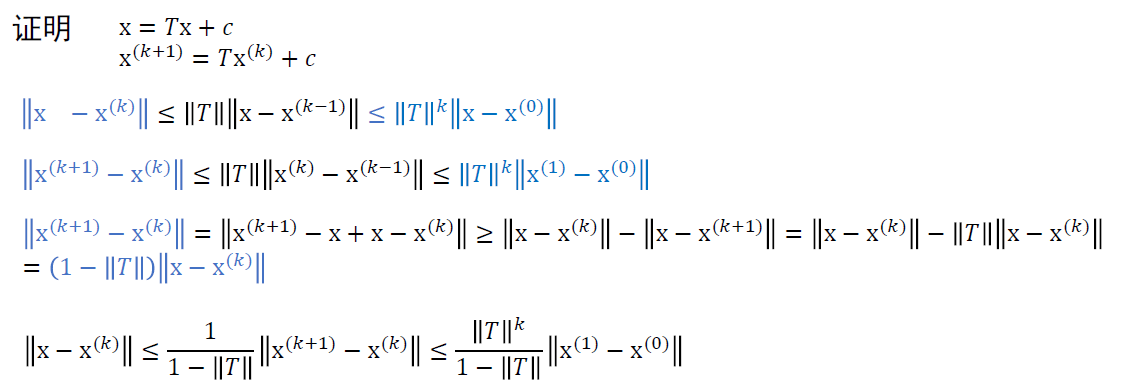
(4) 收敛性证明

雅各比方法、高斯塞德尔方法

  • 证明：note
    • 使用严格对角占优的条件证明谱半径小于 1

(5) 迭代方法比较

Stein Rosenberg 定理

  • 如果 \(a_{ij}\le0,i\ne j,a_{ii}>0,i=1,\cdots,n\)，则如下命题仅有一项成立
    • \(0\le\rho(T_g)\le\rho(T_j)<1\)
    • \(1\le\rho(T_j)\le\rho(T_g)\)
    • \(0=\rho(T_g)=\rho(T_j)\)
      • 收敛
    • \(1=\rho(T_g)=\rho(T_j)\)
      • 不收敛：误差很难降低
  • 谱半径越小收敛越快
    • 一个方法收敛，两种方法都收敛，Gauss-Seidel 方法收敛更快
    • 一个方法发散，二者皆发散.，高斯赛德尔方法发散更快

(6) 松弛方法

  • SOR
  • 下面的定义和书上是一致的，\(r_i\) 里面包含了 \(i=j\) 的一项

image-20211102231549351

  • 对于特定的正数 \(w\) , 可以减少残差向量的范数，获得更快的收敛速度
    • \(0<w<1\)：欠松弛
      • 使得 GS 下某些不收敛线性方程组收敛
    • \(w=1\)：Gauss-Seidel
    • \(w>1\)：过松弛（SOR）
      • 使得 GS 下某些收敛线性方程组收敛更快

Kahan 定理

  • 对于 SOR 方法，如果 \(a_{ii}\ne0,i=1,\cdots,n\)，则 \(\rho(T_w)\ge\vert{w-1}\vert\)
证明
  • 化成 \(x=Tx+c\) 的形式

\[ x_{k+1}=(\omega L+D)^{-1}\big((1-\omega)D-\omega U\big)x_{k}+\omega(\omega L+D)^{-1}b \]

  • 记 \(H=(\omega L+D)^{-1}\big((1-\omega)D-\omega U\big)\)

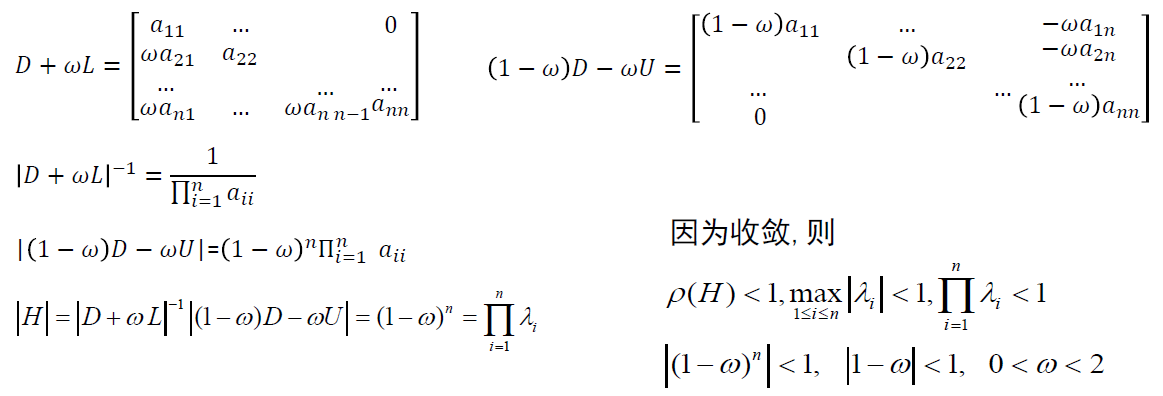
推论
  • SOR 方法收敛的必要条件是 \(\vert{w-1}\vert<1\)，即 \(0<w<2\)

Ostrowski-Reich 定理

  • 如果 \(A\) 是正定矩阵且 \(0<w<2\)，则 SOR 方法对于任意初始近似向量 \(x_0\) 收敛
    • 正定：定义中包括共轭对称
证明
  • 思路：证明 \(\vert\lambda\vert<1\Leftrightarrow{\lambda}^2<1\)

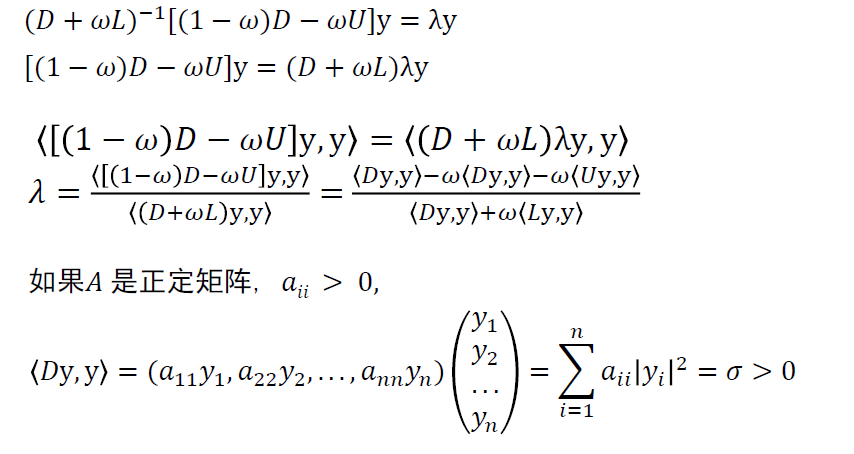
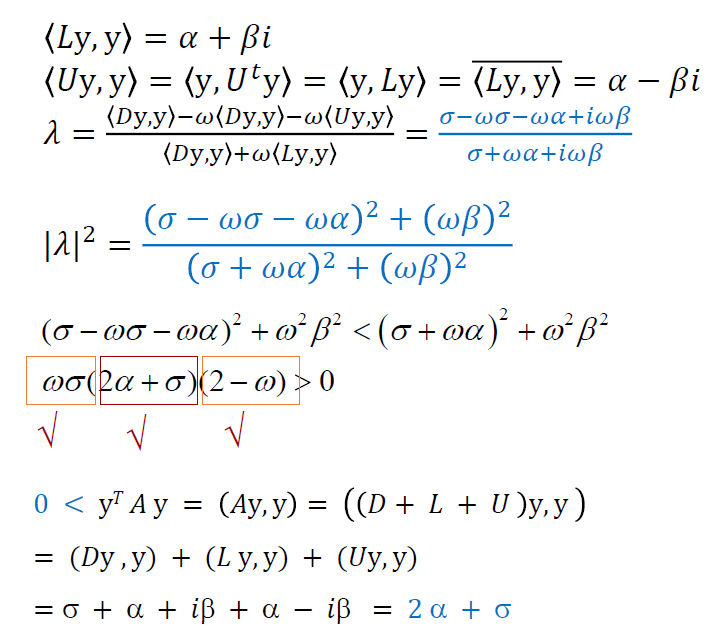
最优 w

  • 如果 \(A\) 是正定三对角线矩阵，则 \(\rho(T_g)=\rho^{2}(T_j)<1\)，SOR方法 \(\rho(T)=w-1\)，最优的 \(w\) 值为

\[ w=\dfrac{2}{1-\sqrt{1-\rho^{2}(T_j)}} \]

  • 三对角线矩阵：只有对角线和与其相邻的两条对角线有非零元素

(7) 误差分析

\[ \dfrac{\Vert{x-x_a}\Vert}{\Vert{x}\Vert}\le\Vert{A^{-1}}\Vert\Vert{A}\Vert\cdot\dfrac{\Vert{r}\Vert}{\Vert{b}\Vert} \]

  • 条件数

\[ K(A)=\mathrm{cond}(A)=\Vert{A^{-1}}\Vert\Vert{A}\Vert \]

  • 病态与良态
    • 当 \(K(A)\) 接近 \(1\) 时，矩阵 \(A\) 是良态矩阵
    • 当 \(K(A)\) 显著大于 \(1\) 时，矩阵是病态的
  • 病态矩阵示例
    • 希尔伯特矩阵：\((H_{n})_{ij}=\dfrac{1}{i+j-1}\)

条件数近似

近似方法 1
  • \(t\) 位算术，残差向量 \(r\) 的近似值为 \(\Vert{r}\Vert\approx10^{-t}\Vert{A}\Vert\Vert{x}\Vert\)
  • 那么条件数的近似值 \(K(A)=\dfrac{\Vert{\tilde{y}}\Vert}{\Vert{\tilde{x}}\Vert}10^{t}\)，其中 \(\Vert{\tilde{y}}\Vert=A^{-1}r\)

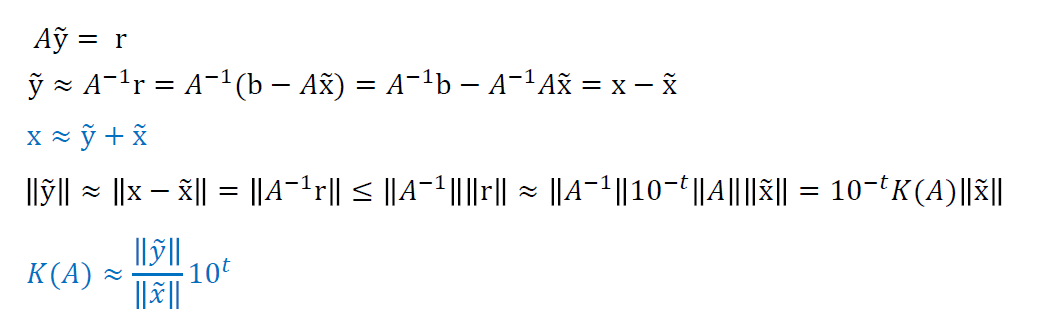
迭代算法的优化
  • 一般来说， \(\tilde{x}+\tilde{y}\) 比 \(\tilde{x}\) 更精确
  • 步骤

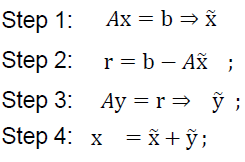
2 范数

\[ K(A)_2=\sqrt{\dfrac{\lambda_{max}(A^{T}T)}{\lambda_{min}(A^{T}T)}} \]

  • \(Ax_1=\lambda_1 x_1\) 那么则有 \(A^{-1}x=\dfrac{1}{\lambda_1}x_1\)

不等式