计算方法B.裴玉茹.06.线性方程组

• PPT（线性方程组）

线性方程组

• 向量范数、矩阵范数、算子范数（诱导范数 / 自然范数）
  • note

1. 向量范数

定义

• 3 个条件
  • 正定性、齐次性、三角不等式

欧式范数

\[ \Vert{x}\Vert_1=\sum_{i=1}^{n}{\vert{x_i}\vert} \]

\[ \Vert{x}\Vert_2=\sqrt{\sum_{i=1}^{n}{\vert{x_i}\vert^2}} \]

\[ \Vert{x}\Vert_2=\left(\sum_{i=1}^{n}{\vert{x_i}\vert^p}\right)^{\dfrac{1}{p}} \]

\[ \Vert{x}\Vert_\infty=\max_{1\le i\le n}{\vert{x_i}\vert} \]

• 示意图
  • 这也说明了 \(\Vert{x}\Vert_{a}\le\Vert{x}\Vert_{b}(a>b\in\mathbb{N})\)

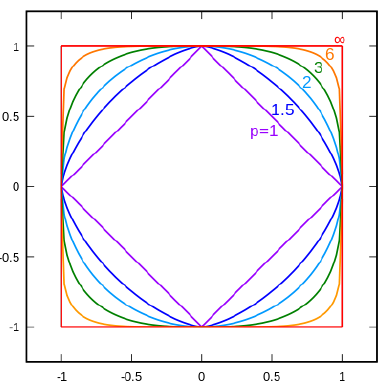
• 2范数图示

• 无穷范数图示

柯西不等式

• Cauchy-Buniakowsky-Schwarz 不等式

• \(x=(x_1,\cdots,x_n)^{T},y=(y_1,\cdots,y_n)^{T}\)，则有如下式子成立

\[ x^{T}y=\sum_{i=1}^{n}x_iy_i\le\sum_{i=1}^{n}x_i^2\sum_{i=1}^{n}y_i^2=\Vert{x}\Vert_2\cdot\Vert{y}\Vert_2 \]

• 证明
  • 构造如下不等式，展开然后令 \(\lambda=\dfrac{\Vert{x}\Vert_2}{\Vert{y}\Vert_2}\) 即可

\[ \Vert{x-\lambda y}\Vert_2\ge0 \]

关于范数收敛

定理与证明

• 证明

范数之间的关系

\[ \Vert{x}\Vert_\infty\le\Vert{x}\Vert_2\le\sqrt{n}\Vert{x}\Vert_\infty \]

• 图示

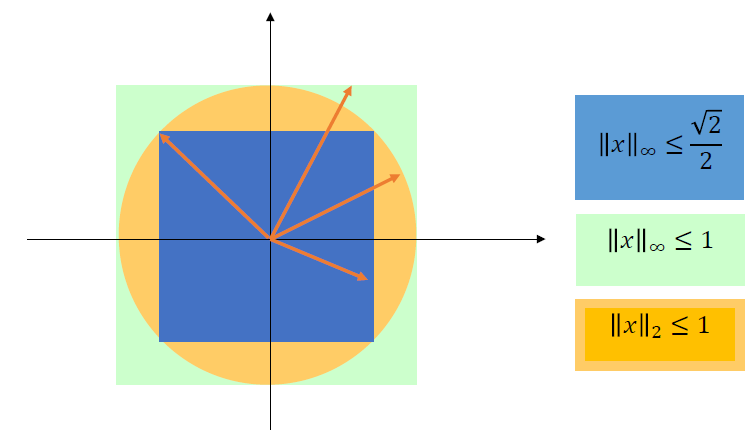
证明

\[ j=\mathop{\arg\max}_{1\le i\le n}\vert{x_i}\vert \]

• \(\Vert{x}\Vert_\infty\le\Vert{x}\Vert_2\)

\[ \Vert{x}\Vert_\infty^2=\left(\max_{1\le i\le n}\vert{x_i}\vert\right)^2=x_j^2\le\sum_{i=1}^{n}x_i^2\le\Vert{x}\Vert_2^2 \]

• \(\Vert{x}\Vert_2\le\sqrt{n}\Vert{x}\Vert_\infty\)

\[ \Vert{x}\Vert_2^2=\sum_{i=1}^{n}x_i^2\le\sum_{i=1}^{n}x_j^2=nx_j^2=n\Vert{x}\Vert_\infty^2 \]

收敛等价

• 说明了对于两个范数 \(\Vert{x}\Vert_a,\Vert{x}\Vert_b\)，存在 \(m,n\) 使得 \(m\Vert{x}\Vert_b\le\Vert{x}\Vert_a\le n\Vert{x}\Vert_b\) 成立

2. 矩阵范数

• 4 个条件

矩阵范数的自然范数定义

\[ \Vert{A}\Vert=\max_{\Vert{x}\Vert=1}\Vert{Ax}\Vert=\max_{\Vert{x}\Vert\ne0}\dfrac{\Vert{Ax}\Vert}{\Vert{x}\Vert} \]

• 推论：对于任意向量 \(\Vert{x}\Vert\ne0\)，矩阵 \(A\) 及其自然范数 \(\Vert{A}\Vert\)，有如下式子成立
  • 定义即证

\[ \Vert{A}\Vert\Vert{x}\Vert\ge\Vert{Ax}\Vert \]

• 推论：\(\Vert{AB}\Vert\le\Vert{A}\Vert\Vert{B}\Vert\)

\[ \begin{aligned} \Vert{AB}\Vert&=\max_{\Vert{x}\Vert=1}\Vert{ABx}\Vert\\ &=\max_{\Vert{x}\Vert=1}\Vert{A(Bx)}\Vert\\ &\le\max_{\Vert{x}\Vert=1}\Vert{A}\Vert\Vert{Bx}\Vert\\ &=\Vert{A}\Vert\max_{\Vert{x}\Vert=1}\Vert{Bx}\Vert\\ &=\Vert{A}\Vert\Vert{B}\Vert\\ \end{aligned} \]

• 矩阵范数表示在矩阵 \(A\) 的作用下向量长度的最大拉伸

1 范数

\[ \Vert{A}\Vert_{1}=\max_{j}\left(\sum_{i=1}^{n}\vert{a_{ij}}\vert\right) \]

• \(\Vert{A}\Vert_{1}\) 是自然范数
  • 证明

无穷范数

\[ \Vert{A}\Vert_{\infty}=\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right) \]

• \(\Vert{A}\Vert_{\infty}\) 是自然范数
  • 证明

补充

• 和书上不一样的证明方式，证明如下部分的时候

\[ \Vert{A}\Vert_{\infty}\ge\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right) \]

• 只需要构造一个向量 \(x\)，满足如上式子即可
• 令 \(p\) 为满足如下式子的整数

\[ \mu=\sum_{j=1}^{n}\vert{a_{pj}}\vert=\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right) \]

• 构造 \(x\) 如下

\[ x_j=\left\{\begin{array}{ll} 1,&\mathrm{if}\;a_{pj}\ge0\\ -1,&\mathrm{if}\;a_{pj}<0\\ \end{array}\right. \]

• 那么有 \(\Vert{x}\Vert_{\infty}=1,a_{pj}x_j=\vert{a_{pj}}\vert_{\infty}\)

\[ \begin{aligned} \Vert{Ax}\Vert_{\infty}&=\max_{1\le i\le n}\left\vert{\sum_{j=1}^{n}a_{ij}x_j}\right\vert\\ &\ge\left\vert{\sum_{j=1}^{n}a_{pj}x_j}\right\vert\\ &=\sum_{j=1}^{n}\left\vert{a_{pj}}\right\vert\\ &=\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right) \end{aligned} \]

2 范数 / 谱范数

• \(A\) 的谱范数定义为 \(A^HA\) 的最大特征值的平方根

\[ \Vert{A}\Vert_{2}=\sqrt{\lambda_{max}(A^HA)} \]

• \(A^{H}\) 表示矩阵 \(A\) 的共轭转置，如果是实矩阵，等价为 \(A^{T}\)
• \(\Vert{A}\Vert_{2}\) 是自然范数
  • 参考资料

证明

• 以下只在实数域内证明
  • 复数域同理
• \(A^{T}A\) 半正定，因此 \(A^{T}A\) 的特征值都为非负数

\[ x^{T}A^{T}Ax=(Ax)^{T}(Ax)=\Vert{Ax}\Vert_2^{2}\ge0 \]

• 记矩阵 \(A^{T}A\) 的特征值为 \(\lambda_1\ge\lambda_2\ge\cdots\ge\lambda_n\ge0\)，对应的单位特征向量为 \(x_1,\cdots,x_n\)
  • 零特征值则对应一个与之前向量都正交的单位向量
• 对于任意的单位向量 \(u\in\mathbb{R}^{n}\)，其可以表示为

\[ u=a_1x_1+\cdots+a_nx_n \]

• 可以得到

\[ u^{T}u=a_1^2+\cdots+a_n^2=1 \]

\[ A^TAu=a_1\lambda_1x_1+\cdots+a_n\lambda_nx_n \]

\[ \begin{aligned} \Vert{Au}\Vert_2^2&=u^TA^TAu\\ &=u^T(a_1\lambda_1x_1+\cdots+a_n\lambda_nx_n)\\ &=\lambda_1a_1^2+\cdots+\lambda_na_n^2\\ &\le\lambda_1(a_1^2+\cdots+a_n^2)\\ &=\lambda_1\\ \end{aligned} \]

• 所以我们得到

\[ \\\max_{\Vert{x}\Vert_2=1}\Vert{Ax}\Vert_2\le\sqrt{\lambda_1} \]

• 同时我们有

\[ \Vert{Ax_1}\Vert_2^2=x_1^TA^TAx_1=x_1^T\lambda_1x_1=\lambda_1 \]

• 所以

\[ \max_{\Vert{x}\Vert_2=1}\Vert{Ax}\Vert_2\ge\Vert{Ax_1}\Vert_2=\sqrt{\lambda_1} \]

• 因此

\[ \max_{\Vert{x}\Vert_2=1}\Vert{Ax}\Vert_2=\sqrt{\lambda_1} \]

F 范数

• Frobenius 范数

\[ \Vert{A}\Vert_{F}=\sqrt{\sum_{i=1}^{n}\sum_{j=1}^{n}\vert{a_{ij}}\vert^{2}}=\sqrt{\mathrm{tr}(A^{T}A)} \]

性质 1

\[ \Vert{A}\Vert_{2}\le\Vert{A}\Vert_{F}\le\sqrt{n}\Vert{A}\Vert_{2} \]

• 证明：矩阵的迹等于矩阵所有特征值的和

性质 2

\[ \Vert{Ax}\Vert_{2}\le\Vert{A}\Vert_{F}\Vert{x}\Vert_{2} \]

• 证明（柯西不等式）

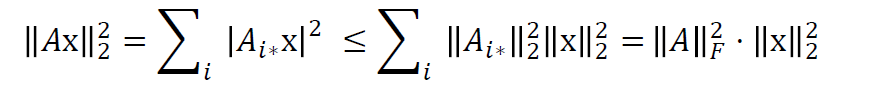
F 范数不是自然范数

• 考虑单位矩阵

\[ \Vert{I}\Vert_{F}=\sqrt{n}\ne\max_{\Vert{x}\Vert\ne0}\dfrac{\Vert{Ix}\Vert}{\Vert{x}\Vert}=1 \]

3. 特征值与特征向量

特征值

• 特征值 \(\lambda\)

\[ \det(A-\lambda I)=0 \]

特征向量

• 特征向量 \(x\)

\[ Ax=\lambda x \]

行列式

• 矩阵的行列式所有特征值的积
  • \(\det(\lambda I-A)=(\lambda-\lambda_1)\cdots(\lambda-\lambda_n)\)
  • 令 \(\lambda=0\) 即证

\[ \det(A)=\prod_{i=1}^{n}\lambda_i \]

迹

• 矩阵的迹等于所有特征值的和
  • 两种方式展开 \(\det(\lambda I-A)\) ，\(n-1\) 次项的系数相等
    • 特征值为根、硬展开
    • 硬展开降阶的时候，非对角线展开最多只有 \(n-2\) 次项

\[ \mathrm{tr}(A)=\sum_{i=1}^{n}a_{ii}=\sum_{i=1}^{n}\lambda_{i} \]

幂乘性质

• \(A^k\) 的特征值为 \(\lambda_1^k,\cdots,\lambda_n^k\)
• 如果矩阵 \(A\) 等于共轭转置矩阵 \(A^{H}\)，即厄米特矩阵，则所有特征值都是实数

\[ \begin{array}{c} (Ax)^{H}=(\lambda x)^{H}\Rightarrow x^{H}A^{H}=\bar{\lambda}x^{H}\\ x^{H}A^{H}x=\bar{\lambda}x^{H}x\\ 0=x^{H}A^{H}x-x^{H}Ax=(\lambda-\bar{\lambda})x^{H}x\\ \bar{\lambda}=\lambda\\ \end{array} \]

谱半径

\[ \rho(A)=\max_{1\le i\le n}\vert{\lambda_i}\vert \]

• 2范数定义

\[ \Vert{A}\Vert_2=\sqrt{\rho(A^{T}A)} \]

• 对任意自然范数

\[ \rho(A)\le\Vert{A}\Vert \]

• 证明
  • 取特征值对应的单位特征向量

\[ \vert{\lambda}\vert=\vert{\lambda}\vert\Vert{x}\Vert=\Vert{\lambda x}\Vert=\Vert{Ax}\Vert\le\Vert{A}\Vert \]