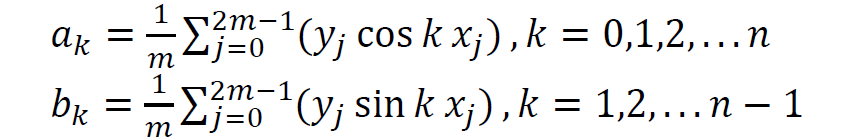计算方法B.裴玉茹.05.最小二乘(4)

Posted on Edited on In Views:
多项式近似、Gram-Schmidt 方法、车比雪夫多项式、有理函数近似、Pade 近似、三角多项式
  • 数值分析课本第 4 章（最小二乘） + PPT（最小二乘法）

最小二乘

  • PPT 补充

5. 多项式近似

  • 如何构造正交多项式 \(\phi_0,\cdots,\phi_n\)

(1) Gram-Schmidt 方法

  • \(\phi_0=1\)
  • \(\phi_1=x-B_1,B_1=\dfrac{\int_{a}^{b}xw(x)[\phi_0(x)]^2\;\mathrm{d}x}{\int_{a}^{b}w(x)[\phi_0(x)]^2\;\mathrm{d}x}\)
  • \(k\ge2\)
    • \(\phi_k=(x-B_k)\phi_{k-1}-C_k\phi_{k-2}\)
    • \(B_k=\dfrac{\int_{a}^{b}xw(x)[\phi_{k-1}(x)]^2\;\mathrm{d}x}{\int_{a}^{b}w(x)[\phi_{k-1}(x)]^2\;\mathrm{d}x}\)
    • \(C_k=\dfrac{\int_{a}^{b}xw(x)\phi_{k-1}(x)\phi_{k-2}(x)\;\mathrm{d}x}{\int_{a}^{b}w(x)[\phi_{k-2}(x)]^2\;\mathrm{d}x}\)

性质

  • 对于任意 \(n>0\)，利用 Gram-Schmidt 方法生成的多项式函数集合 \(\phi_0,\cdots,\phi_n\) 在区间 \([a,b]\) 上线性无关，而且对于任意的 \(k(k<n)\) 阶多项式，都有如下式子成立

\[ \int_a^bw(x)\phi_nQ_k(x)\;\mathrm{d}x=0 \]

证明
  • 线性无关：\(\phi_n\) 为 \(n\) 阶多项式即证
  • 式子：\(Q_k=\sum_{j=0}^{k}a_j\phi_j\)

Legendre 多项式

  • \([a,b]=[-1,1]\)
  • \(w(x)=1\)
  • \(\phi_0=1,\phi_1=x,\phi_2=x^2-\dfrac13,\cdots\)

(2) 车比雪夫多项式

\[ T_n(x)=\cos(n\arccos{x}) \]

  • Chebyshev 多项式
  • 在区间 \([-1,1]\) 上关于 \(w(x)=\dfrac{1}{\sqrt{1-x^2}}\) 正交

正交性

  • \(n\ne m\)

\[ \begin{aligned} &\int_{-1}^{1}\dfrac{\cos(n\arccos{x})\cos(m\arccos{x})}{\sqrt{1-x^2}}\;\mathrm{d}x\\ =&\int_{0}^{\pi}\cos(n\arccos{x})\cos(m\arccos{x})\;\mathrm{d}(\arccos{x})\\ =&\int_{0}^{\pi}\cos(n\theta)\cos(m\theta)\;\mathrm{d}\theta\\ =&\int_{0}^{\pi}\dfrac{1}{2}(\cos{(n+m)\theta}+\cos(n-m)\theta)\;\mathrm{d}x\\ =&0 \end{aligned} \]

  • \(n=m\)

\[ \dfrac{\pi}{2} \]

应用

  • 拉格朗日插值点
  • 降低近似多项式的阶数

拉格朗日插值点

降低多项式的阶

  • 利用至多 \(n-1\) 阶多项式，近似区间 \([−1,1]\) 上的任意 \(n\) 阶多项式

\[ \max_{x\in[-1,1]}\left\vert{\dfrac{1}{a_n}\Big(p_n(x)-p_{n-1}(x)\Big)}\right\vert\ge\dfrac{1}{2^{n-1}} \]

  • 利用切比雪夫插值的性质，令 \(p_n(x)-p_{n-1}(x)=a_n\tilde{T}_n\)，此时取到等号

(3) 比较

6. 有理函数近似

  • 多项式近似
    • 可以在闭合区间中以任意精度近似函数
    • 数值计算简单
      • 导数、积分、函数求值
    • 可能发生震荡
  • \(N\) 阶有理函数 \(r(x)=\dfrac{p(x)}{q(x)}\)
    • \(\deg(p(x))+\deg(q(x))=N\)
  • 在有理函数中,如果 \(p(x),q(x)\) 具有相近的阶数，则函数近似一般比多项式要好
  • 有理函数近似能够将误差均匀分布在整个区间中

Pade 近似

\[ r(x)=\dfrac{p(x)}{q(x)}=\dfrac{\sum_{i=0}^{n}p(x)}{\sum_{i=1}^{m}q(x)} \]

  • 一共 \(N+1\) 个参数
  • 假设 \(f(x)=\sum_{i=0}^{\infty}a_ix^i\)
    • \(q_0=1\)

\[ f(x)-r(x)=\dfrac{f(x)\sum_{i=0}^{m}q_ix^i-\sum_{i=0}^{n}p_ix^i}{\sum_{i=0}^{m}q_ix^i} \]

  • 选择参数，使得 \(f^{(k)}(0)-r^{(k)}(0)=0,k=0,\cdots,N\)
    • \(x=0\) 是 \(N+1\) 重根
    • 因此没有小于等于 \(N\) 阶的项
    • \(\sum_{i=0}^{k}a_iq_{k-i}=p_k,k=0,\cdots,N\)
      • \(N+1\)个线性方程，\(N+1\) 个未知量
      • 初始条件
        • \(p_{n+1}=\cdots=p_{N}=0\)
        • \(q_{m+1}=\cdots=q_{N}=0\)

7. 三角多项式

  • \([-\pi,\pi]\)
  • \(w(x)=1\)
  • \(\phi_i\) 正交，\(i=0,\cdots,2n-1\)

\[ \phi_0=\dfrac{1}{2} \]

\[ \phi_k=\cos{kx},k=1,\cdots,n \]

\[ \phi_{n+k}=\sin{kx},k=1,\cdots,n-1 \]

  • 傅里叶变换

\[ S_n(x)=\dfrac{1}{2}a_0+a_n\cos{nx}+\sum_{i=1}^{n-1}(a_k\cos{kx}+b_k\sin{kx}) \]

离散形式

  • \(2m\) 对数据，\(\{(x_j,y_j)\}_{j=0}^{2m-1}\)
    • \(x_j=-\pi+\dfrac{j}{m}\pi\)
  • 误差最小化：最小二乘

\[ E=\sum_{j=0}^{2m-1}(y_i-S_n(x_j))^2 \]

性质

  • 若 \(r\) 不是 \(2m\) 的倍数，则有

\[ \sum_{j=1}^{2m-1}\cos{rx_j}=0,\sum_{j=1}^{2m-1}\sin{rx_j}=0 \]

  • 若 \(r\) 不是 \(m\) 的倍数，则有

\[ \sum_{j=1}^{2m-1}\cos^2{rx_j}=m,\sum_{j=1}^{2m-1}\sin^2{rx_j}=m \]

  • 证明：欧拉公式

\[ e^{iz}=\cos{z}+\sin{z} \]

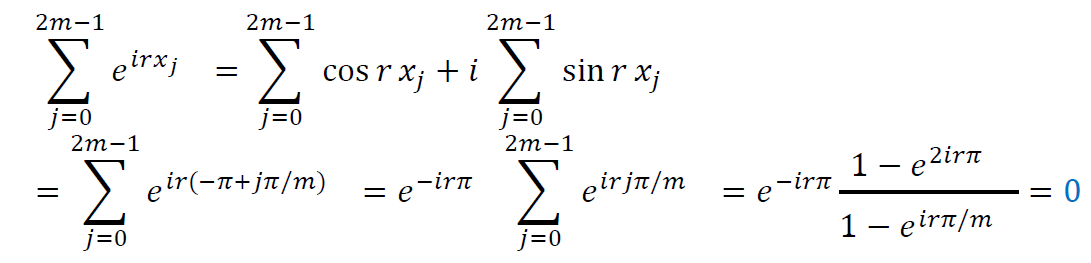
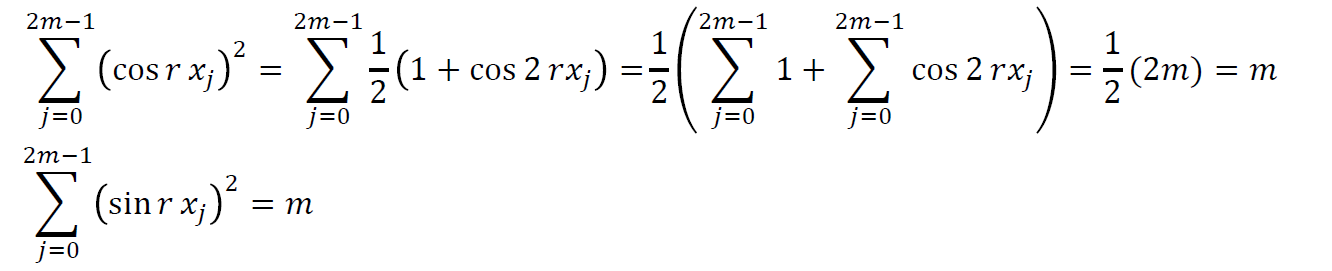
正交性

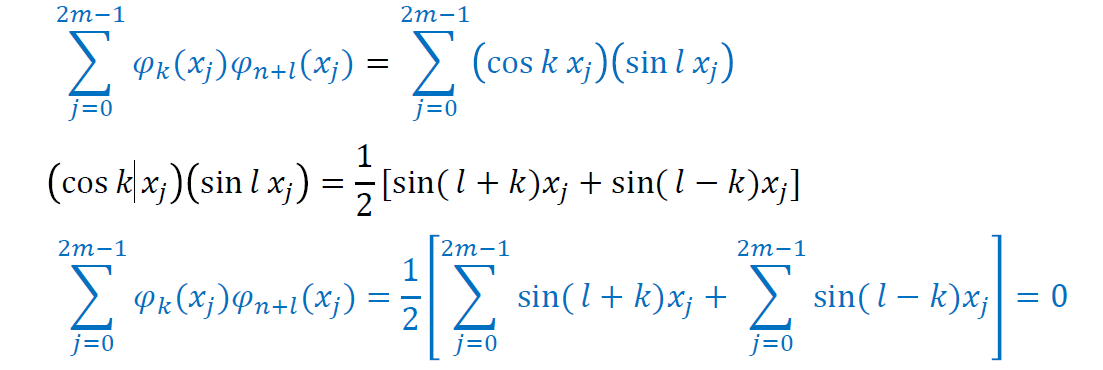
最小二乘误差

\[ E=\sum_{j=0}^{2m-1}(y_i-S_n(x_j))^2 \]

  • 偏导数为 0
    • 只剩下蓝色部分，其余都为 0

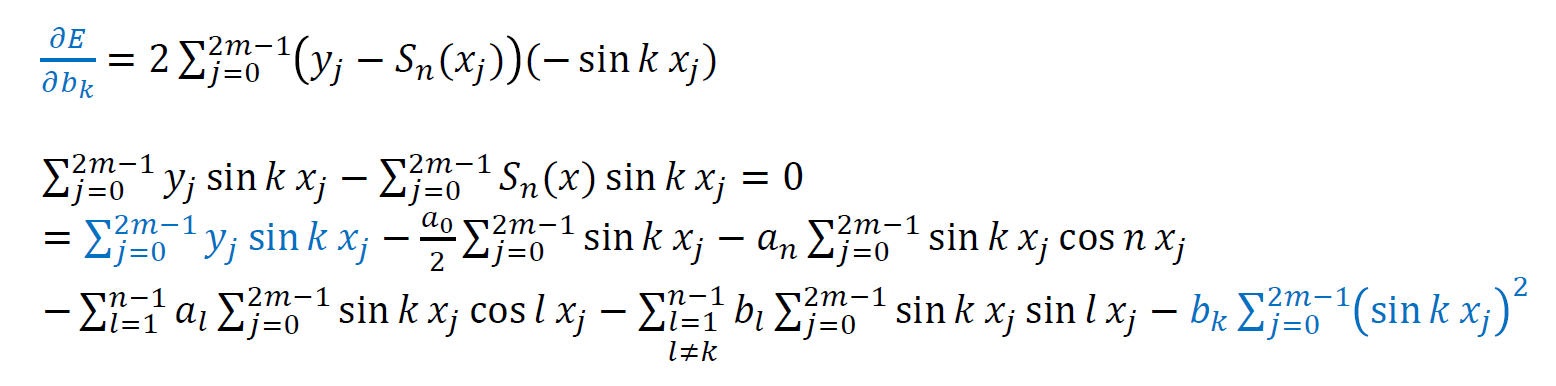
  • 于是我们能够得到 \(a_k,b_k\) 的表达式