计算方法B.裴玉茹.05.最小二乘(2)

Posted on Edited on In Views:
广义最小余项(GMRES)方法、非线性最小二乘、高斯牛顿法、Levenberg-Marquardt 方法（正则项）
  • 数值分析课本第 4 章（最小二乘） + PPT（最小二乘法）

最小二乘

4. 广义最小余项(GMRES)方法

4.1 Krylov 方法

  • GMRES 属于 Krylov 方法
    • 这些方法依赖精确的 Krylov 空间的计算
    • 该空间是向量 \(\{r,Ar,\cdots,A^{k}r\}\) 所张成的空间，\(r=b-A_0\) 为初始估计的余项
  • GMRES 的思想是在特殊矢量空间（即 Krylov 空间）中寻找初始估计的 \(x_0\) 的改进

算法

  • \(A:n\times n,Q_k:n\times k,H_k:(k+1)\times k\)
  • \(k<n\)

  • 算法解释
    • Krylov 空间由余项 \(r\) 和它与非奇异矩阵 \(A\) 的积所张成
    • 在该方法的第 \(k\) 步，我们加入 \(A^{k}r\) 以扩大 Krylov 空间，重新对基进行正交化，然后通过最小二乘获取改进并加到 \(x_0\) 中

  • 具体步骤解释

  • 代价最高的是最小二乘的计算，如果 \(h_{k+1,k}=0\)，则变成精确求解

误差分析

  • 后向误差 \(\Vert{b-Ax_k}\Vert_2\) 随着 \(k\) 单调下降
    • 由于最小二乘问题第 \(k\) 步在 \(k\) 维 Krylov 空间中最小化 \(\Vert{b-Ax_{add}}\Vert_2\) 得到 \(x_{add}\)
    • 当 GMRES 运行下去，Krylov 空间逐步变大，因而下一个近似不会变差

实现的一些问题

  • 最小二乘的步骤只有在需要求近似解 \(x_k\) 的时候才需要用到，因此并不是每一次都需要求
    • \(x_k\) 只与之前的 \(x_0\)相关
  • 条件数影响问题求解的话，可以使用豪斯霍尔德正交变换替换格拉姆-施密特正交变换
  • GMRES 的典型用途是用于大规模稀疏的 \(n\times n\) 矩阵 \(A\)
    • 理论上，算法经过 \(n\) 步终止，只要 \(A\) 是非奇异矩阵就可以得到解 \(x\)
    • 在大多数情况下，目标是仅仅运行 \(k\) 步，\(k\) 比 \(n\) 要小得多
    • 内存限制：矩阵 \(Q_k\) 过大，限制步数 \(k\)

重启 GMRES

  • k 步迭代后没能足够趋近解，而继续操作可能收到内存限制（\(Q_k\) 太大），重启算法
  • 让现在的 \(x_k\) 作为 \(x_0\) 重启算法

4.2 预条件 GMRES

  • 非对称线性方程组：\(Ax=b\)
  • 加入预条件子：\(M^{-1}Ax=M^{-1}b\)

算法

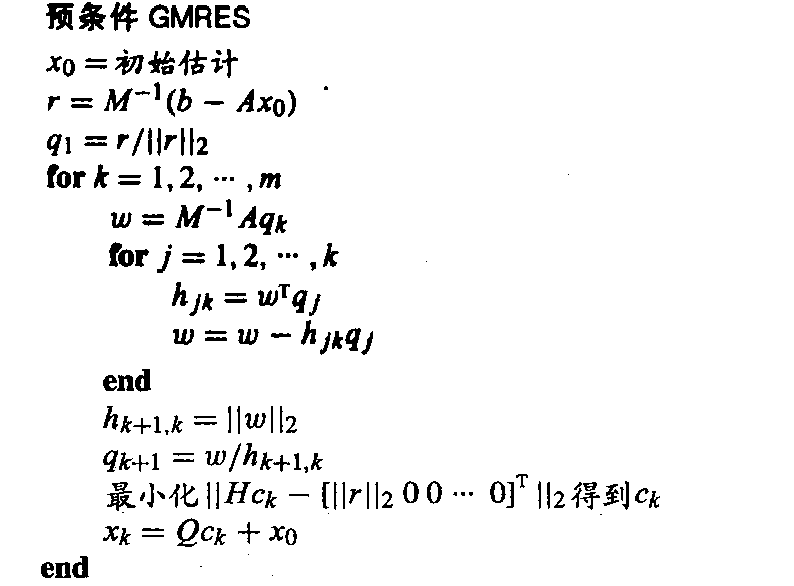
  • 注意到这些步骤都不需要对 \(M^{-1}\) 进行显式定义，\(M^{-1}\) 可以通过回代完成，其中假设 \(M\) 是一个简单或者分解的形式

\[ x=M^{-1}y\Leftrightarrow y=Mx \]

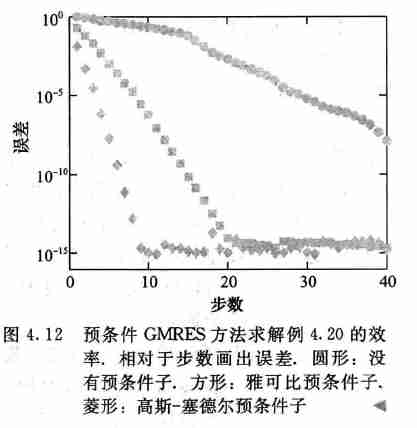
  • 实验

5. 非线性最小二乘

  • 线性方程组 \(Ax=b\) 的最小二乘解求解方法
    • 法线方程
    • QR 分解
  • 非线性方程组？高斯牛顿方法！

5.1 高斯牛顿方法

  • \(m\) 个方程，\(n\) 个未知变量的方程组

\[ \begin{array}{c} r_1(x_1,\cdots,x_n)=0\\ \cdots\\ r_m(x_1,\cdots,x_n)=0\\ \end{array} \]

  • 误差平方和
    • \(\dfrac{1}{2}\) 是为了简化后面模型

\[ E(x_1,\cdots,x_n)=\dfrac{1}{2}(r_1^2,\cdots,r_n^2)=\dfrac{1}{2}r^Tr \]

  • 最小化 \(E\)，让梯度 \(F(x)=\nabla{E(x)}=0\)

\[ F(x)=\nabla\left(\dfrac{1}{2}r^{T}(x)r(x)\right)=r^{T}(x)Dr(x) \]

  • 现在我们需要使用多变量的牛顿法求解非线性方程组 \(F^{T}(x)=0\)

\[ F^{T}=(Dr)^{T}r \]

\[ D\big(F^{T}\big)=D\big((Dr)^{T}r\big)=(Dr)^{T}Dr+\sum_{i=1}^{m}r_iDc_i \]

  • \(D\) 表示雅各比矩阵

\[ Dr=\begin{pmatrix} \dfrac{\partial{r_1}}{\partial{x_1}}&\cdots&\dfrac{\partial{r_1}}{\partial{x_n}}\\ \vdots&&\vdots\\ \dfrac{\partial{r_n}}{\partial{x_1}}&\cdots&\dfrac{\partial{r_n}}{\partial{x_n}}\\ \end{pmatrix} \]

  • \(c_i\) 是 \(Dr\) 的第 \(i\) 列，\(Dc_i=Hr_i\)，\(H\) 表示海森矩阵

\[ Hr_i=\begin{pmatrix} \dfrac{\partial^2{r_i}}{\partial{x_1}\partial{x_1}}&\cdots&\dfrac{\partial^2{r_i}}{\partial{x_1}\partial{x_n}}\\ \vdots&&\vdots\\ \dfrac{\partial^2{r_i}}{\partial{x_n}\partial{x_1}}&\cdots&\dfrac{\partial^2{r_i}}{\partial{x_n}\partial{x_n}}\\ \end{pmatrix} \]

  • 简化方法舍去 \(m\) 步求和
  • 本质上就是多便来给你牛顿法求解 \(F^{T}(x)=0\)

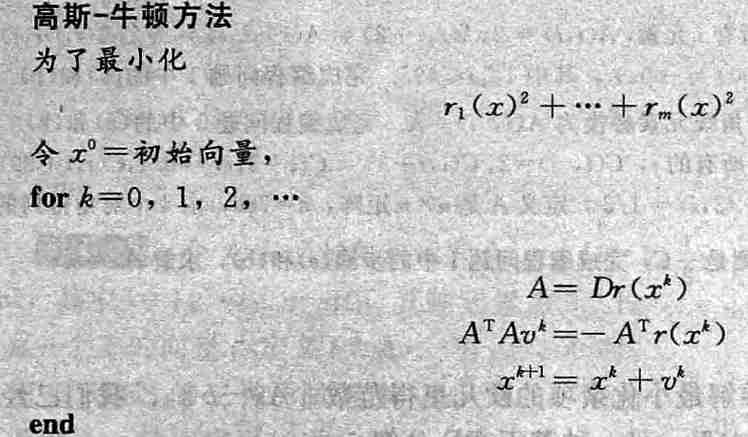
例题

  • 平面上 3 个圆，求交点
(1) 最小二乘：高斯牛顿法
  • 定义误差项

\[ \begin{array}{c} r_1(x,y)=\sqrt{(x-x_1)^2+(y-y_1)^2}-R_1\\ r_2(x,y)=\sqrt{(x-x_2)^2+(y-y_2)^2}-R_2\\ r_3(x,y)=\sqrt{(x-x_3)^2+(y-y_3)^2}-R_3\\ \end{array} \]

  • 应用上述算法

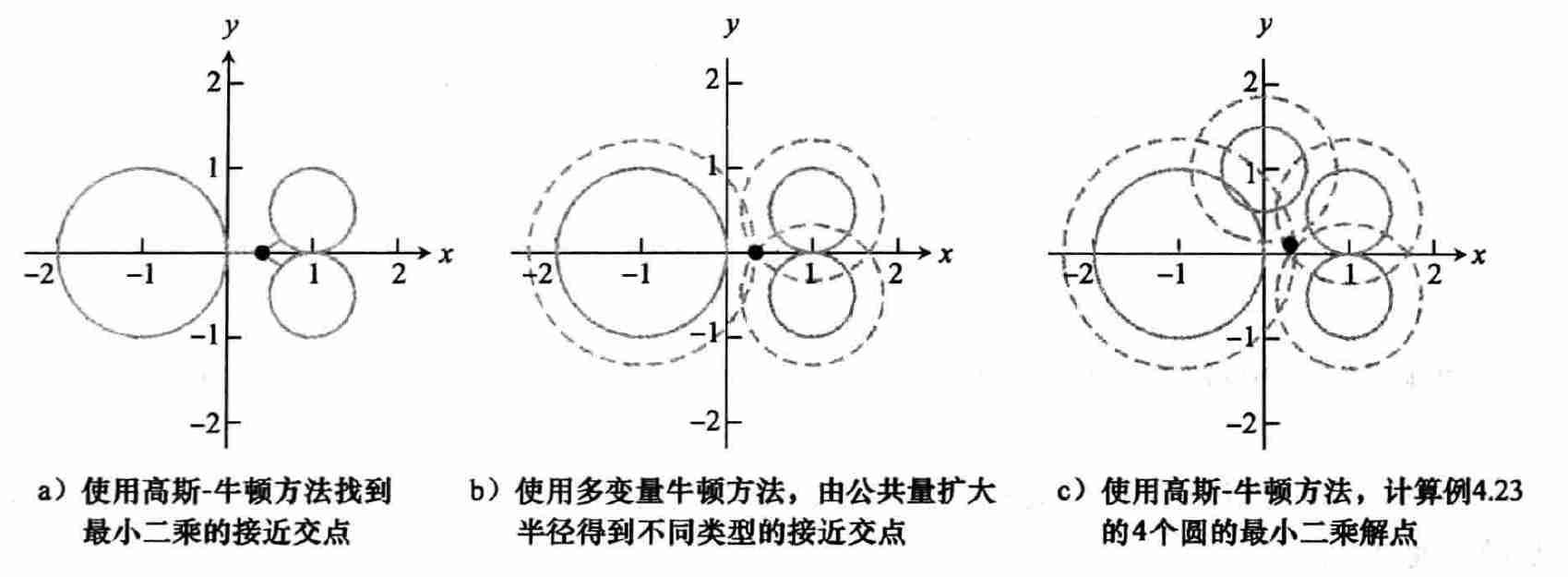
(2) 多变量牛顿方法
  • 不直接去寻找交点，我们可以使用公共量扩大（或者缩小）圆的半径，直到它们具有一个公共的交点，这等价于求解系统

\[ \begin{array}{c} r_1(x,y,K)=\sqrt{(x-x_1)^2+(y-y_1)^2}-(R_1+K)=0\\ r_2(x,y,K)=\sqrt{(x-x_2)^2+(y-y_2)^2}-(R_2+K)=0\\ r_3(x,y,K)=\sqrt{(x-x_3)^2+(y-y_3)^2}-(R_3+K)=0\\ \end{array} \]

  • 多变量牛顿方法求解
(3) 结合两种角度
  • 但是和上面不是一个题目了

  • 高斯牛顿，最小二乘

\[ \begin{array}{c} r_1(x,y,K)=\sqrt{(x-x_1)^2+(y-y_1)^2}-K=0\\ r_2(x,y,K)=\sqrt{(x-x_2)^2+(y-y_2)^2}-K=0\\ r_3(x,y,K)=\sqrt{(x-x_3)^2+(y-y_3)^2}-K=0\\ r_4(x,y,K)=\sqrt{(x-x_4)^2+(y-y_4)^2}-K=0\\ \end{array} \]

5.2 具有非线性参数的模型

  • 例如：拟合函数 \(y_i=f_i(t)=c_1t_1^{c_2}\)
  • 无法写成矩阵形式，而使用线性化则破坏了原有的最小二乘的定义
  • 可以使用高斯牛顿方法求解
  • 问题：收敛问题
    • 最小二乘问题中的非线性带来额外的挑战。法线方程以及 QR 方法只要系数矩阵 A 满秩都可以找到唯一解
    • 而对于非线性问题的高斯-牛顿迭代可能收敛到多个极小平方误差中的一个，尽可能使用初始向量的合理近似，有助于收敛到绝对极小

5.3 Levenberg-Marquardt 方法

  • 当最小二乘系数矩阵变为病态时将会面临挑战。例如使用法线方程最小二乘求解 \(Ax=b\) 时会遇到大的误差，这是由于 \(A^TA\) 具有大的条件数
  • 对于非线性最小二乘问题，情况通常会变得更糟。很多定义得很好的模型得到了条件数很差的 \(Dr\) 矩阵
    • Levenberg-Marquardt 方法使用 “正则化项” 部分修复这个问题
      • 可以看做是混合高斯-牛顿以及最速下降方法
  • Levenberg-Marquardt 方法是高斯牛顿方法的简单改进

  • \(\lambda\ne0\) 时，加强了矩阵 \(A^{T}A\) 对角元素的作用，通常可以改善条件数
    • 可以允许更宽的初始估计并实现收敛
  • 发展历程
    • 这个方法最初由 Levenberg[1944] 提出，在高斯-牛顿方法的 \(A^TA\) 加入 \(\lambda I\) 以改进对应的条件。几年后，DuPont 的一位统计学家 D. Marquardt，改进了Levenberg 的提议，将单位矩阵替换为 \(A^TA\) 的对角线矩阵（Mar-quardt[1963]）
  • 系数 \(\lambda\)
    • 尽管为了简单，我们将 \(\lambda\) 看做常数，但是该方法常常使用不同 \(\lambda\) 以适应问题，一般的策略是在每个迭代步骤中，只要余下的平方误差和在每步中降低就使用因子10连续降低 \(\lambda\)，如果误差升高，则拒绝当前步，并以因子10升高 \(\lambda\)