计算方法B.裴玉茹.05.最小二乘

• 数值分析课本第 4 章（最小二乘） + PPT（最小二乘法）

最小二乘

1. 最小二乘法线方程

• 动机
  • \(Ax=b\) 解不存在
  • 存在不一致的方程
  • 方程个数大于未知数个数
    • 超定方程
• \(\to\) 使用最小二乘

1.1 不一致的方程组

\[ \left\{ \begin{array}{c} x_1+x_2=2\\ x_1-x_2=1\\ x_1+x_2=3\\ \end{array} \right. \]

• 显然上面方程组是无解的 \(\to\) 不一致的
• 最小二乘
  • 与解最相似的向量 \(x\)
  • 欧式距离相近
• 上面的方程等价于求向量 \(x\) 满足

\[ {x_1}\begin{bmatrix}1\\1\\1\\\end{bmatrix} +{x_2}\begin{bmatrix}1\\-1\\1\\\end{bmatrix} =\begin{bmatrix}2\\1\\3\\\end{bmatrix} \]

\[ \begin{array}{c} {x_1}v_1+{x_2}v_2=b\\ [v_1,v_2][x_1,x_2]^{T}=b\Leftrightarrow Ax=b\\ \end{array} \]

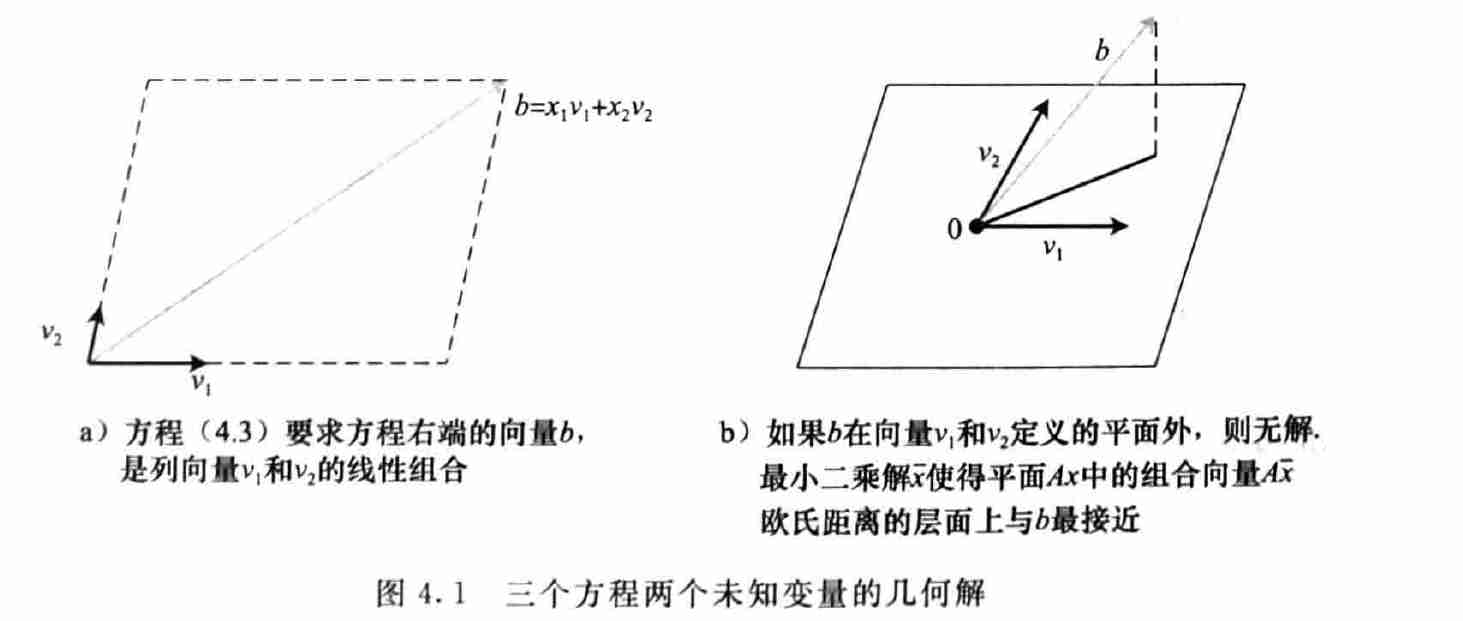
• 三个向量共面才有解
• 最小二乘：
  • \(b\) 在 \(v_1,v_2\) 张成平面的投影记作 \(b'\)
  • 近似解 \(\bar{x}\) 满足：\(v_1\bar{x}_1+v_2\bar{x}_2=b'\)

• 近似解满足
  • 向量 \(b-A\bar{x}\) 和平面 \(\{Ax|x\in\mathbb{R}^{n}\}\) 垂直
• 转置
  • \((A+B)^{T}=A^{T}+B^{T}\)
  • \((AB)^{T}=B^{T}A^{T}\)
• 正交
  • 最小二乘基于正交，从一点到一个平面的最短距离，由一个到平面的正交线段表示，法线方程可以确定该线段，这表示最小二乘的误差
• 向量垂直（正交）：内积为 0
• 那么我们可以得到近似解的性质
  • 对于任意 \(x\in\mathbb{R}^{n}\)，有 \((Ax)^{T}(b-A\bar{x})=0\) 成立

\[ x^{T}A^{T}(b-A\bar{x})=0,\forall x\in\mathbb{R}^n \]

• 那么我们得到，\(n\) 维向量 \(A^{T}(b-A\bar{x})\) 和任意 \(n\) 维向量垂直（包括自身），于是有

\[ A^{T}(b-A\bar{x})=0 \]

• 最小二乘的解满足如下方程（也被称为法线方程）

\[ A^{T}A\bar{x}=A^{T}b \]

• 最小二乘的解能够最小化余项 \(r=b-Ax\) 的欧式长度

余项表示

• 欧式长度（2 范数）

\[ \Vert{r}\Vert_{2}=\sqrt{r_1^2+\cdots+r_{n}^2} \]

• 平方误差

\[ SE=\Vert{r}\Vert_2^2 \]

• 平均平方根误差

\[ RMSE=\sqrt{\frac{SE}{m}} \]

• 是等价度量

1.2 数据的拟合模型

最小二乘数据拟合

• 最小二乘是数据压缩的经典例子
• 条件数

• 用 Eigen 库写了一下，感觉确实有些难顶，基本不是正常值
  • c++代码

2. 模型概述

• 数据建模包含不同的模型
  • 底层物理规律
  • 经验公式
  • ...

2.1 周期数据

• 周期数据使用周期模型
• 一日气温变化

\[ u=c_1+c_2\cos(2\pi t)+c_2\sin(2\pi t),\qquad t=\dfrac{24小时表示的时间}{24} \]

• 对于特定的基函数， 最小二乘问题可以大大简化
  • 上述选择方式使得法线方程已经是对角线形式
• 可以增加阶数，添加项 \(c_3\cos(4\pi t)\)

2.2 数据线性化

指数模型

\[ y=c_1e^{c_2t} \]

• 非线性模型：系数不是线性的
  • 方法1：非线性最小二乘问题
  • 方法2：“线性化”
• 线性化

\[ \ln{y}=\ln{c_1}+c_2t=k+c_2t \]

• 求出 \(k,c_2\) 之后在求得 \(c_1,c_2\)

评价标准改变

• 实际上改变了评价标准
• 原来的评价标准：最小化如下式子

\[ \sum_{i=1}^{n}(c_1e^{c_2t_i}-y_i)^2 \]

• 线性化之后的评价标准：最小化如下式子

\[ \sum_{i=1}^{n}(\ln{c_1}+c_2t_i-\ln{y_i})^2 \]

• 具体使用哪一种形式，需要用户确定更需要最小化哪种误差，是原始意义的误差

幂法则模型

\[ y=c_1t^{c_2} \]

• 线性化

\[ \ln{y}=\ln{c_1}+c_2\ln{t}=k+c_2\ln{t_2} \]

• 实际例子
  • 半衰期：\(y=c_1te^{c_2t}\Rightarrow \ln{y}-\ln{t}=\ln{c_1}+c_2t\)

3. QR 分解

3.1 格拉姆-施密特正交与最小二乘

• 格拉姆-施密特方法是对一组向量正交化
  • 给定一组输人的 \(m\) 维向量，目的是找出正交坐标系统，获取由这些向量张成的空间，
  • 更精确地讲，给定 \(n\) 个线性无关的输人向量，该方法计算 \(n\) 个彼此垂直的单位向量，张成和输入向量相同的子空间，单位长度由欧几里得（即 2 范数）进行定义
• 输入为 \(\mathbb{R}^m\) 中的 \(n\) 个线性无关向量 \(A_1,\cdots,A_n\)（\(n\le m\)）

思路

• 定义问题为 \(P(n)\)
• 去除其中的一个向量 \(A_1\)，作为最后生成的正交向量组中的一个向量
• 剩余向量做如下操作：\(A_i=A_i-(A_i\cdot \dfrac{A_1}{\Vert{A_1}\Vert})\dfrac{A_1}{\Vert{A_1}\Vert}\)
  • 减去 \(A_1\) 方向上的分量
• 此时剩余的向量与 \(A_1\) 都垂直，问题转化为剩余向量的 \(P(n-1)\) 问题

算法流程

• 初始化

\[ y_1=A_1,q_1=\dfrac{y_1}{\Vert{y_1}\Vert_2} \]

• 第 \(2\) 个向量

\[ y_2=A_2-q_1(q_1^{T}A_2),q_2=\dfrac{y_2}{\Vert{y_2}\Vert_2} \]

• \(\cdots\)
• 第 \(i\) 个向量
  • 第二数学归纳法可以证明 \(q_i\) 和之前的向量 \(q_j/y_j\) 正交

\[ y_i=A_i-q_1(q_1^{T}A_i)-\cdots-q_{i-1}(q_{i-1}^{T}A_{i}),q_i=\dfrac{y_i}{\Vert{y_i}\Vert_2} \]

• \(\cdots\)
• 第 \(n\) 个向量

矩阵形式

• 矩阵 \(R\)
• \(r_{ii}=\Vert{y_i}\Vert_2\)
• \(r_{i,j}=q_i^{T}A_j,(i\le j)\)
• \(r_{i,j}=0,(i>j)\)
• 我们能够得到如下式子
  • \(A_j\) 在各个正交向量上的投影之和

\[ A_j=r_{1,j}q_1+\cdots+r_{j-1,j}q_{j-1}+r_{j,j}q_j \]

• 矩阵形式如下

\[ \begin{pmatrix}A_1\cdots A_n\end{pmatrix} =\begin{pmatrix}q_1\cdots q_n\end{pmatrix}R =\begin{pmatrix}q_1\cdots q_n\end{pmatrix} \begin{bmatrix} r_{11}&r_{12}&\cdots&r_{1n}\\ &r_{22}&\cdots&r_{2n}\\ &&\ddots&\vdots\\ &&&r_{nn} \end{bmatrix} \]

• 简记为 \(A=QR\)，称为消减 QR 分解
• 如果 \(A_j\) 线性无关，则主对角元全都非零
• 如果 \(A_j\) 在 \(A_1,\cdots,A_{j-1}\) 章程的线性空间中，那么 \(r_{jj}=0\)
• 如上的方法，我们称为是经典的格拉姆-施密特正交算法
• 总结

QR 分解的应用

• 求解 \(n\) 个方程 \(n\) 个未知数的系统 \(Ax=b\)
• 最小二乘
• 特征值计算

求解方程

• 假设 \(A\) 是非奇异矩阵
  • \(Ax=b\Rightarrow QRx=b\Rightarrow Rx=Q^{T}b\)
    • \(Q\) 是正交矩阵，\(Q^{T}=Q^{-1}\)
    • \(R\) 是上三角矩阵
  • 复杂度约为 \(LU\) 的 3 倍
    • 大概：\(n^3\) 乘法 + \(n^3\) 加法
      • 感觉次数不太对，好像没把归一化的次数算上

最小二乘

• 正交变换不改变向量的 2 范数

\[ \Vert{Ax}\Vert_2=(Ax)^{T}(Ax)=x^{T}A^{T}Ax=x^{T}(A^{T}A)x=x^{T}x=\Vert{x}\Vert_2 \]

• 那么我们可以推导得到，如果 \(A\) 是正交矩阵，\(\Vert{AB}\Vert_2=\Vert{B}\Vert_2\)

\[ \Vert{AB}\Vert_2=\max_{\Vert{x}\Vert_2\ne0}\dfrac{\Vert{ABx}\Vert_2}{\Vert{x}\Vert_2}=\max_{\Vert{x}\Vert_2\ne0}\dfrac{\Vert{Bx}\Vert_2}{\Vert{x}\Vert_2}=\Vert{B}\Vert_2 \]

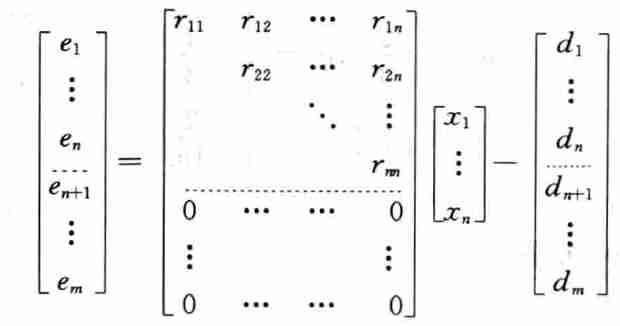
• \(A\) 为 \(m\times n\) 矩阵（\(m\ge n\)）

\[ \Vert{Ax-b}\Vert_2=\Vert{QRx-b}\Vert_2=\Vert{Rx-Q^{T}b}\Vert_2=\Vert{Rx-d}\Vert_2=\Vert{e}\Vert_2 \]

• 假定 \(r_{ii}\ne0\)，\(A\) 满秩，那么有如下矩阵形式

• 于是最小二乘误差：

\[ \Vert{e}\Vert_2=\sqrt{\sum_{i=n+1}^{m}d_{n+1}^{2}} \]

• 方程的最小二乘解：通过方程组回代即可计算得到 \(x\)

3.2 改进的格拉姆-施密特正交

• 微小改进可以在机器计算中改进精度，与原始方法在数学上等价

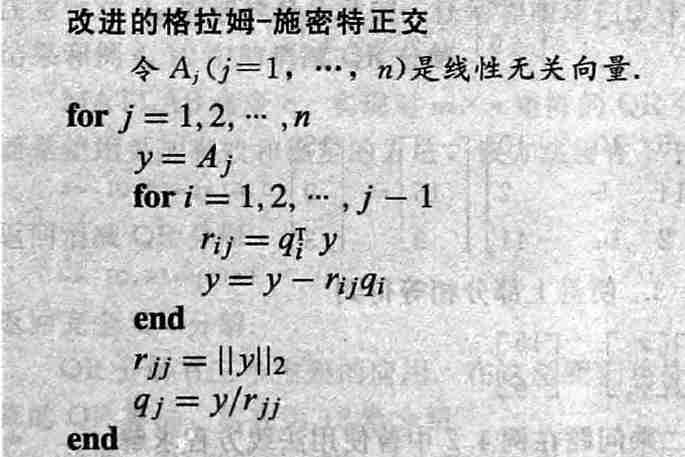
• 因为在第 \(i\) 步的时候，\(A_j\) 中已经不含有 \(q_1,\cdots,q_{i-1}\) 的成分了（都已经减去了），因此只需要做余项的投影
• 更加稳定
  • 直观上讲，减少了 \(q_1,\cdots,q_{i-1}\) 成分计算带来的误差

3.3 豪斯霍尔德反射子

• 相较改进的格拉姆-施密特正交化方法
  • 更少的计算
  • 舍入误差的角度而言，更加稳定
• 豪斯霍尔德反射子是正交矩阵，通过 \(m-1\) 维平面反射 \(m\) 维向量
  • 每个向量乘上矩阵之后，长度不变
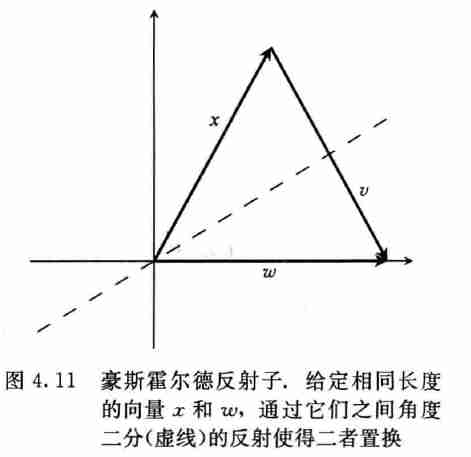
• 给定一个向量 \(x\)，我们要重新找出一个相同长度的向量 \(w\)，计算豪斯霍尔德反射得出矩阵 \(H\) 满足 \(Hx=w\)
• 原始方法
  • 画出 \(m-1\) 维平面二分 \(x\) 和 \(w\)，并连接他们的向量垂直，并且通过该平面反射所有向量

投影矩阵

• \(\Vert{x}\Vert_2=\Vert{w}\Vert_2\Rightarrow(w-x)^{T}(w+x)=0\)
  • 正交
• 定义 \(v=w-x\)，投影矩阵 \(P=\dfrac{vv^{T}}{v^{T}v}\)
• 投影矩阵满足 \(P^{2}=P\)

\[ P^{2}=\dfrac{vv^{T}vv^{T}}{(v^{T}v)^2}=\dfrac{v(v^{T}v)v^{T}}{(v^{T}v)^2}=\dfrac{(v^{T}v)vv^{T}}{(v^{T}v)^2}=\dfrac{vv^{T}}{v^{T}v}=P \]

• 上述 \(P\)
  • 对称投影矩阵
    • 证明 \(P^{T}=P\) 即可
  • \(Pv=v\)
  • 对于任意向量 \(u\)，\(Pu\) 是 \(u\) 在 \(v\) 上的投影
    • 投影定义即证

豪斯霍尔德反射子

• 如上图，\(x-2Px=w\)
• 定义 \(H=I-2P\)
  • \(Pv=v\)
  • \(v^{T}(x+v)=(x-v)^{T}(x+v)=0\)

\[ \begin{aligned} Hx&=Ix-2Px=x-2Px\\ &=w-v-\dfrac{2vv^{T}x}{v^{T}v}\\ &=w-Pv-\dfrac{2vv^{T}x}{v^{T}v}\\ &=w-\dfrac{vv^{T}v+vv^{T}x+vv^{T}(w-v)}{v^{T}v}\\ &=w-\dfrac{vv^{T}(x+v)}{v^{T}v}\\ &=w-\dfrac{vv^{T}(x+v)}{v^{T}v}\\ &=w\\ \end{aligned} \]

• \(H\) 即为豪斯霍尔德反射子
• \(H\) 是对称的
  • \(I,P\) 都是对称的
• \(H\) 是正交的

\[ H^{T}H=HH=(I-2P)(I-2P)=I-4P+4P^2=I \]

QR 分解

• 计算代价，\(n\times n\) 矩阵
  • 乘法：\(\dfrac{2}{3}n^{3}\)
  • 加法：\(\dfrac{2}{3}n^{3}\)
  • 怎么算出来的，这么低？没搞懂