计算方法B.裴玉茹.04.插值(3)

• 数值分析课本第 3 章（插值） + PPT（多项式插值）

插值

• PPT 补充

1. 多项式

Weierstrass 近似定理

• 假设函数 \(f\) 是 \([a,b]\) 区间上的连续函数，对于 \(\epsilon>0\)，存在多项式 \(P(x)\) 使得对于 \([a,b]\) 区间上任意的 \(x\)，\(\vert{f(x)-p(x)}\vert<\epsilon\)

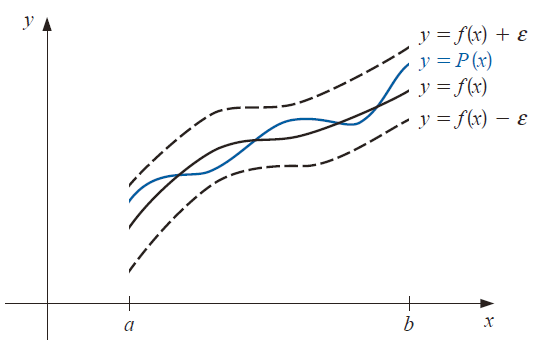
• 维尔斯特拉斯定理给出多项式的近似误差界
• 讨论了近似多项式的存在性

泰勒多项式

• 可以给出连续可导函数在某点附近的一个近似多项式
  • 泰勒多项式与给定函数在某一特定点上尽可能一致，但它们仅在该点附近保证精度

\[ f(x)=\sum_{k=0}^{n}\dfrac{f^{(k)}(x_0)}{k!}(x-x_0)^k+\dfrac{f^{(n+1)}(\xi(x_0))}{(n+1)!}(x-x_0)^{n+1} \]

• 近似多项式 + 截断误差

2. 拉格朗日多项式

插值多项式

• 插值多项式具体形式见前面的 note
• 这里一共 \(n+1\) 个点，\((x_i,f(x_i)),i=0,\cdots,n+1\)

\[ p(x)=\sum_{k=1}^{n}f(x_k)L_{n,k}(x) \]

余项

\[ f(x)=p(x)+{\color{blue}\dfrac{f^{(n+1)}(\xi(x))}{(n+1)!}(x-x_0)(x-x_1)\cdots(x-x_n)} \]

• 证明：note
• 形式简单，实际操作计算困难，\(f^{(n+1)},\xi(x)\)
• 内插与外推
  • 从误差多项式看，内插比外推更准确
• 一般来说，误差随着阶数的增加而减小，误差分布在所有给定节点上
  • 分母：\((n+1)!\)

荣格现象

• 插值次数越高，插值结果越偏离原函数的现象称为龙格现象
• 荣格函数 \(\dfrac{1}{1+25x^2}\)
  • 对于 \(n\) 阶的插值多项式,在区间的端点附近出现了震荡
  • 原始函数f，5阶插值多项式，9阶插值多项式

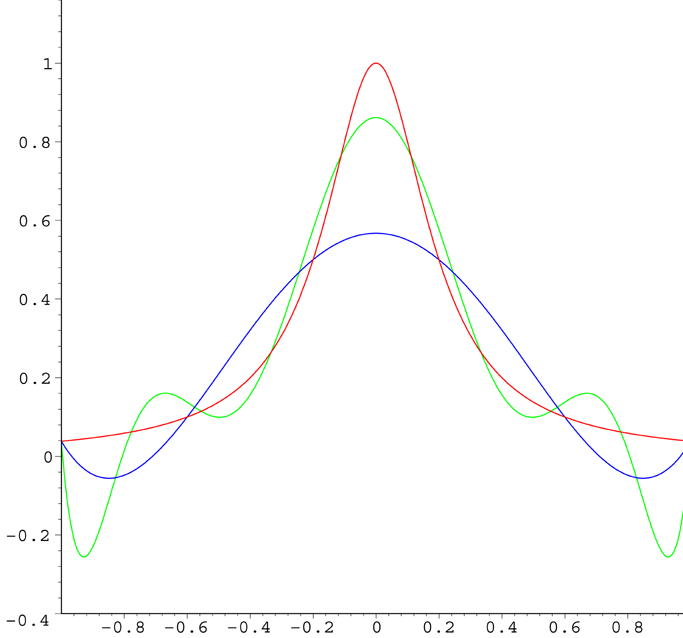
• 原因：对于荣格函数，其高阶导数在区间端点数值急剧上升

重用低阶拉格朗日多项式

• \(k\) - 点拉格朗日多项式
  • \(k\) 个整数 \(m_1,m_2,\cdots,m_k\)，\(0\le m_i\le n\)
  • \(P_{m_1,\cdots,m_k}(x)\) 表示定义在 \(k\) 点 \(x_{m_1},\cdots,x_{m_k}\) 的多项式
• 使用低阶的拉格朗日多项式生成高阶的多项式

递推公式：Neville's 方法

• 函数 \(f\) 定义在 \(k+1\) 个节点 \(x_0,\cdots,x_{k}\) 上
• \(k\) 阶拉格朗日多项式 \(P(x)\)
• \(i\ne j\)

\[ P(x)=\dfrac{(x-x_j)P_{0,1,\cdots,j-1,j+1,\cdots,k}(x)-(x-x_i)P_{0,1,\cdots,i-1,i+1,\cdots,k}}{x_i-x_j} \]

递推公式证明

• \(r\ne i,j\)

\[ P(x_r)=\dfrac{f(x_r)(x_r-x_j)-f(x_r)(x_r-x_i)}{(x_i-x_j)}=f(x_r) \]

• \(r=i\)

\[ P(x_r)=P(x_i)=\dfrac{(x_i-x_j)f(x_i)}{(x_i-x_j)}=f(x_i) \]

• \(r=j\) 同理

使用递推公式

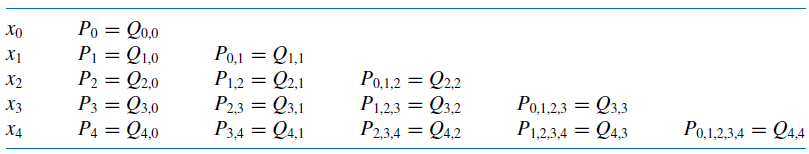
3. 牛顿差分多项式

差商

• 0 阶差商

\[ f[x_i]=f(x_i) \]

• 1 阶差商

\[ f[x_i,x_{i+1}]=\dfrac{f[x_{i+1}]-f[x_i]}{x_{i+1}-x_i} \]

• 2 阶差商

\[ f[x_i,x_{i+1},x_{i+2}]=\dfrac{f[x_{i+1},x_{i+2}]-f[x_i,x_{i+1}]}{x_{i+2}-x_i} \]

• k 阶差商

\[ f[x_i,\cdots,x_{i+k}]=\dfrac{f[x_{i+1},\cdots,x_{i+k}]-f[x_i,\cdots,x_{i+k-1}]}{x_{i+k}-x_i} \]

n 阶牛顿前向差分多项式

• \(n+1\) 点插值

\[ P_n(x)=f[x_0]+\sum_{k=1}^{n}f[x_0,\cdots,x_k](x-x_0)\cdots(x-x_{k-1}) \]

前向差分与后向差分

• 等间距公式

\[ x_i=x_0+ih,\qquad(i=0,\cdots,n) \]

• 前向差分

\[ \begin{array}{c} \Delta{f_i}=f_{i+1}-f_i\\ \Delta^{k}{f_i}=\Delta^{k-1}(\Delta{f_i})=\Delta^{k-1}f_{i+1}-\Delta^{k-1}f_i \end{array} \]

• 后向差分

\[ \begin{array}{c} \nabla{f_i}=f_{i+1}-f_i\\ \nabla^{k}{f_i}=\nabla^{k-1}(\nabla{f_i})=\nabla^{k-1}f_{i+1}-\nabla^{k-1}f_i \end{array} \]

牛顿前向差分与后向差分

前向差分

• 等间距

\[ x_i=x_0+ih \]

• \(x\) 的另一种表示

\[ x=x_0+th \]

• 差分公式

\[ \begin{aligned} P_n(x)&=f[x_0]+\sum_{k=1}^{n}f[x_0,\cdots,x_k](x-x_0)\cdots(x-x_{k-1})\\ P_n(x)=P_n(x_0+th)&=f[x_0]+\sum_{k=1}^{n}\dfrac{\Delta^{k}f(x_0)}{k!h^{k}}t(t-1)\cdots(t-k+1)h^{k}\\ &=f[x_0]+\sum_{k=1}^{n}\dfrac{\Delta^{k}f(x_0)}{k!h^{k}}{t \choose k}k!h^{k}\\ &=f[x_0]+\sum_{k=1}^{n}{t \choose k}\Delta^{k}f(x_0)\\ &=\sum_{k=0}^{n}{t \choose k}\Delta^{k}f(x_0)\\ \end{aligned} \]

• 误差

\[ \begin{aligned} R_{n}(x)&=\dfrac{f^{(n+1)}(\xi(x))}{(n+1)!}(x-x_0)(x-x_1)\cdots(x-x_n)\\ &=\dfrac{f^{(n+1)}(\xi(x))}{(n+1)!}t(t-1)\cdots(t-n)h^{n+1},\quad\xi(x)\in[x_0,x_n]\\ \end{aligned} \]

后向差分

• 类似的有如下式子

• 等间距

\[ x_i=x_0+ih=x_n-(n-i)h \]

• \(x\) 的另一种表示

\[ x=x_n+th \]

• 差分公式

\[ \begin{aligned} P_n(x)&=f[x_n]+\sum_{k=1}^{n}f[x_{n},\cdots,x_{n-k}](x-x_{n})\cdots(x-x_{n-k+1})\\ P_n(x)=P_n(x_0+th)&=f[x_n]+\sum_{k=1}^{n}\dfrac{\nabla^{k}f(x_0)}{k!h^{k}}t(t+1)\cdots(t+k-1)h^{k}\\ &=f[x_n]+\sum_{k=1}^{n}\dfrac{\nabla^{k}f(x_0)}{k!h^{k}}(-1)^{k}(-t)(-t-1)\cdots(-t-k+1)h^{k}\\ &=f[x_n]+\sum_{k=1}^{n}\dfrac{\nabla^{k}f(x_0)}{k!h^{k}}(-1)^{k}{-t \choose k}k!h^{k}\\ &=f[x_n]+\sum_{k=1}^{n}(-1)^{k}{-t \choose k}\nabla^{k}f(x_0)\\ &=\sum_{k=0}^{n}(-1)^{k}{-t \choose k}\nabla^{k}f(x_0)\\ \end{aligned} \]

• 误差（一样）

\[ \begin{aligned} R_{n}(x)&=\dfrac{f^{(n+1)}(\xi(x))}{(n+1)!}(x-x_0)(x-x_1)\cdots(x-x_n)\\ &=\dfrac{f^{(n+1)}(\xi(x))}{(n+1)!}t(t-1)\cdots(t-n)h^{n+1},\quad\xi(x)\in[x_0,x_n]\\ \end{aligned} \]

选择

• 在计算机中存在机器精度的问题，针对不同位置的数据，我们会选择使用前向差分还是后向差分
  • 估计数据离 \(x_0\) 更近：前向差分
  • 估计数据离 \(x_n\) 更近：后向差分

4. 厄米特多项式

• 厄米特插值多项式 \(\psi\)
  • 多项式与函数在 \(n+1\) 个节点上一致
  • 切线方向也一致

\[ \begin{array}{c} \psi(x_i)=f(x_i)\\ \psi'(x_i)=f'(x_i)\\ \end{array} \]

定理

• 如果函数 \(f\) 是连续函数 \(f\in C[a,b]\)，\(x_1,\cdots,x_n\in[a,b]\)，在节点 \(x_1,\cdots,x_n\) 满足 \(f\) 与 \(f'\) 的至多 \(2n+1\) 阶厄米特多项式定义如下

\[ H_{2n+1}(x)=\sum_{j=0}^{n}f(x_j)H_{n,j}(x)+\sum_{j=1}^{n}f'(x_j)\hat{H}_{n,j}(x) \]

• 其中

\[ \begin{array}{c} H_{n,j}(x)=[1-2(x-x_j)L'_{n,j}(x_j)]L^{2}_{n,j}(x)\\ \hat{H}_{n,j}(x)=(x-x_j)L^{2}_{n,j}(x) \end{array} \]

• 若 \(f\in C^{2n+2}[a,b]\)，则余项

\[ f(x)-H_{2n+1}(x)=\dfrac{(x-x_0)^2\cdots(x-x_n)^2}{(2n+2)!}f^{(2n+2)}(\xi) \]

定理证明

值相等

• 对于 \(n\) 阶拉格朗日多项式

\[ L_{n,j}(x_i)= \left\{\begin{array}{c} 0,&\mathrm{if}\ i\ne j\\ 1,&\mathrm{if}\ i=j\\ \end{array}\right. \]

• 于是有

\[ H_{n,j}(x_i)= \left\{\begin{array}{c} 0,&\mathrm{if}\ i\ne j\\ 1,&\mathrm{if}\ i=j\\ \end{array}\right. \]

\[ \hat{H}_{n,j}(x_i)= \left\{\begin{array}{c} 0,&\mathrm{if}\ i\ne j\\ 0,&\mathrm{if}\ i=j\\ \end{array}\right. \]

• 那么我们能够得到

\[ H_{2n+1}(x_i)=\sum_{j=0}^{n}f(x_j)H_{n,j}(x_i)+\sum_{j=1}^{n}f'(x_j)\hat{H}_{n,j}(x_i)=f(x_i) \]

一阶导相等

• 分析

\[ \begin{array}{c} H'_{n,j}(x)=2[1-2(x-x_j)L'_{n,j}(x_j)]L_{n,j}(x)L'_{n,j}(x)-2L'_{n,j}(x_j)L^2_{n,j}(x)\\ \hat{H}'_{n,j}(x)=2(x-x_j)L_{n,j}(x)L'_{n,j}(x)+L^2_{n,j}(x)\\ \end{array} \]

• 于是有

\[ H'_{n,j}(x_i)= \left\{\begin{array}{c} 0,&\mathrm{if}\ i\ne j\\ 0,&\mathrm{if}\ i=j\\ \end{array}\right. \]

\[ \hat{H}_{n,j}(x_i)= \left\{\begin{array}{c} 0,&\mathrm{if}\ i\ne j\\ 1,&\mathrm{if}\ i=j\\ \end{array}\right. \]

• 得到

\[ H'_{2n+1}(x_i)=\sum_{j=0}^{n}f(x_j)H'_{n,j}(x_i)+\sum_{j=1}^{n}f'(x_j)\hat{H}'_{n,j}(x_i)=f'(x_i) \]

计算问题

• 需要计算拉格朗日多项式及其导数
• 即便对于低阶厄米特多项式计算复杂

利用牛顿差分公式

• 利用牛顿差分多项式计算厄米特多项式

\[ H_{2n+1}(x)=f[z_0]+\sum_{k=1}^{n}f[z_0,\cdots,z_k](x-z_0)\cdots(x-z_{k-1}) \]

• \(2n+2\) 个节点

\[ z_{2i}=z_{2i+1}=x_i \]

• 复制节点对应的一阶差商的定义

\[ f[z_{2i},z_{2i+1}]=f'(z_{2i})=f'(x_i) \]

定理

• 假设 \(f\) 是 \(n\) 阶连续函数 \(f\in C^{n}[a,b]\)，\(x_0,\cdots,x_n\) 是 \([a,b]\) 区间中不同数，则 \([a,b]\) 区间中存在 \(\xi\) 使得

\[ f[x_0,\cdots,x_n]=\dfrac{f^{n}(\xi)}{n!} \]

• 证明：推广罗尔定理
  • \(g(x)=f(x)-P_n(x)\) 有 \(n+1\) 个过零点
  • \(g^{(n)}(\xi)=f^{(n)}(\xi)-n!f[x_0,\cdots,x_n]\)
• 于是我们可以得到复制节点的差商

\[ f[z_{2i},z_{2i+1}]=f'(\xi)=f'(z_{2i})=f'(x_i) \]

计算示例

5. 方法对比

6. 三次样条插值

• 分段多项式插值

分段线性插值

• \(C^{0}\) 连续
  • 缺乏在节点处对函数方向（高阶导数）的描述

三次样条

• 插值、连续、一阶导相等、二阶导相等
• 边界条件（两个选一个即可）
  • 自由或自然边界条件：\(S''(x_0)=S''(x_n)=0\)
  • 固支边界条件：\(S'(x_0)=f'(x_0),S'(x_n)=f'(x_n)\)

对比

	\(f\)	\(f'\)	\(f''\)
厄米特多项式 \(H(x)\)	相等	相等	未定义
三阶样条多项式 \(S(x)\)	相等	连续	连续

自然三次样条

• \(S''(x_0)=S''(x_n)=0\)
• note

固支三次样条

• \(S'(x_0)=f'(x_0),S'(x_n)=f'(x_n)\)
• note
  • 钳制三次样条的特殊情况
  • \(v_1=f'(x_0),v_2=f'(x_n)\)