计算方法B.裴玉茹.04.插值(2)
- 数值分析课本第 3 章(插值) + PPT(多项式插值)
插值
4. 三次样条
- 在多项式插值中,多项式给出的单一公式满足所有数据点
- 而样条则使用多个公式,其中每个都是低阶多项式,来通过所有数据点
- 线性样条:直接把相邻的点连起来
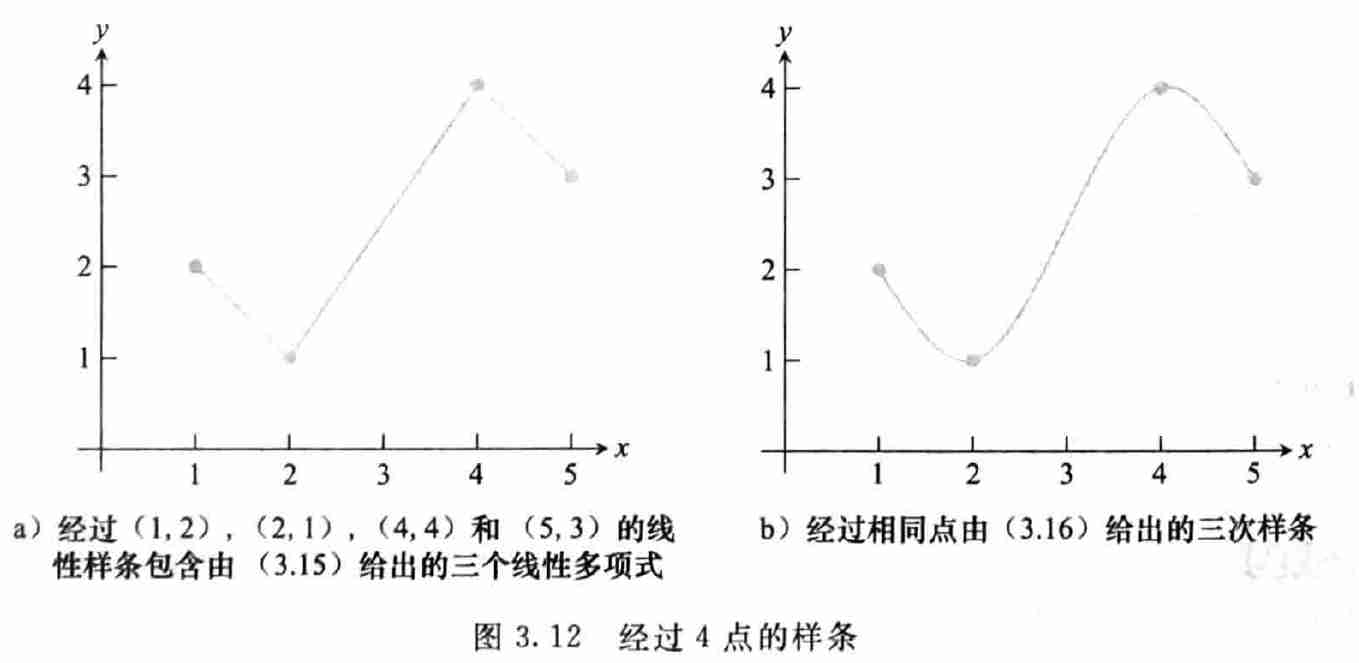
4.1 样条的性质
三次样条
- 给定 \(n\) 个点,\((x_1,y_1),\cdots,(x_n,y_n)\),其中 \(x_i\) 升序,通过点 \((x_1,y_1),\cdots,(x_n,y_n)\) 的三次样条 \(S(x)\) 是一组三次多项式
\[ \begin{array}{c} S_1(x)=y_1+b_1(x-x_1)+c_1(x-x_1)^2+d_1(x-x_1)^3,x\in[x_1,x_2]\\ S_2(x)=y_2+b_2(x-x_2)+c_2(x-x_2)^2+d_2(x-x_2)^3,x\in[x_2,x_3]\\ \cdots\\ S_{n-1}(x)=y_{n-1}+b_{n-1}(x-x_{n-1})+c_{n-1}(x-x_{n-1})^{2}+d_{n-1}(x-x_{n-1})^3,x\in[x_{n-1},x_n]\\ \end{array} \]
- 要求具备如下性质
\[ \begin{array}{l} S_i(x_i)=y_i,S_i(x_{i+1})=y_{i+1},i=1,\cdots,n-1\\ S_{i-1}'(x_i)=S_i'(x_i),i=2,\cdots,n-1\\ S_{i-1}''(x_i)=S_i''(x_i),i=2,\cdots,n-1\\ \end{array} \]
- 连接点:连续、斜率相同、曲率相同
- 求解参数
- 未知数:\(3(n-1)=3n-3\)
- 方程:\((n-1)+(n-2)+(n-2)=3n-5\)
- 因此存在无穷多的三次样条曲线
自然样条
- \(S''(x_1)=S''(x_n)=0\)
- 加上这个条件可以唯一解得三次样条
- 自然三次样条
- 可以添加其他边界条件形成其他样条曲线

- 引入记号
- \(\delta_i=x_{i+1}-x_i\)
- \(\Delta_i=y_{i+1}-y_i\)
- 引入额外未知变量 \(c_n=\dfrac{S_{n-1}''(x_n)}{2}\)
- 让下一行多了一个方程
- (3.21)
\[ \begin{array}{c} d_i=\dfrac{c_{i+1}-c_i}{3\delta_i}\\ i=1,\cdots,n-1\ \end{array} \]
- (3.19)
- 代入 \(d_i\)
\[ \begin{array}{c} b_i=\dfrac{\Delta_i}{\delta_i}-c_i\delta_i-d_i\delta_i^2=\dfrac{\Delta_i}{\delta_i}-\dfrac{\delta_i}{3}(2c_i+c_{i+1})\\ i=1,\cdots,n-1\ \end{array} \]
- (3.20)
- 代入 \(d_i,b_i\)
\[ \begin{array}{c} c_i\delta_i+c_{i+1}(2\delta_i+2\delta_{i+1})+c_{i+2}(2\delta_{i+1})=3\left(\dfrac{\Delta_{i+1}}{\delta_{i+1}}-\dfrac{\Delta_i}{\delta_i}\right)\\ i=1,\cdots,n-2 \end{array} \]
- 加上自然样条的限制
- 严格对角占优,有唯一解
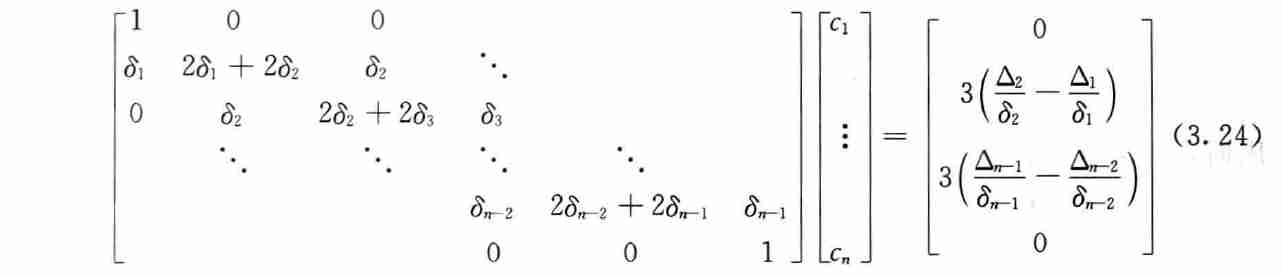
- 求解得到 \(c_i\),从而计算得到 \(b_i,d_i\)
自然三次样条

不同边界条件

- 不同效果如下
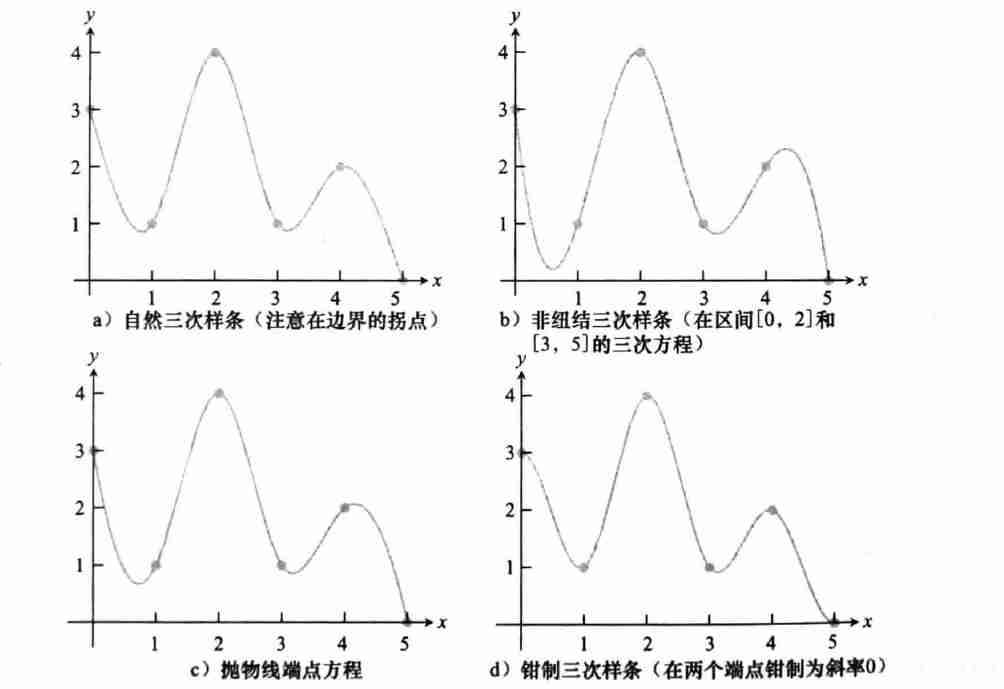
4.2 端点条件
曲率调整三次样条
- 端点曲率是两个用户设定值,而不是 \(0\)
\[ \begin{array}{c} S''(x_1)=v_1\\ S''(x_n)=v_2\\ \end{array} \]
- 矩阵中表现如下(还是严格对角占优)

钳制三次样条
- 端点的一阶导数为用户设定值
\[ \begin{array}{c} S'(x_1)=v_1\\ S'(x_n)=v_2\\ \end{array} \]
- 表示为
\[ \begin{array}{c} b_1=\dfrac{\Delta_1}{\delta_1}-\dfrac{\delta_1}{3}(2c_1+c_2)=v_1\\ b_{n-1}+2c_{n-1}\delta_{n-1}+3d_{n-1}\delta_{n-1}^2=v_2\\ \end{array} \]
- 转化为
\[ \begin{array}{c} c_1(2\delta_1)+c_2(\delta_1)=3(v_1-\dfrac{\Delta_1}{\delta_1})\\ c_{n-1}(\delta_{n-1})+c_n(2\delta_{n-1})=3(v_2-\dfrac{\Delta_{n-1}}{\delta_{n-1}})\\ \end{array} \]
- 矩阵中表现为(还是严格对角占优)
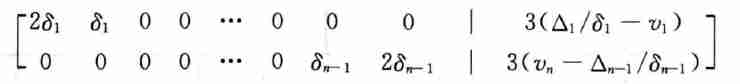
抛物线端点的三次样条
- \(d_1=d_n=0\)
- 让样条的起始和结束至多为 \(2\) 阶
- 等价于:\(c_1=c_2,c_{n-1}=c_n\)
- 矩阵中表现为(不是严格对角占优)

- 通过变换我们发现还是具有唯一解
- 假设数据点的个数 \(n\ge3\)
- 通过用 \(c_2\) 替换 \(c_1\),\(c_{n-1}\) 替换 \(c_n\),我们发现矩阵方程简化为关于 \(c_2,\cdots,c_{n-2}\) 的 \((n-2)\times(n-2)\) 的严格对角占优矩阵
- 唯一解
非纽结三次样条
- 起始(终止)曲线的两端三阶导数相同 \(\Rightarrow\) \(d_1=d_2,d_{n-2}=d_{n-1}\) \(\Rightarrow\) \(S_1=S_2,S_{n-1}=S_{n-2}\)
- 式子
\[ \begin{array}{c} \dfrac{c_2-c_1}{\delta_1}=\dfrac{c_3-c_2}{\delta_2}\\ \dfrac{c_{n-2}-c_{n-1}}{\delta_{n-1}}=\dfrac{c_{n-1}-c_{n}}{\delta_{n}}\\ \end{array} \]
\[ \begin{array}{c} c_1(\delta_2)-c_2(\delta_1+\delta_2)+c_3(\delta_1)=0\\ c_{n-2}(\delta_{n-1})-c_{n-1}(\delta_{n-2}+\delta_{n-1})+c_{n}(\delta_{n-2})=0\\ \end{array} \]
- 矩阵中表现为
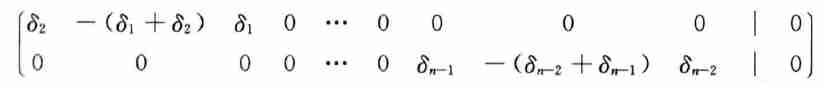
5. 贝塞尔曲线
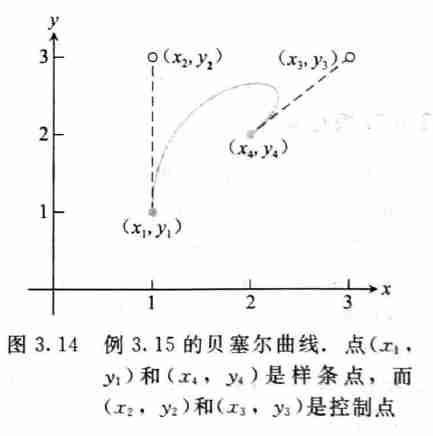
- 平面贝塞尔曲线由 \(4\) 个点组成
- 起点 \((x_1,y_1)\),起点 \((x_4,y_4)\)
- 控制点 \((x_2,y_3),(x_3,y_3)\)
- 曲线以切线方向 \((x_2-x_1,y_2-y_1)\) 离开 \((x_1,y_1)\),以切线方向 \((x_4-x_3,y_4-y_3)\) 回到 \((x_4,y_4)\)
贝塞尔曲线

- 性质
\[ \begin{array}{c} x(0)=x_1\\ x'(0)=3(x_2-x_1)\\ x(1)=x_4\\ x'(1)=3(x_4-x_3)\\ \end{array} \]