计算方法B.裴玉茹.04.插值
- 数值分析课本第 3 章(插值) + PPT(多项式插值)
插值
1. 数据和插值函数
- 如果对于每个 \(1\le i\le n\),\(P(x_i)=y_i\),则称函数 \(y=P(x)\) 插值数据点 \((x_1,y_1),\cdots,(x_n,y_n)\)
- 要求 \(P\)
是函数,对数据点有限制
- 即要求不能存在两个数据点的 \(x\) 值相同而 \(y\) 值不同
- 要求 \(P\)
是函数,对数据点有限制
- 为什么使用多项式进行插值

1.1 拉格朗日插值
- \(3\) 个数据点 \((x_1,y_1),(x_1,y_2,(x_3,y_3)\) 的拉格朗日插值多项式如下
\[ P_{2}(x) =y_1\dfrac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} +y_2\dfrac{(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)} +y_3\dfrac{(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} \]
- 容易验证经过 \(3\) 个数据点
- 一般的,对于 \(n\) 个数据点 \((x_1,y_1),\cdots,(x_n,y_n)\),插值多项式如下
\[ P_{n-1}(x)=\sum_{i=1}^{n}y_iL_i(x) \]
\[ L_k(x)=\prod_{i=1,i\ne{k}}^{n}\dfrac{(x-x_i)}{(x_k-x_i)} \]
多项式插值的主定理
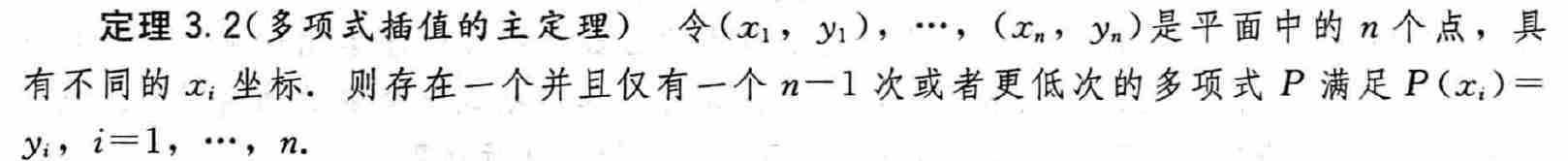
- 存在性:拉格朗日插值多项式给出
- 唯一性:假设存在两个不同的痛的多项式 \(P(x),Q(x)\),证明 \(P(x)-Q(x)\equiv0\)
- \(n\) 阶多项式最多有 \(n\) 个过零点

- 多项式可能比 \(n-1\) 阶更低
- 例如三个数据点,如果 3 点共线,那么插值函数退化为一条直线
- 拉格朗日很少用于计算,这是由于其他方法可以得到控制能力更强,同时计算代价更低的多项式
- 本质上所有的插值多项式都和拉格朗日插值多项式相同,只是以不同的形式给出
1.2 牛顿差商
- 定义
- \(f[{x_1}\cdots{x_n}]\)
表示(唯一)多项式的 \(x^{n-1}\)
项系数,该多项式插值 \((x,f(x_1)),\cdots,(x_n,f(x_n))\)
- 只表示最高次项的系数
- \(f[{x_1}\cdots{x_n}]\)
表示(唯一)多项式的 \(x^{n-1}\)
项系数,该多项式插值 \((x,f(x_1)),\cdots,(x_n,f(x_n))\)
牛顿差商公式
\[ \begin{aligned} P(x)&=f[x_1]\\ &+f[x_1x_2](x-x_1)\\ &+f[x_1x_2x_3](x-x_1)(x-x_2)\\ &+\cdots\\ &+f[x_1\cdots{x_n}](x-x_1)\cdots(x-x_{n-1}) \end{aligned} \]
- 具体系数可以通过递归定义计算
\[ \begin{aligned} f[x_k]&=f(x_k)\\ f[x_kx_{k+1}]&=\dfrac{f[x_{k+1}]-f[x_k]}{x_{k+1}-x_k}\\ f[x_kx_{k+1}x_{k+2}]&=\dfrac{f[x_{k+1}x_{k+2}]-f[x_kx_{k+1}]}{x_{k+2}-x_k}\\ &\cdots\\ \end{aligned} \]
插值证明
系数计算
- 从低阶差商开始计算
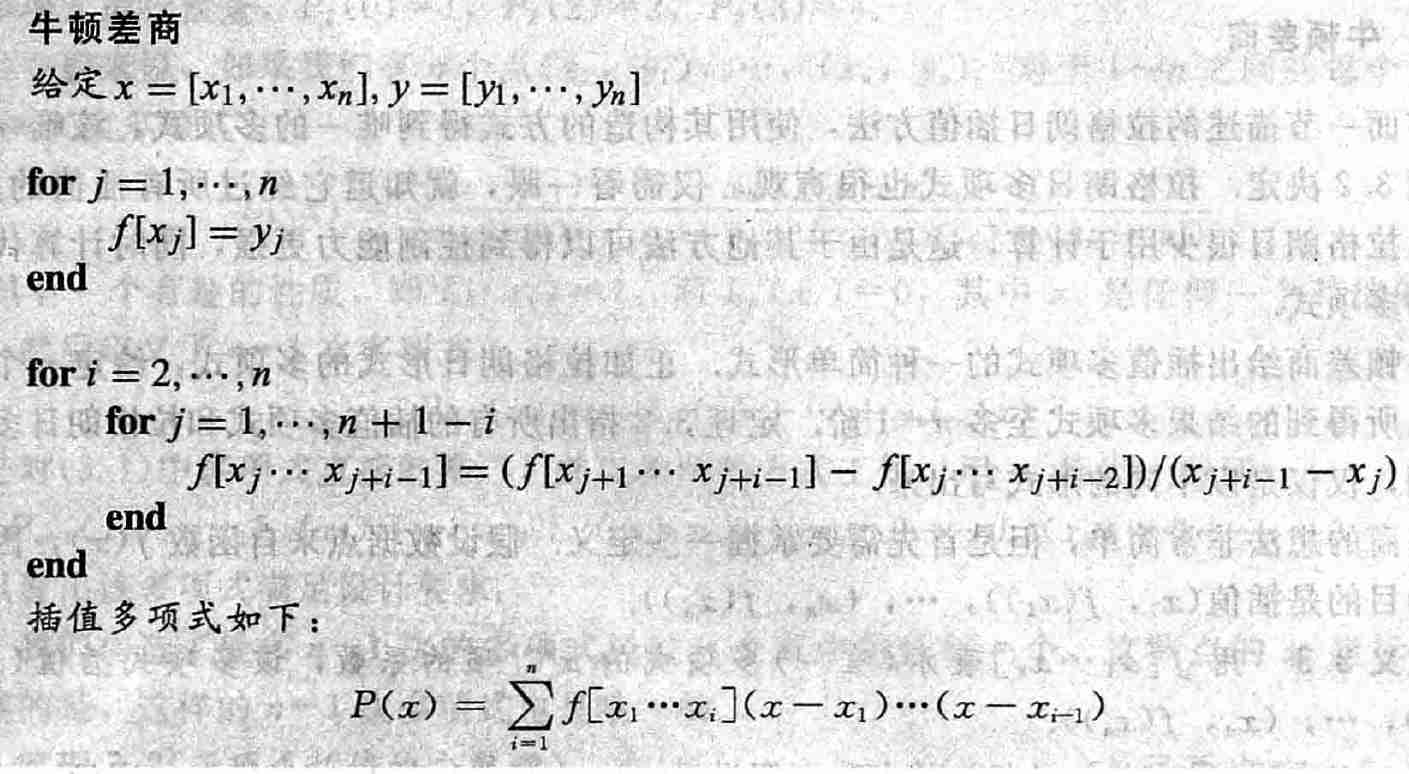
- 用表的形式计算
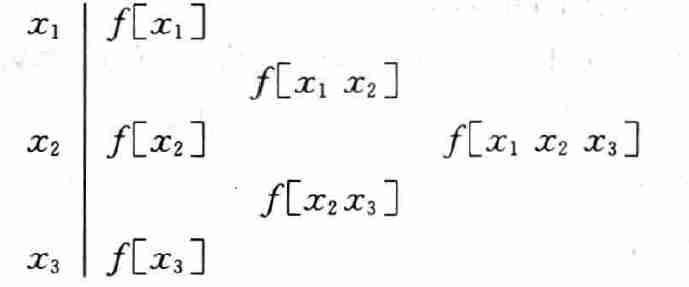
特点
- 如果有新加入的点
- 拉格朗日插值多项式需要全部重新计算
- 牛顿插值多项式可以利用之前的计算值实时更新
1.3 经过 \(n\) 个点的 \(d\) 阶多项式有多少个
- 经过 \(n\) 个点的插值多项式为 \(r\) 阶,其中 \(1\le{r}\le{n-1}\)
- 如果 \(d<r\):不存在这样的多项式
- 如果 \(d=r\):存在 \(1\) 个这样的多项式
- 如果 \(d>r\):存在无穷多个这样的多项式
- \(P_r(x)+c\prod_{i=1}^{n}(x-x_k)\)
- 可以通过控制后面多项式 \(x_i\) 的个数,从而控制阶数
1.4 插值代码
1.5 通过近似多项式表示函数
- 插值多项式是对实际函数 \(f(x)\)
的一个压缩
- 有损压缩
- 在给定的某个区间中进行取点,然后使用多项式插值
- 区间内可以得到较小的误差
2. 插值误差
2.1 插值误差公式

- 通常误差公式很难计算,但是可以给出一个误差界
- 在区间的中部,插值误差可能会变得更小
2.2 牛顿形式和误差公式的证明
- 令 \(P(x)\) 表示(唯一插值)\((x_1,f(x_1)),\cdots,(x_n,f(x_n))\)的多项式
- 其中 \({\color{red}a_{n-1}=f[x_1\cdots
x_n]}\) 表示 \({\color{red}n-1}\) 阶的系数
- 仅仅是 \(n-1\) 阶,其他不一定满足
- 其中 \({\color{red}a_{n-1}=f[x_1\cdots
x_n]}\) 表示 \({\color{red}n-1}\) 阶的系数
\[ P(x)=a_0+a_1x+a_2x^2+\cdots a_{n-1}x^{n-1} \]
- 事实1
- 由于插值多项式的唯一性,对于 \(x_i\) 的任意排列 \(\sigma\),都有 \(f[x_1\cdots x_n]=f[\sigma(x_1)\cdots \sigma(x_n)]\)
- 事实2
- \(P(x)\) 可以表示为另外一种形式
- \(c_{n-1}=a_{n-1}\),然后从高阶到低阶一步一步确定剩下的系数 \(c_{n-1},\cdots,c_0\)
\[ P(x)=c_0+c_1(x-x_1)+c_2(x-x_1)(x-x_2)+\cdots+\Big[c_{n-1}(x-x_1)(x-x_2)\cdots(x-x_{n-1})\Big] \]
牛顿插值多项式的证明
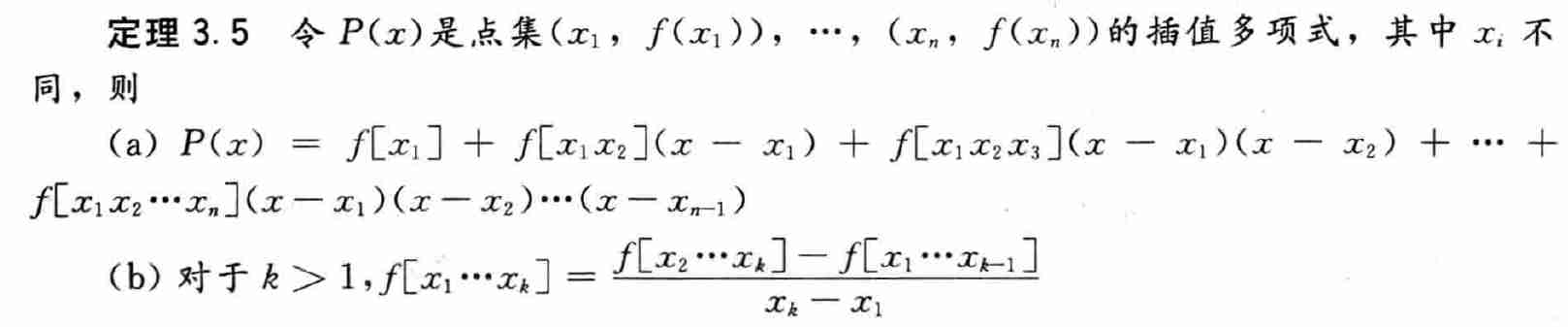
- 证明思路:先证明事实2中的系数为 \(c_{i-1}=f[x_1\cdots x_{i}]\),然后证明
\(c_i\) 的递推关系,\(f[x_1\cdots x_{i}]\) 的定义如上
- 证明 \((a)\)
- 先证明 \((a)\) 中最高次项系数 \(c_{n-1}=f[x_1\cdots x_{n-1}]=a_{n-1}\)
- 这个本质上就已经证明了每一个系数就是 \(c_{k-1}=f[x_1\cdot x_{n}],k=1,\cdots,n\)
- 对于 \(P(x_1),\cdots,P(x_k)\),只有前 \(k\) 项非零,说明前 \(k\) 项是 \(x_1,\cdots,x_{k}\) 的插值多项式
- 插值多项式的唯一性
- 证明 \((b)\)
- 证明系数递推的具体形式
- 证明 \((a)\)

插值误差证明

2.3 龙格现象
- \(f(x)=\dfrac{1}{1+12x^2}\) 在 \([-1,1]\) 均匀分布点集的插值
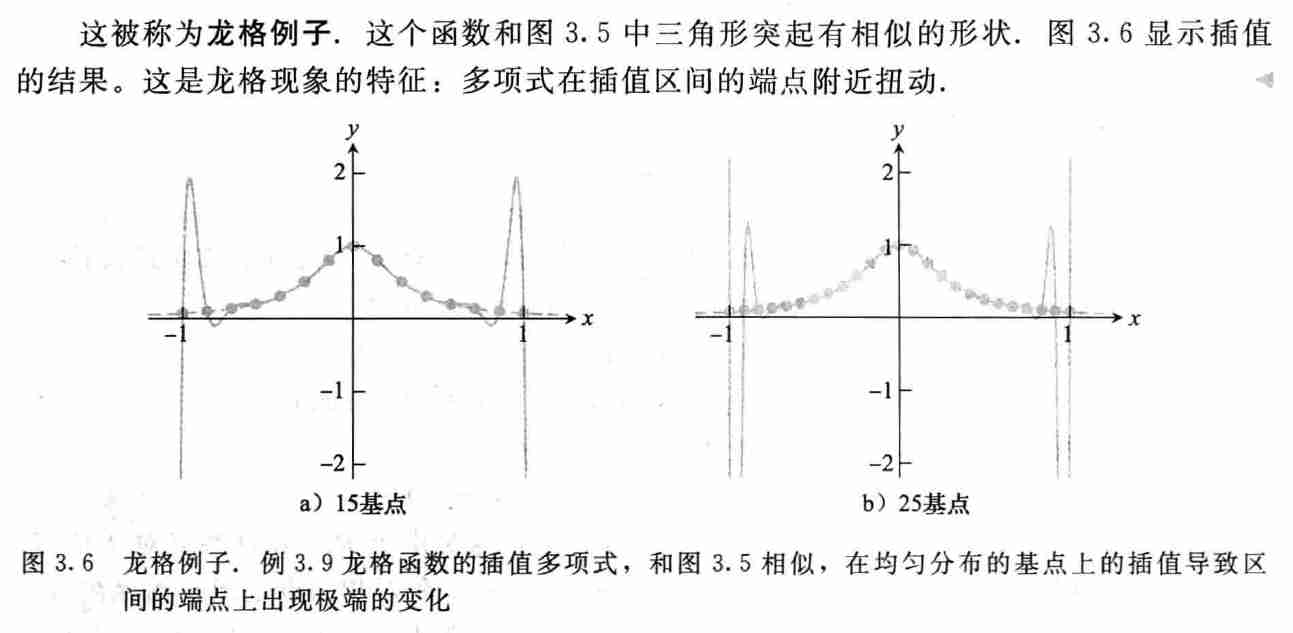
- 龙格现象:多项式在插值区间的端点附近扭动
- 龙格现象的例子在数据点区间端点外有非常大的误差
- 解决方法:将一些插值点移动到区间的外面,在那里函数生成的点可以使拟合的效果更好
3. 切比雪夫插值
- 使用平均分布的点作为插值多项式的基点 \(x_i\) 很普遍,在很多情况下,用于插值的数据点仅以这种形式存在,例如当数据由相同时间间隔分布的仪器读取的数据所组成时,在其他情况下,例如 sine 键问题中,我们可以在认为合适的地方自由选取基点,事实证明,基点间距选取的方式对于插值误差有很大的影响。
- 切比雪夫插值是一种特定最优的点间距选取方式
3.1 切比雪夫理论
- 切比雪夫插值的动机:在插值区间上,提高对如下插值误差的最大值的控制
\[ \dfrac{(x-x_1)\cdots(x-x_n)}{n!}f^{(n)}(c) \]
- 固定区间为 \([-1,1]\)
插值误差的最小最大问题
- 在区间 \([-1,1]\) 内找到特定的 \(x_1,\cdots,x_n\) 使得分子 \((x-x_1)\cdots(x-x_n)\) 的最大值足够小
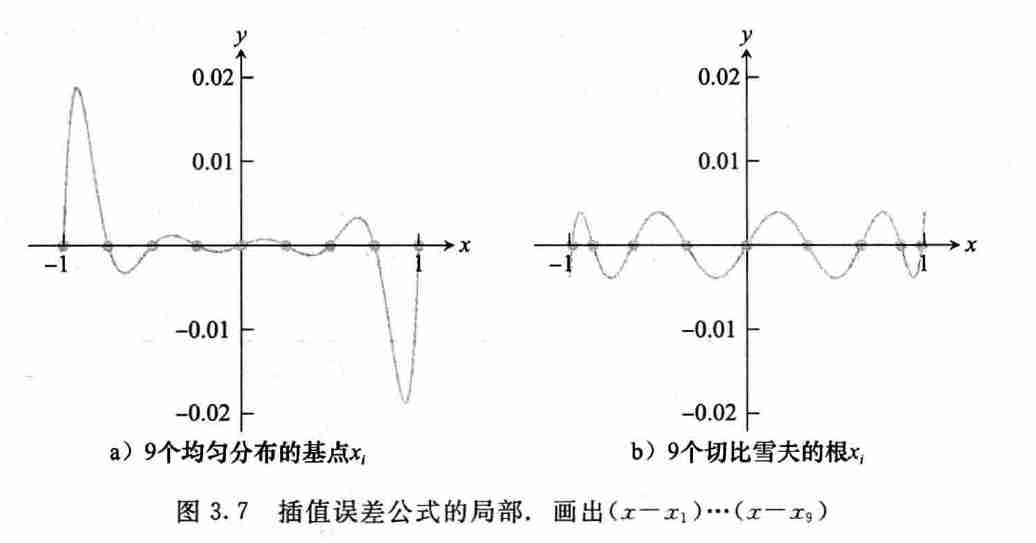
切比雪夫定理

切比雪夫插值多项式
- 选择切比雪夫的根作为插值的基点,在区间 \([-1, 1]\) 中尽可能均匀地分散了插值误差
\[ x_i=\cos\dfrac{i\pi}{2n},\qquad i=1,\cdots,n \]
- 我们将使用切比雪夫根作为基点的插值多项式叫做切比雪夫插值多项式
一个例子
- \(f(x)=\dfrac{1}{12x^2+1}\)
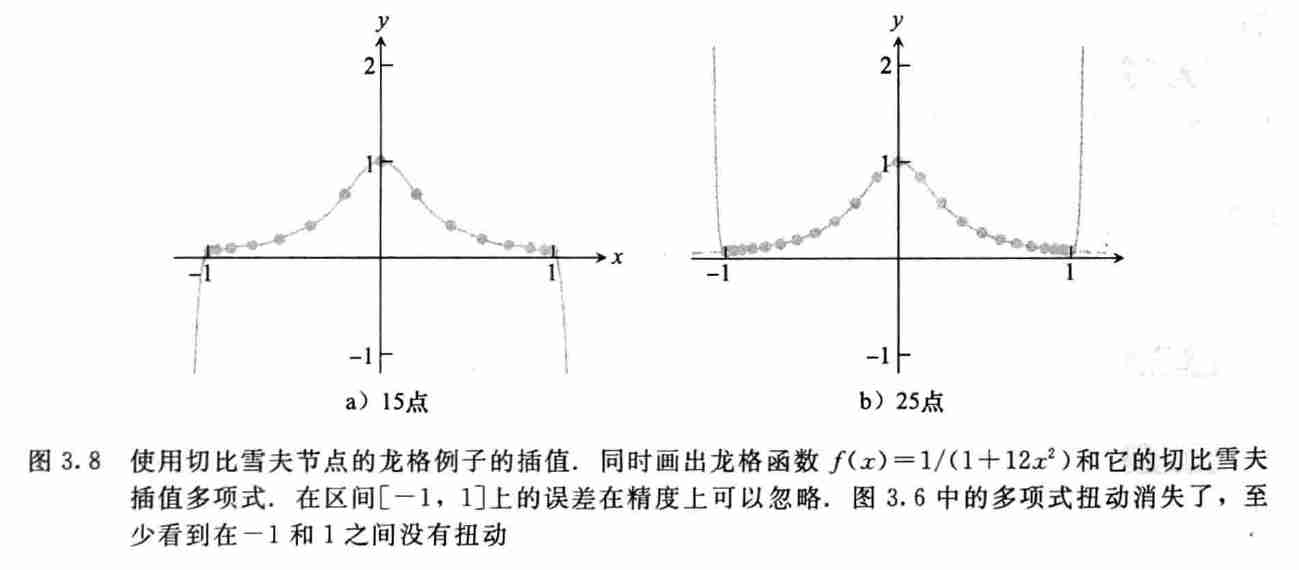
- 和上面的均匀选取插值点对比,龙格现象消失了
3.2 切比雪夫多项式
- \(n\) 阶切比雪夫多项式
\[ T_n(x)=\cos(n\arccos{x}) \]
- 对于每个 \(n\) 都是关于 \(x\) 的多项式
\[ \begin{array}{ll} n=0:&T_1(x)=1\\ n=1:&T_2(x)=x\\ n=2:&T_2(x)=2x^2-1\\ \end{array} \]
- 递推公式,记 \(y=\arccos{x}\Rightarrow x=\cos{y}\)
\[ T_{n+1}(x)=\cos(n+1)y=\cos{ny}\cos{y}-\sin{ny}\sin{y} \]
\[ T_{n-1}(x)=\cos(n-1)y=\cos{ny}\cos{y}+\sin{ny}\sin{y} \]
\[ T_{n+1}(x)+T_{n-1}(x)=2xT_{n}(x) \]
- 得到递推公式
\[ T_{n+1}(x)=2xT_{n}(x)-T_{n-1}(x) \]
一些事实
- 切比雪夫多项式 \(T_n\) 确实都是关于 \(x\) 的多项式
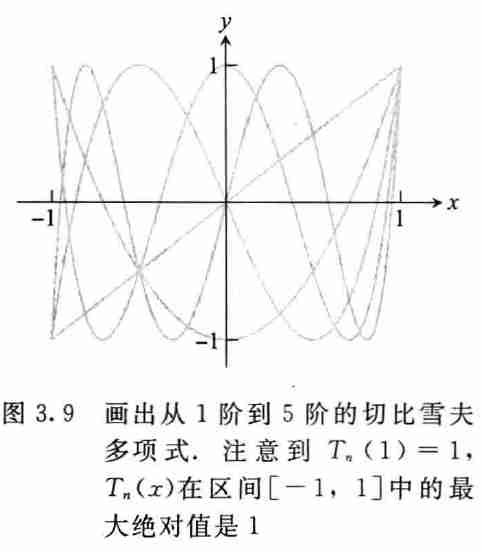
- \(\deg(T_n)=n\),主导系数是 \(2^{n-1}\)
- deg:多项式最高次项的次数
- 主导系数:多项式最高次项的系数
- \(T_n(1)=1,T_n(-1)=(-1)^{n}\)
- \(\vert{T_n(x)}\vert\le1,x\in[-1,1]\)
- \(T_n(x)=\cos(ny)\) 显然成立
- \(T_n(x)\) 的所有过零点都在 \([-1,1]\) 之间
\[ \begin{aligned} &\cos(n\arccos{x})=0\\ \Rightarrow&n\arccos{x}=\mathrm{odd}\cdot\dfrac{\pi}{2}\\ \Rightarrow&x=\cos{\left(\mathrm{odd}\cdot\dfrac{\pi}{2n}\right)}\\ \end{aligned} \]
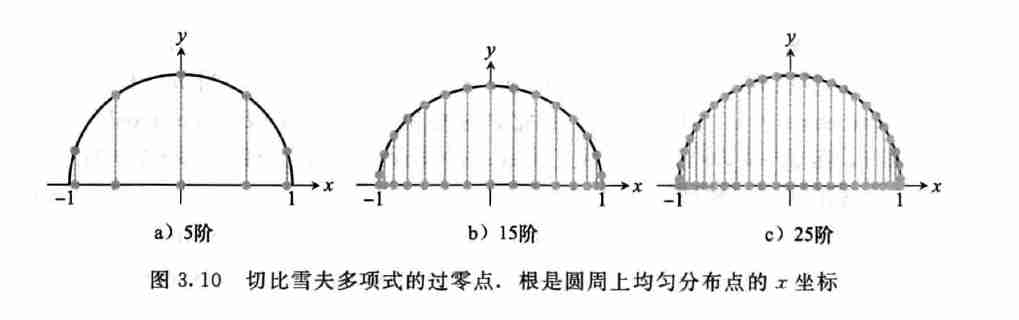
- \(T_n(x)\) 在 \([-1,1]\) 之间一共往返 \(n+1\) 次,发生在 \(\cos{\dfrac{i\pi}{n}},i=0,\cdots,n\)
- 对于多项式 \(T_{n}(x)\)
- \(\dfrac{T_n(x)}{2^{n-1}}\) 为首一多项式(主导系数为 \(1\))
- \(x_i\) 为切比雪夫不等式 \(T_n(x)\) 的过零点,那么有
\[ \dfrac{T_n(x)}{2^{n-1}}=\prod_{i=1}^{n}(x-x_i) \]
切比雪夫定理的证明

- \(\vert{t}\vert<\dfrac{1}{2^{n-1}}\Rightarrow{t-(-\dfrac{1}{2^{n-1}})>0,t-(\dfrac{1}{2^{n-1}})<0}\)
3.3 区间的变化
- \([-1,1]\to[a,b]\)
- 相对位置不变:拉伸 + 平移
\[ \begin{array}{c} x_i=\cos{\left(\mathrm{odd}\cdot\dfrac{\pi}{2n}\right)}\\ \Rightarrow\\ x_i=\dfrac{b-a}{2}\cos{\left(\mathrm{odd}\cdot\dfrac{\pi}{2n}\right)}+\dfrac{a+b}{2} \end{array} \]
- 上界发生变化:相当于对因子 \(x-x_i\) 做了拉伸
\[ \dfrac{1}{2^{n-1}}\Rightarrow\left(\dfrac{b-a}{2}\right)^{n}\dfrac{1}{2^{n-1}} \]
- 切比雪夫插值节点

- 切比雪夫多项式是将一般函数转化为少量浮点计算的一种好的方式
- 可以简化计算
- 容易得到误差上界,这个误差上界通常比均匀分布的插值的误差小,并且可以根据需要把它变得足够小
CORDIC
- CORDIC (坐标旋转数字计算机)算法
- 计算器中用于近似 \(\sin,\cos\) 的算法
- 基于复数算术的迭代算法