计算方法B.裴玉茹.03.方程组(4)

Posted on Edited on In Views:
PPT 补充、不动点迭代、牛顿法、Broyden 方法、最速下降方法（转化为最优化问题）、同伦和延拓方法（转化为常微分方程的初值问题）
  • 数值分析课本第 2 章（方程组） + PPT（非线性方程组迭代求解）

非线性方程组迭代求解方法

  • PPT 补充

1. 不动点迭代

  • 一样的定义，多变量非线性方程组

\[ F(x)=0 \]

  • 不动点 \(p\)

\[ p=G(p) \]

  • 函数 \(g:\mathbb{R}^{n}\to{\mathbb{R}}\) 定义在集合 \(D\in{\mathbb{R}^{n}}\) 上, 当 \(p=G(p),p\in{D}\) 为不动点.

函数连续

  • 函数 \(f:\mathbb{R}^{n}\to{\mathbb{R}}\) 定义在 \(D\in{\mathbb{R}^{n}}\) 上，如果函数 \(f\) 的所有偏导数存在并且存在常数 \(\delta>0,K>0\)，当 \(\Vert{x-x_0}\Vert<\delta\)，使得 \(\dfrac{\partial{f(x)}}{\partial{x_j}}\le{K},j=1,2,\cdots,n\) ，则函数在 \(x_0\) 连续

不动点定理

  • 连续、自身映射、小于 \(\dfrac{1}{n}\)

  • 充分不必要条件

不动点迭代方法

Gauss-Seidel 方法

  • 和之前相同，直接使用这一轮计算出来得到的值

2. 牛顿法

  • 另外一种思路

\[ G(x)=x-A(x)^{-1}F(x) \]

  • \(B=A^{-1}\)

\[ g_{i}(x)=x_i-\sum_{j=1}^{n}b_{ij}f_j(x) \]

  • 导数为 0

\[ \dfrac{\partial{g_{i}}}{\partial{x_k}}(x)=0 \]

  • 那么有如下式子
    • \(f_{j}(x)=0\)

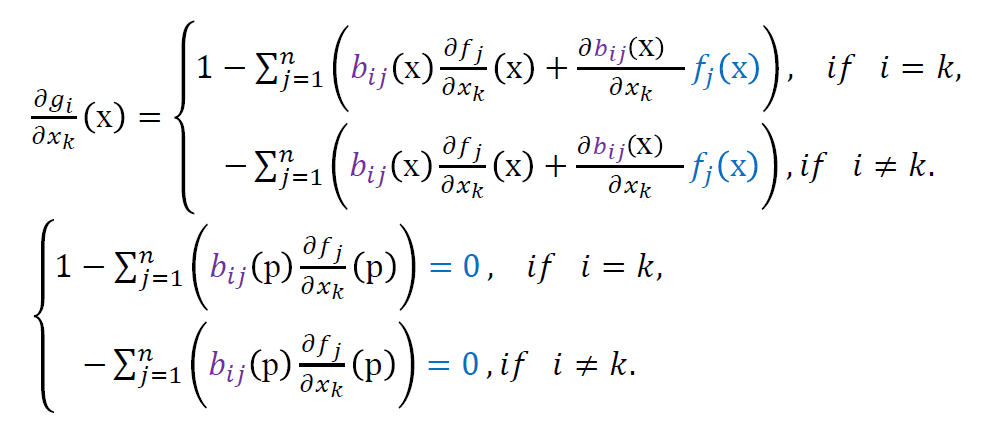
  • 可以得到 \(A=J(x)\)
    • \(J(x)\)：雅可比矩阵（Jacobian）

牛顿方法的二阶收敛

  • 一旦获取在真实解附近的近似值，牛顿方法可以收敛极快

加速

  • 避免计算 \(J(x)^{-1}\)：高斯消去替代

3. 拟牛顿方法

Broyden 算法

  • 利用每步中更新的近似矩阵替换牛顿方法中的雅各比矩阵
  • 超线性收敛

\[ \lim_{i\to\infty}\dfrac{\Vert{x^{(i+1)}-p}\Vert}{\Vert{x^{(i)}-p}\Vert}=0 \]

  • 使用差分方程近似偏导数
    • \(n^2\) 次函数计算

\[ \dfrac{\partial{f_j}}{\partial{x_k}}(x^{(i)})\approx\dfrac{f_j(x^{(i)}+e_{k}h)-f_j(x^{(i)})}{h} \]

  • 其中

\[ e_{k}=(0,0,\cdots,1,\cdots,0) \]

算法

  • 一个 \(n\) 维向量的 \(v\) 正交补向量一共有 \(n-1\) 个
    • 由 \(v\) 可以生成 \(\mathbb{R}^n\) 的一组正交基，剩下的 \(n-1\) 个向量都和 \(v\) 垂直
  • 那么此时我们有 \(n^2\) 个方程，理论上可以解出 \(A_1\)
    • \(A_1(x^{(1)}-x^{(0)})=F(x^{(1)}-x^{(0)})\) 中 \(n\) 个
    • \(\big(A_1-J(x^{(0)})\big)z=0\) 中 \(n(n-1)\) 个
  • \(n\) 次函数的函数计算

与牛顿法的对比

Broyden Newton
函数值计算次数 \(n\) \(n^2+n\)
（雅可比矩阵 \(n\) 次计算）
解线性方程组 \(n^3\) \(n^3\)
超线性收敛 二次收敛

Sherman-Morrison 公式

  • 之前提到的 Broyden II 方法，直接更新 \(A^{-1}\)，而不是 \(A\)

Sherman-Morrison 公式

  • 如果 \(A\) 为非奇异矩阵，\(x\) 与 \(y\) 为向量, 则 \(A+xy^{t}\) 为非奇异矩阵，如果 \(y^{t}A^{-1}x\ne-1\) ，则

\[ (A+xy^{t})^{-1}=A^{-1}-\dfrac{A^{-1}xy^{t}A^{-1}}{1+y^{t}A^{-1}x} \]

  • 如此可以在迭代的过程中避免求逆

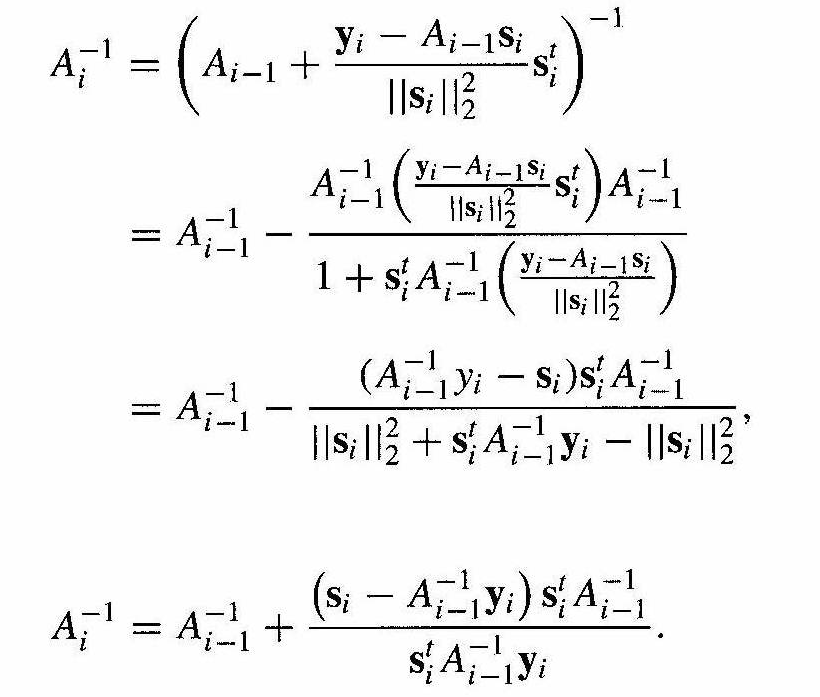
  • Broyden 方法一般收敛更慢，但是计算相对简单

4. 最速下降方法

  • 将求非线性方程组的解转化为函数最小化问题

转化

  • 考虑非线性方程组

\[ \begin{array}{c} f_{1}(x_{1},x_{2},\cdots,x_{n})=0\\ f_{2}(x_{1},x_{2},\cdots,x_{n})=0\\ \cdots\\ f_{n}(x_{1},x_{2},\cdots,x_{n})=0\\ \end{array} \]

  • 该非线性方程组的解 \(x=(x_{1},x_{2},\cdots,x_{n})^{t}\) ，使得如下函数 \(g\) 具有最小值

\[ g(x_{1},x_{2},\cdots,x_{n})=\sum_{i=1}^{n}\big[f_{i}(x_{1},x_{2},\cdots,x_{n})\big]^{2} \]

算法流程

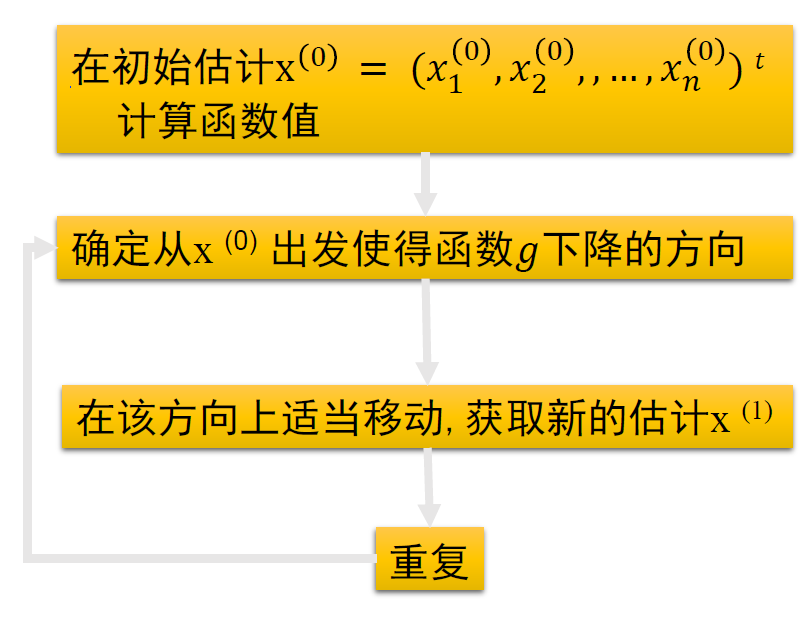
定义

梯度

  • 函数 \(g:\mathbb{R}^{n}\to{\mathbb{R}}\) , 在 \(x=(x_{1},x_{2},\cdots,x_{n})^{t}\) 的梯度定义如下

\[ \nabla{g(x)}=\left({\dfrac{\partial{g}}{\partial{x_1}}(x)},{\dfrac{\partial{g}}{\partial{x_2}}(x)},\cdots,{\dfrac{\partial{g}}{\partial{x_n}}(x)}\right)^{t} \]

  • 当在 \(x\) 点的梯度为 \(0\) 向量时，多变量函数在 \(x\) 点具有极小值

单位向量

  • 单位向量 \(v\)

\[ \Vert{v}\Vert_2^2=\sum_{i=1}^{n}v_i^{2}=1 \]

方向导数

  • \(D_{v}g(x)\) 度量函数 \(g\) 值在方向 \(v\) 上的变化

\[ D_{v}g(x)=\lim_{h\to0}\dfrac{1}{h}\left[g(x+hv)-g(x)\right]=v^{t}\cdot\nabla{g(x)} \]

  • 函数 \(g\) 的最速下降方向为负梯度方向 \(-\nabla{g(x)}\)

算法

  • \(x^{(1)}=x^{(0)}-\alpha\nabla{g(x)}\)
  • 确定 \(\alpha\) 使得如下函数 \(h\) 最小化

\[ h(\alpha)=g\left({x^{(0)}-\alpha\nabla{g(x^{(0)})}}\right) \]

  • 如何选择 \(\alpha\)
    • 多项式近似原始复杂的函数函数，利用多项式极值代替函数极值
  • \(\alpha_1<\alpha_2<\alpha_3\)，计算函数值 \(h(\alpha)\)，估计多项式极值
  • 构造二阶插值多项式 \(P(x)\)
  • 确定 \(P(\hat{\alpha}),\hat{\alpha}\in[\alpha_1,\alpha_3]\)，使得函数 \(h(\alpha)\) 最小化
  • \(x^{(1)}=x^{(0)}-\hat{\alpha}\nabla{g(x)}\)

如何选择这三个点

  • \(\alpha_1=0:h(\alpha_1)=h(0)=g(x^{(0)})\)
  • 选定 \(\alpha_3\) 满足 \(h(\alpha_3)<h(\alpha_1)\)
    • 初始选择 \(\alpha_3=1\)
    • 当 \(h(\alpha_3)>h(\alpha_1)\)，令 \(\alpha_3=2^{-k}\)，直到 \(h(\alpha_3)<h(\alpha_1)\)
    • 因为是负梯度方向，一定能够取到满足上面的 \(\alpha_3\)
  • \(\alpha_2\) 可以选择 \(\dfrac{\alpha_3}{2}\)
  • 根据我们的选择，多项式 \(P\) 的极值点可以出现在临界点或者区间的右端点

5. 同伦和延拓方法

  • 考虑一组问题 \(G:[0,1]\)

\[ G:[0,1]\times\mathbb{R}^{n}\to\mathbb{R}^{n} \]

\[ G(\lambda,x)=\lambda{F(x)}+(1-\lambda)[F(x)-F(x{(0)})]=F(x)+(1-\lambda)F(x{(0)}) \]

  • 同伦与延拓

image-20211015114551294

问题描述

  • 从 \(G(0, x)=0\) 的已知解 \(x(0)\)，求解函数 \(G (1,x)\) 的根 \(x(1)=x^{\ast}\)
    • \(G(\lambda,x),\lambda\in[0,1]\)
  • 假设 \(x(\lambda)\) 是 \(G(\lambda,x)=0\) 的唯一解
  • 如果函数 \(\lambda\to{x(\lambda)},G(\lambda,x)\) 可微, 对 \(G(\lambda,x)=0\) 关于 \(\lambda\) 求导
  • \(G(\lambda,x)\) 对 \(\lambda\) 求导

\[ \dfrac{\partial{G(\lambda,x(\lambda))}}{\partial{\lambda}} +\dfrac{\partial{G(\lambda,x(\lambda))}}{\partial{x}}x'(\lambda) =0 \]

  • 得到

\[ x'(\lambda)=-\left[{\dfrac{\partial{G(\lambda,x(\lambda))}}{\partial{x}}}\right]^{-1}\dfrac{\partial{G(\lambda,x(\lambda))}}{\partial{\lambda}} \]

  • 转化为一个常微分方程的初值问题
    • 初值 \(x(0)\) 已知
    • 知道 \(x'(\lambda),\lambda\in[0,1]\)

细节

\[ G(\lambda,x)=F(x)+(\lambda-1)F(x{(0)}) \]

  • 两个偏导数结果如下

\[ \dfrac{\partial{G(\lambda,x(\lambda))}}{\partial{x}} =\dfrac{\partial{F(x(\lambda))}}{\partial{x}} =J(x(\lambda)) \]

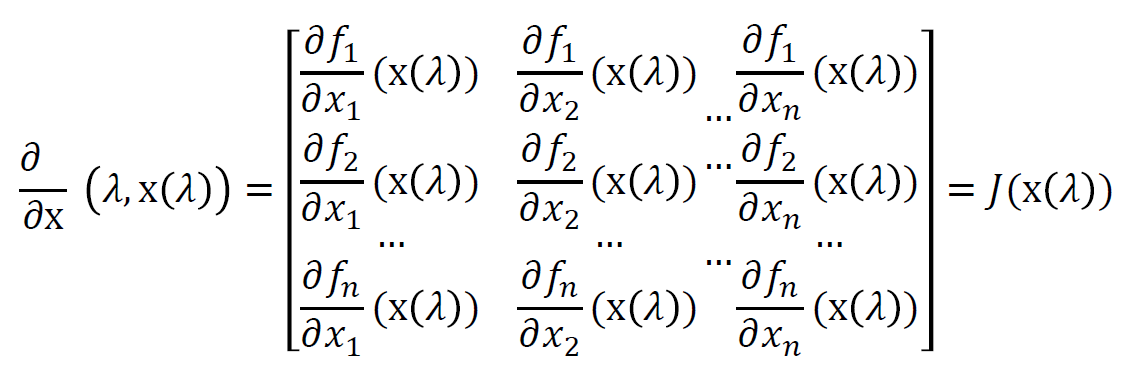\[ \dfrac{\partial{G(\lambda,x(\lambda))}}{\partial{\lambda}} =F(x(0)) \]

  • 常微分方程的初值问题

\[ x'(\lambda)={J\big(x(\lambda)\big)}^{-1}F(x(0)),\lambda\in[0,1] \]

完整描述

解法

  • Runge Kutta 方法等