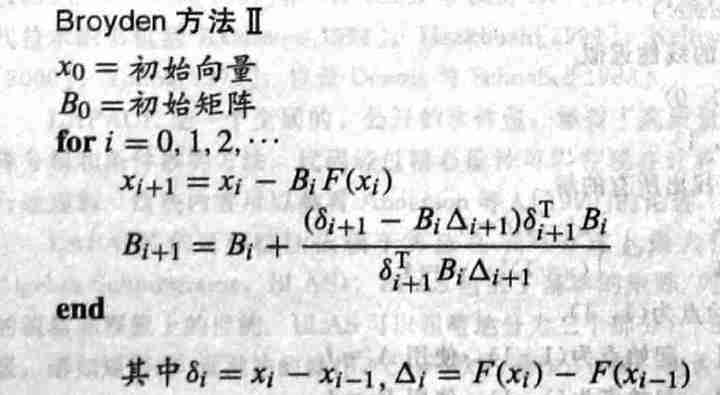计算方法B.裴玉茹.03.方程组(3)

Posted on Edited on In Views:
用于对称正定矩阵的方法（楚列夫斯基分解）、非线性方程组求解（牛顿法、Broyden 方法）
  • 数值分析课本第 2 章（方程组） + PPT（非线性方程组迭代求解）

方程组

6. 用于对称正定矩阵的方法

  • 楚列夫斯基（Cholesky） 分解

6.1 对称正定矩阵

正定矩阵定义与性质

  • 对称矩阵：\(A^{T}=A\)
  • 正定矩阵：对任意的向量 \(x\ne0\)，都有 \(x^{T}Ax>0\)
  • 对称正定矩阵是非奇异矩阵
    • 不存在非零向量 \(x\) 使得 \(Ax=0\)
  • \(A\) 是正定矩阵 \(\Leftrightarrow\) \(A\) 的所有特征值为正数

  • \(n\times n\) 的对称正定矩阵 \(A\)，\(n\times m\) 的满秩矩阵 \(X\)（\(n\ge m\)），则 \(X^{T}AX\) 是 \(m\times m\) 的对称正定矩阵
    • 对称：\((X^{T}AX)^{T}=X^{T}AX\)
    • 正定：非零 \(m\) 维向量 \(v\)，\(v^{T}(X^{T}AX)v=(Xv)^{T}A(Xv)\)
      • \(A\) 是正定矩阵，如果 \(Xv\ne0\) ，则 \(v^{T}(X^{T}AX)v>0\)
      • \(X\) 满秩 \(\Rightarrow\) 列向量线性无关 \(\Rightarrow\) \(Xv=0\Leftrightarrow v=0\)
        • \(Xv\) 是对 \(X\) 列向量的线性组合

主子矩阵

  • 任何对称正定矩阵的主子矩阵也是对称正定矩阵
  • 假设主子矩阵 \(M\) 选中的是第 \(i_1,i_2,\cdots,i_k\) 列，那么他选中的就是第 \(i_1,i_2,\cdots,i_k\) 行
  • 任意向量 \(v=(v_1,\cdots,v_k)^{T}\)

\[ \begin{aligned} v^{T}Mv&=\sum_{y=1}^{k}\sum_{x=1}^{k}v_xm_{x,y}v_y\\ &=\sum_{y=1}^{k}\sum_{x=1}^{k}v_xa_{i_{x},i_{y}}v_y \end{aligned} \]

  • 构造向量 \(u\)，满足如下结果

\[ u_j= \left\{ \begin{array}{ll} v_k&j=i_k\\ 0&else\\ \end{array} \right. \]

  • 那么有

\[ \begin{aligned} u^{T}Au&=\sum_{y=1}^{n}\sum_{x=1}^{n}u_xa_{x,y}u_y\\ &=\sum_{y=1}^{k}\sum_{x=1}^{k}u_{i_x}a_{i_{x},i_{y}}u_{i_y}\\ &=\sum_{y=1}^{k}\sum_{x=1}^{k}v_xa_{i_{x},i_{y}}v_y \end{aligned} \]

  • 所以

\[ v^{T}Mv=u^{T}Au>0 \]

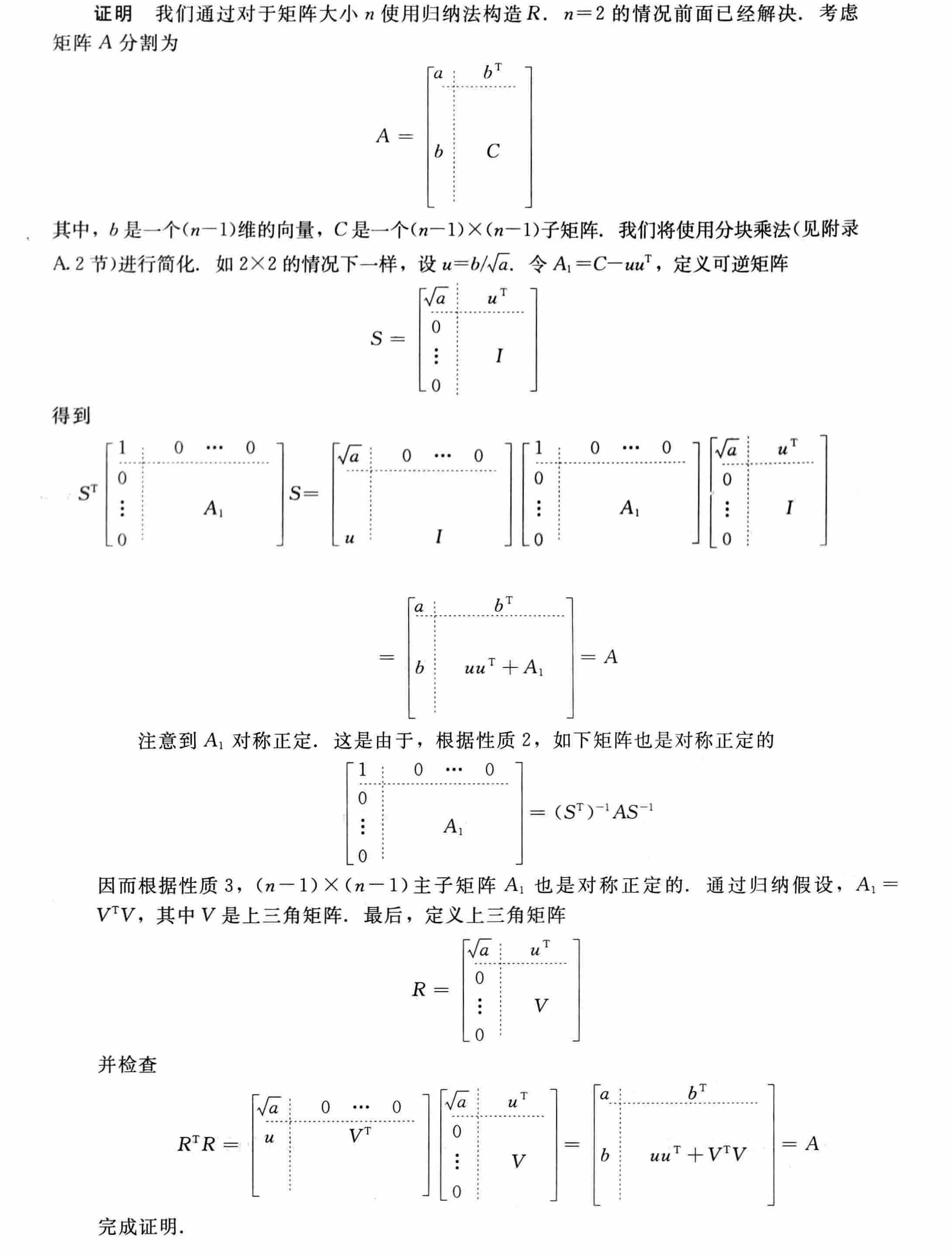
6.2 楚列斯基分解

  • 如果 \(A\) 是 \(n\times n\) 对称正定矩阵，则存在 \(n\times n\) 上三角阵 \(R\)，满足 \(A=R^{T}R\)

归纳法证明

  • \(n=2\) 时

  • \(n\ge2\)

分解算法

  • 结果生成的矩阵为上三角矩阵 \(R\)

解方程

  • \(Ax=b\)
  • \(R^{T}Rx=b\)
  • \(R^{T}y=b,Rx=y\)

6.3 共轭梯度方法

  • 向量内积是对称的、线性的

\[ (w,v)=(v,w) \]

\[ (\alpha w+\beta v,u)=\alpha(w,u)+\beta(v,u) \]

A 内积与 A 共轭

  • 对称正定矩阵 A 的 A 内积和 A 共轭

  • A 内积继承了矩阵 A 的线性、对称、正定性质
  • A 对称 \(\Rightarrow\) A 内积对称

\[ (v,w)_{A}=\big((v,w)_{A}\big)^{T}=(v^{T}Aw)^{T}=w^{T}A^{T}v=w^{T}Av=(w,v)_{A} \]

共轭梯度方法

  • 直接方法，通过有限步得到解

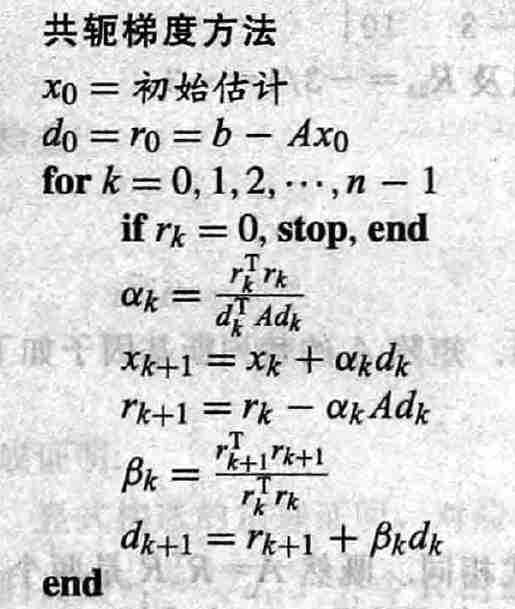
  • 每次更新 \(x_k,d_{k},r_{k}\) 这 3 个向量
    • \(x_{k}\)：近似解
    • \(r_{k}\)：近似解 \(x_k\) 的余项
    • \(d_k\)：搜索方向
  • \(\alpha_k,\beta_k\)：实数，临时变量

算法解释

定理与证明

  • 注：红框部分应该是 \(r_{k}^{T}Ad_{k}\)

对比

  • 共轭梯度方法计算代价大致在 \(n^3\)，比高斯消去大
  • 共轭梯度方法代码实现上比高斯消去更简单，没有一些边界需要处理
  • 对于病态矩阵，共轭梯度方法比部分主元的高斯消去效果更差，可以通过预条件处理进行缓解
  • 后向误差和余项的欧几里得长度，随着每一步下降，因而至少对于这种度量方式，\(Ax_i\) 在每一步变得和 \(b\) 越来越接近。因而通过检测 \(r_i\)，可能得到一个足够好的 \(x\)，并不必做完 \(n\) 步，在这种情况下，共轭梯度方法和迭代方法没有区别。

6.4 预条件

  • 思想：降低问题中的条件数
  • \(Ax=b\) 的预条件形式 \(M^{-1}Ax=M^{-1}b\)
  • 矩阵 \(M\) 应该满足如下条件
    • 足够接近 \(A\)
    • 求逆足够简单
  • 这俩条件常常矛盾
    • \(M=A\) 时，方程变为 \(x=A^{-1}b\)，条件数为 1，但是 \(A\) 不容易求逆
    • \(M=I\) 是，方程变为 \(Ax=b\)，不能降低条件数

雅可比预条件子

  • \(D\) 是 \(A\) 的对角线矩阵
  • \(D\) 的逆矩阵也是对角线矩阵，刚好为 \(D\) 中对应元素的倒数
  • 在严格对角占优矩阵 \(A\) 中，\(D\) 与 \(A\) 相似且容易求逆

预条件子的共轭梯度算法

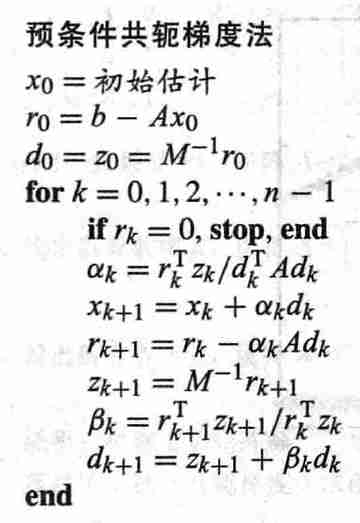
说明

高斯-塞德尔预条件子

\[ \begin{aligned} \begin{array}{c} ... \end{array} \end{aligned} \]

7. 非线性方程组

7.1 多元牛顿方法

  • 多元非线性方程组

\[ \left\{ \begin{array}{l} f_{1}(u,v,w)=0\\ f_{2}(u,v,w)=0\\ f_{3}(u,v,w)=0\\ \end{array} \right. \]

  • 向量值函数

\[ F(x)=(f_1,f_2,f_3) \]

  • 多元非线性方程组转化为

\[ F(x)=0,x=(u,v,w) \]

  • 雅可比矩阵

\[ DF(x)=\begin{pmatrix} \dfrac{\partial{f_1}}{\partial{u}}&\dfrac{\partial{f_1}}{\partial{v}}&\dfrac{\partial{f_1}}{\partial{w}}\\ \dfrac{\partial{f_2}}{\partial{u}}&\dfrac{\partial{f_2}}{\partial{v}}&\dfrac{\partial{f_2}}{\partial{w}}\\ \dfrac{\partial{f_3}}{\partial{u}}&\dfrac{\partial{f_3}}{\partial{v}}&\dfrac{\partial{f_3}}{\partial{w}}\\ \end{pmatrix} \]

  • \(F(x)\) 在 \(x_0\) 附近的泰勒展开
    • 每一行对应一个多元函数的泰勒展开

\[ \begin{align} F(x)&=F(x_0)+DF(x_0)(x-x_0)+O(x-x_0)^2\\ &\approx F(x_0)+DF(x_0)(x-x_0)\\ \end{align} \]

  • 多变量牛顿方法

\[ 0=F(r)=F(x_0)+DF(x_0)(r-x_0) \]

多变量牛顿方法

\[ \begin{aligned} \begin{array}{l} x_0=初始估计向量\\ x_{k+1}=x_{k}-\big(DF(x_k)\big)^{-1}F(x_k)\\ \end{array} \end{aligned} \]

  • 利用高斯消去（\(\dfrac{n^2}{3}\)）替代矩阵求逆（\(n^3\)）

\[ \begin{array}{c} DF(x_k)s=-F(x_k)\\ x_{k+1}=x_{k}+s\\ \end{array} \]

7.2 Broyden 方法

  • 如果雅可比矩阵不好计算怎么办？
    • 得同时更新雅可比矩阵
  • 看不懂了

  • 如果没有更好的选择，初始的雅可比矩阵可以使用单位阵

Broyden 算法

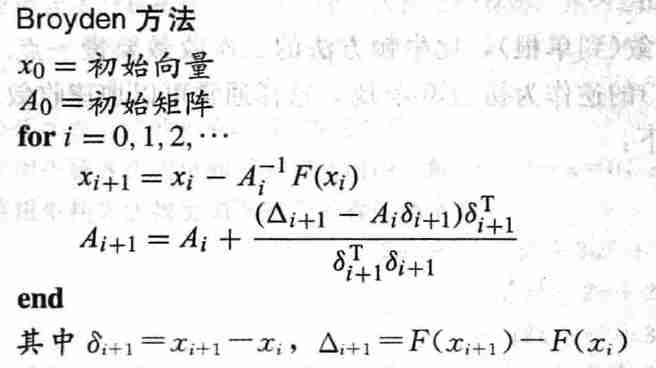
Broyden 算法 II

  • 避免矩阵求解步骤 \(A_i\delta_{i+1}=-F(x_i)\)
  • 直接近似 \(DF\) 的逆，而不是近似 \(DF\)
  • 令 \(B_i=A_i^{-1}\)

  • 算法