计算方法B.裴玉茹.03.方程组(2)
- 数值分析课本第 2 章(方程组) + PPT(非线性方程组迭代求解)
方程组
4. PA-LU 分解
- 之前朴素高斯法的问题:0主元 + 淹没
- 改进策略:交换矩阵的行
- 部分主元
4.1 部分主元
- 我们进行对主元 \(a_{ii}\) 的操作时, 在进行高斯消去之前,我们找到剩余行 \((i\le p\le n)\) 中第 \(i\) 列中的绝对值最大值 \(a_{pi}\) ,将该行和第 \(i\) 行进行交换,然后再进行高斯消去
- 此时保证每次进行操作的主元嗾使剩余行中的最大值,避免了上面的0主元和淹没问题
- 淹没:保证所有乘子三维绝对值小于 1
- 0主元:如果全为 0,则为奇异矩阵,高斯消去方法无法求解
4.2 置换矩阵
- 置换矩阵,每一行每一列有且仅有一个 1,其余全为 0
- 置换矩阵左乘一个矩阵
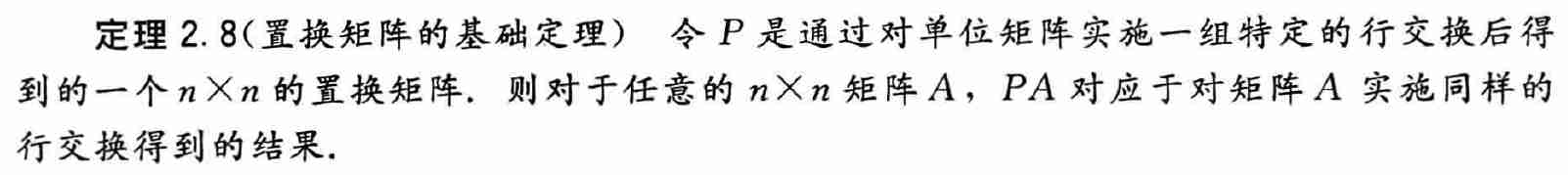
4.3 PA=LU 分解
一个例子

例子分析
- 通过上面的例子,我们形式化的将 4 个矩阵,\(P,A,L,U\),形式化的定义出来,从而证明上面算法的正确性
- 下标从 1 开始
- 记针对主元 \(a_{ii}\) 的换行操作为 \(P_{i}\),针对主元 \(a_{ii}\) 消去第 \(j\) 行的操作为 \(L_{ij}\)
- 根据上面的算法流程,可以得到如下一系列式子
\[ \begin{array}{c} L_{23}P_{2}L_{13}L_{12}P_{1}A=U\\ P=P_{2}P_{1}\\ \end{array} \]
- 对于矩阵 \(L\),他对于 \(I\) 矩阵的影响如下
- 注意对于 \(L\) 矩阵,左下角的矩阵中的值生成之后就不再改变
- 这里用到了之前的定理
\[ LI=P_{2}\left(L_{12}^{-1}L_{13}^{-1}{\color{red}P_{1}}I{\color{red}P_{1}^{-1}}\right)P_{2}^{-1}L_{23}^{-1} \]
- 我们记 \(L_{13}^{-1}L_{12}^{-1}P_{1}IP_{1}^{-1}=L_{1}\),也就是经过对主元 \(a_{11}\) 处理完之后的 \(L\) 矩阵
- 分析 \(P_{1}L_{1}P_{1}^{-1}\)
这一步的操作(以上面的例子为例)
- 我们在计算中做的操作实际上就是将矩阵 \(L_{1}\) 左下角的部分第 \(2,3\) 行做了交换
- 实际上的矩阵操作就是我们先将第 \(2,3\) 行互换,然后再将第 \(2,3\) 列互换
- \(P_{1}^{-1}=P_{1}\)(这里的 \(P_{i}\) 都是只对单位矩阵做一次行变换的结果)
- 左乘交换矩阵就是行变换、右乘交换矩阵就是列变换
- 注意我们在操作主元 \(a_{ii}\) 时,第 \(i\) 列(含 \(i\))之后的元素都还未处理,因此交换 \(i,j\) 列影响的本质上只有两个 \(1\)
- 实际效果如下
\[ \begin{bmatrix} 1 & 0 & 0\\ \dfrac{1}{2} & 1 & 0\\ \dfrac{1}{4} & 0 & 1\\ \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 0 & 0\\ \dfrac{1}{4} & 1 & 0\\ \dfrac{1}{2} & 0 & 1\\ \end{bmatrix} \]
- 我们验证
\[ \begin{aligned} LU&=P_{2}L_{12}^{-1}L_{13}^{-1}P_{1}IP_{1}^{-1}P_{2}^{-1}L_{23}^{-1}L_{23}P_{2}L_{13}L_{12}P_{1}A\\ &=P_{2}P_{1}A\\ &=PA \end{aligned} \]
- 对于 \(n\times n\) 的矩阵,我们有
\[ L_i= \left\{ \begin{array}{ll} P_{i}L_{i-1}P_{i}^{-1}L_{i,i+1}\cdots L_{i,n}&,i>0\\ I&,i=0 \end{array} \right. \]
\[ U_i= \left\{ \begin{array}{ll} L_{i,n}^{-1}\cdots L_{i,i+1}^{-1}P_{i}U_{i-1}&,i>0\\ A&,i=0 \end{array} \right. \]
- 于是有
\[ L_iU_i= \left\{ \begin{array}{ll} P_{i}L_{i-1}P_{i}^{-1}L_{i,i+1}\cdots L_{i,n}L_{i,n}^{-1}\cdots L_{i,i+1}^{-1}P_{i}U_{i-1}=P_{i}L_{i-1}U_{i-1}&,i>0\\ A&,i=0 \end{array} \right. \]
- 那么成立 \(PA=LU\)
\[ LU=L_{n-1}U_{n-1}=P_{n-1}L_{n-2}U_{n-2}=\cdots=P_{n-1}\cdots P_{1}A=PA \]
5. 迭代方法
5.1 雅可比方法
- Jacobi 方法
- 求解第 \(i\) 个方程得到第 \(i\) 个未知量,然后使用不动点迭代方法
- 对如下方程组使用雅可比方法
\[ \left\{ \begin{array}{c} 3u+v=5\\ u+2v=5\\ \end{array} \right. \Rightarrow \left\{ \begin{array}{c} u=\dfrac{5-v}{3}\\ v=\dfrac{5-u}{2}\\ \end{array} \right. \]
- 根据初始估计进行迭代,收敛至正确结果
\[ \begin{array}{c} (u_0,v_0)=(0,0)\\ (u_1,v_1)=(\dfrac{5}{3},\dfrac{5}{2})\\ \cdots\\ (u_n,v_n)=(1,2)\\ \end{array} \]
- 换一种方法则发散
\[ \left\{ \begin{array}{c} v=5-3u\\ u=5-2v\\ \end{array} \right. \]
严格对角占优矩阵

定理 2.10

- 注意这只是个充分条件
满秩证明
- 假设不满秩,则存在非零向量 \(x=(x_1,\cdots,x_n)^T\) 使得 \(Ax=0\) 成立
- 假设 \(\vert{x_k}\vert\ge\vert{x_i}\vert,\forall i\),那么有 \(\vert{x_{k}}\vert\ge0\)
- 那么有
\[ 0=\sum_{j=1}^{n}a_{kj}x_{j} \]
\[ \left\vert{\sum_{j\ne k}a_{kj}x_{j}}\right\vert=\vert{-a_{kk}x_k}\vert=\vert{a_{kk}}\vert\vert{x_k}\vert>{\sum_{j\ne k}\vert{a_{kj}}\vert\vert{x_{j}}\vert}\ge\left\vert{\sum_{j\ne k}a_{kj}x_{j}}\right\vert \]
- 矛盾,因此满秩
雅可比方法
- \(A=L+D+U\)
- 矩阵 = 下三角矩阵(对角线为 0) + 主对角线矩阵 + 上三角矩阵(对角线为 0)
\[ \begin{array}{c} Ax=b\\ (L+D+U)x=b\\ Dx=b-(L+U)x\\ x=D^{-1}\big(b-(L+U)x\big) \end{array} \]
- 雅可比方法
\[ \begin{array}{l} x_0=初始估计\\ x_{k+1}=D^{-1}\big(b-(L+U)x_{k}\big)\\ \end{array} \]
5.2 高斯-赛德尔方法和 SOR
Guass-Seidel 方法
- 在雅可比方法的基础上,在第 \(k\) 轮迭代的时候,如果某一个 \(x\) 的 \(x_k\) 已经被计算出来,则使用 \(x_k\) 进行迭代,而不是 \(x_{k-1}\)
\[ \begin{array}{l} x_0=初始估计\\ x_{k+1}=D^{-1}\big(b-Lx_{k+1}-Ux_{k}\big)\\ \end{array} \]
- 例子
\[ \begin{bmatrix} 3 & 1 & -1\\ 2 & 4 & 1\\ -1 & 2 & 5\\ \end{bmatrix} \begin{bmatrix} u\\ v\\ w\\ \end{bmatrix} = \begin{bmatrix} 4\\ 1\\ 1\\ \end{bmatrix} \]
- 高斯赛德尔迭代
\[ \left\{ \begin{array}{c} u_{k+1}=\dfrac{4-v_{k}+w_{k}}{3}\\ v_{k+1}=\dfrac{1-2u_{k+1}-w_{k}}{4}\\ w_{k+1}=\dfrac{1+u_{k+1}-2v_{k+1}}{5}\\ \end{array} \right. \]
SOR
- SOR:连续过松弛方法

- 上面的例子
\[ \left\{ \begin{array}{l} u_{k+1}=(1-\omega)u_{k}+\omega\times\dfrac{4-v_{k}+w_{k}}{3}\\ v_{k+1}=(1-\omega)v_{k}+\omega\times\dfrac{1-2u_{k+1}-w_{k}}{4}\\ w_{k+1}=(1-\omega)w_{k}+\omega\times\dfrac{1+u_{k+1}-2v_{k+1}}{5}\\ \end{array} \right. \]
- 也可以如此理解
\[ \begin{array}{c} Ax=b\\ \omega Ax=\omega b\\ \omega(L+D+U)x=\omega b\\ (\omega L+D)x=\omega b+(1-\omega)Dx-\omega Ux\\ x=(\omega L+D)^{-1}\big(\omega b+(1-\omega)Dx-\omega Ux\big)\\ x=(\omega L+D)^{-1}\big((1-\omega)Dx-\omega Ux\big)+\omega(\omega L+D)^{-1}b\\ \end{array} \]
- SOR
\[ \begin{array}{l} x_0=初始估计\\ x_{k+1}=(\omega L+D)^{-1}\big((1-\omega)D-\omega U\big)x_{k}+\omega(\omega L+D)^{-1}b\\ \end{array} \]
- \(\omega=1\):高斯赛德尔方法
- \(\omega<1\):连续欠松弛方法
5.3 迭代方法的收敛
谱半径

雅可比方法的收敛性
- 定理 2.10
- 雅可比方法
\[ x_{k+1}=-D^{-1}(L+U)x_{k}+D^{-1}b\\ \]
我们记 \(R=L+U\),则需要证明 \(\rho(D^{-1}R)<1\)
我们取矩阵 \(D^{-1}R\) 特征值 \(\lambda\) 和其对应的特征向量 \(v\),让 \(v\) 对其绝对值最大的元素归一化,使其满足 \(\Vert{v}\Vert_{\infty}=1\)
- 不妨设 \(v_{m}=1\)
\[ D^{-1}Rv=\lambda v\Leftrightarrow Rv=D\lambda v \]
- \(r_{mm}=0\)(对角线元素全为 0)
- \(D\) 是对角矩阵
\[ \left\vert{\sum_{i=1}^{n}r_{mi}v_i}\right\vert=\left\vert{\sum_{i\ne m}r_{mi}v_i}\right\vert=\left\vert{\sum_{i=1}^{n}\lambda d_{mi}v_{i}}\right\vert=\left\vert{\lambda d_{mm}v_{m}}\right\vert=\vert{\lambda}\vert\vert{d_{mm}}\vert \]
- 那么有
\[ \left\vert{\sum_{i\ne m}r_{mi}v_i}\right\vert<\sum_{i\ne m}\left\vert{r_{mi}v_i}\right\vert<\sum_{i\ne m}\left\vert{r_{mi}}\right\vert<\vert{d_{mm}}\vert\Rightarrow\lambda<1 \]
- 因此收敛,于是对应任意的 \(b\),\(Ax=b\) 都有唯一解, \(A\) 是非奇异矩阵
高斯赛德尔方法的收敛性

- 高斯赛德尔方法
\[ x_{k+1}=-(L+D)^{-1}Ux_{k}-(L+D)^{-1}b \]
- 类似的
\[ (L+D)^{-1}Uv=\lambda v\Leftrightarrow Uv=\lambda(L+D)v \]
- 第 \(m\) 行
\[ \left\vert{\sum_{i=1}^{n}a_{mi}v_i}\right\vert =\left\vert{\sum_{i>m}a_{mi}v_i}\right\vert =\left\vert{\sum_{i\le m}\lambda a_{mi}v_i}\right\vert \]
- 于是有
\[ \begin{aligned} \vert{\lambda}\vert\sum_{i>m}\vert{a_{mi}}\vert &<\vert{\lambda}\vert \left(\vert{a_{mm}}\vert-\sum_{i<m}\vert{a_{mi}}\vert\right) \le\vert{\lambda}\vert \left(\vert{a_{mm}}\vert-\sum_{i<m}\vert{a_{mi}v_i}\vert\right)\\ &\le\vert{\lambda}\vert \left\vert{a_{mm}}+\sum_{i<m}{a_{mi}v_i}\right\vert =\left\vert{\lambda}\sum_{i\le m}{a_{mi}v_i}\right\vert =\left\vert{\sum_{i>m}a_{mi}v_i}\right\vert\\ &\le\left\vert{\sum_{i>m}a_{mi}}\right\vert \le\sum_{i>m}\left\vert{a_{mi}}\right\vert \end{aligned} \]
- 推出 \(\lambda<1\)
5.4 稀疏矩阵计算
- 迭代方法的好处
- 如果有近似解,则迭代方法可以更快
- 修饰:利用之前相关问题得到近似解作为初始估计,进而求解
- 稀疏矩阵求解
- 高斯消去的方法,很可能会将原来的稀疏矩阵进行填充,问题复杂化
- 如果有近似解,则迭代方法可以更快