普吕克坐标(Plücker Coordinates) 简介
普吕克坐标
- Plücker Coordinates
- 3 维欧氏空间的一条直线被两个其上不同的点确定,或者被两个包含这条直线的平面确定
几何定义
两个点导出
- 直线 \(L\),考虑 \(L\) 上两个不同的点:\(x=(x_{1},x_{2},x_{3}),y=(y_{1},y_{2},y_{3})\)
- \(d=y-x\)
- 矩:\(m={x}\times{y}\)
- 质点从 \(x\) 移动到 \(y\) 的矩
- \(m\) 的大小为三角形 \(Oxy\) 面积的两倍,正比于 \(d\) 的大小
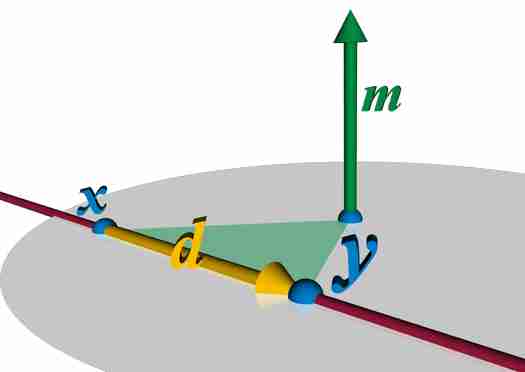
- \({d}\cdot{m}=0\)
- 垂直
- 单独 \(d\) 或者 \(m\) 都无法唯一确定直线 \(L\),他们俩才能唯一确定直线 \(L\)
- 定义齐次坐标如下
\[ (d:m)=(d_1:d_2:d_3:m_1:m_2:m_3) \]
- 其中
\[ \begin{aligned} \begin{array}{c} d_1=y_1-x_1\\ d_2=y_2-x_2\\ d_3=y_3-x_3\\ m_1=x_2y_3-y_2x_3\\ m_2=x_3y_1-y_3x_1\\ m_3=x_1y_2-y_1x_2\\ \end{array} \end{aligned} \]
- 所有的 \((\lambda d:\lambda m),\lambda\ne0\) 都可以由直线 \(L\) 上不同的两个点生成
- \((d:m)\) 就是普吕克坐标
代数定义
- 直线 \(L\) 穿过两个点 \(x,y\),他们的齐次坐标表示为 \(x=(x_0,x_1,x_2,x_3),y=(y_0,y_1,y_2,y_3)\)
- 坐标 0 为其次项
- 定义普吕克坐标为 \(p_{ij}=x_iy_j-x_jy_i\)
- \(p_{ii}=0,p_{ij}=-p_{ji}\)
- 因此只有 6 个独立变量,对应普吕克坐标
\[ (p_{01}:p_{02}:p_{03}:p_{23}:p_{31}:p_{12}) \]
线线相交
- 3 维欧氏空间中,两条直线 \(L,L'\) 相交则有
\[ d\cdot m'+m\cdot d=0 \]
- 其中 \(p_{ij},p_{ij}'\) 是 \(L,L'\) 的普吕克矩阵
\[ \begin{aligned} 0&=p_{01}p'_{23}+p_{02}p'_{31}+p_{03}p'_{12}+p_{23}p'_{01}+p_{31}p'_{02}+p_{12}p'_{03}\\ &= \begin{vmatrix} x_{0}&y_{0}&x'_{0}&y'_{0}\\ x_{1}&y_{1}&x'_{1}&y'_{1}\\ x_{2}&y_{2}&x'_{2}&y'_{2}\\ x_{3}&y_{3}&x'_{3}&y'_{3} \end{vmatrix} \end{aligned} \]
- 如果不相交,上面式子的正负表示方向
- 正:\(L\) 为大拇指,\(L'\) 的方向为右手螺旋
- 负:\(L\) 为大拇指,\(L'\) 的方向为左手螺旋
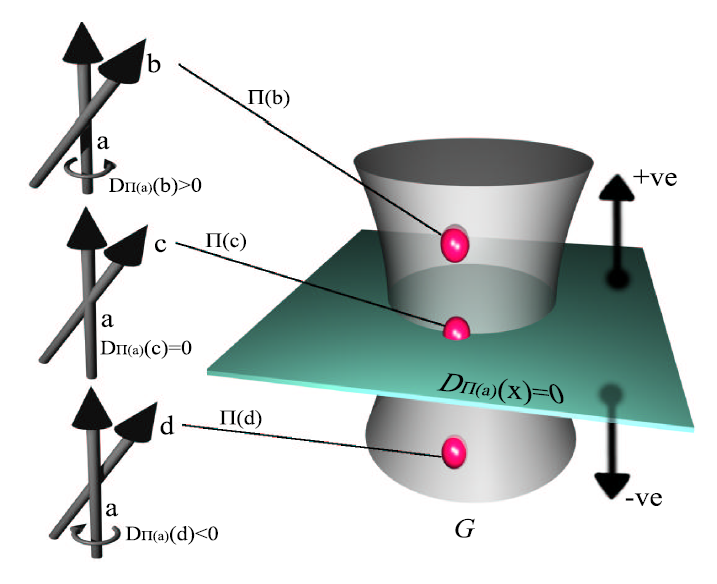
齐次坐标行列式为 0
二维平面
- \(A(x_a,y_a),B(x_b,y_b),C(x_c,y_c)\) 三点共线 等价于这三个点的齐次坐标组成的行列式值为 0
\[ \begin{vmatrix} x_{a}&x_{b}&x_{c}\\ y_{a}&y_{b}&y_{c}\\ 1&1&1\\ \end{vmatrix} \]
- \(\vec{AB}=k\cdot\vec{AC}\)
- 齐次项化为 1 之后,再相减,此时第三维为 0
- 说明线性相关,行列式为 0
三维平面
- 类似的,首先将齐次项化为 1,通过同时减去某一列,判断其是否线性相关即可
\[ \begin{vmatrix} x_{0}&y_{0}&x'_{0}&y'_{0}\\ x_{1}&y_{1}&x'_{1}&y'_{1}\\ x_{2}&y_{2}&x'_{2}&y'_{2}\\ x_{3}&y_{3}&x'_{3}&y'_{3} \end{vmatrix} \]
- \(\vec{AB}=k_1\cdot\vec{AC}+k_2\cdot\vec{AD}\)