计算方法B.裴玉茹.03.方程组
- 数值分析课本第 2 章(方程组) + PPT(非线性方程组迭代求解)
方程组
1. 高斯消去法
1.1 朴素的高斯消去法
- 等价变化(行列式变换)
- 两个方程彼此交换位置
- 在一个方程上加上或者减去两外一个方程的倍数
- 对于一个方程乘上一个非零的常数
- 步骤
- 化为上三角阵
- 回代(后向求解)
1.2 操作次数
\[ 1+2+\cdots+n=\dfrac{n(n+1)}{2} \]
\[ 1^2+2^2+\cdots+n^2=\dfrac{n(n+1)(2n+1)}{6} \]
- 输入的方程组(含有 n 个未知数的 n 个方程组)

把矩阵的下三角部分转化为全 0
- 例如消去 \(a_{21}\),对第二列作如下操作
\[ a_{21}-\dfrac{a_{21}}{a_{11}}a_{11} \]
- 对于这一行:1个除法 + n 个乘法 + n 个减法
- 第一列不用,但是 \(b_i\) 也要做同样的计算
\(a_{ii}\) 会在分母中出现,被称为是主元,上面的操作要求 \(a_{ii}\) 不为 0
我们可以计算得到消去这一步中的操作次数
\[ \sum_{k=n}^{1}(2k+1)(k-1)=\dfrac{4n^3+3n^2-7n}{6} \]
- 此时方程转化为

- 此时只需要从下到上一步步回代即可
- 1 除法、(n-i) 乘法、(n-i) 减法
\[ x_{i}=\dfrac{b_i-a_{i,i+1}x_{i+1}-\cdots-a_{i,n}x_{n}}{a_{ii}} \]
- 操作次数
\[ \sum_{i=1}^{n}2(n-i)+1=\sum_{i=1}^{n}2(i-1)+1=n^2 \]
- 高斯消去法时间复杂度:\(O(n^3)\)
- 消去:\(O(n^3)\)
- 回代:\(O(n^2)\)
2. LU 分解
2.1 高斯消去法的矩阵形式
- Ax=B
- LU 分解是高斯消去法的矩阵形式
- L:下三角矩阵
- U:上三角矩阵
- 如下几个事实支持 LU 分解
事实1
- 矩阵左乘相当于高斯消去法的变换

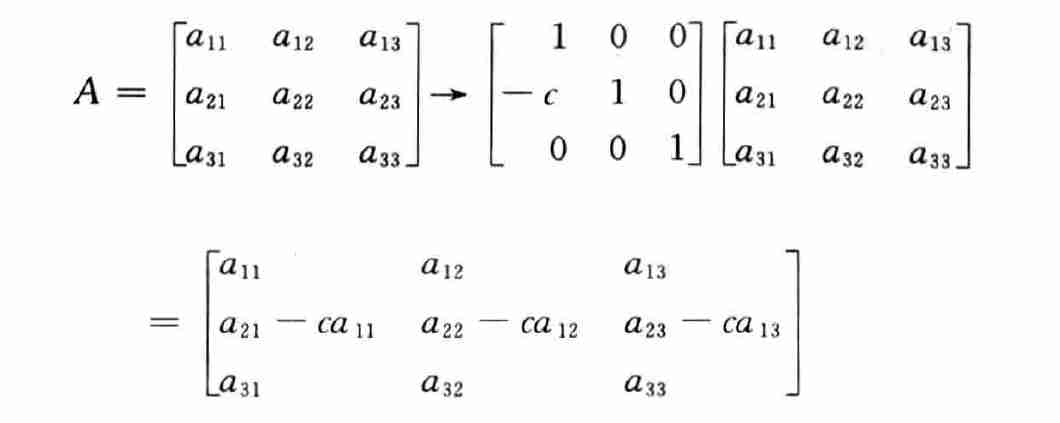
事实2
- 逆就是取反
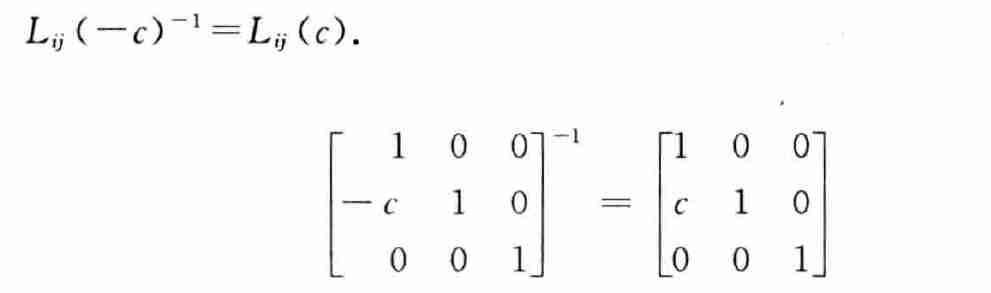
事实3
- 相乘得到结果(注意顺序)
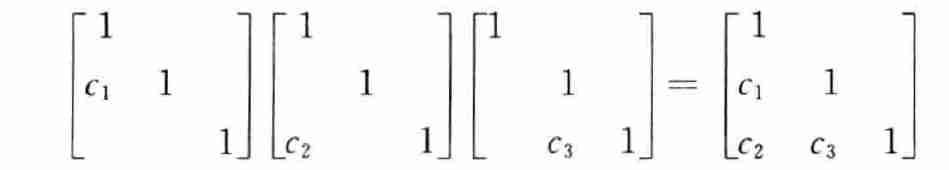
结论
- 原来的矩阵通过高斯变换转化为上三角矩阵
- \(A\) 通过若干 \(L_{ij}\) 的变换得到 \(U\)
- 将若干变换记作 \(L^{-1}\)
- \(L^{-1}A = U\Rightarrow A=LU\)
2.2 使用 LU 分解回代
- \(Ax=b\Rightarrow LUx=b\)
- 记 \(Ux=c\),有 \(Lc=b\)
- 回代过程如下
- 通过 \(Lc=b\),解出 \(c\)
- 通过 \(Ux=c\),解出 \(x\)
2.3 LU 分解的复杂度
LU 分解的好处
- 如果对于一系列的方程组求解
\[ \begin{aligned} \begin{array}{c} Ax=b_1\\ Ax=b_2\\ \cdots\\ Ax=b_k\\ \end{array} \end{aligned} \]
- 对于原始的高斯消去法,每次都需要经过复杂的消去操作
- 复杂度约为:\(\dfrac{2kn^3}{3}\)
- 但是对于 LU 分解方法,消去操作只需要做一次
- 复杂度约为:\(\dfrac{2n^3}{3}+2kn^2\)

- 并不是所有的矩阵都能进行 LU 分解
实际实现
- 知乎参考
- 注意一些性质
- L 对角线为 1,下三角阵
- R 上三角阵
\[ {A_{ij}}= \left\{ \matrix{ \sum\limits_{k = 1}^i L_{ik}U_{kj} ,(i < j)\\ \sum\limits_{k = 1}^j L_{ik}U_{kj} ,(i > j)\\ \sum\limits_{k = 1}^i L_{ik}U_{kj} ,(i = j)\\ }\right. \Rightarrow \left\{ \matrix{ \sum\limits_{k = 1}^{i - 1} L_{ik}U_{kj} + U_{ij} = A_{ij},(i \le j)\\ \sum\limits_{k = 1}^{j - 1} L_{ik}U_{kj} + L_{ij}U_{jj} = A_{ij},(i > j)\\ }\right. \]
\[ \Rightarrow \left\{ \matrix{ U_{ij} = A_{ij} - \sum\limits_{k = 1}^{i - 1} L_{ik}U_{kj} ,(i \le j)\\ L_{ij} = \dfrac{A_{ij}-\sum\limits_{k = 1}^{j - 1} L_{ik}U_{kj}}{U_{jj}},(i > j)\\ }\right. \]
- 先计算 \(U_{ij}\),再计算 \(L_{ij}\)
3. 误差来源
- 病态矩阵
- 淹没
3.1 误差放大和条件数
- 无穷范数
- 向量 \(x=(x_1,\cdots,x_n)\) 的无穷范数为 \(\Vert{x}\Vert_{\infty}=\max\vert{x_i}\vert\)
- \(x_a\) 是线性方程组 \(Ax=b\) 的近似解
- 余项:\(r=b-Ax_a\)
- 后向误差:\(\Vert{b-Ax_a}\Vert_{\infty}\)
- 前向误差:\(\Vert{x-x_a}\Vert_{\infty}\)
- 前向误差和后向误差可能有不同数量级
- 大的前向误差、小的后向误差
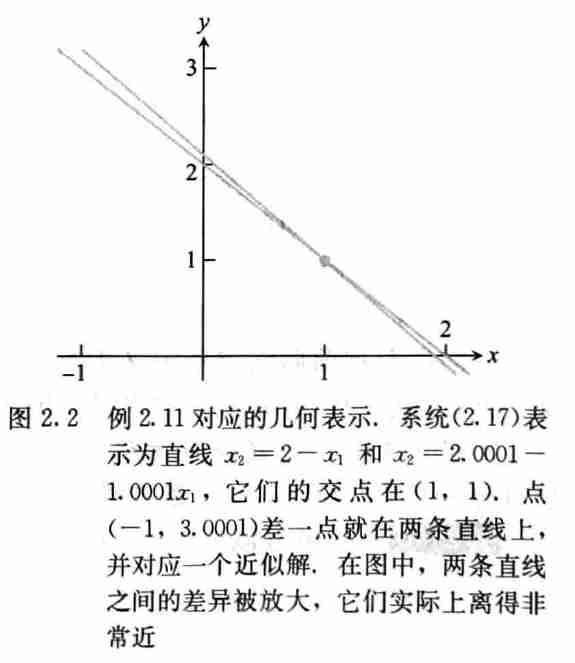
- 相对前向误差
\[ \dfrac{\Vert{x-x_a}\Vert_{\infty}}{\Vert{x}\Vert_{\infty}} \]
- 相对后向误差
\[ \dfrac{\Vert{b-Ax_a}\Vert_{\infty}}{\Vert{b}\Vert_{\infty}}=\dfrac{\Vert{r}\Vert_{\infty}}{\Vert{b}\Vert_{\infty}} \]
- 误差放大因子
\[ 误差放大因子=\dfrac{相对前向误差}{相对后向误差}=\dfrac{\dfrac{\Vert{x-x_a}\Vert_{\infty}}{\Vert{x}\Vert_{\infty}}}{\dfrac{\Vert{r}\Vert_{\infty}}{\Vert{b}\Vert_{\infty}}} \]
- 条件数
- 在预先定义的输入误差范围中最大的误差放大倍数
条件数
- 方阵 A 的条件数 cond(A) 为求解 Ax=b 时,对于所有的右侧向量 b,可能出现的最大误差放大因子
- 矩阵范数
- \(n\times n\) 矩阵 A 的矩阵范数定义如下
- 每行元素绝对值之和的最大值
\[ \Vert{A}\Vert_{\infty}=\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right) \]
- \(n\times n\) 矩阵的 A 的条件数是(这里指的是算子范数)
\[ \mathrm{cond}(A)=\Vert{A}\Vert\cdot\Vert{A^{-1}}\Vert \]
精度丢失
- 相对后向误差不可能小于 \(\epsilon_{\mathrm{mach}}\),因此相对前向误差可能达到
\(\epsilon_{\mathrm{mach}}\cdot
\mathrm{cond}(A)\) 这么大
- 也就是说如果我们 \(\mathrm{cond}(A)\approx{10^k}\),在计算 Ax=b 时可能丢掉 k 位数字精度
向量范数

1-范数
- n 维向量的1-范数
\[ \Vert{x}\Vert_{1}=\vert{x_1}\vert+\vert{x_2}\vert+\cdots+\vert{x_n}\vert \]
- \(n\times n\) 矩阵 A 的 1-范数
- 最大绝对列和
- 列向量的 1-范数 的最大值
\[ \Vert{A}\Vert_{1}=\max_{j}\left(\sum_{i=1}^{n}\vert{a_{ij}}\vert\right) \]
算子范数
- 矩阵范数使用特定的向量范数定义
\[ \Vert{A}\Vert=\max\dfrac{\Vert{Ax}\Vert}{\Vert{x}\Vert} \]
- 矩阵1-范数是向量1-范数的算子范数
1-范数证明
\[ \begin{aligned} L&=\max\dfrac{\Vert{Ax}\Vert_1}{\Vert{x}\Vert_1}\\ R&=\max_{j}\left(\sum_{i=1}^{n}\vert{a_{ij}}\vert\right)\\ \end{aligned} \]
- 思路:\(L\le R,L\ge R\)
\(L\le R\)
\[ \begin{aligned} {\Vert{Ax}\Vert_1}=&\sum_{i=1}^{n}\left\vert\sum_{j=1}^{n}a_{ij}x_j\right\vert\\ \le&\sum_{i=1}^{n}\sum_{j=1}^{n}\vert a_{ij}\vert\vert x_j\vert\\ =&\sum_{j=1}^{n}\sum_{i=1}^{n}\vert a_{ij}\vert\vert x_j\vert\\ =&\sum_{j=1}^{n}\left(\vert x_j\vert\sum_{i=1}^{n}\vert a_{ij}\vert\right)\\ \le&\sum_{j=1}^{n}\left(\vert x_j\vert\max_{j}{\sum_{i=1}^{n}\vert a_{ij}\vert}\right)\\ =&\max_{j}{\sum_{i=1}^{n}\vert a_{ij}\vert}\cdot\sum_{j=1}^{n}\vert x_j\vert\\ =&\max_{j}{\sum_{i=1}^{n}\vert a_{ij}\vert}\cdot\Vert{x}\Vert_1 \end{aligned} \]
\(L\ge R\) 构造
- 构造 \(\lambda\) 如下,\(\lambda=R\)
\[ \lambda=\sum_{i=1}^{n}{\vert{a_{is}}\vert}=\max_{j}\sum_{i=1}^{n}{\vert{a_{ij}}\vert},1\le{s}\le{n} \]
- 记 \(A=\left(\alpha_1,\cdots,\alpha_n\right)\)
- 设 n 维向量 \(\epsilon_{s}\) 如下,除了第 s 维为 1,其余都为 0
\[ \epsilon_{s}={(0,0,\cdots,0,1,0,\cdots,0)}^{T} \]
- 那么有
\[ {\Vert{A\epsilon_s}\Vert_1}={\Vert{\alpha_s}\Vert_1}=\lambda=\lambda\Vert{\epsilon_s}\Vert \]
\[ \Rightarrow\dfrac{\Vert{A\epsilon_s}\Vert_1}{\Vert{\epsilon_s}\Vert_1}=\lambda \]
- 于是
\[ L=\max\dfrac{\Vert{Ax}\Vert_1}{\Vert{x}\Vert_1}\ge\dfrac{\Vert{A\epsilon_s}\Vert_1}{\Vert{\epsilon_s}\Vert_1}=\lambda=R \]
无穷范数证明
\[ \begin{aligned} L&=\max\dfrac{\Vert{Ax}\Vert_\infty}{\Vert{x}\Vert_\infty}\\ R&=\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right)\\ \end{aligned} \]
\(L\le R\)
\[ \begin{aligned} {\Vert{Ax}\Vert_\infty}=&\max_{i}\left\vert\sum_{j=1}^{n}a_{ij}x_j\right\vert\\ \le&\max_{i}\sum_{j=1}^{n}\vert a_{ij}\vert\vert x_j\vert\\ \le&\max_{i}\left(\sum_{j=1}^{n}\vert a_{ij}\vert\max_{k}{\vert x_k\vert}\right)\\ \le&\max_{k}{\vert x_k\vert}\cdot\max_{i}\left(\sum_{j=1}^{n}\vert a_{ij}\vert\right)\\ =&{\Vert{x}\Vert_\infty}\cdot\max_{i}\left(\sum_{j=1}^{n}\vert a_{ij}\vert\right)\\ \end{aligned} \]
\(L\ge R\) 构造
- \(e^{i\theta}=\cos\theta+i\sin\theta\)
- 设 \(\mu\) 如下,\(\mu=R\)
\[ \mu=\sum_{j=1}^{n}\vert{a_{sj}}\vert=\max_{i}\left(\sum_{j=1}^{n}\vert{a_{ij}}\vert\right) \]
- 记 \(A=\left(\alpha_1,\cdots,\alpha_n\right)\)
- 记 \(a_{ij}=\vert{a_{ij}}\vert e^{i\theta_j}\)
- 设 n 维向量 \(z\) 如下
\[ z=(e^{-s\theta_1},\cdots,e^{-s\theta_n})\Rightarrow\Vert{z}\Vert_\infty=1 \]
- 那么有
- \(\sum_{j=1}^{n}{\vert{a_{ij}}\vert}e^{i\theta_j}e^{-s\theta_j}\le\sum_{j=1}^{n}{\vert{a_{ij}}\vert}\le{\sum_{j=1}^{n}{\vert{a_{sj}}\vert}}\)
- \(e^{i\theta_j}e^{-s\theta_j}\le1\),等号在 \(i=s\) 的时候取到
- \({\sum_{j=1}^{n}{\vert{a_{ij}}\vert}}\le{\sum_{j=1}^{n}{\vert{a_{sj}}\vert}}\),等号在 \(i=s\) 的时候取到
- 同时,\(\sum_{j=1}^{n}{\vert{a_{ij}}\vert}e^{i\theta_j}e^{-s\theta_j}\ge-\sum_{j=1}^{n}{\vert{a_{ij}}\vert}\ge-{\sum_{j=1}^{n}{\vert{a_{sj}}\vert}}\)
- \(\sum_{j=1}^{n}{\vert{a_{ij}}\vert}e^{i\theta_j}e^{-s\theta_j}\le\sum_{j=1}^{n}{\vert{a_{ij}}\vert}\le{\sum_{j=1}^{n}{\vert{a_{sj}}\vert}}\)
\[ {\Vert{Az}\Vert_\infty}=\max_{i}\left\vert{\sum_{j=1}^{n}{\vert{a_{ij}}\vert}e^{i\theta_j}e^{-s\theta_j}}\right\vert=\left\vert{\sum_{j=1}^{n}{\vert{a_{sj}}\vert}}\right\vert=\mu=\mu\Vert{z}\Vert_\infty \]
\[ \Rightarrow\dfrac{\Vert{Az}\Vert_\infty}{\Vert{z}\Vert_\infty}=\mu \]
- 于是
\[ L=\max\dfrac{\Vert{Ax}\Vert_\infty}{\Vert{x}\Vert_\infty}\ge\dfrac{\Vert{Az}\Vert_\infty}{\Vert{z}\Vert_\infty}=\mu=R \]
希尔伯特矩阵
\[ H_{ij}=\dfrac{1}{i+j-1} \]
- 希尔伯特矩阵的条件数很大
- 解线性方程组 \(Hx=b\) 就是一个病态问题
定理
- 由定义,有
\[ {\Vert{Ax}\Vert}\le\Vert{A}\Vert\cdot{\Vert{x}\Vert} \]
条件数证明
- 由 \(A(x-x_a)=r\),可以得到 \(x-x_a=A^{-1}r\),于是有
\[ \Vert{x-x_a}\Vert\le\Vert{A^{-1}}\Vert\cdot\Vert{r}\Vert \]
- 因为 \(Ax=b\),于是有
\[ {\Vert{b}\Vert}\le\Vert{A}\Vert\cdot{\Vert{x}\Vert} \]
\[ \Rightarrow\dfrac{1}{\Vert{A}\Vert}\cdot\dfrac{1}{\Vert{x}\Vert}\le\dfrac{1}{\Vert{b}\Vert}\ \]
- 因此有
\[ \dfrac{\Vert{x-x_a}\Vert}{\Vert{x}\Vert}\le\Vert{A^{-1}}\Vert\Vert{A}\Vert\cdot\dfrac{\Vert{r}\Vert}{\Vert{b}\Vert} \]
- 一般情况下可以取到等号,根据证明过程构造即可
3.2 淹没 swamp
- 方程组
\[ \begin{aligned} \left\{ \begin{array}{rcrr} 10^{-20}x_1&+&x_2&=1\\ x_1&+&2x_2&=4 \end{array} \right. \end{aligned} \]
- 当乘子很大的时候,我们发现将第一行式子成大第二行上面的时候,第二行的式子会被淹没(swamp)
- 精度问题导致的
- 因此我们可以通过交换两行顺序的方法,让乘子的绝对值小于 1,避免上述情况发生
- 部分主元方法