计算方法B.裴玉茹.02.非线性方程迭代求解(2)

• 数值分析课本第 1 章（求解方程） + PPT（非线性方程迭代求解）

计算方法B

4. 牛顿法

• 牛顿——拉夫逊方法
• 给定初始估计 \(x_0\)，画出函数 \(f\) 在 \(x_0\) 的切线，用切线来近似函数 \(f\)，求出其与 \(x\) 轴的交点作为 \(f\) 的根

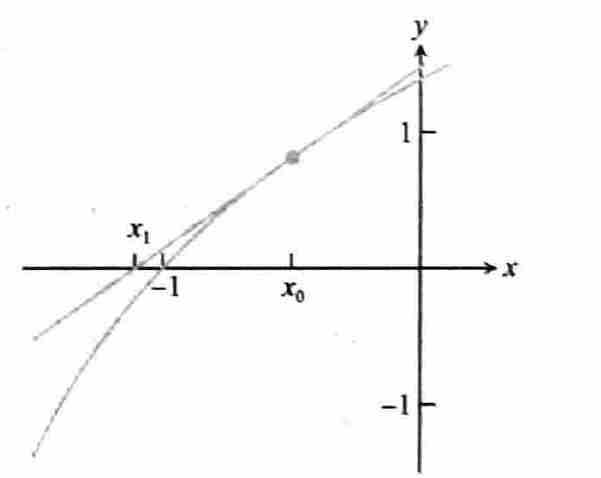
• 算法流程

\[ \begin{aligned} \begin{array}{c} x_0=初始估计\\ x_{i+1}=x_{i}-\dfrac{f(x_i)}{f'(x_i)}\\ \end{array} \end{aligned} \]

• 推导
  • 切线：\(y=f'(x_i)(x-x_i)+f(x_i)\)
  • 令 \(y=0\) 即可

二次收敛

\[ M=\lim_{i\to\infty}\dfrac{e_{i+1}}{e^2_{i}}<\infty \]

• 牛顿方法是二次收敛的
  • 令 \(f\) 是二阶连续可微函数，\(f(r)=0\)，如果 \(f'(r)\ne0\)，则牛顿方法局部收敛到 \(r\)
  • 第 \(i\) 步的误差 \(e_i\) 满足如下式子

\[ \lim_{i\to\infty}\dfrac{e_{i+1}}{e^2_{i}}=M=\dfrac{f''(r)}{2f'(r)} \]

• 证明
  • 局部收敛：FPI 的特殊情况，可以计算得到 \(g'(r)=0<1\)
  • 二次收敛：泰勒展开，要求 \(f'(r)\ne0\)

\[ \begin{aligned} \begin{array}{c} 0=f(r)=f(x_i)+(r-x_i)f'(x_i)+\dfrac{(r-x_i)^2}{2}f''(c)\\ x_{i}-\dfrac{f(x_i)}{f'(x_i)}-r=\dfrac{(r-x_i)^2}{2f'(x_i)}f''(c)\\ e_{i+1}=\dfrac{e_i^2}{2f'(x_i)}f''(c)\\ \dfrac{e_{i+1}}{e^2_{i}}=\dfrac{f''(c)}{2f'(x_i)}\\ c\ 和\ x_i\ 都会收敛到\ r\Rightarrow\lim_{i\to\infty}\dfrac{e_{i+1}}{e^2_{i}}=\dfrac{f''(r)}{2f'(r)}\\ \end{array} \end{aligned} \]

• 误差公式近似为 \(e_{i+1}\approx Me^2_{i}\)

重根

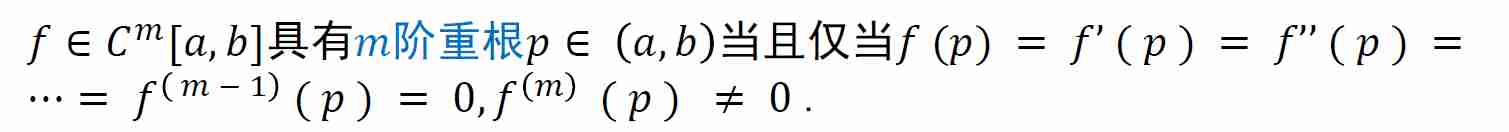
• 如果不满足 \(f'(r)\ne0\)，则收敛速度变为线性
  • 例子：\(f(x)=x^{m}\) 求根
  • 牛顿公式：\(x_{i+1}=x_i-\dfrac{x^{m}_i}{mx^{m-1}_i}=\dfrac{m-1}{m}x_{i}\)

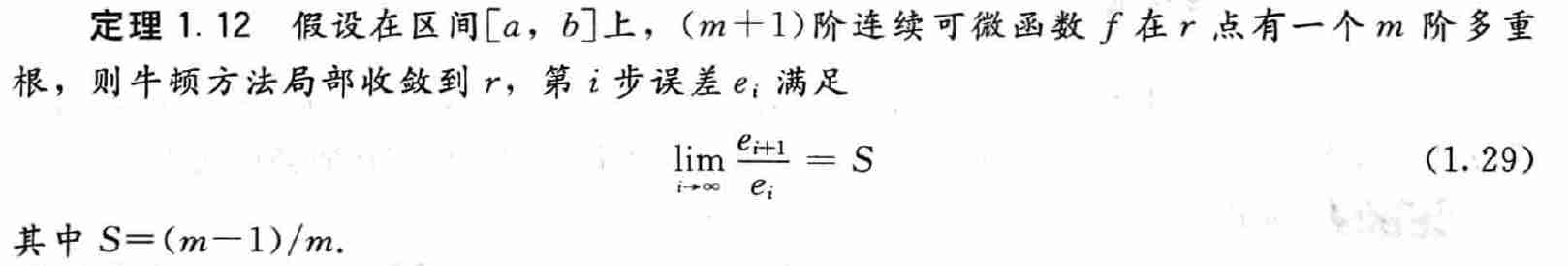
修正方法1

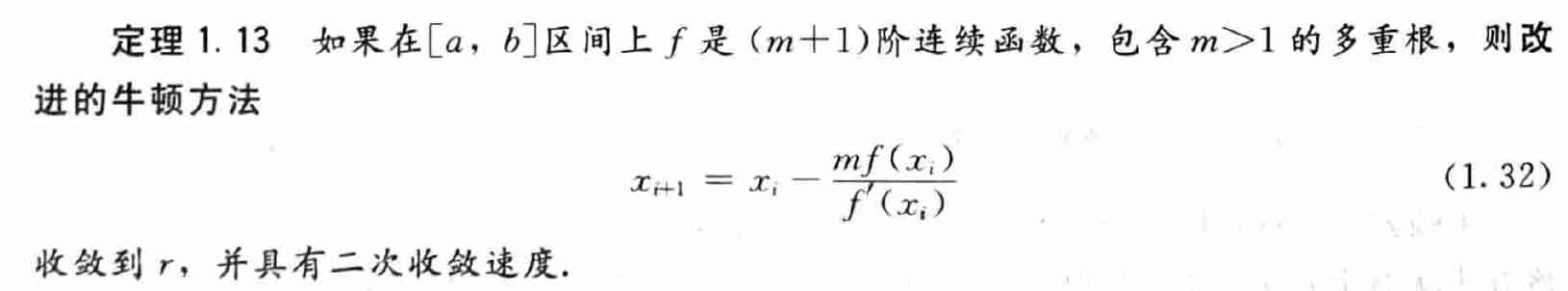
修正方法2

\[ \mu(x)=\dfrac{f(x)}{f'(x)} \]

\[ \begin{aligned} \mu(x)=&\dfrac{(x-p)^mq(x)}{m(x-p)^{m-1}q(x)+(x-p)^mq'(x)}\\ =&{\color{red}(x-p)}\dfrac{q(x)}{mq(x)+(x-p)q'(x)}\\ \end{aligned} \]

• 发现 \(p\) 是 \(\mu\) 的单根

\[ \dfrac{q(p)}{mq(p)+(p-p)q'(x)}=\dfrac{1}{m}\ne0 \]

• 关于 \(\mu\) 应用牛顿方法

\[ g(x)=x-\dfrac{f(x)f'(x)}{[f'(x)]^2-f(x)f''(x)} \]

• 在单根的情况下，修正牛顿方法和原始牛顿方法的收敛速度都快，但是需要更大的计算量

牛顿方法失效

• 例子

\[ f(x)=4x^4-6x^2-\dfrac{11}{4},x_0=\dfrac{1}{2} \]

• 只有在根近邻的初始估计才能收敛到根

5. 不需要导数的根求解

• 导数需要除以一个较小的值，这样可能会引入误差

割线方法

• 使用差商来代替导数

\[ \dfrac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \]

\[ f'(x_{i-1})=\lim_{x_{i}\to{x_{i-1}}}\dfrac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \]

• 算法流程

\[ \begin{aligned} \begin{array}{c} x_0,x_1=初始估计\\ x_{i+1}=x_{i}-\dfrac{f(x_i)(x_i-x_{i-1})}{f(x_i)-f(x_{i-1})}\\ \end{array} \end{aligned} \]

• 误差分析
  • 第一个式子可以通过割线方法的递推式推导得到（右边通分，构造出 3 个误差项）
  • 第二个式子将一般形式 \(e_{i+1}=Ce_{i}^k\) 代入第一个式子解出来即可

• 超线性收敛

割线方法的推广形式

试位方法

• Regula Falsi 方法
• 与二分法相似，但是其中的中点被割线和 \(x\) 轴的交点代替

\[ \begin{aligned} \begin{array}{rl} 割线:&y=\dfrac{f(a)-f(b)}{a-b}(x-a)+f(a)\\ 令\ y=0:&x=\dfrac{bf(a)-af(b)}{f(a)-f(b)} \end{array} \end{aligned} \]

• 算法流程

• 试位方法可能在某些例子中收敛的更慢
• 不保证收敛

Muller 方法

• 通过之前计算的 3 个点（\(x_0,x_1,x_2\)），画出他们的抛物线 \(y=p(x)\)，求出和 \(x\) 轴的交点，作为接下来对 \(x\) 的近似估计
  • 如果有 2 个交点，选择离 \(x_2\) 较近的点
  • 如果有 0 个交点，出现复数解

逆二次插值 IQI

• 和 Muller 方法相同，但是使用的抛物线是 \(x=p(y)\)，保证和 \(x\) 轴只有一个交点

• 拉格朗日插值的一个例子
• 迭代更新的两种方法
  • \(x_i,x_{i-1},x_{i-2}\) 更新为 \(x_{i+1},x_i,x_{i-1}\)
  • \(x_i,x_{i-1},x_{i-2}\) 中去掉后向误差最大的那个，然后加上 \(x_{i+1}\)
• Muller 方法和逆二次插值 IQI 比割线方法收敛更快（更高阶的插值计算）

Brent 方法

• 混合迭代技术
• 兼具：二分法的保证收敛性质、更加复杂方法的快速收敛性质
• Dekker 和 Van Wijingaarden 提出（20 世纪 60 年代）

6. PPT 补充

不动点存在且唯一

• 不是充要条件
• 如果满足如下两个条件，则不动点存在且唯一

• 条件：自身映射、连续、导数小于1
• 证明
  • 存在性：设函数 \(h(x)=g(x)-x=0\)，要么端点成立，要么由介值定理存在一个数使其成立
  • 唯一性：假设存在两个 \(p,q\)，推出矛盾

\[ \vert{p-q}\vert=\vert{g(p)-g(q)}\vert=g'(\xi)\vert{p-q}\vert<\vert{p-q}\vert \]

不动点迭代收敛

• 条件：自身映射、连续、导数小于1
• 证明：中值定理

\[ \begin{aligned} \begin{array}{c} \vert{p_{n}-p}\vert=\vert{g(p_{n-1})-g(p)}\vert=\vert{g'(\xi)}\vert\vert{p_{n-1}-p}\vert\\ \vert{p_{n}-p}\vert\le k\vert{p_{n-1}-p}\vert\le\cdots\le k^{n}\vert{p_0-p}\vert\\ \lim_{n\to\infty}\vert{p_{n}-p}\vert=\lim_{n\to\infty}k^n\vert{p_{0}-p}\vert=0\\ \end{array} \end{aligned} \]

推论

• 如果函数 \(g\) 满足不动点定理, 则利用 \(p_n\) 近似 \(p\) 的误差界如下

\[ \begin{aligned} \begin{array}{c} \vert{p_{n}-p}\vert\le k^{n}\max\{p_0-a,b-p_0\}\\ \vert{p_{n}-p}\vert\le \dfrac{k^{n}}{1-k}\vert{p_1-p_0}\vert\\ \end{array} \end{aligned} \]

• 第一个式子显然
• 第二个式子

\[ \begin{aligned} \begin{array}{c} \vert{p_{n+1}-p_{n}}\vert=\vert{g(p_{n})-g(p_{n-1})}\vert=\vert{g'(\xi)}\vert\vert{p_{n}-p_{n-1}}\vert\le k\vert{p_{n}-p_{n-1}}\vert\\ \vert{p_{n+1}-p_{n}}\vert\le k\vert{p_{n}-p_{n-1}}\vert\le\cdots\le k^{n}\vert{p_1-p_0}\vert\\ \end{array} \end{aligned} \]

\[ \begin{aligned} \begin{array}{rl} \vert{p_{m}-p_{n}}\vert&=\vert{p_{m}-p_{m-1}+p_{m-1}-\cdots-p_{n}}\vert\\ &\le\vert{p_{m}-p_{m-1}}\vert+\vert{p_{m-1}-p_{m-2}}\vert\cdots\vert{p_{n+1}-p_{n}}\vert\\ &=\vert{p_1-p_0}\vert(k^{m-1}+k^{m-2}+\cdots+k^{n})\\ &=\vert{p_1-p_0}\vert k^{n}(k^{m-n-1}+\cdots+1)\\ \end{array} \end{aligned} \]

\[ \begin{aligned} \begin{array}{rl} \vert{p-p_{n}}\vert&=\lim_{m\to\infty}\vert{p_m-p_n}\vert\\ &\le\lim_{m\to\infty}\vert{p_1-p_0}\vert k^{n}(k^{m-n-1}+\cdots+1)\\ &=\vert{p_1-p_0}\vert k^{n}\sum_{i=0}^{\infty}{k^i}\\ &=\dfrac{k^{n}}{1-k}\vert{p_1-p_0}\vert\\ \end{array} \end{aligned} \]

牛顿法

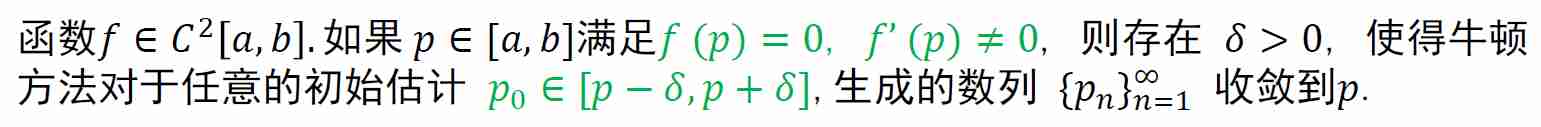
• 证明方法
  • 自身映射，导数小于 1（连续）
• 在满足假设条件的情况下，只要选择足够精确的初始近似，牛顿法就会收敛
• 缺点：需要知道 \(f\) 在每个近似点的导数

迭代方法的误差

• 收敛速度

• 总结

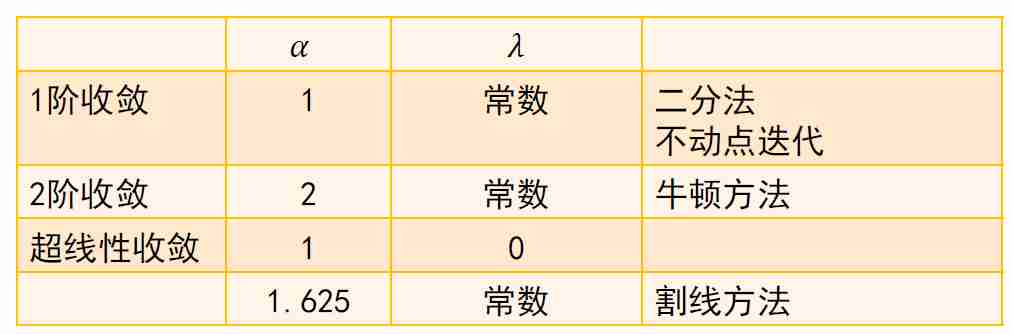
线性收敛

• 自身映射、连续、导数小于1

二阶收敛

• 证明方法就是上面的牛顿方法证明

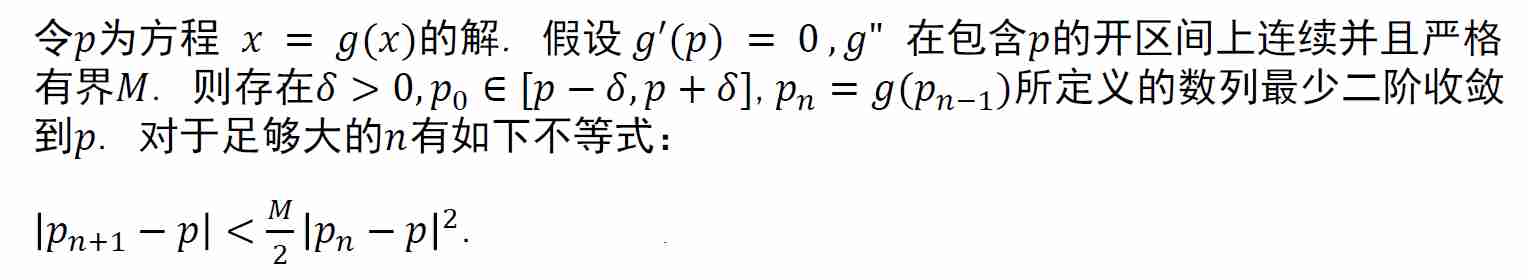
• 在有限的迭代后，二阶收敛所能达到的有效数字的位数远大于线性收敛所能达到的有效数字的位数
• 构造二阶收敛

\[ \begin{aligned} \begin{array}{cr} g(x)=x-\phi(x)f(x)&\\ 0=g'(p)=1-\phi'(p)f(p)-\phi(p)f'(p)=1-\phi(p)f'(p),&f(p)=0\\ \phi(x)=\dfrac{1}{f'(x)}&\\ p_{n+1}=p_{n}-\dfrac{f(p_{n})}{f'(p_{n})} \end{array} \end{aligned} \]

高阶收敛

• 形式上看和泰勒展开一致

加速收敛

• \(\mathrm{Aitken's}\ \Delta^2\)方法
• 加速任何线性收敛的序列
  • 引入了更多的计算达到超线性收敛
  • 每次根据之前的 3 个估计进行加速

• \(n\) 足够大的时候

\[ \dfrac{p_{n+1}-p}{p_n-p}\approx\dfrac{p_{n+2}-p}{p_{n+1}-p} \]

\[ p\approx \dfrac{p_{n}p_{n+2}-p_{n+1}^2}{p_n-2p_{n+1}+p_{n+2}}=p_n-\dfrac{(p_{n+1}-p_{n})^2}{p_n-2p_{n+1}+p_{n+2}} \]

\[ \hat{p}=p_n-\dfrac{(p_{n+1}-p_{n})^2}{p_n-2p_{n+1}+p_{n+2}} \]

• 考虑前向差分公式

\[ \begin{aligned} \begin{array}{c} \Delta{p_i}=p_{i+1}-p_{i}\\ \Delta^k{p_i}=\Delta^{k-1}(\Delta{p_i})=\Delta^{k-1}{p_{i+1}}-\Delta^{k-1}{p_{i}}\\ \hat{p}=p_n-\dfrac{(\Delta{p_{n}})^2}{\Delta^2{p_{n}}} \end{array} \end{aligned} \]

• 每 3 个估计值更新一次
  • 超线性收敛

• 更新之后的值马上用来计算
  • 二阶收敛