计算方法B.裴玉茹.02.非线性方程迭代求解

Posted on Edited on In Views:
非线性方程迭代求解、二分法、不动点迭代、精度的极限
  • 数值分析课本第 1 章（求解方程） + PPT（非线性方程迭代求解）

非线性方程迭代求解

  • 求解方程

1. 二分法

  • 原理

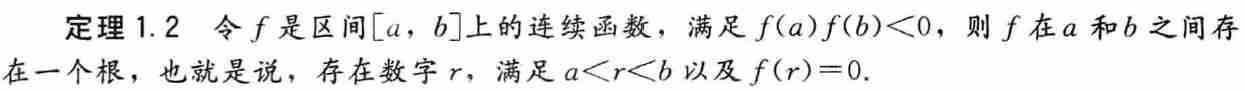
  • 算法流程

速度与准确性

  • 初始区间 \([a,b]\)
  • 最终选择区间的中点作为近似解
  • \(n\) 步二分法之后
    • 求解误差 \(=\vert{x_c-r}\vert\le\dfrac{b-a}{2^{n+1}}\)
      • 绝对误差界
    • 函数计算次数：\(n+2\)
  • 和有效数字类似的定义
    • 定义：如果误差小于 \(0.5\times10^{-p}\)，阶精确到小数点后 \(p\) 位

终止条件

  • 绝对误差小于容差
  • 相对误差小于容差
  • 后向误差小于容差

实际计算的问题

避免向上溢出

  • 使用 \(p_{n}=a_n+\dfrac{b_n-a_n}{2}\) 来代替 \(p_n=\dfrac{b_n+a_n}{2}\)

避免乘法运算

  • 使用符号函数 \(\mathrm{sgn}\)
  • 使用 \(\mathrm{sgn}(f(a_n))\cdot\mathrm{sgn}(f(p_n))<0\) 代替 \(f(a_n)\cdot f(b_n)<0\)

2. 不动点迭代

  • FPI：Fixed Point Iteration
  • 定义：当 \(g(r)=r\)，实数 \(r\) 是函数 \(g\) 的不动点
  • \(g(x)\) 的不动点，同时也是 \(x=f(x)\) 的解
  • 不动点迭代：\(g(x)\)
    • \(x_0\) = 初始估计
    • \(x_{i+1}=g(x_i)\)
  • 无穷多步迭代之后，序列 \(\{x_i\}\) 可能收敛，也可能发散
  • 如果函数 \(g\) 连续，而且 \(\{x_i\}\) 收敛到 \(r\)，则 \(r\) 是函数 \(g\) 对应的不动点

\[ g(r)=g(\lim_{i\to\infty}{x_i})=\lim_{i\to\infty}g(x_i)=\lim_{i\to\infty}x_{i+1}=r \]

多种形式

  • \(x^3+x-1=0\)
  • 可以使用如下的不动点迭代方式
    • \(x=1-x^3=g_1(x)\)
    • \(x=\sqrt[3]{1-x}=g_2(x)\)
    • \(x=\dfrac{1+2x^3}{1+3x^2}=g_3(x)\)
  • 一些现象
    • 起始点为 \(x_0=0.5\) 时，\(g_1(x)\) 未收敛，在 \(0,1\) 两个数上跳跃
    • 起始点为 \(x_0=0.5\) 时，\(g_2(x)\) 收敛了
    • 起始点为 \(x_0=0.5\) 时，\(g_3(x)\) 收敛了，比 \(g_2(x)\) 更快
  • cobweb 图

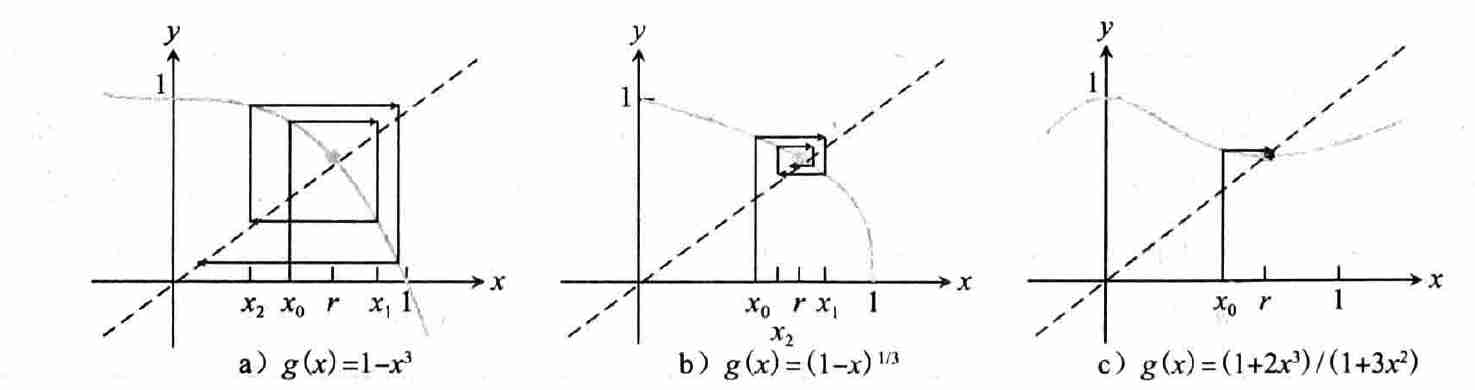
线性收敛

  • 定义：令 \(e_i\) 表示迭代过程中第 \(i\) 步时的误差，如果有如下式子成立，该方法被称为满足线性收敛，收敛速度为 \(S\)

\[ \lim_{i\to\infty}\dfrac{e_{i+1}}{e_{i}}=S \]

局部收敛

  • 定理
    • 可导函数的导函数不存在第一类间断点，只可能存在第二类间断点

  • 定义：如果一个迭代方法对于一个足够接近 \(r\) 的初值能收敛到 \(r\)，该迭代方法被称为局部收敛到 \(r\)
    • 如果存在近邻区间 \((r-\epsilon,r+\epsilon)\)，其中 \(\epsilon>0\)，使得近邻区间种的所有初始估计都可以收敛到 \(r\)，那么该方法局部收敛到 \(r\)
    • 定理 1.6 的结论：当 \(\vert{g'(r)}\vert<1\) 时不动点迭代局部收敛
  • FPI 计算 \(\sqrt{2}\)

\[ f(x)=\dfrac{x+\dfrac{2}{x}}{2} \]

终止条件

  • 无法通过初始值和迭代次数，预测达到给定容差所需要进行的步数
  • 绝对误差：\(\vert{x_{i+1}-x_{i}}\vert<TOL\)
  • 相对误差（要求解不在 0 附近）：\(\dfrac{\vert{x_{i+1}-x_{i}}\vert}{\vert{x_{i+1}}\vert}<TOL\)
  • 混合绝对/相对误差（可用于解在 0 附近）：\(\dfrac{\vert{x_{i+1}-x_{i}}\vert}{\max{(\vert{x_{i+1}}\vert},\theta)}\)
  • 同时设置最大迭代步数，防止收敛失败

和二分法的对比

  • 区别
    • 二分法保证线性收敛
    • 不动点迭代仅仅是局部收敛。当不动点迭代收敛时，其线性收敛
  • 相同
    • 迭代的每一步都只需要进行一次函数求值

3. 精度的极限

  • 计算机的精度是有限的
  • 二分法可能在中间的某一步停止，此时函数值可能不为 0，但是由于精度问题，计算计算出来的值未 0
    • 这不是二分法的问题，而是计算机本身精度不够导致的

前向误差与后向误差

  • 假设 \(f\) 是一个函数，\(r\) 是一个根，即 \(f(r)=0\)。假设 \(x_a\) 时 \(r\) 的近似值。对于根求解问题，近似 \(x_a\) 的后向误差是 \(\vert{f(x_a)}\vert\)，前向误差是 \(\vert{r-x_a}\vert\)
  • 前向后向的解释

  • 重根

  • 在多根附近，函数变化十分缓慢，垂直方向的后向误差通常比水平方向的前向误差小得多

终止条件

  • 如何设定方程求解器的终止条件？
    • \(\vert{x_a-r}\vert\) 足够小（前向误差）
    • \(\vert{f(x_a)}\vert\) 足够小（后向误差）
  • 二分法两种误差都可观测
    • 前向误差：可控，不会大于当前区间的一半
    • 后向误差：可计算
  • FPI：只能计算出后向误差
  • 其他的终止条件：计算时间

威尔金森多项式

  • 数值求解很难的单根例子

\[ W(x)=(x-1)(x-2)\cdots(x-20) \]

  • 展开后的形式很长 \(\dots\dots\)
    • 对展开的形式求根困难
    • 求根过程中保存系数的很小误差会被放大，对结果产生很大影响

根搜索的敏感性

  • 方程中小的求解误差造成求解根中的大误差
  • 敏感性问题
    • 在输入中是一个小误差，在这种情况下我们对问题进行求解，造成输出中的大问题
  • 通过误差放大因子和条件数定量描述
  • 假定 \(f(x)=0\) 的根为 \(x=r\)，我们对输入做了一个小变化 \(\epsilon g(x)\)（\(\epsilon\) 可能很小），令 \(\Delta r\)是对应根中的变化

\[ f(r+\Delta r)+\epsilon g(r+\Delta r)=0 \]

  • 一阶泰勒展开

\[ f(r)+(\Delta r)f'(r)+\epsilon g(r)+\epsilon(\Delta r)g'(r)+O((\Delta r)^2) \]

  • 忽略高阶项

\[ (\Delta r)(\epsilon g'(r)+f'(r))\approx-f(r)-\epsilon g(r)=-\epsilon g(r) \]

  • 假定 \(\epsilon\) 相对于 \(f'(r)\) 来说很小，而且 \(f'(r)\ne0\)

\[ \Delta r=\dfrac{-\epsilon g(r)}{\epsilon g'(r)+f'(r)}\approx\dfrac{-\epsilon g(r)}{f'(r)} \]

根的敏感性公式

  • 假定 \(r\) 是 \(f(r)\) 的根，并且 \(r+\Delta r\) 是 \(f(x)+\epsilon g(x)\) 的根，则当 \(\epsilon<<f'(r)\) 时

\[ \Delta r\approx\dfrac{-\epsilon g(r)}{f'(r)} \]

误差放大因子

  • 相对前向误差 / 相对后向误差
  • 求根过程中的误差放大因子

\[ \left\vert\dfrac{\dfrac{\Delta r}{r}}{\dfrac{\epsilon g(r)}{g(r)}}\right\vert\approx\left\vert{\dfrac{\dfrac{-\epsilon g(r)}{rf'(r)}}{\epsilon}}\right\vert=\left\vert{\dfrac{g(r)}{rf'(r)}}\right\vert \]

条件数

  • 条件数：与算法无关，与问题本身有关
  • 稳定：与算法相关，而不是问题本身