计算方法B.裴玉茹.01.基础知识

Posted on 2021-09-25 Edited on 2021-11-20 In computation.pyr Views:

基础知识、多项式求值（嵌套乘法）、实数的浮点表示、误差、有效数字缺失、微积分回顾

数值分析课本第 0 章（基础知识） + PPT（误差）

基础知识

1. 多项式求值

\(x=\dfrac{1}{2},P(x)=2x^4+3x^3-3x^2+5x-1\)
直接求值
- 乘法：10
- 加法：4
计算 \((\dfrac{1}{2})^4\) 保留中间结果
- 乘法：7（\(x^3,x^2\) 不需要重复计算）
- 加法：4
嵌套乘法（霍纳方法）
- 乘法：4
- 加法：4

\[ \begin{aligned} P(x)&=2x^4+3x^3-3x^2+5x-1\\ &=-1+5x-3x^2+3x^3+2x^4\\ &=-1+x(5+x(-3+x(3+x(2))) \end{aligned} \]

嵌套乘法能够通过 d 次乘法和 d 次加法计算 d 阶多项式的值
科学计算方法的所有主题的特征
- 做简单计算的时候速度要快
- 由于简单计算可能会被进行多次，尽可能有效地进行简单计算非常重要
- 最好的计算方法可能不是显而易见的那种方法
多项式的标准形式

\[ \begin{aligned} &c_1+c_2x+c_3x^2+c_4x^3+c_5x^4\\ =&c_1+x(c_2+x(c_3+x(c_4+x(c_5))))\\ \end{aligned} \]

更加一般的形式
- 称 \(r_1,\cdots,r_4\) 为基点

\[ \begin{aligned} &c_1+c_2x+c_3x^2+c_4x^3+c_5x^4\\ =&c_1+(x-r_1)(c_2+(x-r_2)(c_3+(x-r_3)(c_4+(x-r_4)(c_5))))\\ \end{aligned} \]

2. 二进制数字

进制转换
- 整数部分
- 小数部分
2 进制转 10 进制无限循环小数示例

\[ \begin{aligned} x&=(0.\overline{1011})_2\Rightarrow2^4x=(1011.\overline{1011})_2\\ x&=\dfrac{(1011)_2}{2^4-1}=\dfrac{11}{15} \end{aligned} \]

3. 实数的浮点表示

IEEE 标准

精度	符号 S	尾数 M	指数 E
单精度 32	1	8	23
双精度 64	1	11	52
长双精度 80	1	15	64

数的分类
- 规格化数：\(1.M\times2^{E-\mathrm{Bias}}\)
  - 指数不是全 0 或者全 1
  - \(\mathrm{Bias}=2^{k-1}-1\)
    - \(\mathrm{Bias}\) 称为指数偏差
- 非规格化数：\(0.M\times2^{1-Bias}\)
  - 指数全 0
- 无穷大：指数全 1，尾数全 0
- NaN：指数全 1，但是尾数不全为 0

规格化数

以 64 位双精度 为例
机器精度
- 1 和比 1 大的最小浮点数的距离
- \(\epsilon_{\mathrm{mach}}=2^{-52}\)
舍入方式
- 截断
- 四舍五入
- IEEE 舍入最近法则
  - 规则
    - 53 位为 1，进位
    - 53 位为 0，舍去
    - 特殊情况：53 位之后全为 0
      - 52 为 1 则进位，52 位为 0 则舍去
  - 记作 \(\mathrm{fl}(x)\)
舍入误差：\(\vert\mathrm{fl}(x)-x\vert\)
令 \(x_c\) 是计算版本 \(x\) 的精确度量
- 绝对误差：\(\vert x_c-x\vert\)
- 相对误差：\(\dfrac{\vert x_c-x\vert}{x}\)
  - 要求 \(x\) 的度量存在，即 \(x\ne0\)
相对舍入误差

\[ \dfrac{\vert\mathrm{fl}(x)-x\vert}{x}\le\dfrac{1}{2}\epsilon_{\mathrm{mach}} \]

理解如下结果

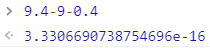
4. 有效数字缺失

近似相等的两个数相减造成有效数字的位数减少
123.4567 - 123.4566 = 0.0001
- 有效位数：(7) - (7) = (1)
3 位小数的计算机上计算 \(\sqrt{9.01}-3\)
- 3 位小数：中间计算的浮点数最多只能有 3 位尾数，有效数字位数肯定也小于 3
- \(\sqrt{9.01}\approx 3.0016662\approx3\)
- 结果为 0
共轭等式

\[ \begin{aligned} \sqrt{9.01}-3&=\dfrac{(\sqrt{9.01}-3)(\sqrt{9.01}+3)}{\sqrt{9.01}+3}\\ &\\ &=\dfrac{9.01-9}{\sqrt{9.01}+3}\\ &\\ &\approx\dfrac{0.01}{3+3}\\ &\\ &=\dfrac{0.01}{3+3}\\ &\\ &\approx1.67\times10^{-3} \end{aligned} \]

三角函数

共轭方法

\[ \dfrac{1-\cos{x}}{\sin^2{x}}=\dfrac{(1-\cos{x})(1+\cos{x})}{\sin^2{x}(1+\cos{x})}=\dfrac{1}{1+\cos{x}} \]

测试

function test(x) {
    console.log((1-Math.cos(x))/(Math.sin(x)*Math.sin(x)));
    console.log(1/(1+Math.cos(x)));
}
// test(1e-2)
// 0.5000125002084805
// 0.5000125002083363

// test(1e-5)
// 0.5000000413868522
// 0.5000000000125

// test(1e-10)
// 0
// 0.5

求解一元二次不等式

求根公式如下，当 \(b^2-4ac\approx0\) 时，某一个根分子出现 \(-b+b\) 的情况

\[ \begin{aligned} x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a} \end{aligned} \]

\(x^2+9^{12}x-3=0\)
- js 测试的结果

\[ x_1=\dfrac{-9^{12}-\sqrt{9^{24}-12}}{2}=-2.824\times10^{11} \]

\[ x_2=\dfrac{-9^{12}+\sqrt{9^{24}-12}}{2}=0 \]

如何减小这种误差：共轭方式

\[ \begin{aligned} x_2&=\dfrac{-b+\sqrt{b^2-4ac}}{2a}\\ &\\ &=-\dfrac{(b-\sqrt{b^2-4ac})(b+\sqrt{b^2-4ac})}{2a(b+\sqrt{b^2-4ac})}\\ &\\ &=-\dfrac{4ac}{2a(b+\sqrt{b^2-4ac})}\\ &\\ &=-\dfrac{2c}{(b+\sqrt{b^2-4ac})} \end{aligned} \]

看具体的 b 的正负性选择正确的表达式
或者利用韦达定理

\[ x_1x_2=\dfrac{c}{a} \]

5. 微积分

中值定理 / 介值定理

连续极限

均值定理 / 中值定理

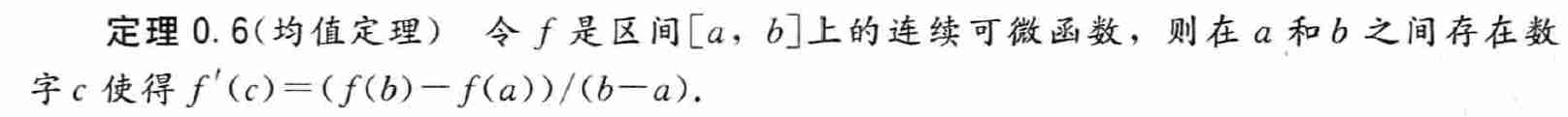
罗尔定理

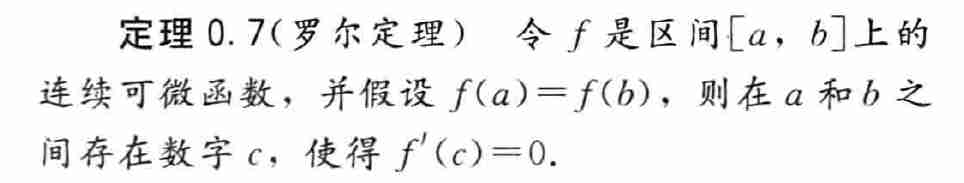
泰勒展开
- 用有限项求和来近似无穷级数
- 以 \(x_0\) 为中心的函数 \(f\) 的 \(k\) 阶泰勒多项式 + 泰勒余项
  - n 阶多项式近似
  - 截断误差
- \(f(x)=P_k(x)+R_k(x)\)

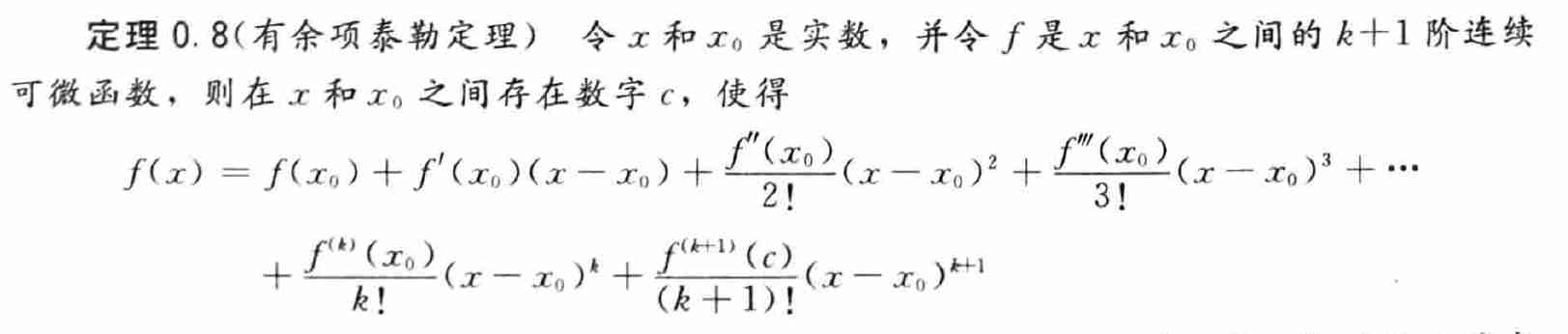
均值定理的积分版本

推广罗尔定理

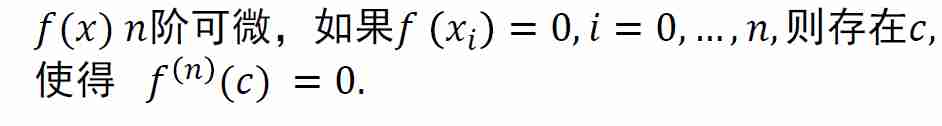
黎曼积分

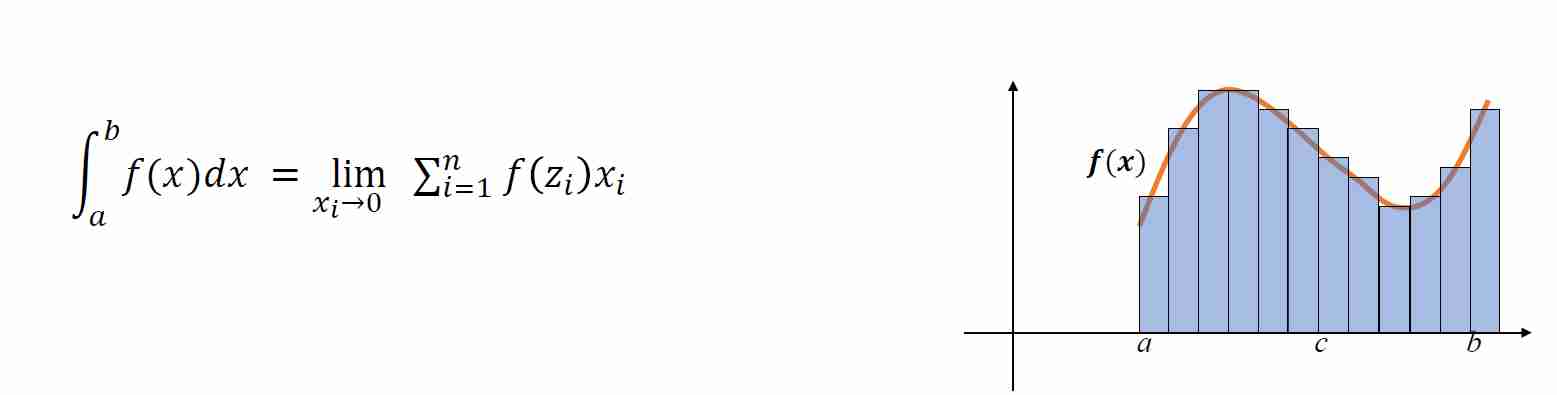
极值定理

6. 误差(10进制)

舍入与截断

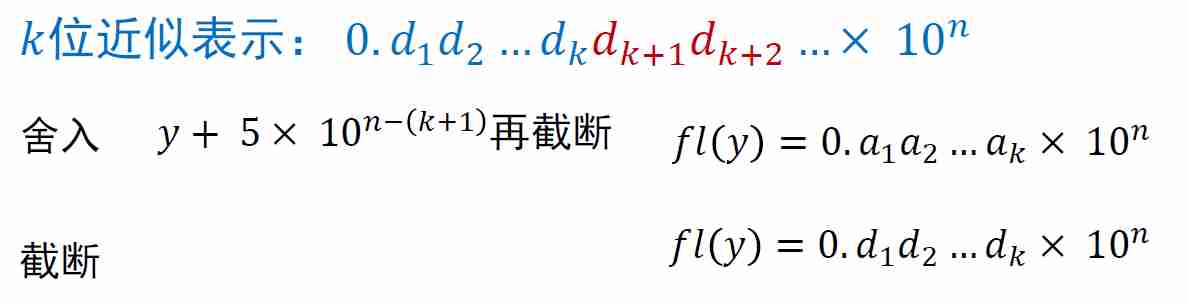
\(p^{\ast}\) 是 \(p\) 的一个近似，\(p=p^{\ast}\pm\epsilon^{\ast}\)
- 绝对误差：\(\vert p-p^{\ast}\vert\)
- 相对误差：\(\dfrac{\vert p-p^{\ast}\vert}{\vert p\vert}\)
- 误差范围：\(\vert e^{\ast}\vert\le\epsilon^{\ast}\)
- 有效数字：\(t\) 为最大非负整数满足 \(\dfrac{\vert p-p^{\ast}\vert}{\vert p\vert}<5\times10^{-t}\)
  - 由于舍入引入的相对误差与有效数字的关系
截断并不能保证 \(k\) 位有效数字

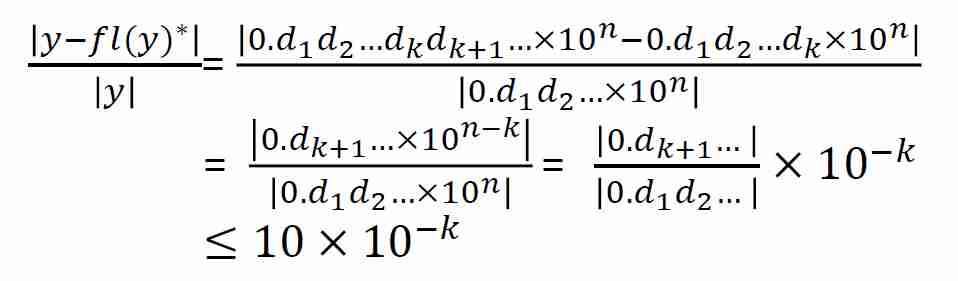
但是实际上，截断引入的相对误差可能比舍入引入的相对误差小
- 上面都是小于号，一个范围估计

产生误差的运算

相近数字相减
除以一个小数值的数

减小误差的方式

避免相近数字相减

\[ \sqrt{x+\epsilon}-\sqrt{x}=\dfrac{\epsilon}{\sqrt{x+\epsilon}+\sqrt{x}} \]

\[ \ln(x+\epsilon)-\ln(x)=\ln(1-\dfrac{\epsilon}{x}) \]

\[ 1-\cos{x}=2\sin^2{\dfrac{x}{2}}\quad(x\to0) \]

\[ e^x-1=x(1+\dfrac{1}{2}x+\dfrac{1}{6}x^2+\cdots)\quad(x\to0) \]

最小化计算的次数（嵌套乘法）
- 随着计算量的减少，累计误差降低

舍入误差

\(p^{\ast}=\pm0.a_1a_2\cdots a_n\times10^m\)
有效数字：\(t\) 为最大非负整数满足

\[ \dfrac{\vert p-p^{\ast}\vert}{\vert p\vert}<5\times10^{-t} \]

\(\vert p-p^{\ast}\vert\le0.5\times10^{m-t}\)（比上面更强）

\[ \begin{align} \begin{array}{**llr**} \vert p-p^{\ast}\vert&\le5\times10^{-n-1}\times10^{m}&\\ &\le0.5\times10^{m-t}&(t\le n)\\ \end{array} \end{align} \]

\(\epsilon_r^{\ast}\le\dfrac{1}{2a_1}\times10^{1-t}\)

\[ \begin{align} 条件:&\\ &(1)\quad\vert p-p^{\ast}\vert\le0.5\times10^{m-t}\\ &(2)\quad\vert p\vert\ge0.a_1\\ 结论:&\\ & \epsilon_r^{\ast}=\dfrac{\vert p-p^{\ast}\vert}{\vert p\vert}\le\dfrac{0.5\times10^{m-t}}{0.a_1\times10^{m}}=\dfrac{1}{2a_1}\times10^{1-t} \end{align} \]

可能用上面的不同式子计算得到的有效数字位数不一样

7. 算法与收敛性

算法的标准——稳定

稳定
- 初始数据中的微小变化会在最终结果中产生相应的小变化
条件稳定
- 仅对特定初值稳定
稳定性是算法的性质
- 稳定指的是针对算法引起的初始误差的放大，而不是问题本身
- 如果一个算法总是能以较小的后向误差提供近似解，则称为稳定算法

问题的条件

问题本身可能是有问题的，无论我们使用怎样的算法都没有用
由于理论问题本身固有的特性造成对初始误差的放大，与用于求解的特定算法无关
例子：蝴蝶效应、混沌现象、气象（洛仑兹方程）

算法的稳定性

指数增长的误差——不稳定
线性增长的误差——稳定

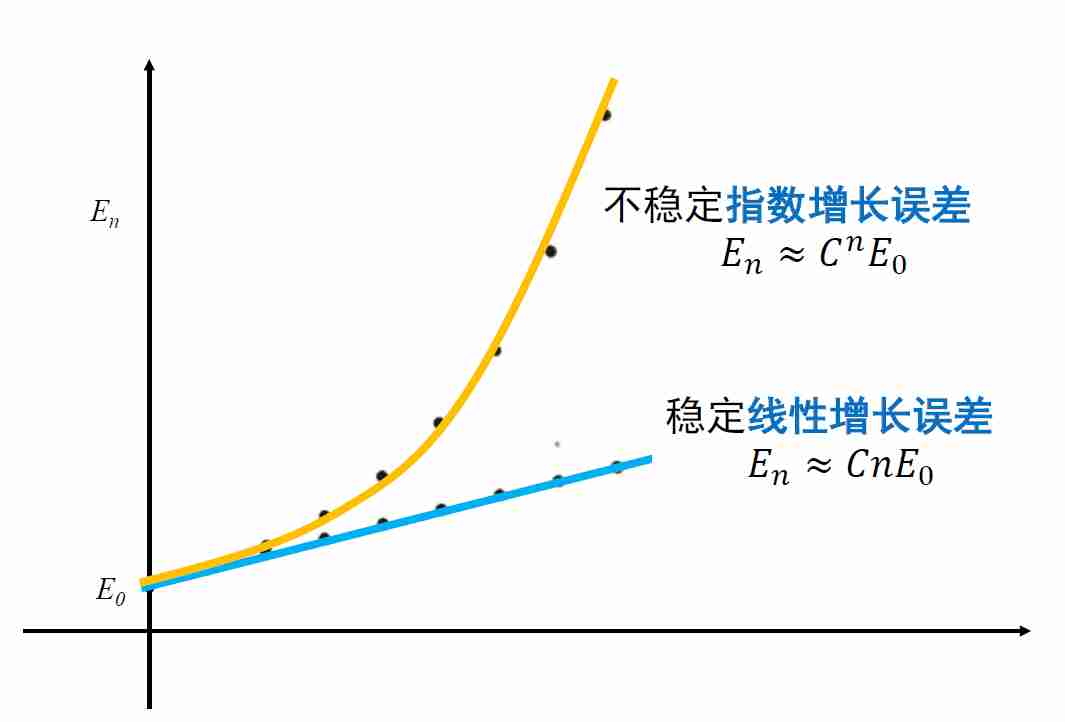
例子

求解

\[ I_n=\dfrac{1}{e}\int_{0}^{1}x^ne^x\;\mathrm{d}x,\quad n=0,1,2,\cdots \]

迭代公式 1（不稳定）

\[ I_n=1-nI_{n-1} \]

分部积分得到，首先计算 \(I_0\)，之后迭代计算
误差推导

\[ \vert{E_0}\vert=\vert{I_0-I_0^{\ast}}\vert \]

\[ \vert{E_n}\vert=\vert{I_n-I_n^{\ast}}\vert=\vert{(1-nI_{n-1})-(1-nI_{n-1}^{\ast})}\vert=n\vert{E_{n-1}}\vert=\cdots=n!\vert{E_{0}}\vert \]

迭代公式 2（稳定）

\[ I_n=1-nI_{n-1}\Rightarrow I_{n-1}=\dfrac{1-I_{n}}{n} \]

首先计算得到 \(I_N^{\ast}\)

\[ I_N\ge\dfrac{1}{e}\int_{0}^{1}x^Ne^0\;\mathrm{d}x=\dfrac{1}{e(N+1)} \]

\[ I_N\le\dfrac{1}{e}\int_{0}^{1}x^Ne^1\;\mathrm{d}x=\dfrac{1}{N+1} \]

\[ I_N^{\ast}=\dfrac{1}{2}(\dfrac{1}{e(N+1)}+\dfrac{1}{N+1}) \]

误差推导

\[ \vert{E_n}\vert=\dfrac{\vert{E_{n+1}}\vert}{n+1}=\cdots=\dfrac{\vert{E_{N}}\vert}{(n+1)\cdots{(N-1)}{N}} \]

收敛速度

数列

函数