GAMES102.刘利刚.02.参数曲线拟合
- https://www.bilibili.com/video/BV1NA411E7Yr
参数曲线拟合
一元函数
- \(y=f(x)\)
- \(f:R^1\to R^1\)
- 数据拟合的方法
- 三步曲:到哪找、 找哪个、怎么找
- 到哪找
- 确定某个函数集合(“池子”),具有某种结构容易表达(比如线性函数空间),且尽量广泛(表达能力强)
- 找哪个
- 度量哪个函数是好的/ “最好” 的,定义损失函数,包括数据误差项(逼近数据的度量)与正则项(对函数性质的度量)
- 怎么找
- 优化求解:不同的优化方法与技巧
- 线性问题:解线性方程或线性方程组
- 非线性问题:
- 凸问题:有理论保证
- 非凸问题:难!数值求解( 梯度下降法、牛顿法、拟牛顿法、L‐BFGS,
···),须选择合适初值、步长等;一般要根据具体的优化问题形式及特点来设计合适的优化方法!
- 很难找到全局的最值
- 蚁群算法、遗传算法、模拟退火算法、···
- 优化求解:不同的优化方法与技巧
多元函数
多个变量的函数
\(y=f(x_1,x_2,\cdots,x_n)\)
- \(f:R^n\to R^1\)
\[ \begin{pmatrix} x_1\\ \cdots\\ x_n\\ \end{pmatrix} \to y \]
- 一个二元函数的例子
- \(z=f(x,y),(x,y)\in[0,1]\times[0,1]\)
- 升维可视化:\(\Big(x,y,f(z,y)\Big)\)
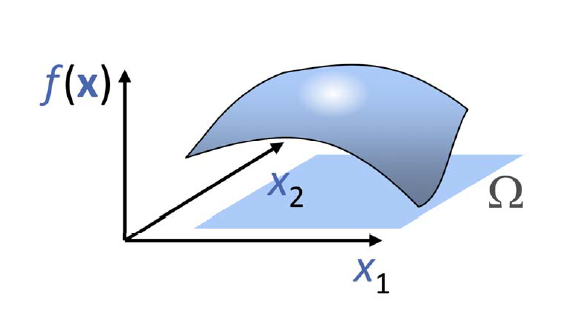
- 三元函数可视化则变得困难
- 升维则是四维
- 高维函数不容易直观看到结果
二元/多元函数的基函数构造
张量积
- 张量积形式
- 即用两个一元函数的基函数的相互乘积来定义
- 例如:二次二元多项式函数 \(z=f(x,y)\) 的基函数 \(\{1,x,y,x^2,xy,y^2\}\)
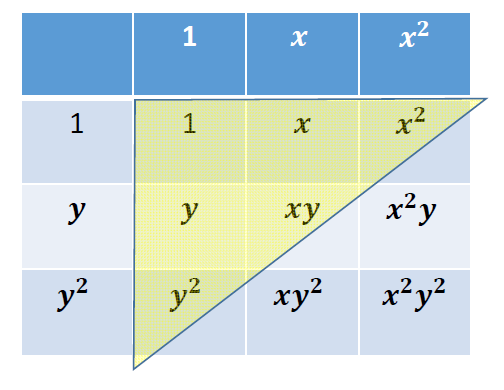
- 拟合的方法和之前相似,就是拟合上面各个项的系数
- 也可以使用其他的基函数,不一定是多项式基函数
- 三次二元多项式函数
- 取次数不超过 \(3\) 的,和上面一样画三角形

- 两个方向的基函数也可以不同
- 但是这样处理起来比较麻烦
- 使用相同的基函数称为共享基函数,方便计算处理
张量积评价
- 优点
- 定义简单,多个一元基函数的乘积形式
- 不足
- 随着维数增加,基函数个数急剧增加,导致变量急剧增加
- (求解系统规模急剧增加,求解代价大)
- \(O(\dfrac{n^2}{2})\)
多元函数的神经网络表达
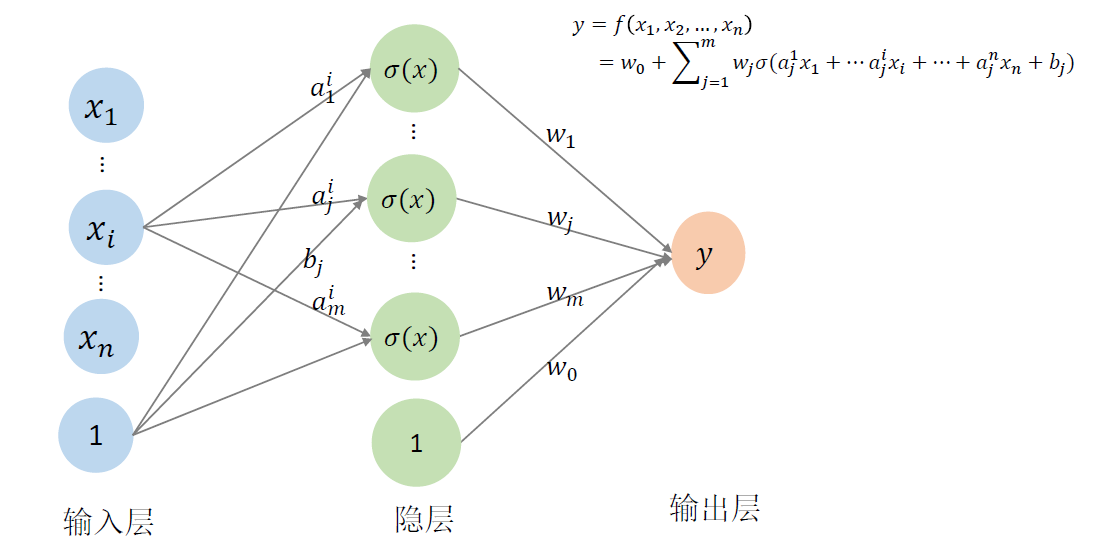
- 用一个单变量函数 \(\sigma(x)\) (称为激活函数)的不同仿射变换来构造 “基函数”:基函数数目可控
- 维数由中间结点数目的个数决定
- 梯度下降 + 链式法则
- 反向传播算法
- 存在的问题
- 中间结点个数选择:过拟合 / 欠拟合
- 多层网络结构
- 多隐层
- 把 n 维空间的一个点转化到 m 维空间的一个点(还可以进行变换),这样可能可以让这些点的分布散开
- 神经网络的本质就是进行函数拟合
- 卷积、池化
- 一些特殊的操作
- 共用参数、降维
向量值函数
- 多个应变量
单变量
- \(f:R^1\to R^m\)
\[ x\to \begin{pmatrix} y_1\\ \cdots\\ y_m\\ \end{pmatrix} \]
- 看成多个单变量函数,各个函数独立无关
- 在某些情况下,可能要求函数之间有一些相关性
- 一般会用同样的基函数(共享基函数)
- 结构一样,但是系数是不一样的
\[ \left\{ \begin{array}{lr} y_1=f_1(x)\\ \cdots\\ y_m=f_m(x)\\ \end{array} \right. \]
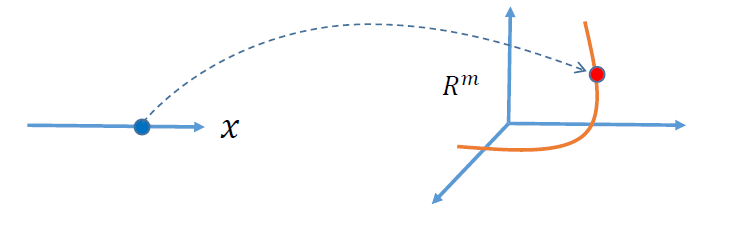
- 几何解释
- 一个实数 \(x\in R^1\) 映射到 m 维空间 \(R^m\) 的一个点,轨迹构成 \(R^m\) 的一条 “曲线”
- 本质维度(本征维度)为 1
- 嵌入空间是 \(m\) 维的
- 曲线的本质维度为 1
特例:平面参数曲线
- \(f:R^1\to R^2\)
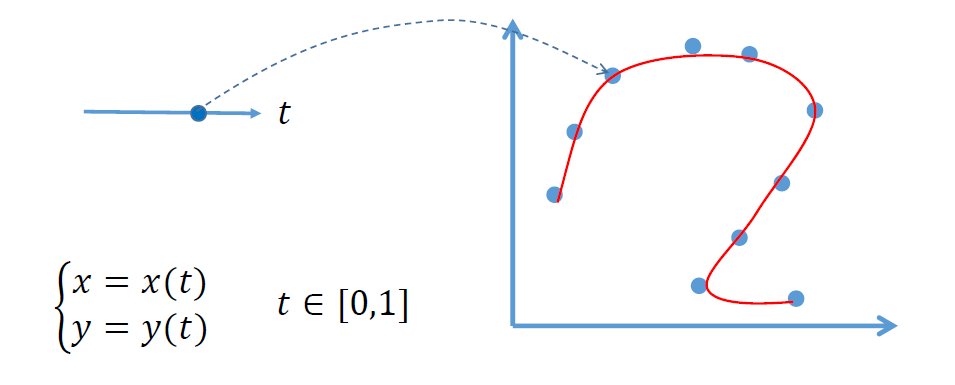
\[ \left\{ \begin{array}{**lr**} x=x(t)\\ y=y(t)\\ \end{array} \right. t\in[0,1] \]
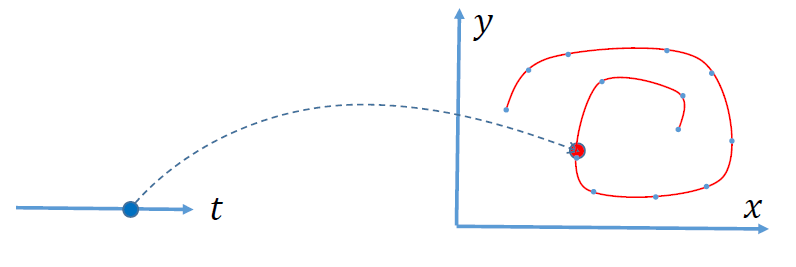
- 几何解释:
- 一条曲线由一个变量参数 \(t\) 决定,也称为单参数曲线
- 参数 \(t\) 可看成该曲线的 “时间” 变量
- 可灵活表达非函数型的曲线(任意曲线)
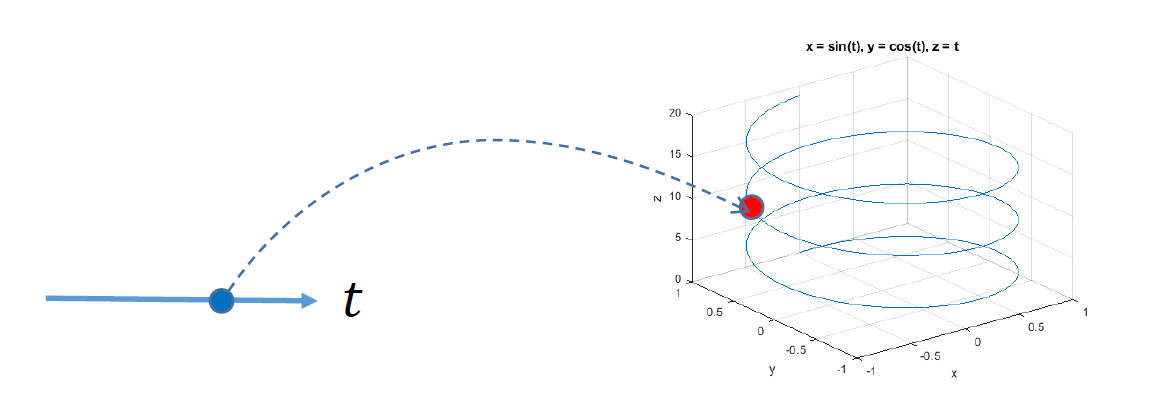
特例:空间参数曲线
- \(f:R^1\to R^3\)
\[ \left\{ \begin{array}{**lr**} x=x(t)\\ y=y(t)\\ z=z(t)\\ \end{array} \right. t\in[0,1] \]
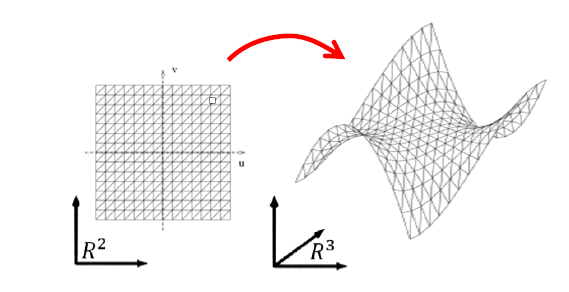
特例:参数曲面
- \(f:R^2\to R^3\)
\[ \left\{ \begin{array}{**lr**} x=x(u,v)\\ y=y(u,v)\\ z=z(u,v)\\ \end{array} \right. (u,v)\in[0,1]\times[0,1] \]
- 几何解释
- 一张曲面由两个参数 u,v 决定,也称为双参数曲面
- 可灵活表达非函数型的任意曲面
- 流形
- 只是位于三维空间中的一层,称为流形
- 虽然处在三维空间中,本质上是二维的
- 流形:任何一个点,其周围无穷小的区域等价于平面的一个圆盘
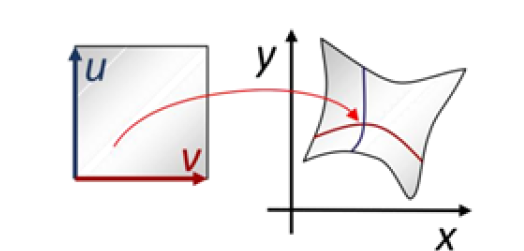
特例:二维映射
- \(f:R^2\to R^2\)
\[ \left\{ \begin{array}{**lr**} x=x(u,v)\\ y=y(u,v)\\ \end{array} \right. (u,v)\in[0,1]\times[0,1] \]
- 几何解释
- 二维区域之间的映射
- 可看成特殊的曲面(第三个维度始终为0)
- 应用:图像变形
特例:三维映射
- \(f:R^3\to R^3\)
\[ \left\{ \begin{array}{**lr**} x=x(u,v,w)\\ y=y(u,v,w)\\ z=z(u,v,w)\\ \end{array} \right. (u,v,w)\in[0,1]^3 \]
- 几何解释:
- 三维体区域之间的映射
- 应用:体形变、体参数化
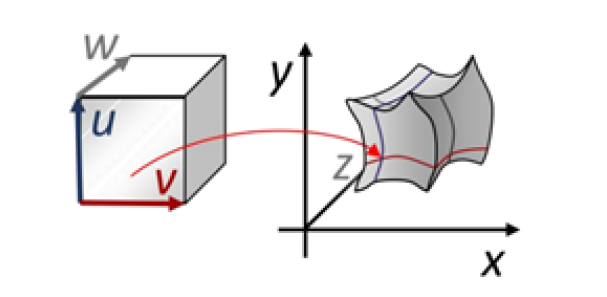
- 有限元方法
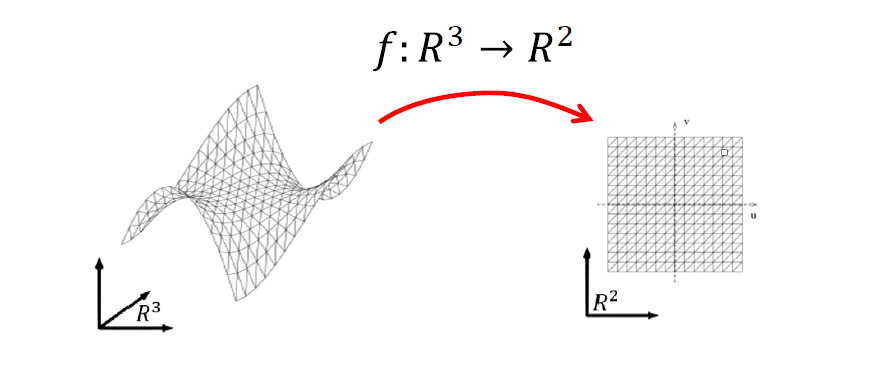
特例:降维映射(低维投影)
- 降维映射一般有信息丢失
- 丢失的信息大部分情况下不可逆,即无法恢复
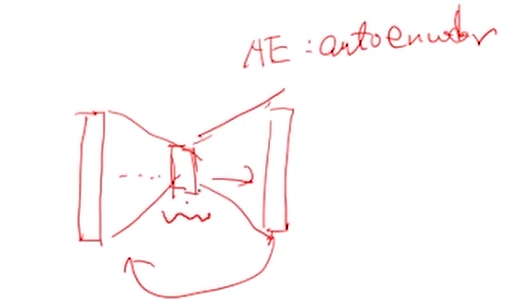
- AE:AutoEncoder 自编码器
- 先映射到低维度,再映射到高维度
- 要求中间层的最低维度不能低于原始的本征维度,否则无法复原
一般映射
- \(f:R^m\to R^n\)
- 如果 \(n<m\) ,为低维到高维的映射(高维的超曲面,n 维流形曲面),本征维度为 \(n\)
- 如果 \(n>m\),为降维映射
- 一般信息有损失
- 如果 \(R^n\) 中的点集刚好位于一个 m 维(或小于 m)的流形上,则映射可能是无损的,即可以被恢复的
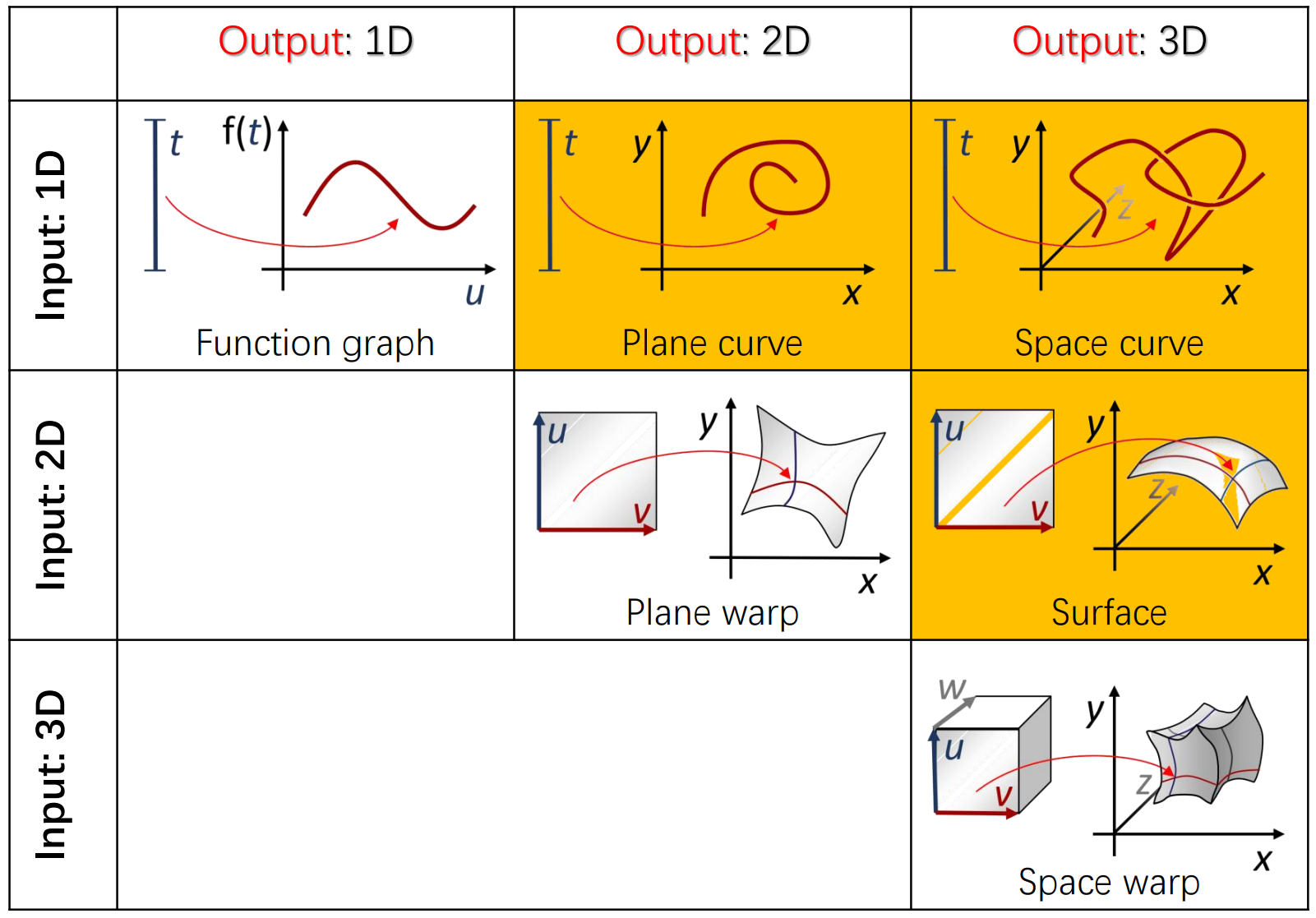
低维空间之间的函数
- 课程主要集中讨论橙色部分
曲线拟合
曲线拟合问题
- 非函数型
- 输入:给定平面上系列点 \((x_i,y_i),i=1,2,\cdots,n\)
- 输出:一条参数曲线,拟合这些点
- \(f:R^1\to R^2\)
\[ \left\{ \begin{array}{**lr**} x=x(t)\\ y=y(t)\\ \end{array} \right. t\in[0,1] \]
- 如果使用之前单变量的拟合方法,看成两个函数,用 \(x_i\) 去拟合 \(x(t)\),需要找到点对 \((t_i,x_i)\)
- 然而并没有这些点对,不能简单的这么做
- 现在相当于需要找每一个点对应的 \(t_i\)
- 参数化
转换
- 问题:对数据点 \((x_i,y_i)\),对应哪个参数 \(t_i\)?
- 矢量符号化表达
\[ \mathbf{p}=\mathbf{p}(t)= \begin{pmatrix} x(t)\\ y(t)\\ \end{pmatrix} \]
- 误差度量
\[ E=\sum_{i=1}^{n} \left\Vert \begin{pmatrix} x(t)\\ y(t)\\ \end{pmatrix} - \begin{pmatrix} x_i\\ y_i\\ \end{pmatrix} \right\Vert^2 = \sum_{i=1}^{n} \left\Vert \mathbf{p}(t)-\mathbf{p_i} \right\Vert^2 \]
参数化问题
- 求数据点所对应的参数:一个降维的问题
- 使用一组基函数(共享基函数)
\[ \left\{ \begin{array}{**lr**} x=x(t)=\sum(a_iB_i(t))\\ y=y(t)=\sum(b_iB_i(t))\\ \end{array} \right. t\in[0,1] \]
- 然后极小化误差度量:\(E\)
\[ E=\sum_{i=1}^{n}\left\Vert\mathbf{p}(t)-\mathbf{p_i}\right\Vert^2 \]
点列的参数化
- Equidistant (uniform) parameterization
- \(t_{i+1}-t_{i}\) 为常数 const
- 起始点为 0,终止点为 1
- 中间的点均匀划分,例如 n 个点,\(t_i=\dfrac{i}{n}\)
- Geometry of the data points is not considered(没有考虑数据的信息)
- \(t_{i+1}-t_{i}\) 为常数 const
- Chordal parameterization
- \(t_{i+1}-t_{i}=\Vert\mathbf{k}_{i+1}-\mathbf{k}_i\Vert\)
- 按照弦长去分配
- 可以归一化到 \([0,1]\) 之间
- Parameter intervals proportional to the distances of neighbored
control points
- 区间和弦长成正比
- \(t_{i+1}-t_{i}=\Vert\mathbf{k}_{i+1}-\mathbf{k}_i\Vert\)
- Centripetal parameterization
- \(t_{i+1}-t_{i}=\sqrt{\Vert\mathbf{k}_{i+1}-\mathbf{k}_i\Vert}\)
- Foley parameterization
- Involvement of angles in the control polygon(考虑边之间的夹角)
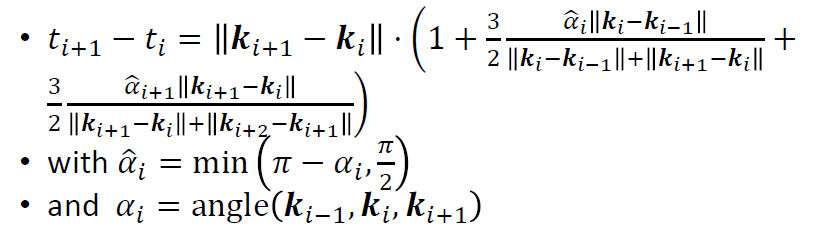
例子
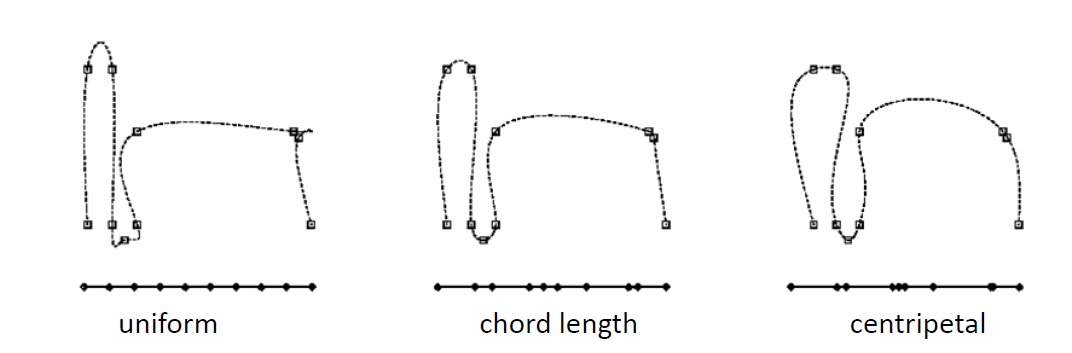
- 点的参数化对曲线拟合的影响很大,需要好的参数化
曲面的参数化
- 三维的点找二维的参数:一个降维的问题
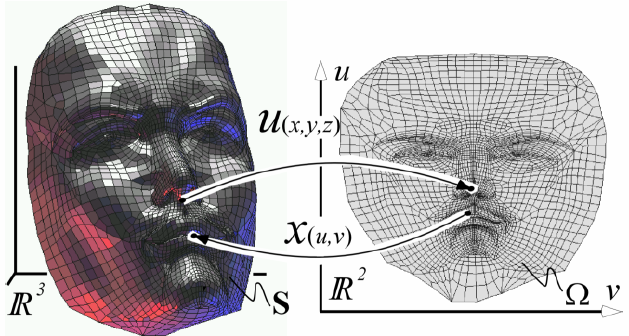
- 好的参数化:保持邻域内的几何结构
应用
- 地图绘制(地理学)
- 纹理映射
- uv 图
