GAMES102.刘利刚.01.数据拟合(Data Fitting)(02)
- https://www.bilibili.com/video/BV1NA411E7Yr
数据拟合
函数拟合问题
- 输入:一些观察(采样)的数据点 \(\{x_i,y_i\}_{i=0}^n\)
- 输出:你和数据点的函数 \(y=f(x)\),并用于预测
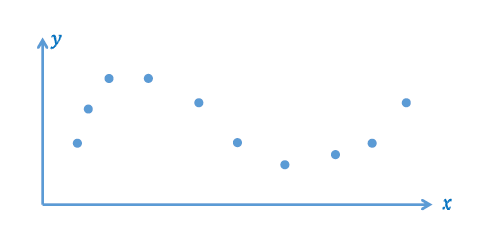
- 这样的拟合函数有无穷个
拟合函数的好坏评价
分段线性插值函数
- \(y=f_1(x)\)
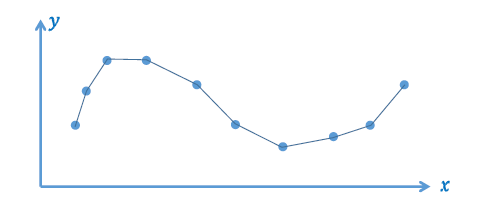
- 数据误差为 0
- 函数性质不够好
- 只有 \(C^0\) 连续,不光滑
- 一阶导数不连续
- 数值计算很麻烦
- 只有 \(C^0\) 连续,不光滑
光滑插值函数
- \(y=f_2(x)\)
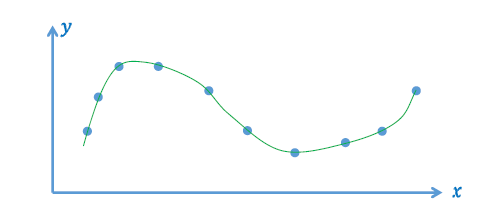
- 数据误差为 0
- 可能被 “差数据” 带歪,导致函数性质不好、预测不可靠
- 噪声,outliers(游离点)
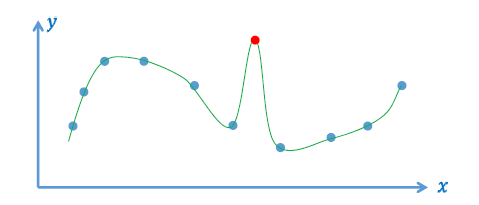
逼近拟合函数
- \(y=f_3(x)\)
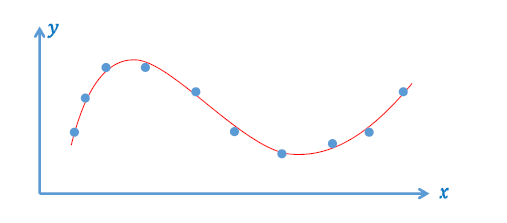
- 数据误差不为 0,但是足够小
- 能够抵抗一些 “差数据” 的影响
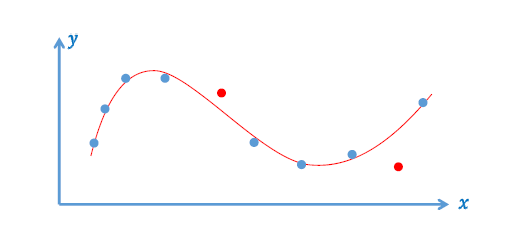
选择什么拟合函数
- 应用驱动,除非知道数据的先验,找到一个合适的拟合函数时一个比较复杂的过程
- 先验:领域知识
- 大部分的实际应用问题
- 可建模为:找一个映射/变换/函数
- 输入不一样、变量不一样、维数不一样
- 三步曲方法论:
- 到哪找?
- 确定某个函数集合/空间
- 找哪个?
- 度量哪个函数是好的 “最好” 的
- 怎么找?
- 求解或优化:不同的优化方法与技巧,既要快、又要好 ···
- 到哪找?
数据拟合的方法论
- 到哪找?
- 确定函数的表达形式(函数集、空间)
- \(L=span\{b_0(x),\cdots,b_n(x)\}\)
- 待定基函数的组合系数(求解变量)
- \(f_\lambda(x)=\sum_{k=0}^n\lambda_ib_i(x)\)
- 确定函数的表达形式(函数集、空间)
- 找哪个?
- 优化模型(最小化问题)
- 能量项 = 误差项 + 正则项
- 正则项
- \(\int |f''|^2\;\mathrm{d}x\) 度量光滑性
- \(\int \Vert \nabla f\Vert\;\mathrm{d}x\) 弧长尽量小
- 统计模型、规划模型 ···
- 优化模型(最小化问题)
- 怎么找?
- 求解误差函数的驻点(导数为 0 之处)
- 转化为系数的方程组
- 如果是欠定的(有无穷多组解),则修正模型
- 改进/增加 各种正则项:Lasso、岭回归、系数正则项 ···
- 返回修改模型
- 如果是欠定的(有无穷多组解),则修正模型
- 如果时非凸的、欠定的则变成难解问题
函数插值定义
- \(f(x)\) 为定义在区间 \([a, b]\) 上的函数,\(x_0, x_1,\cdots, x_n\) 为区间上 \(n+1\) 个互不相同的点,\(\Phi\) 为给定的某一函数类
- 求 \(\Phi\) 上的函数 \(\phi(x)\),满足:
\[ \phi(x_i)=f(x_i),\quad i=0,\cdots,n \]
- 则称 \(\phi(x)\) 为 \(f(x)\) 关于节点 \(x_0, x_1,\cdots, x_n\) 在 \(\Phi\) 上的插值函数
- 称 \(x_0, x_1,\cdots, x_n\) 为插值节点
- 称 \((x_i, f(x_i))\)为插值点
多项式插值
多项式插值定理
- 若 \(x_i\) 两两不同,则对任意给定的 \(y_i\),存在唯一的次数至多是 \(n\) 次的多项式 \(p_n\),使得 \(p_n(x_i)=y_i,\quad i = 0, \cdots,n\)
- 证明如下:范德蒙德行列式不为 0

技巧1:构造插值问题的通用解
- 如果每次都需要求解方程组,则比较麻烦
- 预先构造插值问题的通用解
- 给定 \(n+1\) 个点 \(\{(x_0,y_0),\cdots,(x_n,y_n)\}\),寻找一组次数为 \(n\) 的多项式基函数 \(l_i\) 使得
\[ l_i(x_j)=\left\{\begin{aligned} &1,\mathrm{if}\;i=j\\ &0,\mathrm{if}\;i\ne j \end{aligned}\right. \]
- 插值问题的解为
\[ P(x)=y_0l_0(x)+y_1l_1(x)+\cdots+y_nl_n(x)=\sum_{i=0}^{n}y_il_i(x) \]
怎么计算多项式 \(l_i(x)\)
- \(n\) 阶多项式,且有以下 \(n\) 个根
\[ x_0,x_1,\cdots,x_{i-1},x_{i+1},\cdots,x_n \]
- 故可表示为
\[ \begin{aligned} l_i(x)&=C_i(x-x_0)(x-x_1)\cdots(x-x_{i-1})(x-x_{i+1})\cdots(x-x_n)\\ &=C_i\prod_{i=0\land j\ne i}^{n}(x-x_j) \end{aligned} \]
- 由 \(l_i(x_i)=1\) 可以得到
\[ 1=C_i\prod_{i=0\land j\ne i}^{n}(x_i-x_j)\Rightarrow C_i=\dfrac{1}{\prod_{i=0\land j\ne i}^{n}(x_i-x_j)} \]
- 最终的多项式基函数为
\[ l_i(x)=\dfrac{\prod_{i=0\land j\ne i}^{n}(x-x_j)}{\prod_{i=0\land j\ne i}^{n}(x_i-x_j)} \]
- \(l_i(x)\) 被称为拉格朗日多项式
技巧2:更方便的求解表达
- Newton 插值:具有相同 “导数”(差商)的多项式构造(n 阶 Taylor 展开)
差商定义
- 一阶差商
\[ f[x_0,x_1]=\dfrac{f(x_1)-f(x_0)}{x_1-x_0} \]
- k 阶差商
- 设 \(\{x_0,x_1,\cdots,x_n\}\) 互不相同,\(f(x)\) 关于 \(\{x_0,x_1,\cdots,x_n\}\) 的 k 阶差商如下
\[ f[x_0,\cdots,x_{k}]=\dfrac{f[x_1,\cdots,x_{k}]-f[x_0,\cdots,x_{k-1}]}{x_k-x_0} \]
- 所以 Newton 插值多项式表示为
\[ N_n(x)=f(x_0)+f[x_0,x_1](x-x_0)+\cdots+f[x_0,\cdots,x_n](x-x_0)\cdots(x-x_{n-1}) \]
- 有一点巧妙
多项式插值存在的问题
- 系数矩阵稠密
- 依赖于基函数选取,矩阵可能病态,导致难于求解(求逆)
病态矩阵举例
- 对于扰动很敏感
- 对于如下方程组
\[ \left\{\begin{aligned} &x_1+0.5x_2=1.5\\ &0.667x_1+0.333x_2=1\\ \end{aligned}\right. \Rightarrow \left\{\begin{aligned} &x_1=1\\ &x_2=1\\ \end{aligned}\right. \]
- 对等式右边进行扰动 0.001
\[ \left\{\begin{aligned} &x_1+0.5x_2=1.5\\ &0.667x_1+0.333x_2=0.999\\ \end{aligned}\right. \Rightarrow \left\{\begin{aligned} &x_1=0\\ &x_2=3\\ \end{aligned}\right. \]
- 对系数矩阵进行扰动 0.001
\[ \left\{\begin{aligned} &x_1+0.5x_2=1.5\\ &0.667x_1+0.334x_2=1\\ \end{aligned}\right. \Rightarrow \left\{\begin{aligned} &x_1=2\\ &x_2=-1\\ \end{aligned}\right. \]
病态问题
- 输入数据的细微变化导致输出(解)的剧烈变化
- 将线性方程看成直线(超平面)
- 当系统病态时,直线变为近似平行
- 求解(即直线求交)变得困难、不精确
矩阵条件数
- 通过矩阵条件数刻画病态程度
\[ \kappa_2(A)=\dfrac{\max_{x\ne0}\dfrac{\Vert Ax\Vert}{\Vert x\Vert}}{\min_{x\ne0}\dfrac{\Vert Ax\Vert}{\Vert x\Vert}} \]
- 等于最大特征值和最小特征值之间比例
- 条件数大意味着基元之间有太多相关性
多项式插值问题是病态的
- 对于等距分布的数据点 \(x_i\),范德蒙矩阵的条件数随着数据点数 \(n\) 呈指数级增长
- 多项式最高次数为 \(n-1\)
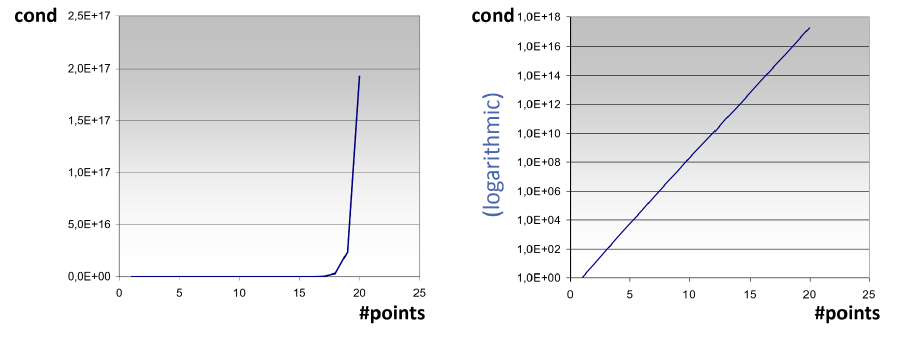
幂函数带来的问题
- 幂(单项式)函数基
- 幂函数之间差别随着次数增加而减小
- 不同幂函数之间唯一差别为增长速度(\(x^i\) 比 \(x^{i-1}\) 增长快)
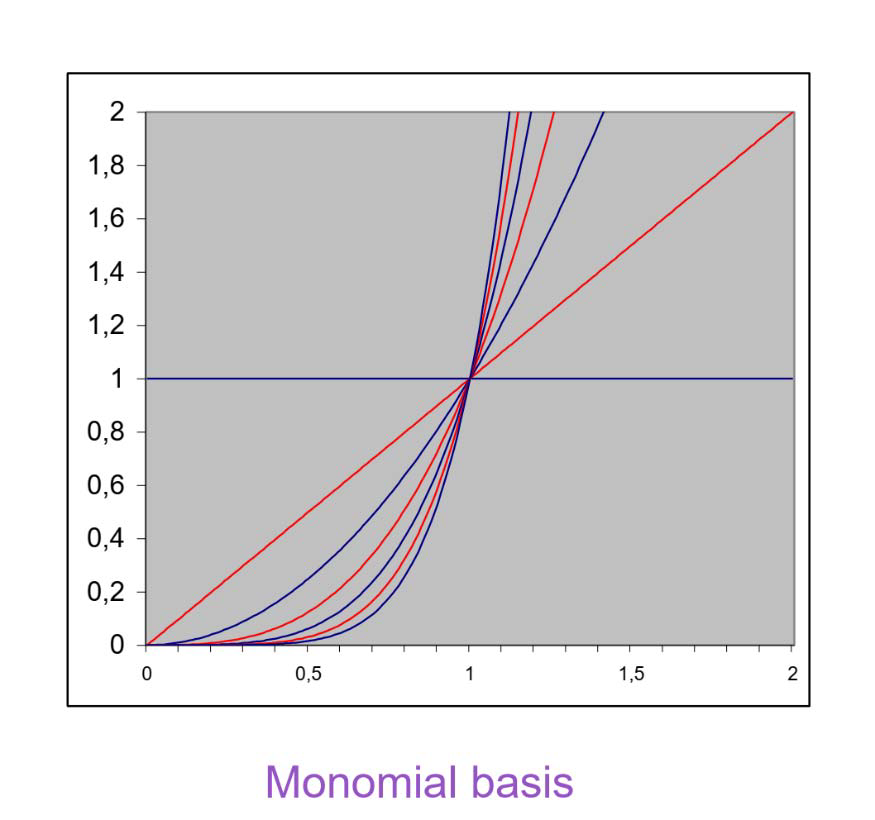
- 单项式
- 从左往右
- 首先常数 1 主宰
- 接着 \(x\) 增长最快
- 接着 \(x^2\) 增长最快
- ···
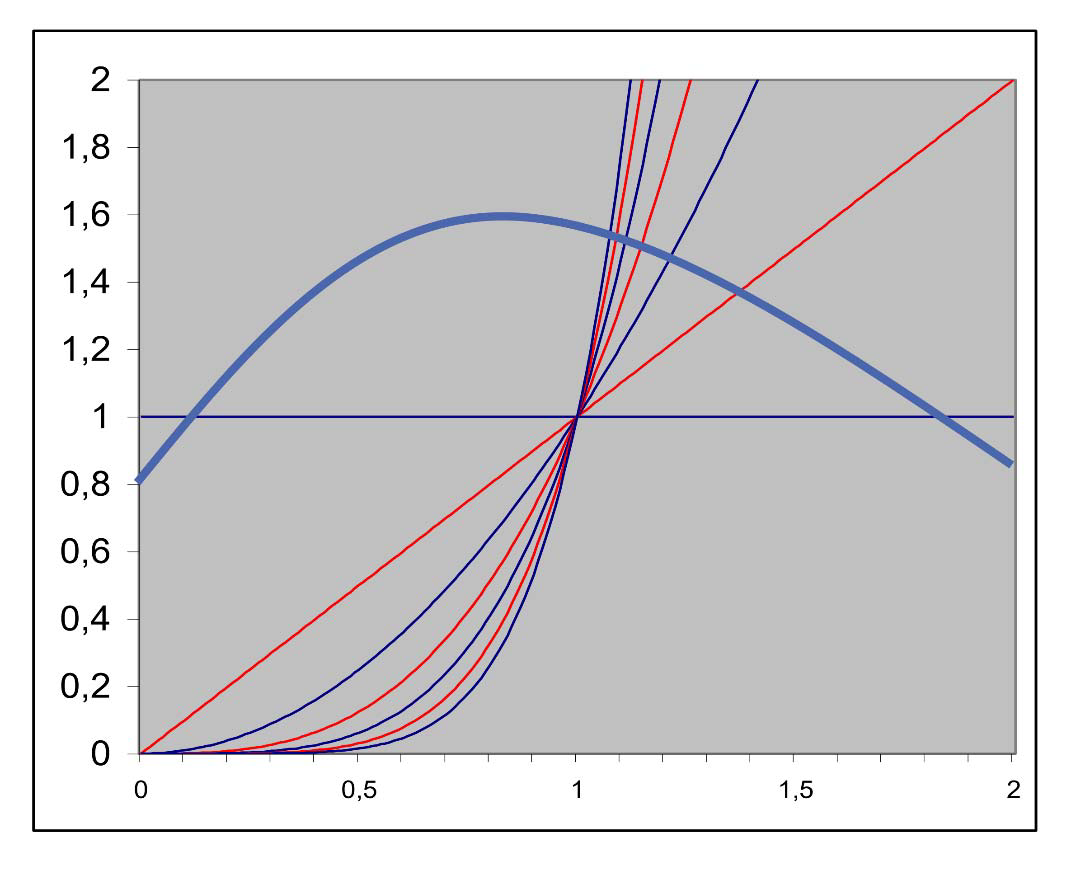
- 趋势
- 好的基函数一般需要系数交替
- 互相抵消问题
解决方法
- 使用正交多项式基
- 如何获得?
- Gram‐Schmidt 正交化
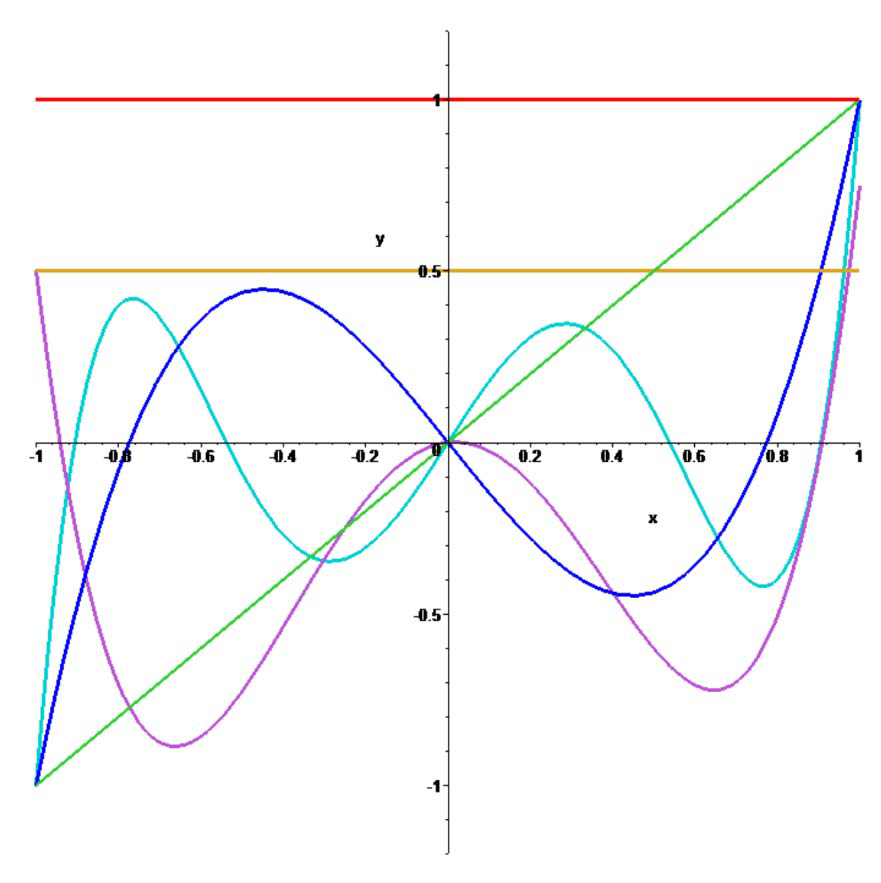
多项式插值结果
- 振荡(龙格 Runge)现象和对插值点数的高度敏感性
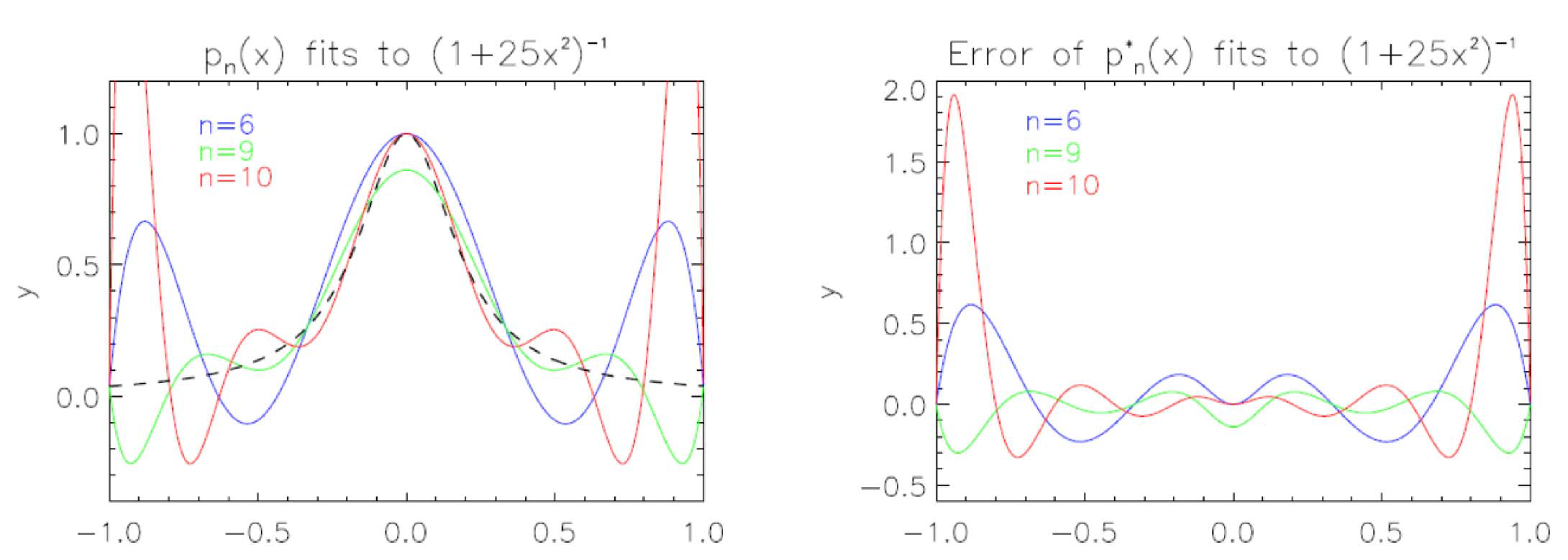
结论
- 多项式插值不稳定
- 控制点的微小变化可导致完全不同的结果
- 振荡(Runge)现象
- 多项式随着插值点数(可以是细微)增加而摆动
- 需要更好的基函数来做插值
- Bernstein 基函数
- 分片多项式
多项式逼近
为什么逼近
- 数据点含噪声、outliers 等
- 更紧凑的表达
- 计算简单、更稳定
最小二乘逼近
逼近问题
- 给定一组线性无关的连续函数集合 \(B=\{b_1,\cdots,b_n\}\) 和一组节点 \(\{(x_1,y_1),\cdots,(x_m,y_m)\}\)
- 其中 \(m\ge n\)
- 在 B 张成空间中那个函数 \(f\in span\{B\}\) 对节点的逼近最好
- 示例:给定一组点,找到最佳逼近的线性函数
- 怎么定义 “最佳逼近”?
最小二乘逼近
\[ \mathop{\arg\min}_{f\in span\{B\}}\sum_{j=1}^{m}\Big(f(x_j)-y_j\Big)^2 \]
- 系数 \(\lambda_1,\cdots,\lambda_n\)
\[ M=\left( \begin{aligned} b_1(x_1)\quad&\cdots\quad b_n(x_1)\\ \cdots\quad&\cdots\quad\cdots\\ b_1(x_n)\quad&\cdots\quad b_n(x_n)\\ \end{aligned} \right) \]
- 转化
\[ \begin{aligned} \sum_{j=1}^{m}\Big(f(x_j)-y_j\Big)^2&=\sum_{j=1}^{m}\Big(\sum_{i=1}^{n}\lambda_ib_i(x_j)-y_j\Big)^2\\ &=(M\lambda-y)^T(M\lambda-y)\\ &=\lambda^TM^TM\lambda-y^TM\lambda-\lambda^TM^Ty+y^Ty\\ &=\lambda^TM^TM\lambda-2y^TM\lambda+y^Ty \end{aligned} \]
求解
- 怎么求 \(\lambda\)
- 关于 \(\lambda\) 的二次多项式
\[ \lambda^TM^TM\lambda-2y^TM\lambda+y^Ty \]
- 法方程,最小解满足
- 求导即可
\[ M^TM\lambda=y^TM \]
- 转化为最小化二次目标函数
- 最小化二次目标函数 \(x^TAx+b^Tx+c\)
- 充要条件:\(2Ax=-b\)
函数空间及基函数
为什么用多项式
- 易于计算,表现良好,光滑
- 稠密性与完备性
- 表达能力足够
- 维尔斯特拉斯定理 (Weierstrass)
维尔斯特拉斯定理
- 令 \(f\) 为闭区间 \([a,b]\) 上的任意连续函数,则对任意给定的 \(\epsilon\),存在 \(n\) 会让多项式 \(P_n\) 满足
\[ \vert f(x)-P_n(x) \vert<\epsilon,\forall x\in[a,b] \]
- 定理只证明了存在性,未给出多项式
- 实际应用中 \(n\) 需要通过尝试确定
伯恩斯坦多项式
- 用 Bernstein 多项式做逼近
- 对 \([0,1]\) 区间上任意连续函数 \(f(x)\) 和任意正整数 \(n\),以下不等式对所有的 \(x\in[0,1]\) 成立
\[ \vert f(x)-B_n(f,x) \vert<\dfrac{9}{4}m_{f,n} \]
- \(m_{f,n}\) 如下
\[ m_{f,n}=\mathrm{lower\;upper\;bound}\vert f(y_1)-f(y_2)\vert \]
\[ y_1,y_2\in[0,1]\land\vert y_1-y_2\vert<\dfrac{1}{\sqrt{n}} \]
- \(B_n(f,x)\) 如下,其中 \(x_j=\dfrac{j}{n}\) 为 \([0,1]\) 上的等距采样点
\[ B_n(f,x)=\sum_{j=0}^{n}f(x_j)b_{n,j}(x) \]
- 伯恩斯坦多项式如下
\[ b_{n,j}={n\choose j}x_j(1-x)^{n-j} \]
- 不同次数的伯恩斯坦多项式的基空间
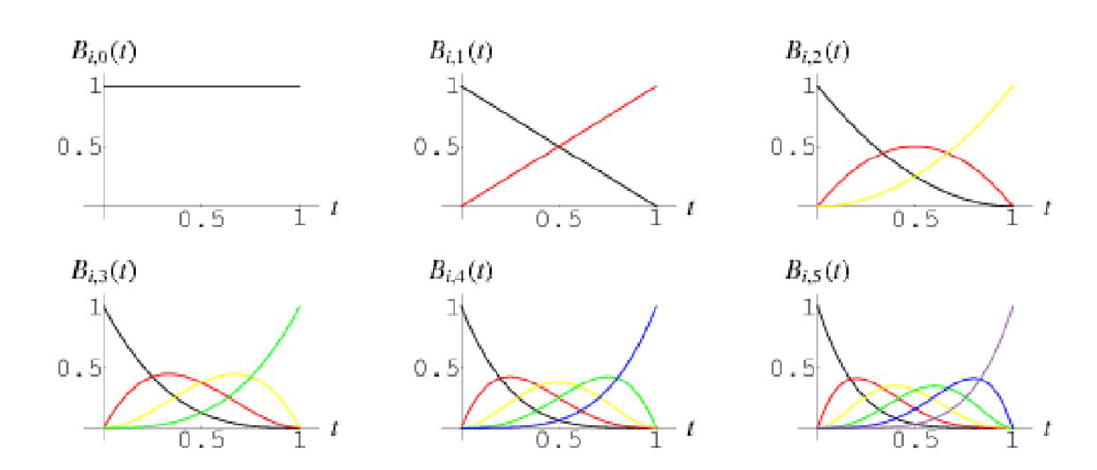
- 矩阵:不同的基函数空间的变换
用 Bernstein 多项式做逼近
- Bernstein 基函数的良好性质:非常好的几何意义!
- 正性、权性(和为1)\(\to\) 凸包性
- \(b_{n,j}>0\)(非边界)
- \(\sum_{j} b_{n,j}(x)=1\)
- 变差缩减性
- 递归线性求解方法
- 细分性
- ···
- 正性、权性(和为1)\(\to\) 凸包性
- Bernstein多项式逼近示例
- 逼近结果优秀
- 需要高阶
- 丰富的理论:CAGD 课程(计算机辅助几何设计)
Bernstein 函数
\[ B_n(f,x)=\sum_{j=0}^{n}f(\dfrac{j}{n})b_{n,j}(x) \]
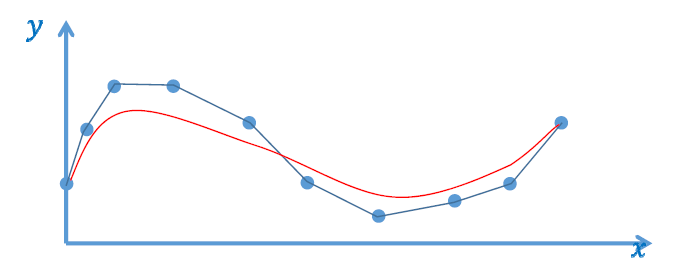
- 蓝色为采样点,红色线为 Bernstein 多项式拟合出来的结果
- 当 \(n\to\infty\),即采样点足够多的时候,\(B_n(f,x)\) 一致收敛到 \(f(x)\)
两种观点
- 代数观点
- 权性
- 把 \(f(\dfrac{i}{n})\) 看作是一系列的点,\(b_{n,f}(x)\) 对其进行加权,得到新的点
- 几何观点
- \(b_{n,f}(x)\) 是一系列的函数,使用系数 \(f(\dfrac{i}{n})\) 去组合它,得到新的函数
- 这两种观点可以用于之后的交互式设计控制顶点、曲线的设计
RBF 函数插值/逼近
- 低维中叫高斯函数
高斯函数
- Gauss
- 两个参数:均值 \(\mu\),方差 \(\sigma\)
\[ g_{\mu,\sigma}(x)=\dfrac{1}{\sqrt{2\pi}}\;\exp\left(-\dfrac{(x-\mu)^2}{2\sigma^2}\right) \]
- 几何意义
- \(\mu\):位置
- \(\sigma\):支集宽度
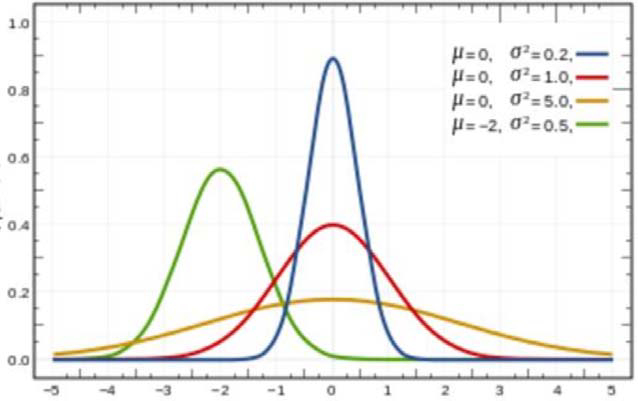
- 标准高斯函数
\[ g_{0,1}=\dfrac{1}{\sqrt{2\pi}}\;\exp\left(-\dfrac{x^2}{2}\right) \]
- 不同均值和方差的高斯函数都线性无关
- 可以作为一组基函数
RRF 函数拟合
- RBF 函数
\[ f(x)=b_0+\sum_{i=1}^{n}b_ig_i(x) \]
- 一个通用的方法
- 给定一些采样点,在这些采样点的周围放置一些基函数
- 待定系数,求导得出结果
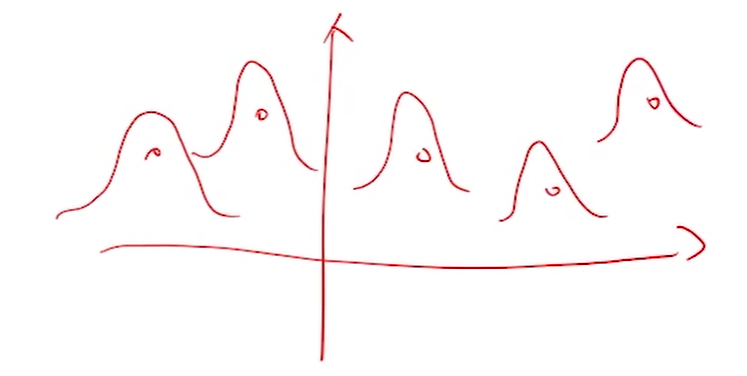
- 一些问题
- 需要人为选取 \(\mu,\sigma\)
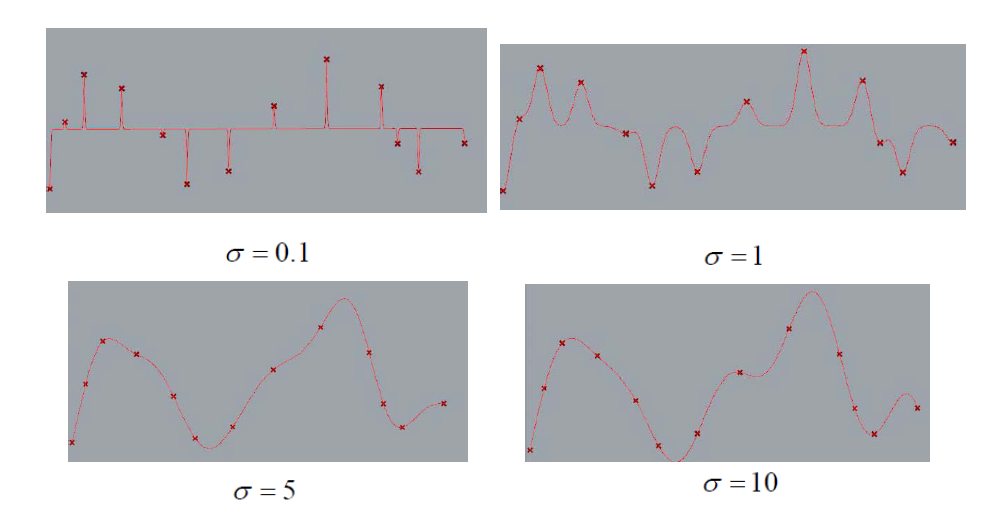
- 怎么控制选取 \(\mu,\sigma\)
- 能否将 \(\sigma,\mu\) 一起来优化?
- 可以的
- 能否将 \(\sigma,\mu\) 一起来优化?
从另一个角度来看拟合函数
Guass 拟合函数
- 一般 Gauss 函数表达为标准 Gauss 函数的形式
\[ \begin{aligned} g_{\mu,\sigma}(x)&=\dfrac{1}{\sqrt{2\pi}}\;\exp\left(-\dfrac{(x-\mu)^2}{2\sigma^2}\right)\\ &=\dfrac{1}{\sqrt{2\pi}}\;\exp\left(-\dfrac{1}{2}\left(\dfrac{x}{\sigma}-\dfrac{\mu}{\sigma}\right)^2\right)\\ &=g_{0,1}(\dfrac{1}{\sigma}x-\dfrac{\mu}{\sigma})\\ &=g_{0,1}(ax+b)\\ \end{aligned} \]
- 将上面的函数进行转化
- 此时可以同时优化 \(\mu,\sigma\)
\[ f(x)=b_0+\sum_{i=1}^{n}b_ig_i(x) \]
\[ f(x)=\omega_0+\sum_{i=1}^{n}\omega_ig_{0,1}(a_ix+b_i) \]
基函数是由一个基本函数通过平移和伸缩变换而来的
理论上可以证明:\(a_i,b_i\) 足够多,上述多项式也能逼近所有的函数
换个方式看函数:神经网络
- 将Gauss函数看成网络
- \((x,1)\) 是齐次坐标的用法,可以把平移也结合进去
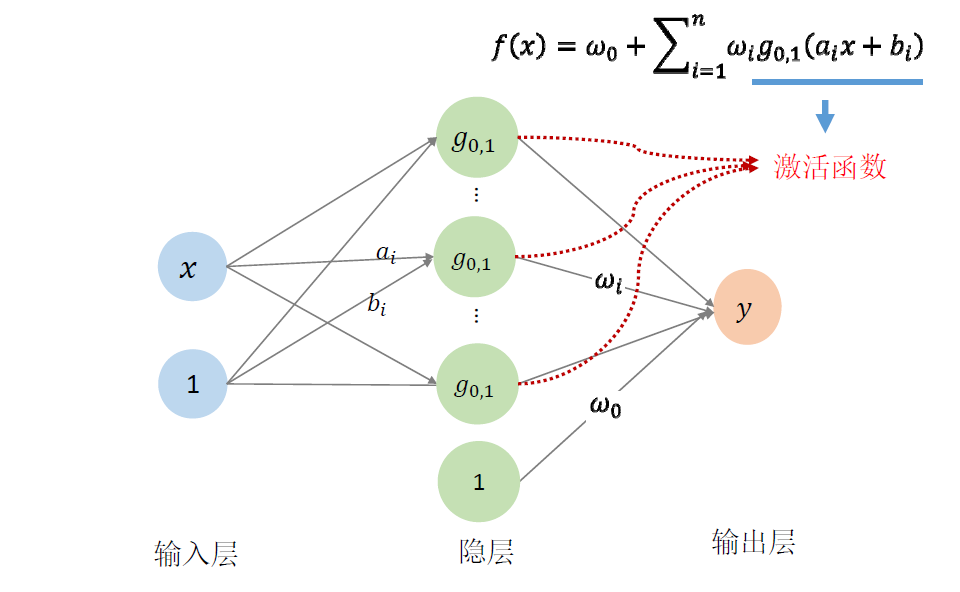
- 这就是 RBF 网络
- \(n\) 对应隐层结点个数,激活函数是标准高斯函数
抽象:神经元
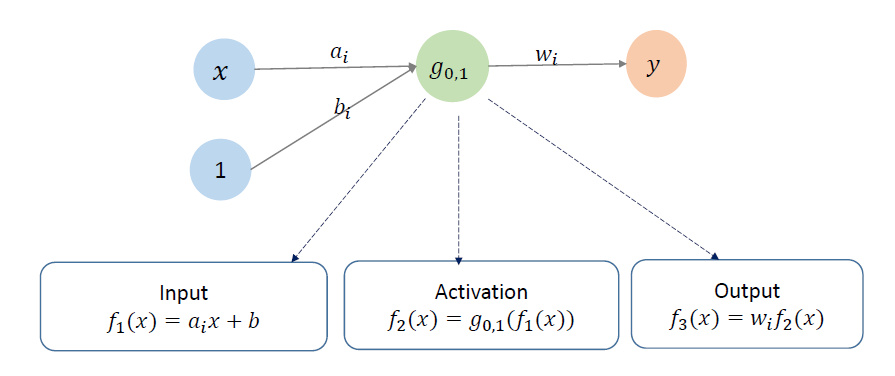
RBF 神经网络
- 高维情形:RBF (Radial Basis Function),径向基函数
- 一种特殊的 BP 网络
- 优化:BP 算法
- 反向传播
- 优化:BP 算法
- 核函数思想
- Gauss 函数的特性:拟局部性
- 求 \(a_i,b_i\)时候需要求导,结果是非线性非凸的,很难求出极值
- 落入局部极值
- 初值选取很重要
- 神经网络就是一个函数
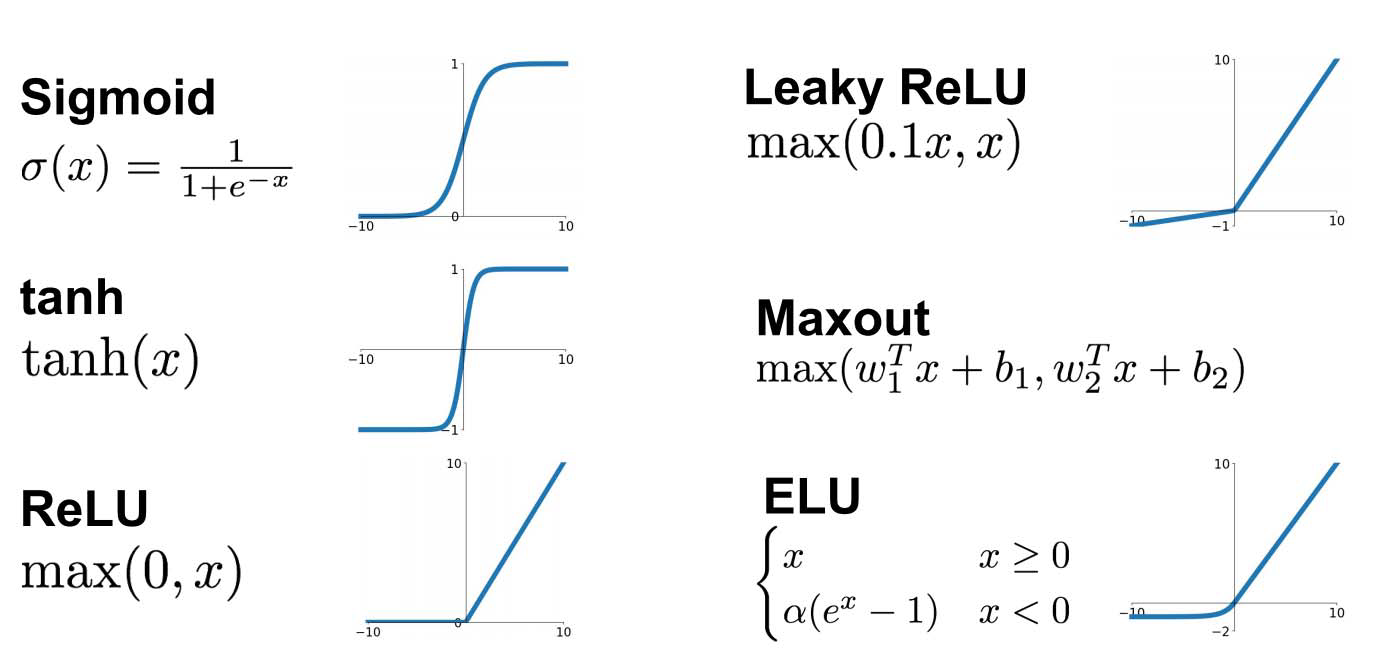
思考:激活函数的选择
- 启发:由一个简单的函数通过(仿射)变换构造出一组基函数,张成一个函数空间
- 表达能力是否足够强:是否完备/稠密的?
高维情形:多元函数
- 每一个神经元的输入是 \((x_1,\cdots,x_n)\) 的齐次坐标 \((x_1,\cdots,x_n,1)\)
- 变量的多个分量的线性组合: \(g_{0,1}(a_i^1x_1+\cdots+a_n^ix_n+b_i)\)
- 单隐层神经网络函数
\[ f(x_1,\cdots,x_n)=\omega_0+\sum_{i=1}^{n}w_ig_{0,1}(a_i^1x_1+\cdots+a_n^ix_n+b_i) \]
多层神经网络
- 单层
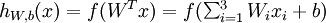
- 多层
- 线性函数和非线性函数的多重复合
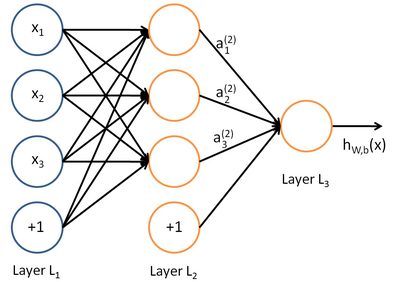
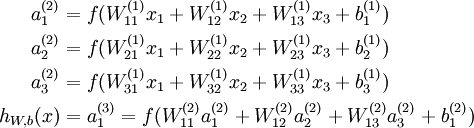
用神经网络函数来拟合数据
- 回归问题
- Regression problem:
- Input: Given training set (x1, y1), (x2, y2), (x3, y3 ),...
- Output: Adjust parameters \(\theta\) (for every node) to make: \(h(x_i)\approx y_i\)
万能逼近定理:自由度足够多
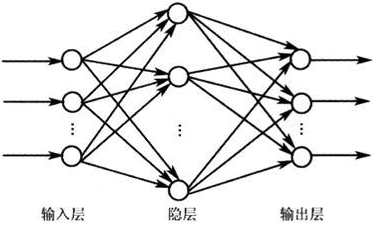
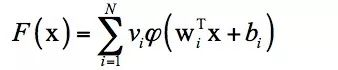
- 与传统拟合一样存在同样的问题:函数个数如何选?
- 调参
使用深度学习的方法
- 问题建模
- 理解问题、问题分解(多个映射级联)、…
- 找哪个?
- 损失函数、各种 Penalty、正则项、…
- 到哪找?
- 神经网络函数、网络简化、···
- 怎么找?
- 优化方法(BP方法)
- 初始值、参数、···
- 调参:有耐心、有直觉、···