GAMES102.刘利刚.01.数据拟合(Data Fitting)

Posted on Edited on In Views:
一些数学基础、拟合问题的三部曲（到哪找、找哪个、怎么找）、正则项
  • https://www.bilibili.com/video/BV1NA411E7Yr

数据拟合

数学基础

  • 科学研究过程
    • 问题 \(\to\) 模型、算法、代码
  • 数学语言：抽象的思维

集合

  • 集合
  • 基数
  • 有限集、无限集
  • 可数集、不可数集
  • 集合运算：并、交、差

线性空间

  • 元素之间有运算：加法、数乘
  • 线性结构：对加法和数乘封闭
    • 加法交换律、结合律，数乘分配律，···
  • 基 / 维数：\(L=span\{V_1,V_2,\cdots,V_n\}=\{\sum_{i}^{n}a_iV_i\vert a_i\in R\}\)
    • 每个元素表达为 n 个实数，即一个向量 \((a_1,a_2,\cdots,a_n)\)
  • 例子
    • 欧氏空间：1D实数、2D平面、3D空间、···
    • n 次多项式：\(f(x)=\sum_{k=0}^{n}a_kx^k\)

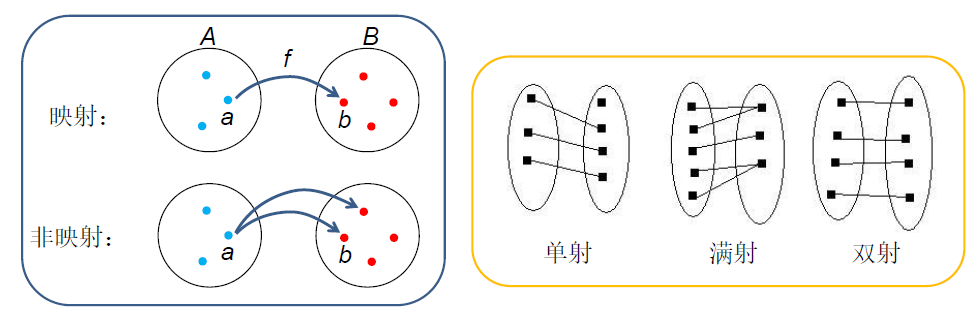
映射

  • 两个非空集合 \(A\) 和 \(B\) 的映射 \(f:A\to B\)
    • 对 \(A\) 中的任何一个元素 \(a\)，有唯一的一个 \(B\) 中的元素 \(b\) 与之对应，记为 \(f(a)=b\)
    • \(b\) 称为 \(a\) 的象，\(a\) 称为 \(b\) 的原象
    • \(A\) 称为定义域，\(\{b\vert\exists a\in A(f(a)=b)\}\) 称为值域

函数

  • 非空实数集之间的映射称为（一元）函数 \(y=f(x)\)，或变换
    • \(f:R^1\to R^1\)
  • 函数的图像（可视化）：所有的有序数对 \((x,y)\) 组成的集合

函数的集合

  • 函数空间
  • 用若干简单函数（“基函数”）线性组合张成一个函数空间
  • \(L=span\{f_1,f_2,\cdots,f_n\}=\{\sum_{i}^{n}a_if_i(x)\vert a_i\in R\}\)
  • 每个函数就表达（对应）为 n 个实数，即系数向量 \((a_1,a_2,\cdots,a_n)\)
  • 多项式函数空间（幂基）

\[ f(x)=\sum_{k=0}^{n}w_kx^k \]

  • 三角函数空间（三角函数基）

\[ f(x)=a_0+\sum_{k=1}^{n}(a_k\cos kx+b_k\sin kx) \]

  • 函数空间的完备性
    • 这个函数空间是否可以表示（逼近）任意函数
  • 泛函分析

赋范空间

  • 内积诱导范数、距离

\[ \langle f,g\rangle=\int_{a}^{b}f(x)g(x)\;\mathrm{d}x \]

  • 度量空间：可度量函数之间的距离
    • Lp 范数
  • 赋范空间 + 完备性 = 巴拿赫空间
  • 内积空间（无限维）+ 完备性 = 希尔伯特空间

万能逼近定理

  • Weierstrass 逼近定理
    • 定理1：闭区间上的连续函数可用多项式级数一致逼近
    • 定理2：闭区间上周期为 \(2\pi\) 的连续函数可用三角函数级数一致逼近

傅里叶级数

\[ f(t)=A_0+\sum_{n=1}^{n}(a_n\cos(n\omega t)+b_k\sin(n\omega t)) \]

\[ f(t)=A_0+\sum_{n=1}^{n}(A_n\sin(n\omega t+\psi_n)) \]

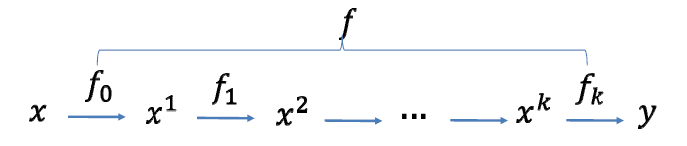
函数复合

\[ f=f_k\circ f_{k-1}\circ\cdots\circ f_0 \]

如何求满足要求的函数

  • 大部分的实际应用问题
    • 可建模为：找一个映射/变换/函数
    • 输入不一样、变量不一样、维数不一样
  • 如何找函数的三步曲
    • 到哪找？
      • 确定某个函数集合/空间
    • 找哪个？
      • 度量哪个函数是好的/“最好”的
    • 怎么找？
      • 求解或优化：不同的优化方法与技巧，既要快、又要好

逆向工程

  • 求船型曲线
  • 已知：某条船的侧面投影曲线图
  • 求：该投影轮廓线的表达函数？
  • 方法
    • 从投影曲线上描（采样）一系列点
    • 找一个函数拟合这些采样点

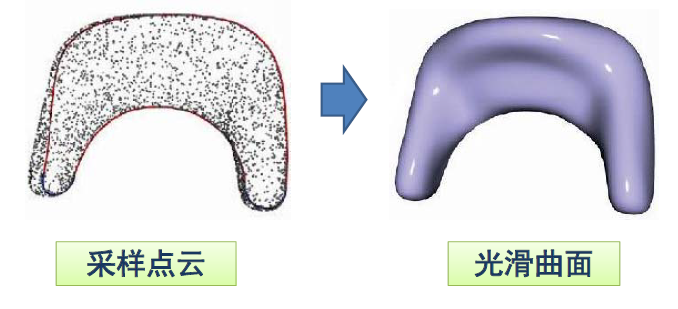
曲线 / 曲面拟合

  • 输入：一些型值（采样）点集
  • 输出：一条拟合这些点集的曲线 / 曲面

函数拟合

拟合问题

  • 输入：一些观察的数据点
  • 输出：反映这些数据规律的函数 \(y=f(x)\)
    • 暂时限制 \(x\in R^1,y\in R^1\)
  • 拟合问题三部曲：到哪找、找哪个、怎么找

(1) 到哪找

  • 选择一个函数空间
    • 线性函数空间 \(A=span\{B_0(x),\cdots,B_n(x)\}\)
      • 多项式函数
      • RBF 函数
      • 三角函数
  • 函数表达

\[ f(x)=\sum_{k=0}^{n}a_kB_k(x) \]

  • 确定 \(n+1\) 个系数 \((a_0,\cdots,a_k)\)
    • 待定系数法

(2) 找哪个

  • 确定一个损失函数（目标）
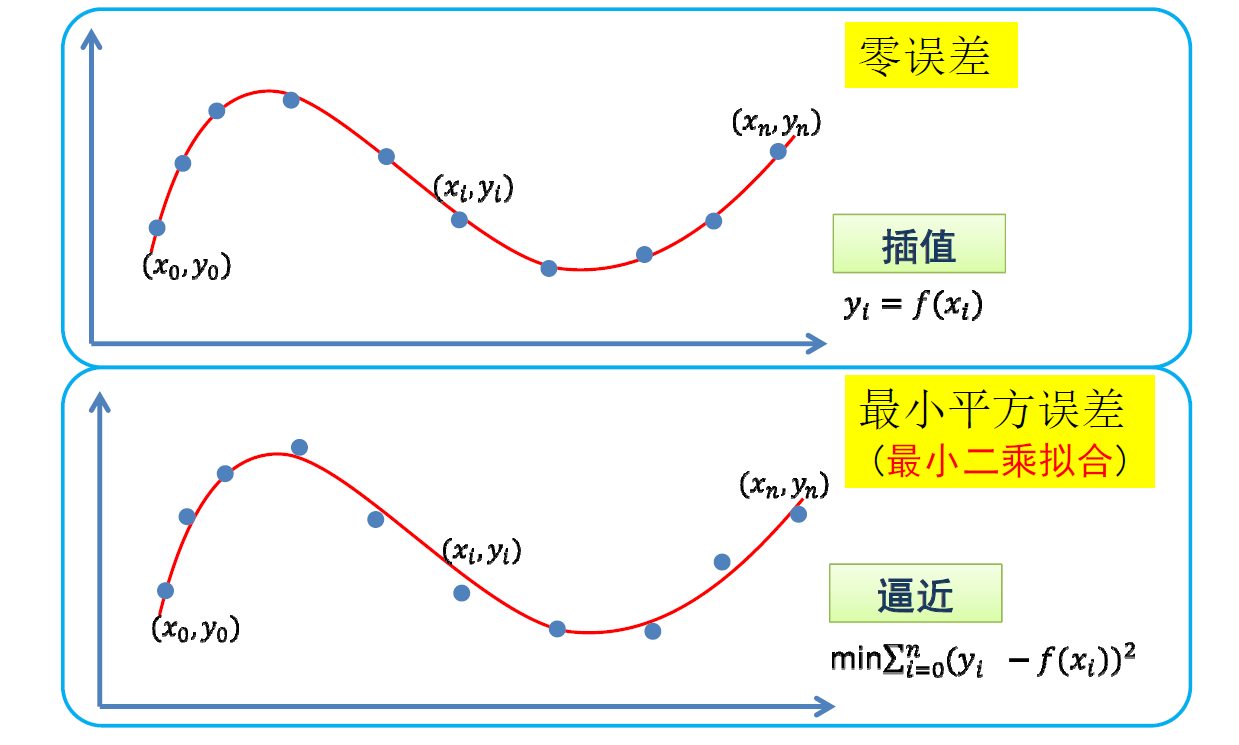
[1] 插值
  • 函数经过每个数据点
  • 零误差
[2] 逼近
  • 函数尽量靠近数据点
  • 例如：平方和误差（比较好求解）

\[ \min\sum_{i=0}^{n}(y_i-f(x_i))^2 \]

(3) 怎么找

[1] 插值
  • 联立求解线性方程组

\[ y_i=f(x_i)=\sum_{i=0}^{n}a_kB_k(x_i),\qquad i=0,1,\cdots,n \]

  • 求解 \((n+1)\times(n+1)\) 线性方程组
  • \(n\) 次拉格朗日插值多项式
  • 病态问题
    • 系数矩阵条件数高时，求解不稳定
n 阶拉格朗日插值多项式
  • 插值 n+1 个点、次数不超过 n 的多项式是存在而且是唯一的
    • n+1个变量，n+1个方程
  • 插值函数的自由度 = 未知量个数 - 已知量个数
[2] 逼近

\[ \min\sum_{i=0}^{n}(y_i-f(x_i))^2 \]

  • 最小二乘法
  • 对各系数求导，得到一个线性方程组（法方程 normal equation）
  • \(AX=b\)
  • 实际应用一般都是使用逼近的方法，采集到的数据可能会有误差
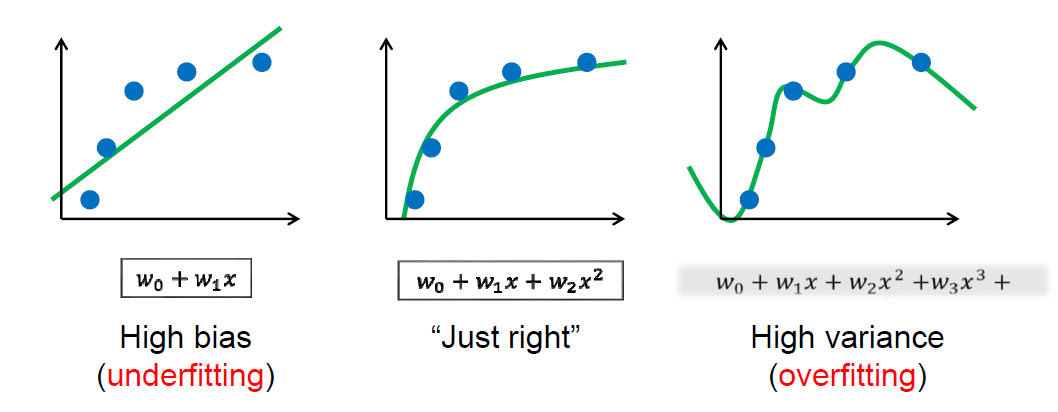
  • 问题：怎么选择多项式次数是一个比较难的问题
    • 点多，系数少：表达能力不够
    • 点少，系数多：过拟合

插值 vs 逼近

过拟合与欠拟合

  • 过拟合（overfitting）
    • 交叉验证

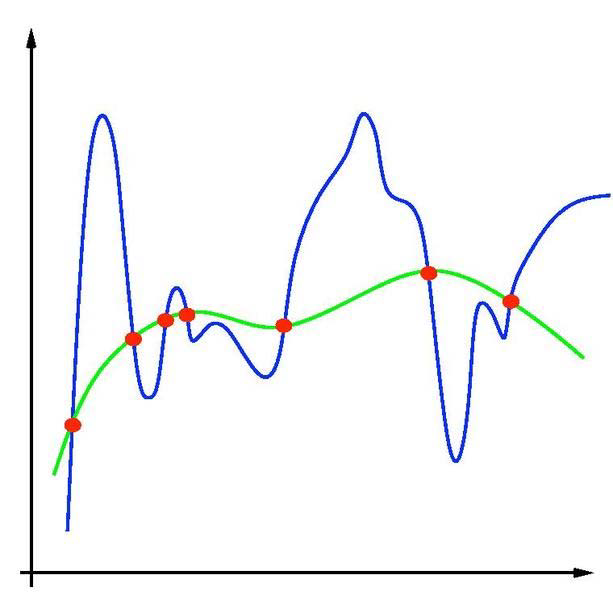
  • 欠拟合

  • 需要根据不同的应用与需求，不断尝试（不断 “调参”）

避免过拟合的常用方法

  • 数据去噪
    • 剔除训练样本中噪声
  • 数据增广
    • 增加样本数，或者增加样本的代表性和多样性
      • 让采样可能性小的点也能够被采到
  • 模型简化
    • 预测模型过于复杂，拟合了训练样本中的噪声
    • 选用更简单的模型，或者对模型进行裁剪
  • 正则约束
    • 适当的正则项，比如方差正则项、稀疏正则项

正则项

岭回归正则项

  • 选择一个函数空间
    • 基函数的线性表达
    • \(W=(w_0,w_1,\cdots,w_n)\)

\[ y=f(x)=\sum_{i=0}^{n}w_iB_i(x) \]

  • 最小二乘拟合

\[ \min_{W}\Vert Y-XW\Vert^2 \]

  • Ridge regression （岭回归）

\[ \min_{W}\Vert Y-XW\Vert^2+\mu\Vert W\Vert_2^2 \]

  • 让回归问题变得更加稳定

稀疏学习：稀疏正则化

  • 冗余基函数（过完备）
  • 通过优化来选择合适的基函数
    • 系数向量的 \(L_0\) 模（非0元素个数）尽量小
      • 让选择的基函数越少越好
    • 挑选（“学习”）出合适的基函数
  • 两种等价表示形式

\[ \min_{\alpha}\Vert Y-XW\Vert^2+\mu\Vert W\Vert_0 \]

\[ \min_{\alpha}\Vert Y-XW\Vert^2,\quad s.t.\;\Vert W\Vert_0\le\beta \]

压缩感知

  • \(M << N\)

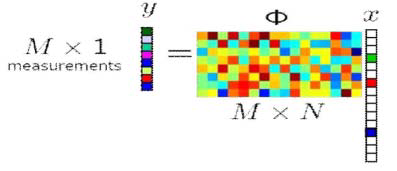
  • 已知 \(y\) 和 \(\Phi\) ，有无穷多解 \(x\)
  • 对于稀疏信号 \(x\)，可通过优化能完全重建 \(x\)
    • 在一定条件下（\(\Phi\)）[Candes and Tao 2005]
  • \(L_0\) 优化

\[ \min\Vert x\Vert_0,\quad s.t.\;\Phi x=y \]

思考

  • 非函数型的曲线拟合
    • 分段（怎么保证连接点光滑）
  • 高维函数的拟合