数据结构与算法.宋国杰.01.引言与概论

引言

课程目标

• 逻辑结构
  • 图 \(\supseteq\) 树 \(\supseteq\) 线性
• 存储结构
  • 顺序、链接
  • 索引、散列
• 运算
  • 增删查改
  • 遍历、排序
• 时间复杂度 vs 空间复杂度
  • trade off

解决问题的过程

• 问题（Problem Problem ）
  • 从输入到出的一种函数映射
• 数据结构（Data Structure）
  • 数据的逻辑结构及在计算机中存储表示 ，以及相应操作
• 算法（Algorithm）
  • 对特定问题求解过程的描述 方法
• 程序（Program）
  • 算法在计机程序设语言中的实现

概论

数据结构

• 涉及数据之间的逻辑关系、数据在计算机中的存储表示和在这种结构上一组能执行的操作（运算）
• 三要素
  • 逻辑结构、存储（物理）结构、运算

逻辑结构

• Logical Structure
• 具体问题的数学抽象，反映事物组成和逻辑关系

逻辑结构的表示

• 用一组数据（表示为结点集合 K），及数据间的二元关系（关系集合 R）表示：(K, R)
• K 由有限个结点组成，代表一组有明确结构的数据集
• R 是定义在集合 K 上的一组关系，每个关系 r \(\in\) R 都是 K\(\times\)K 上的二元关系，描述结点间的逻辑关系

结点的类型

• 基本数据类型
  • 整数类型 (integer)、实数类型 (real) 、字符类型 (char)、指针类型 (pointer)
• 复合数据类型
  • 由基本数据类型组合而成的结构
    • 数组 、结构类型等
  • 复合数据类型本身，又可参与定义更为复杂的结点类型

结构(关系)的类型

• 用 R 的性质来刻划数据结构的特点，并进行分类
  • 集合结构（set structure）
  • 线性结构（linear structure）
  • 树型结构（tree structure）
  • 图结构（graph structure）

线性结构

• 又被称为前驱关系
• 关系 r 是有向的
• 满足全序性、单索性
  • 全序性：全部结点两两皆可比较前后
  • 单索性：每个结点都存在唯一一个直接前驱和直接后继结点

树形结构

• 又被称为层次结构
• 每个结点可有多于一个 “直接后继”，但只有唯一的 “直接前驱”
• 最高层结点称为根（root）结点，无父结点

图形结构

• 又被称为网络结构
• 图结构对关系 r 没有施加任何约束
  • 每个结点的直接前驱和直接后继数目没有要求

逻辑结构设计方法

• 自顶向下的设计逻辑
  • 先明确数据结点，及其主要关系 r
  • 在分析关系 r 时，也要分析其数据结点的数据类型
  • 如果数据结点的逻辑结构比较复杂，那么把它作为下一个层次，再分析下一层次的逻辑结构
  • 递归分析，直至满足需求

存储结构

• 亦称物理结构，是逻辑结构在计算机中的物理存储表示
• 计算机主存储器
  • 空间相邻
    • 存储空间是一种具有非负整数地址编码的、空间相邻的单元集合，其基本存储单元是字节
  • 随机访问
    • 计算机指令具有按地址随机访问存储空间内任意单元的能力，访问不同地址所需时间相同
• 存储结构建立一种逻辑结构到物理结构的映射
  • 逻辑结点映射：对于每一个结点 j \(\in\) K 都对应一个唯一的存储区域 c \(\in\) M
  • 逻辑关系映射：每一关系元组 \((j_1,j_2)\in r\)（其中 \(j_1,j_2\in K\) 是结点），亦即 \(j_1,j_2\) 的逻辑关系映射为存储单元的地址顺序关系（或指针地址指向关系）
• 四种基本存储映射方法
  • 顺序、链接、索引、散列

顺序方法

• 顺序存储
  • 结点按地址相邻关系顺序存储，结点间逻辑关系用存储单元的自然顺序关系来表达
  • 数组是顺序存储法的具体实例
• 顺序存储是紧凑存储结构
  • 紧凑：存储空间除存储有用数据外，不存储其他附加信息
  • 存储密度：存储结构所存储 “有用数据” 和该结构（包括附加信息）整个存储空间大小之比
• 一维数组
• 二维数组：支持整数编码访问
  • 行优先存储
  • \(M[i][j]=M[0][0]+i\times \mathrm{sizeof}(M[0])\times \mathrm{sizeof}(M[0][0])\)

链接方法

• 利用存储结构中指针指向来表示两个结点间逻辑关系
• 可以表达任意的逻辑关系 r
• 将数据结点分为两部分：数据字段、指针字段
  • 数据字段：存放结点本身的数据
  • 指针字段：存放指针，链接到某个后继结点，指向存储单元的开始地址
  • 多个相关结点的依次链接就会形成链表
• 优点：增删容易
  • 顺序方法对于经常增、删结点情形，往往遇到困难
  • 链接方法结合动态存储可以解决这些复杂的问题
• 缺点：定位困难
  • 访问结点必须知道该结点的指针
  • 否则需要沿着链接指针逐个搜索，花费时间较大

索引方法

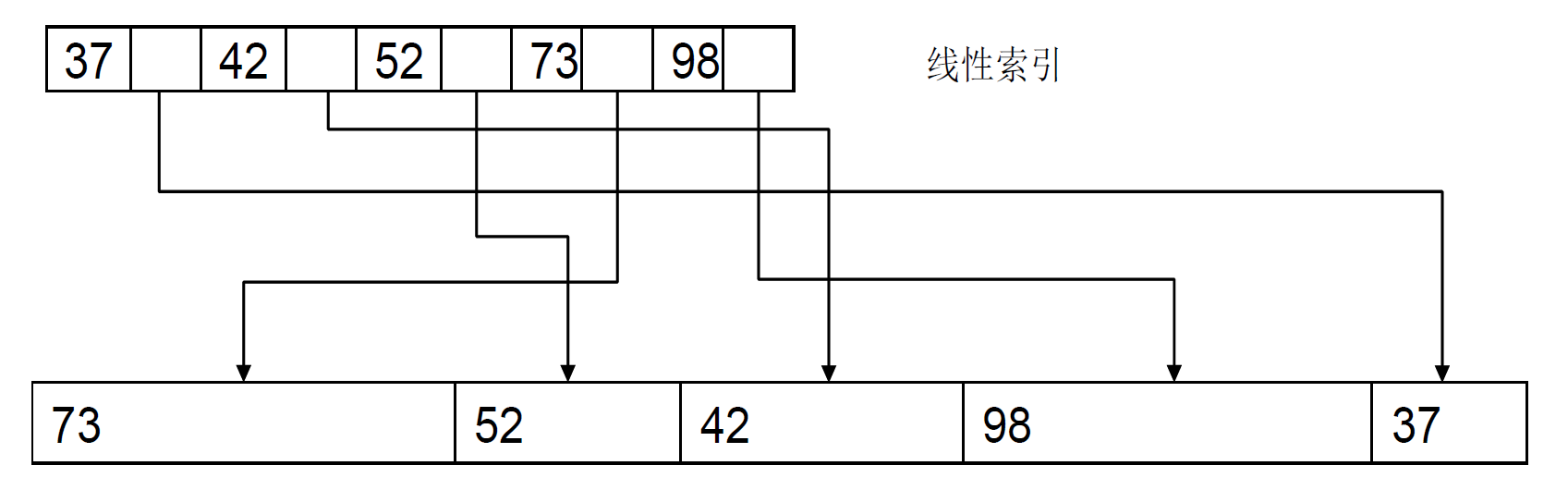
• 是顺序存储法的一种推广
• 索引方法是要建造一个由整数域 Z 映射到存储地址域 D 的函数 Y: Z \(\to\) D，把结点的整数索引值 z \(\in\) Z 映射到结点的存储地址d \(\in\) D
  • Y 称为索引函数

散列方法

• 散列是索引方法的扩展
• 散列函数：将关键码 s 映射到非负整数 z
  • h: s \(\to\) z
• 对任意的 s \(\in\) S，散列函数 h(s)=z，z \(\in\) Z

抽象数据类型 (ADT)

• 抽象问题得到解决，同类具体问题都可得到解决
• ADT 是对多种可能的结构和实现的抽象
• 模块化思想的发展，提供了抽象数据类型的实现手段，简称 ADT (Abstract Data Type)
  • 可以看作是定义了一组操作的一个抽象模型
• 一个抽象数据类型要包括哪些操作，这一点由设计者根据需要确定
• 用数学方法定义对象集合和运算集合，仅通过运算的性质刻画数据对象，而独立于计算机中可能的表示方法
• 目的：隐藏运算实现的细节和内部数据结构
• 三元组：<数据对象，数据关系，数据操作>

ADT 抽象数据类型名 {
    数据对象D: <数据对象的定义>;
    数据关系S: <数据关系的定义>;
    数据操作P: <基本操作的定义>;
} ADT 抽象数据类型名

算法

• 数据结构 + 算法 = 程序设计
• 程序设计的实质：为计算机处理问题编制一组 “指令”
• 需要解决两个问题：算法和数据结构
  • 数据结构 = 问题的数学模型
  • 算法 = 处理问题的策略

算法的性质

• 通用性
  • 对参数化输入进行问题求解 ，保证计算结果的正确性
• 有效性
  • 有限条指令序列能完成算法所要实现的功能
• 确定性
  • 算法描述中的下一步应执行的骤必须明确
• 有穷性
  • 算法的执行必须在有限步内结束
  • 换句话说 ，算法不能有死循环

算法分类

• 穷举法
  • 万能，低效
• 回溯法、搜索 (DFS, BFS)
• 贪心法
  • 最优子结构 —— 最优解
  • 否则 ，只是快速得到次优解
• 递归分治 (二分检索 、快速排序 、分治排序 )
  • 子结构不重复
  • 分、治、合
• 动态规划
  • 自底向上，利用中间结果，迅速构造
  • 最优子结构、重复子结构、无后效性
  • 搜索中分支定界的特例
  • 空间换时间

算法分析

• 算法分析是对一个算法需要多少计算时间和存储空间的定量分析
• 判断所提出的算法是否符合现实情况
• 时间和空间复杂性：trade off

算法复杂性度量

• 不能用绝对时间单位
  • 环境不同
  • 语言不同
  • 可扩展性不同：在不同输入规模上表现不同
• 绝对运行时间的比较也是需要的
• 重要的不是具体的时间，而是算法复杂性与输入数据规模(N)之间的关系
• 用 “输入规模(N)” 所需 “基本操作(B)” 的量级来描述时间复杂性，与操作的具体数值无关

算法的渐进分析

• 大 \(O\) 表示法
  • 如果存在正数 \(c\) 和 \(n_0\)，使得对任意的 \(n>n_0\)，都有 \(f(n)\le cg(n)\)
  • 则称 \(f(n)\) 在集合 \(O(g(n))\) 中，或简称 \(f(n)\) 是 \(O(g(n))\) 的
• \(\Omega\) 表示法
  • 如果存在正数 \(c\) 和 \(n_0\)，使得对任意的 \(n>n_0\)，都有 \(f(n)\ge cg(n)\)
  • 则称 \(f(n)\) 在集合 \(\Omega(g(n))\) 中，或简称 \(f(n)\) 是 \(\Omega(g(n))\) 的
• \(\Theta\) 表示法
  • 如果一个函数既在集合 \(O(g(n))\) 中又在集合 \(\Omega(g(n))\) 中，则称其为 \(\Theta(g(n))\) 的
  • 即存在正数 \(c_1,c_2\) 和 \(n_0\)，使得对任意的 \(n>n_0\)，都有 \(c_1g(n)\le f(n)\le c_2g(n)\)

示例

for (i = 4; i < n; i++) {
    for (j = i-3, sum = a[i-4]; j <= i; j++) {
        sum += a[j];
    }
}

• 外层循环进行 n-4 次
• 对每个 i 而言，内层循环只执行 4 次
  • 每次的操作次数和 i 的大小无关：11 次赋值操作
• 整个代码总共进行1 + 11*(n-4) = O(n)次
• 看似双重循环，其实线性时间

最坏、最好、平均情况

• 算法分析受条件分支的影响
  • 算法的增长率估计往往由于算法中的条件分支而遇到困难
  • 分支走向又受输入数据取值的影响，因此很多算法都无法得出独立于输入数据的渐进估计
• 估计方法
  • 最坏情况估计
  • 最好情况估计
  • 平均情况估计

平均情况

• 简单情况下，需要考虑每种输入情况的概率

\[ \mathrm{C_{avg}=\sum_{i}p(input_i)\times \mathrm{steps}(input_i)} \]

• 对于时间开销，一般不关注算法的最好估计，最坏估计是唯一的选择
  • 特别是处理应急事件，计算机系统必须在规定的响应时间内做完紧急事件处理
• 对于多数算法而言，最坏情况和平均情况估计，它们的时间开销的公式虽然不同，但是往往只是常数因子大小的区别，或者常数项的大小区别。因此不会影响渐进分析的增长率函数估计

时间和空间的折衷

• 空间开销也可以实行类似的渐进分析方法
  • 指除数据本身之外的存储开销
• 静态存储结构
  • 空间开销估计往往容易
• 动态存储结构
  • 算法运行过程中会有数量级地增大或缩小
  • 这种情况的空间开销的分析和估计是十分必要的
• 时空折衷（Trade-off between Time and Space）
  • 空间换时间：为改善算法的时间开销，可通过增大空间开销而设计出时间开销小的算法
  • 时间换空间：为缩小算法的空间开销，通过增大时间开销来换取存储空间的节省