(论文)[1997-SIG] Metropolis Light Transport(1)
Metropolis Light Transport
Abstract
- MLT 是无偏的
- 在复杂场景中表现很好,简单场景中和之前的方法相比也不错
- bright indirect light
- small geometric holes
- glossy surfaces
- MLT 优点,局部搜索
- 平均计算代价小(~1-2 rays)
- 一旦一条重要路径被发现,周围的也会被发现【均摊开销】
- 可以根据光路的相关性设计变异策略
Introduction
- 为了处理真实场景,算法需要足够鲁棒:支持 complex
geometry、materials、illumination
- MCPT 复杂场景失效(例如门缝外的光、焦散等)
- 复杂光路求解:BDPT、Path Guiding(radiance guidance)
- MLT 按照光路对最终图片的贡献去采样
- 第一次将 Metropolis 方法引入 light transport 求解
Overview of the MLT algorithm
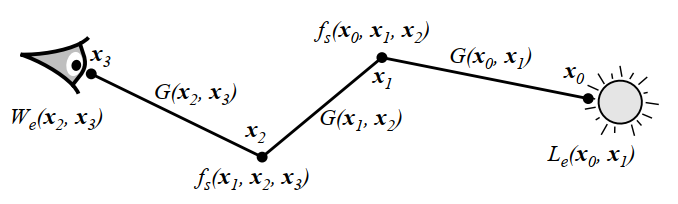
- path \(\bar{x}=\mathrm{x}_0\mathrm{x}_1\cdots\mathrm{x}_k\)
- \(\mathrm{x}_0\) 是光源
- 长度 \(k\ge1\)
- \(f\):image contribution function
\[ \int_{D}f(\bar{x})\;d\mu(\mathrm{x}) \]
- 策略:正比于 \(f\) 对光路进行采样,然后在相机平面记录贡献值
- 生成一系列 paths \(\bar{X}_0,\bar{X}_1,\cdots,\bar{X}_N\)
- \(\bar{X}_i\) 通过 \(\bar{X}_{i-1}\) 随机扰动(random mutation)得到
- mutation 可以随意,典型的包括:添加、删除、替换当前路径的部分节点
- mutation 可以被拒绝,取决于接受率(新老路径的相对贡献)
- 拒绝后 \(\bar{X}_i\) 设置为原来的路径 \(\bar{X}_{i-1}\)
- MLT 框架下,采样的 \(\bar{X}_i\) 最终会服从于 \(f\) 的分布【平稳分布】
- 算法如下

Metropolis sampling algorithm
来源于 computational physics,1953
设定
状态空间 \(\Omega\)
非负函数 \(f:\Omega\to \mathbb{R}^+\)
初始状态 \(\bar{X}_0\in\Omega\)
目标:生成随机游走样本 \(\bar{X}_0,\bar{X}_1,\cdots,\bar{X}_N\),使得不管初始样本是什么,让最终的样本 \(\bar{X}_i\) 的分布正比于 \(f\)
- Metropolis 算法不要求 \(f\) 积分为 1
\(\bar{X}_i\) 通过对 \(\bar{X}_{i−1}\) 的随机扰动生成
- 我们:path mutations
- 马尔科夫链:\(\bar{X}_i\) 只依赖于 \(\bar{X}_{i−1}\)
转移函数 \(K(\bar{y}|\bar{x})\)
\[ \int_{\Omega}K(\bar{y}|\bar{x})\;d\mu(\bar{y})=1,\forall\bar{x}\in\Omega \]
The stationary distribution
- 平稳分布(状态不变)
- \(\bar{X}_i\)都是服从分布 \(p_i\) 的随机变量
\[ p_{i}(\bar{x})=\int_{G}K(\bar{x}|\bar{y})\;p_{i-1}(\bar{y})\;d\mu(\bar{y})\tag{1} \]
- \(p_i\) 最终会收敛到唯一的分布
\(p\),称为平稳分布
- 注意到 \(p\) 不依赖于初始状态 \(\bar{X}_0\)
Detailed balance
- 细致平衡
- 在实际的物理系统中,\(K\) 是由物理约束决定的,给定初始状态便会变化到平稳分布
- Metropolis 算法与之相反,构建 \(K\)
使得平稳分布正比于 \(f\)(越快越好)
- 达到细致平衡
- 给定 \(\bar{X}_{i-1}\),如果过程生成 \(\bar{X}_i\)
- 通过 tentative transition function \(T\) 生成一个样本 \(X_i'\)
- \(T(X_i'|\bar{X}_{i-1})\) 表示转移概率
- 按照接受率 \(a\) 接受
\[ X_i= \left\{ \begin{array}{ll} \bar{X}_i' &\text{with probability }a(\bar{X}_i'|\bar{X}_{i-1})\\ \bar{X}_{i-1} &\text{otherwise} \end{array} \right. \tag{2} \]
- 细致平衡条件【达到平稳分布的充分条件】
\[ f(\bar{x})\;T(\bar{y}|\bar{x})\;a(\bar{y}|\bar{x})=f(\bar{y})\;T(\bar{x}|\bar{y})\;a(\bar{x}|\bar{y})\tag{3} \]
- 细致平衡条件是平稳分布的充分条件
- 假定 \(p_{i-1}\propto f\) 而且满足细致平衡
\[ \begin{aligned} p_{i}(\bar{x})=&\Big[1-\int_{\Omega}T(\bar{y}|\bar{x})\;a(\bar{y}|\bar{x})\;\mathrm{d}\mu(\bar{y})\Big]p_{i-1}(\bar{x})\\ &+\int_{\Omega}p_{i-1}(\bar{y})T(\bar{x}|\bar{y})\;a(\bar{x}|\bar{y})\;\mathrm{d}\mu(\bar{y})\\ &\\ &=p_{i-1}(\bar{x})\\ \end{aligned}\tag{4} \]
The acceptance probability
- 接受概率
- \(f\) 给定,\(T\) 任意选取,等式 (3)取决于 \(a(\bar{y}|\bar{x})/a(\bar{x}|\bar{y})\).
- 为了快速收敛,希望 \(a\) 越大越好
\[ a(\bar{y}|\bar{x})=\min\Big\{1,\dfrac{f(\bar{y})T(\bar{x}|\bar{y})}{f(\bar{x})T(\bar{y}|\bar{x})}\Big\} \]
- 按照这个规则,有一个方向的转移一定会被接受【另一个方向可能被拒绝,但是总的移动步数期望是一样的】
遗传算法对比
- MLT 解决采样问题,遗传算法解决优化问题
- 遗传算法在群体中起效,MLT 只需要保存当前状态
- 遗传算法的变异策略更随意,MLT 有限制(需要算转移概率)
- Rayvolution: An evolutionaryray tracing
algorithm【EGSR Workshop 1994】
- 利用遗传算法优化半球面的积分,优化 incident radiance 的分布【path guiding?没找到论文】
The path integral formulation of light transport
- MLT 基于路径空间的形式
The light transport equation
- 光传输方程
\[ L(\mathrm{x'}\to\mathrm{x''})=L_e(\mathrm{x'}\to\mathrm{x''})+\int_{\mathcal{M}}L(\mathrm{x}\to\mathrm{x'})f_s(\mathrm{x}\to\mathrm{x'}\to\mathrm{x''}){\color{red}G(\mathrm{x}\leftrightarrow\mathrm{x'})}\;\mathrm{d}A(\mathrm{x}) \]
- \(\mathcal{M}\) 表面集合
- \(A\) 面积度量
- \(G\) 几何项与可见性
- \(V\) 可见性
\[ G(\mathrm{x}\leftrightarrow\mathrm{x'})=V(\mathrm{x}\leftrightarrow\mathrm{x'})\dfrac{|\cos\theta_o\cos\theta_i'|}{\Vert\mathrm{x}-\mathrm{x'}\Vert^2} \]
The measurement equation
\[ m_j=\int_{\mathcal{M}\times\mathcal{M}}W_e^{(j)}(\mathrm{x}\to\mathrm{x}')L(\mathrm{x}\to\mathrm{x}')G(\mathrm{x}\leftrightarrow\mathrm{x}')\;\mathrm{d}A(\mathrm{x})\;\mathrm{d}A(\mathrm{x}') \]
- \(m_j\) 表示对最终图片的贡献
- \(W_e^{(j)}(\mathrm{x}\to\mathrm{x'})\)
- 实际:相机响应函数(flux responsivity )
- 渲染:重要性函数(importance function)
The path integral formulation
- 路径积分形式:递归展开
\[ \begin{aligned} m_j=&\int_{\mathcal{M}^2}L(\mathrm{x}_0\to\mathrm{x}_1)G(\mathrm{x}_0\leftrightarrow\mathrm{x}_1)W_e^{(j)}(\mathrm{x}_0\to\mathrm{x}_1)\;\mathrm{d}A(\mathrm{x}_0)\;\mathrm{d}A(\mathrm{x}_1)\\ &+\int_{\mathcal{M}^3}L(\mathrm{x}_0\to\mathrm{x}_1)G(\mathrm{x}_0\leftrightarrow\mathrm{x}_1)f_s(\mathrm{x}_0\leftrightarrow\mathrm{x}_1\leftrightarrow\mathrm{x}_2)G(\mathrm{x}_1\leftrightarrow\mathrm{x}_2)W_e^{(j)}(\mathrm{x}_1\to\mathrm{x}_2)\;\mathrm{d}A(\mathrm{x}_0)\;\mathrm{d}A(\mathrm{x}_1)\;\mathrm{d}A(\mathrm{x}_2)\\ &\cdots\\ \end{aligned} \]
- 能够写成统一的形式
\[ m_j=\int_{\Omega}f_j(\bar{x})\;\mathrm{d}\mu(\bar{x}) \]
- \(\Omega_k\) 长度为 \(k\) 的路径集合
- \(\bar{x}=\mathrm{x}_0\mathrm{x}_1\cdots\mathrm{x}_k\),\(k\ge1\land\forall x_i\in\mathcal{M}\)
\[ \mathrm{d}\mu_k(\mathrm{x}_0\cdots\mathrm{x}_k)=\mathrm{d}A(\mathrm{x}_0)\cdots\;\mathrm{d}A(\mathrm{x}_k) \]
- \(\Omega\) 路径全空间(\(\Omega_k\) 的并), \(\mu\) 表示 \(\Omega\) 上的度量
- \(D\) 表示特定路径,右边表示找到其对应长度所在的子空间,然后度量
\[ \mu(D)=\sum_{k=1}^{\infty}\mu_k(D\;\cap\Omega_k) \]
- \(f_j\):measurement contribution function
- 例子
\[ f_j(\mathrm{x}_0\mathrm{x}_1)=L_e(\mathrm{x}_0\to\mathrm{x}_1)G(\mathrm{x}_0\leftrightarrow\mathrm{x}_1)W_e^{(j)}(\mathrm{x}_0\to\mathrm{x}_1) \]
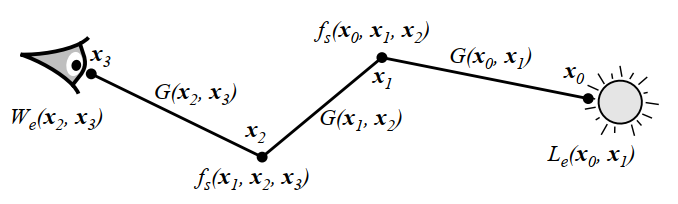
- 上面转化的目的:表示成统一的积分形式,方便 MLT