阴影算法的实现(SM、PCF、PCSS、VSM)

阴影算法的实现

• 我们实现了从最经典的 Shadow Map 算法开始，实现了一系列的软阴影算法，包括 PCF、PCSS、VSM 三种软阴影算法
• 如下是我们的算法实现过程以及结果展示

说明

• 环境
  • VS2017 x86
  • OpenGL 4.6（版本设置成了 3.3，之后的都行）
• 依赖库
  • glad 0.1.34
  • glfw 3.3
  • glm 0.9.9.8
• 代码
  • Github，需要按照 README 配置
  • 打包好的源代码
  • PPT 报告

算法介绍

SM

• Shadow Mapping
• 传统的 two-pass 阴影算法
  • 第一个 pass，切换到以光源为视点的观察坐标系中，利用帧缓冲生成一张深度图 DepthMap
  • 第二个 pass，正常渲染，对渲染的每一个 fragment 做可见性判断，得到一个非零即一的 visibility
    • 将 shading point 通过第一个 pass 的变换得到的深度值和 DepthMap 中记录的对应位置的深度值作比较
    • 如果 DepthMap 中记录的值小，说明当前的点对光源不可见，visibility=0
    • 否则 visibility=1
    • 用 visibility 乘上当前点的直接光照，进行遮蔽效果
• 在实现上可以使用定向光做平行投影生成 DepthMap，也可以使用点光源做透视投影生成 DepthMap

PCF

• Percentage Closer Filter
• 由于 SM 得到的阴影结果是非零即一的值，这样子我们得到的边界就是一个很生硬的过渡（硬阴影），而实际生活中我们看到的阴影是有一个比较平滑的过渡（软阴影），这是由于我们定向光和点光源的假设在生活中是不成立的。生活中的光源是占据一块区域的，而不是只有一个点
• 为了模拟这种软阴影的效果，我们在 SM 第二个 pass 的时候做如下处理
  • 对于每一个 shading point，我们将其变换到以光源为视点的观察坐标系中的深度值和它对应的周围的 N 个点进行深度比较，求出一个 visibility 值
  • \(\mathrm{visibility}=\dfrac{深度比当前点深度值大的采样点数目}{\mathrm{N}}\)
  • 这样子我们得到的 visibility 的值就不是简单的非零即一的值，于是在边界产生过渡的效果
• 上面的周围我们一般是给定半径 R，在半径为 R 的圆形区域内采样

PCSS

• Percentage Closer Soft Shadow
• 我们在生活中还观察到另外一种现象，物体越靠近投射出阴影的平面，阴影越偏向于硬边界，物体越远离投射出阴影的平面的时候，阴影越偏向于软边界
• 如下图中，笔尖部分的阴影更硬，远离笔尖部分的阴影更软

• 这原因很简单，物体离成阴影平面越近，阴影过渡区域（半影）越小
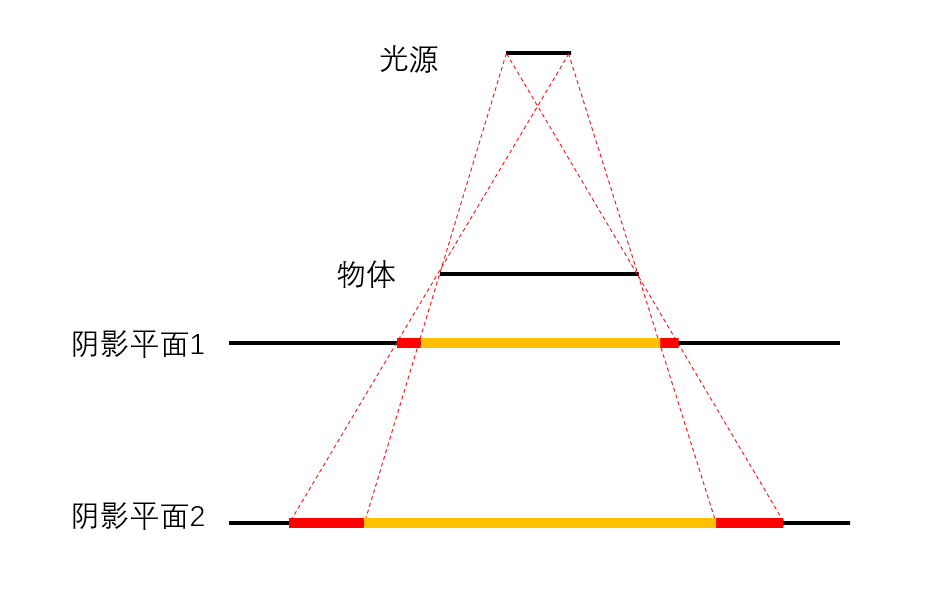
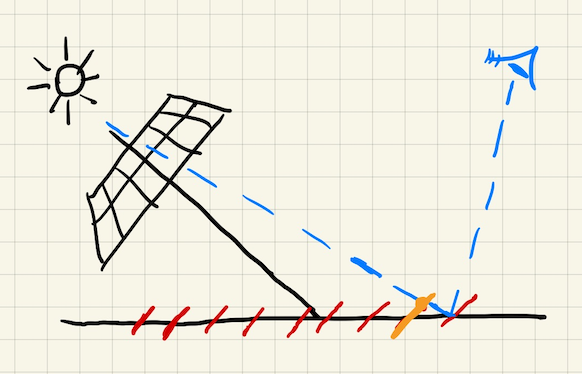
• 下图中
  • 红色区域表示半影区域
  • 黄色部分表示全影区域
  • 显然在阴影平面 1 上半影区域比阴影平面 2 更小

• 我们加一条蓝色的辅助线，我们发现阴影平面1上半影区域占全影区域的比例也更小

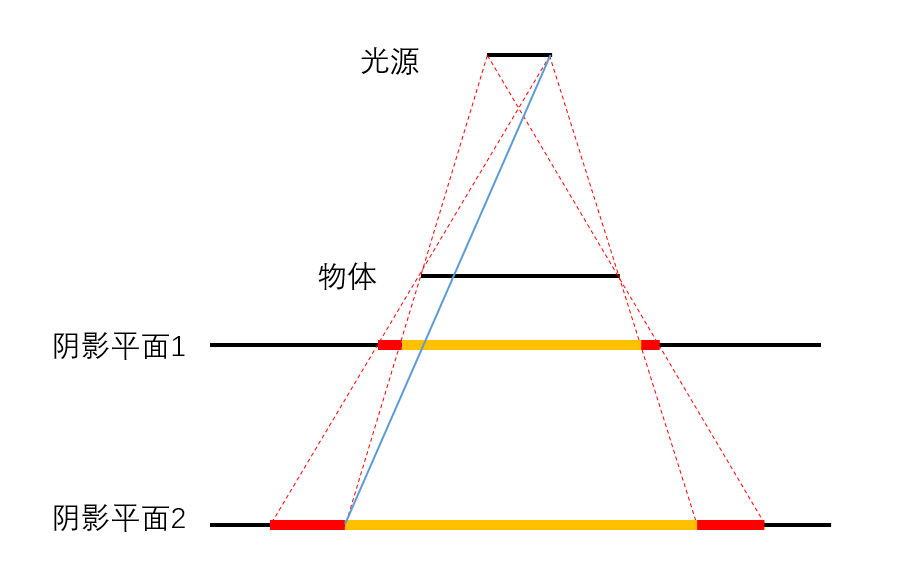
• 也就是说我们要通过物体到阴影平面的距离来决定阴影的软硬程度，也就是采样半径 R 的大小
• 我们从上图中也了解到，半影区域也就是阴影过渡的区域，因此我们可以通过半影的大小估计采样半径 R
• 估计方式如下图所示

\[ w_{penumbra}=\dfrac{d_{Receiver}-d_{Blocker}}{d_{Blocker}}\cdot w_{Light} \]

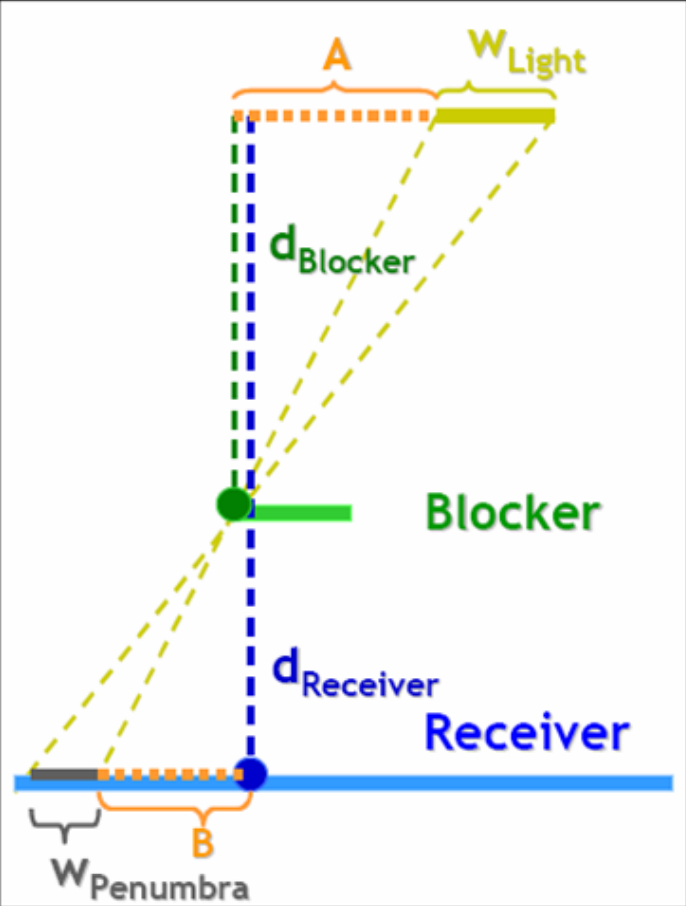
• 但是同时这里出现了另外一个问题，\(d_{Blocker}\) 的计算问题，可以通过给定固定范围的计算得到，或者启发式的计算得到

VSM

• Variance Shadow Mapping
• VSM 算法试图使用计算的方式避免采样，因为采样是一个很慢的过程
• 我们对 shading point 周围的点进行深度的采样，计算得到的 visibility 本质上就是在估计周围有百分之多少的点深度值比当前点大，也就是说如果我们能够获取到这个百分比，就不需要采样了
• 切比雪夫不等式可以实现这一点

\[ P(x>t)\le\dfrac{\sigma^2}{\sigma^2+(t-\mu)^2} \]

• 切比雪夫不等式的条件是 \(t>\mu\) 以及分布是一个单峰的分布
• 给定一个深度值 t，我们可以通过其周围的深度均值与方差估计出当前点深度的排名
• 当然实时渲染中我们不等式直接当等式使用

场景说明

• 我们的场景比较简单
  • 一个点光源
  • 一个跳动的小球和一排方柱子

算法实现

着色模型

• 使用 Blinn-Phong 着色模型，由 diffuse + specular + ambient 三部分组成
• shader 主要代码如下

void main() {
    // 环境光 ambient
    vec3 ambient = 0.2 * color;

    // 漫发射光 diffuse
    vec3 lightDir = normalize(lightPos - fs_in.FragPos);
    vec3 normal = normalize(fs_in.Normal);
    float diff = max(dot(lightDir, normal), 0.0);
    vec3 diffuse = diff * color;

    // 镜面高光 specular
    vec3 viewDir = normalize(viewPos - fs_in.FragPos);
    vec3 reflectDir = reflect(-lightDir, normal);
    float spec = 0.0;

    // Blinn-Phong 模型考虑法线和半角矢量的夹角
    vec3 halfwayDir = normalize(lightDir + viewDir);
    spec = pow(max(dot(normal, halfwayDir), 0.0), 32.0);
    vec3 specular = vec3(0.3) * spec;

    float visibility = 1.0f;

    // 阴影算法
    // ...

    FragColor = vec4(
        ambient + visibility*(diffuse + specular), 
        1.0);
}

• 没有阴影的效果如下，缺乏真实感

SM

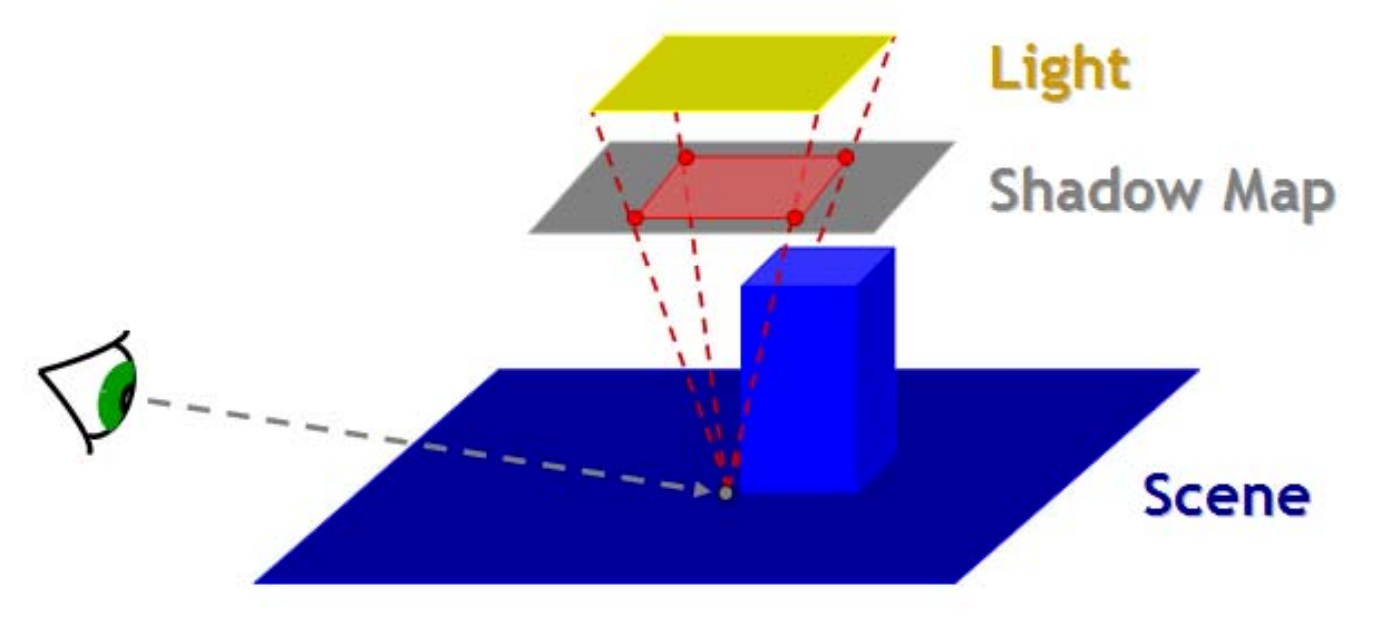
• 第一趟利用 OpenGL 的帧缓冲生成一张 DepthMap
• 第二趟比较即可
• shader 代码如下
  • 注意这里的 DepthMap 中虽然你保存的是透视投影的深度，但是我们不需要变换成线性深度，因为只需要知道相对大小即可

// 处于阴影之中: 0.0
// 否则返回 1.0
float ShadowCalculation(vec4 fragPosLightSpace) {
    // 转化为标准齐次坐标, z:[-1, 1]
    vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
    // xyz:[-1, 1] => [0,1]
    projCoords = projCoords * 0.5 + 0.5;
    // 在深度图中获取深度信息
    float closestDepth = texture(depthMap, projCoords.xy).r;
    // 当前片元的深度
    float currentDepth = projCoords.z;
    // 判断是否处于阴影当中
    float shadow = currentDepth-BIAS > closestDepth  ? 1.0 : 0.0;
    return 1.0 - shadow;
}

void main() {
    // ...
    visibility = ShadowCalculation(fs_in.FragPosLightSpace);
    // ...
}

• 效果如下，是我们想象中的硬阴影

• 注意上面的 BIAS 是为了解决自遮挡现象（黑白条纹）
  • 由于 Z-Buffer 分辨率有限导致的
  • 下图形象说明了这点，蓝色的点竟然不可见了

• 不加 BIAS 的效果

PCF

• PCF 的实现和 SM 类似，只需要对周围点多采样几个即可，我们直接对周围 R \(\times\) R 的点进行一个遍历

// PCF 算法
float PCF(vec4 fragPosLightSpace, float radius) {
    // 采样距离修正
    radius *= PCF_SampleRadius;

    vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
    projCoords = projCoords * 0.5 + 0.5;
    float shadow = 0.0;
    float currentDepth = projCoords.z;
    vec2 texelSize = 1.0 / textureSize(depthMap, 0); // 0 级纹理相邻纹素的距离
    for(int x = -PCF_RADIUS; x <= PCF_RADIUS; ++x) {
        for(int y = -PCF_RADIUS; y <= PCF_RADIUS; ++y) {
            float shadowMapDepth = texture(depthMap, projCoords.xy + radius*vec2(x, y) * texelSize).r;
            shadow += currentDepth-BIAS > shadowMapDepth  ? 1.0 : 0.0;
        }
    }
    float total = (2*PCF_RADIUS+1);
    return 1.0 - shadow/(total*total);
}

void main() {
    // ...
    visibility = PCF(fs_in.FragPosLightSpace, 1.0);
    // ...
}

• PCF_SampleRadius 修正是服务于 PCSS 的，试图让阴影扩散
  • 因为我们不想让采样数过多，但是又需要考虑一个相对比较大的半径时，增大采样间隔
• 效果如下，阴影变成了软阴影，但是所有阴影的边界模糊程度是相似的

PCSS

• PCSS 分为 3 个步骤
  • Step 1: Blocker search
    • 在某个区域内计算平均遮挡深度
  • Step 2: Penumbra estimation
    • 通过计算出来的平均遮挡深度来计算半影的大小
  • Step 3: Percentage Closer Filtering
    • 根据 Step 2 计算出来的大小进行 PCF
• 主体思路如下，由于我们需要进行深度的平均计算，这里必须使用线性深度

float PCSS(vec4 fragPosLightSpace){

    // depthMap 中的坐标
    // => [-1, 1]
    vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
    // 转换为线性深度
    float depth = getLinearizeDepth(projCoords.z);
    // [-1, 1] => [0, 1]
    projCoords = projCoords * 0.5 + 0.5;
    // STEP 1: avgblocker depth
    float avgDepth = findBlocker(projCoords.xy, depth);
    // 没有遮挡物
    if(avgDepth == -1.0) {
        return 1.0;
    }

    // STEP 2: penumbra size
    float penumbra = (depth - avgDepth) / avgDepth * lightWidth;
    float filterRadius = penumbra * NEAR_PLANE / (depth);

    // STEP 3: filtering
    return PCF(fs_in.FragPosLightSpace, filterRadius);
}

void main() {
    // ...
    visibility = PCSS(fs_in.FragPosLightSpace);
    // ...
}

• 第一步我们根据上面提到的启发式估计方法计算得到
  • 这里的弥散参数修正是用于控制软阴影的边界，如果小了会被原来硬阴影的边界限制住（外面的都是可见）

/**
* uv: depthMap 中的坐标
* zRecerver: 计算得到的线性深度值 [0, 1]
*/
float findBlocker(vec2 uv, float zReceiver) {
    int blockers = 0;
    float ret = 0.0;
    float r = lightWidth * (zReceiver - NEAR_PLANE/FAR_PLANE) / zReceiver;
    // 弥散参数修正
    r *= SMDiffuse;
    vec2 texelSize = 1.0 / textureSize(depthMap, 0); // 0 级纹理相邻纹素的距离
    for(int x = -BLOCK_RADIUS; x <= BLOCK_RADIUS; ++x) {
        for(int y = -BLOCK_RADIUS; y <= BLOCK_RADIUS; ++y) {
            // [0, 1]
            float shadowMapDepth = texture(depthMap, uv + r*vec2(x, y) * texelSize).r;
            // [0, 1] => [-1, 1]
            shadowMapDepth = getLinearizeDepth(shadowMapDepth * 2.0 - 1.0);
            if(zReceiver - BIAS > shadowMapDepth) {
                ret += shadowMapDepth;
                ++blockers;
            }
        }
    }
    // 没有 blocker
    if(blockers == 0) {
        return -1.0;
    }
    return ret/blockers;
}

• 当第一步找到的平均遮挡物深度为 0 的时候，我们认为当前点可见，返回 visibility=1
• 第二步根据上面的相似三角形计算出 PCF 的采样半径即可
• 第三步就是 PCF
• 效果如下，明显看到软阴影和硬阴影的结果都有

VSM

• 我们需要生成两张图记录当前点对应点周围区域内的方差和均值
• 我们知道 \(\mathrm{var=E(X^2)-E^2X}\)，因此我们只需要记录两张图，分别记录当前点周围区域的 \(\mathrm{EX,EX^2}\) 即可
• 第一个 pass 我们使用帧缓冲生成一张颜色缓冲，R 通道记录深度值 \(\mathrm{d}\)，G 通道记录 \(\mathrm{d^2}\)
• 然后我们需要生成一张周围点的均值和方差
  • 利用两趟 pass 对周围的周围的点求平均值实现
  • 两趟 pass 可以把每一个点的复杂度从 \((2R+1)^2\) 降到 \((4R+2)\)

#define R 5
#define R21 11

void main() {
    vec2 d = vec2(0, 0);
    vec2 texelSize = 1.0 / textureSize(d_d2, 0);
    if(vertical) {
        float r = texelSize.y;
        for(int i = -R; i <= R; ++i) {
            d += texture(d_d2, vec2(TexCoords.x, TexCoords.y + i*r)).rg;
        }
    } else {
        float r = texelSize.x;
        for(int i = -R; i <= R; ++i) {
            d += texture(d_d2, vec2(TexCoords.x + i*r, TexCoords.y)).rg;
        }
    }
    FragColor.rg = d/R21;
}

• 最后一个 pass 的可见性估计如下
  • 注意这里如果不满足切比雪夫不等式的条件的话，直接返回可见即可（深度值比平均深度小）

// VSM 算法
float VSM(vec4 fragPosLightSpace) {
    vec3 projCoords = fragPosLightSpace.xyz / fragPosLightSpace.w;
    // 转换为线性深度
    float depth = getLinearizeDepth(projCoords.z);
    // [-1, 1] => [0, 1]
    projCoords = projCoords * 0.5 + 0.5;

    vec2 d_d2 = texture(d_d2_filter, projCoords.xy).rg;
    float var = d_d2.y - d_d2.x * d_d2.x; // E(X-EX)^2 = EX^2-E^2X

    // 不满足不等式, 直接可见
    if(depth - BIAS < d_d2.x){
        return 1.0;
    }
    else{
        float t_minus_mu = depth - d_d2.x;
        return var/(var + t_minus_mu*t_minus_mu);
    }
}


void main() {
    // ...
    visibility = VSM(fs_in.FragPosLightSpace);
    // ...
}

• 效果如下，很好的软硬阴影结果，和 PCSS 的区别是，柱子的底部阴影更小了

• VSM 存在一个很大的问题，漏光，当不满足单峰的长尾分布时，估计不准确
  • 球的阴影漏光了

其他

• 小球运动的实现
  • 利用物理公式计算出来位置即可
• 小球的实现，类似于经纬度，切分成三角形
  • 注意外面看进去得都是逆时针（OpenGL 逆时针为正向面）

文件说明

• include 文件夹
  • 一些依赖头文件
  • myUtils/basicModel.h：渲染一些基本模型
• lib 文件夹
  • 库文件
• shaders 文件夹
  • gen_SM.vert, genSM_perspective.frag：pass 1 生成 DepthMap（\(d, d^2\)）
  • light.vert, light.frag：pass 2 渲染光源
  • BlinnPhong.vert, BlinnPhong_perspective.frag：pass 2 渲染场景
  • gen_d_d2.vert, gen_d_d2.frag：生成均值（\(d, d^2\)）
• Demo.exe
  • 可执行文件

执行文件

Demo.exe

• 功能如下
  • W/A/S/D 和鼠标：切换视角
  • 空格：可以让小球开始/停止运动
  • P/L： 增大/减小光源宽度（影响PCSS）
  • O/K：增大/减小平均深度的寻找半径，限制 PCSS 的阴影范围
  • I/J：增大/减小 PCF 采样半径，阴影弥散参数（影响 PCF、PCSS）
  • 0/1/2/3/4：选择阴影种类
    • 0(No Shadow), 1(Shadow Map), 2(PCF), 3(PCSS), 4(VSM)

参考资料

• LearnOpenGL 框架性代码
• GAMES202 课程：PCSS、PCSS/VSM
• Nvidia VSM 白皮书
• PCSS 的平行投影实现
• 论文：Variance Shadow Maps