GAMES202.闫令琪.13.实时光线追踪(2)

Posted on Edited on In Views:
实时光线追踪、空间上的滤波、大滤波核的实现（拆分、逐步增大滤波核）、outlier removal、工业界的降噪方法（SVGF、RAE）
  • https://www.bilibili.com/video/BV1YK4y1T7yY

实时光线追踪

  • 空间滤波
    • 联合双边滤波
    • 大 filter 的实现
    • outlier removal（离群值去除）
  • RTRT 中的技术
    • SVGF：Spatiotemporal Variance-Guided Filtering
    • RAE：Recurrent AutoEncoder

空间滤波

实现目标

  • 实现的效果：降噪
    • 下图是椒盐噪声利用中值滤波实现的效果

  • 这里我们想做的是低通滤波（low-pass）
    • 去除高频噪声
      • 高频中也有信号，同时会造成高频信号的丢失
      • 还存在一些低频的噪声
    • 我们在空间域上进行

输入

  • 一张带有噪声的图片 \(\tilde{C}\)
  • 以可滤波核 \(K\)
    • 可以每个像素有不一样的滤波核

高斯滤波

  • 高斯滤波核
    • 周围值得贡献通过离中心点得距离决定
    • 由高斯函数决定

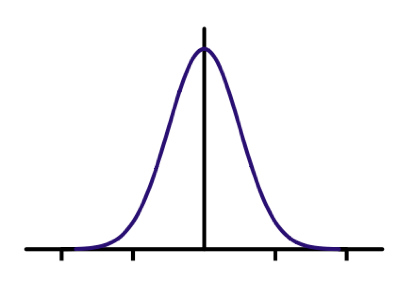
  • 简单的伪代码实现
    • 注意高斯核 \(K\) 的归一化（所有权值和为 1）
      • 伪代码中的 sum_of_weights
      • 同样的我们之前学到的积分拆解，分母中有一个空积分，这也是为了归一化
    • 高斯核本身是无限大的，但是我们可以只考虑比较大贡献的值，例如 \(3\sigma\) 截断
    • 在有些算法实现的时候，会先判断一下 sum_of_weights 是否为 0（高斯这里不可能为 0，就不判断了）
    • 颜色可以是多通道的，此时 sum_of_weights、sum_of_weighted_values 都是多通道的
1
2
3
4
5
6
7
8
For each pixel i:
    sum_of_weights = sum_of_weighted_values = 0.0
    # include i
    For each pixel j around i:
        Calculate the weight w_ij = G(|i - j|, sigma)
        sum_of_weighted_values += w_ij * C^{input}[j]
        sum_of_weights += w_ij
        C^{output}[I] = sum_of_weighted_values / sum_of_weights

双边滤波

  • Bilateral Filtering
  • 高斯滤波的问题
    • 图像一些高频细节也同时缺失了，例如边界也被模糊了
    • 但是我们想要保留边界的信息
  • 下图是一个例子

  • 双边滤波的目的就是在去噪的同时能够保持边界
  • 基于我们生活中的观察
    • 边界：颜色变化非常剧烈
  • idea：如何保持边界
    • 循环的时候我们看 j 点和 i 点的颜色是不是相差特别大
      • 如果相差不是特别大，我们使用原来高斯滤波的方式进行
      • 如果相差特别大，我们就减小贡献值（减小权值）
  • 一种实现如下
    • 两个点 \((i,j),(k,l)\)
    • 值差别过大的时候，那么贡献就会减小

\[ w(i,j,k,l)=\exp\left(-\dfrac{(i-k)^2+(j-l)^2}{2\sigma_d^2}-\dfrac{\Vert I(i,j)-I(k,l)\Vert^2}{2\sigma_r^2}\right) \]

  • 效果如下
    • 能够很好的保留边界信息
    • 山内部的高频信息被抹掉了，但是边界信息保留了

  • 问题
    • 噪声很明显的图会出问题
    • 分不清噪声和边界

联合双边滤波

  • Cross/Joint Bilateral Filtering
  • 观察
    • 高斯滤波：position distance
    • 双边滤波：position distance + color distance
  • 于是我们可以用更多的标准，让结果更加接近我们想要的值
  • 这就是联合双边滤波
  • 联合双边滤波对蒙特卡洛路径追踪算法得到图片的降噪效果很好
    • Especially good at denoising path traced rendering results!
  • 使用哪些信息呢？
    • G-Buffer
      • 世界坐标
      • 法向
      • albedo
      • object ID（每种物体标一个数字）：motion vector 中使用过
    • G-Buffer 本身是完全没有噪声的
      • 和多次反射无关
  • 和之前的滤波一样，不需要考虑归一化
    • 在实现的时候对滤波核进行归一化即可，函数不需要归一化
  • 也可以使用其他函数，不一定是高斯函数，只要随着距离有衰减就可以
  • 高斯函数、指数函数、余弦函数

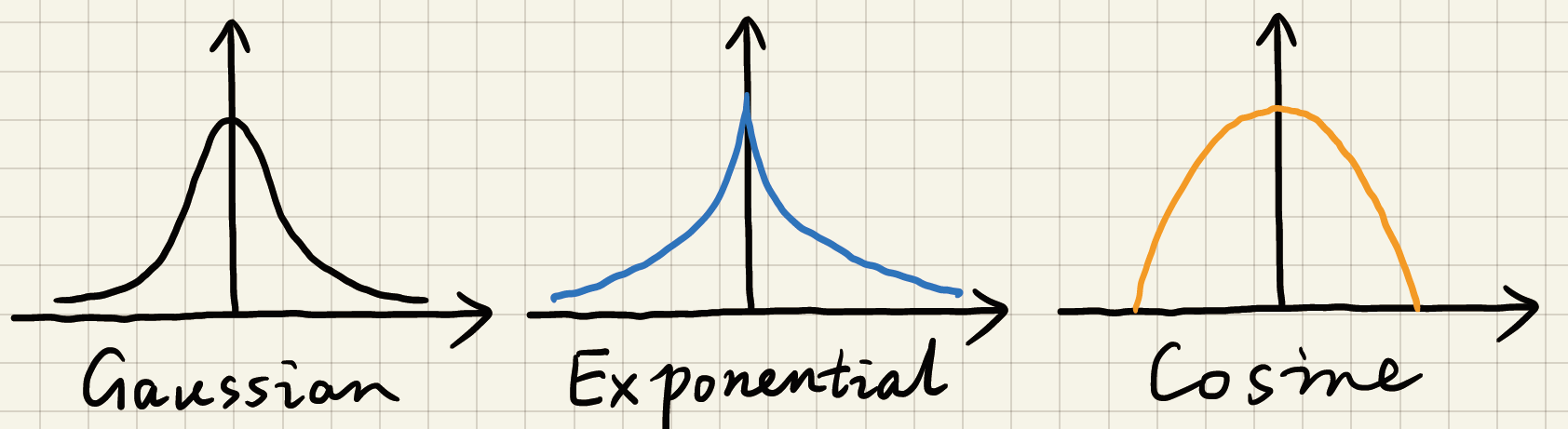
  • 高斯也不需要是严格的高斯，系数什么的都可以变

联合双边滤波例子

  • 我们渲染得到了如下图片，同时得到了 G-Buffer 如下
    • Depth
    • Normal
    • Color

  • 如果我们需要保留边界，则可以使用如下信息作为标准（metric）
  • A-B：position + depth
  • B-C：position + normal
  • D-E：position + color
    • 有噪声的情况下可能会有些问题，color 可能是噪声
  • 具体哪一个标准占的权重大小由 \(\sigma\) 调节
    • 比如上面双边滤波中的 \(\sigma_d,\sigma_r\)

实现大的滤波核

  • Implementing Large Filters
  • 我们在滤波的时候，如果滤波核特别大，计算开销就很大

大滤波核的解决思路

  • FFT（快速傅里叶变化）在 GPU 上的优化做的并不好，因此还是基于空间域上的实现

(1) 拆分：Separate Passes

  • 例如对一个高斯滤波，我们可以先水平方向做一次，然后在竖直方向做一次

  • 对每一个像素，对周围点的查询次数由 \(N^2\) 变成了 \(2N\)
    • \(N\) 为滤波核的大小
高斯函数拆分的数学原理
  • 高斯滤波为什么能这么拆？数学原理如下
  • 高斯函数有好的定义

\[ G_{2D}(x,y)=\exp\left(-\dfrac{x^2+y^2}{2\sigma^2}\right) \]

\[ G_{1D}(x)=\exp\left(-\dfrac{x^2}{2\sigma^2}\right) \]

\[ G_{1D}(y)=\exp\left(-\dfrac{y^2}{2\sigma^2}\right) \]

\[ G_{2D}(x,y)=G_{1D}(x)\cdot G_{1D}(y) \]

  • 滤波就是卷积（filtering == convolution）

\[ \begin{aligned} R(x_0,y_0)&=\iint{F(x_0,y_0)G_{2D}(x_0-x,y_0-y)}\;\mathrm{d}x\mathrm{d}y\\ &=\iint{F(x_0,y_0)G_{1D}(x_0-x)G_{1D}(y_0-y)}\;\mathrm{d}x\mathrm{d}y\\ &=\int\Big(F(x_0,y_0)G_{1D}(x_0-x)\;\mathrm{d}x\Big)G_{1D}(y_0-y)\mathrm{d}y \end{aligned} \]

  • 双边高斯滤波就不能这么拆分，因为不具备定义上 2D 拆分为 1D 的性质
    • 但是在实际工业实现上，都是这么强行拆分的

(2) 逐步增大滤波核：Progressively Growing Sizes

  • 一个例子：a-trous wavelet
  • 每一趟都是 \(5\times5\) 的大小，但是每一趟像素间的间隔是不一样的
  • 第 \(i\) 趟考虑的点间隔 \(2^{i}\)
    • 第 \(1\) 趟（\(i=0\)）
    • 考虑的点示例如下

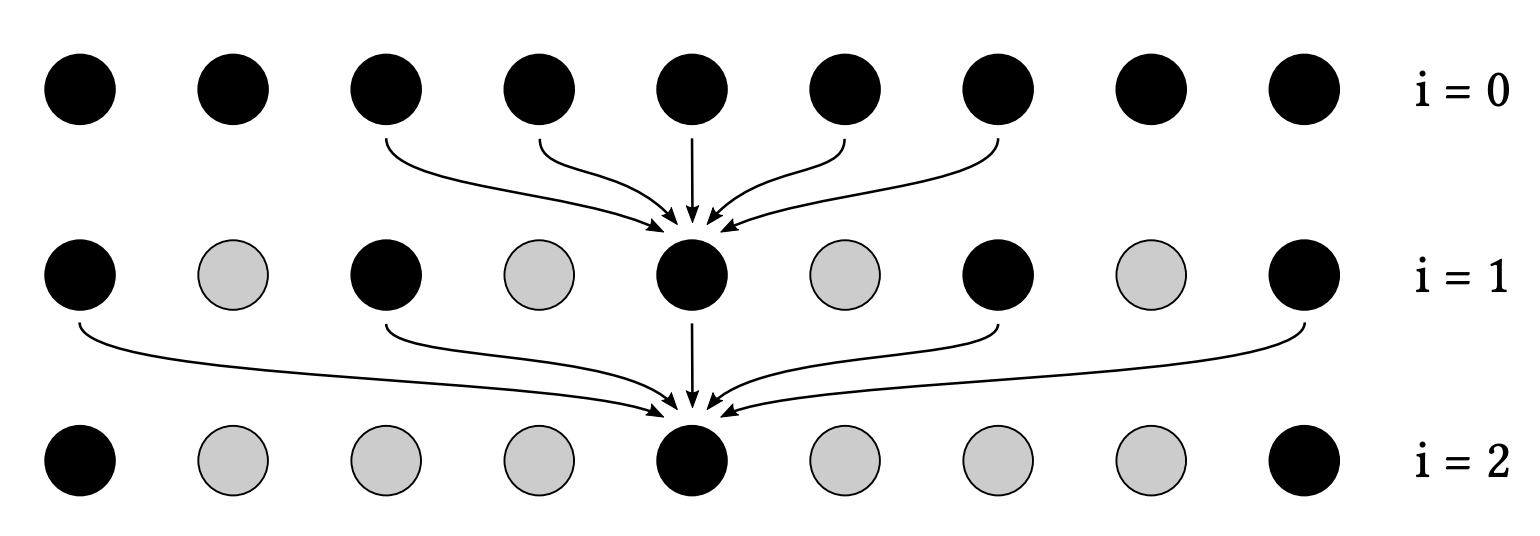
  • 因此我们对于原始 \(64\times64\) 的滤波，对于每一个像素点访问周围点的次数从 \(64\times64\) 降到了 \(5^2\times5\)
    • 第 \(5(i=4)\) 层的时候，间隔为 \(2^4=16\)，一共 \(5\) 个点，\(4\) 个间隔，结果占据范围为 \(64\)
    • \(4096\Rightarrow125\)
原理
  • 为什么要一开始不直接使用大的 filter？
    • 使用更大的 filter == 消除更低的频率
  • 跳过一些采样点为什么是可行的？
    • 更低的频率间隔更大
    • 空间采样，频域上频谱的搬移
      • 如果采样频率太低（间隔太大），会导致走样
      • 采样定理
    • 因为频率变低了，因此可以跳过一些采样点

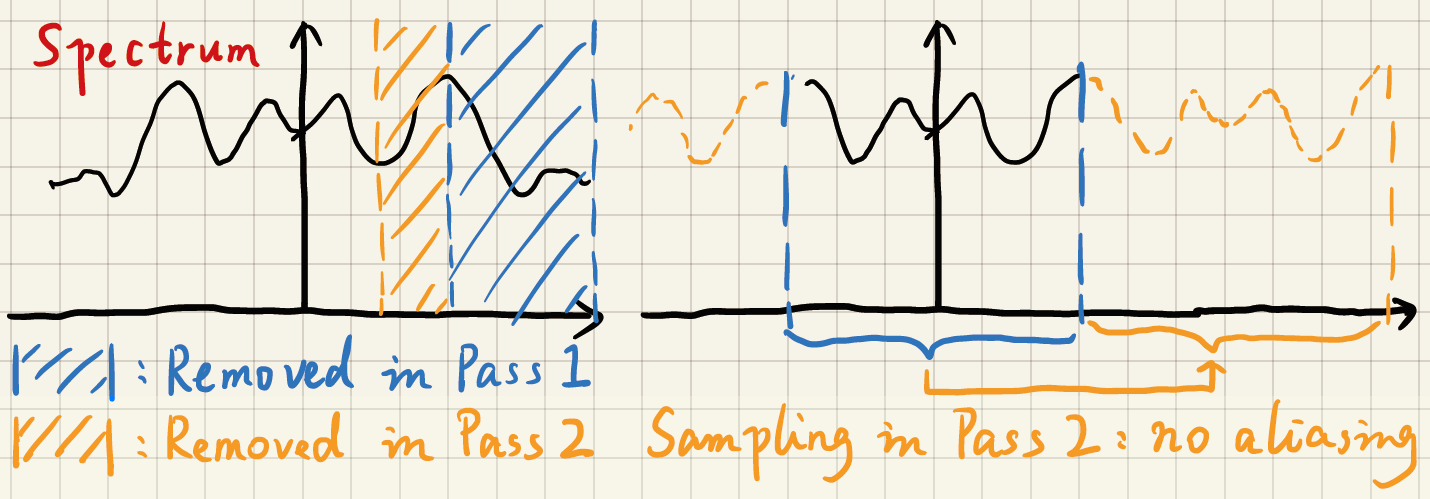
  • 根据上图
    • 第一个 pass，把蓝色部分的高频信息去掉了
    • 第二个 pass 间隔较大，可以去掉黄色部分的高频信息
      • 同时不会有走样现象，因为高频信息已经被去掉了
      • 可以通过计算得到，频谱搬移的时候恰好不会有混叠
  • 在实际中是有问题的，高频信息并不是完全被去掉（非理想滤波器）
    • 能看到一些格子状的 artifact

Outlier Removal

  • Outlier Removal (and temporal clamping)
  • 离群值去除
  • 我们在渲染的过程中可能会出现一些特别亮的点，如下图

  • 这些点在滤波中很难处理，这个点很亮（值很大），在滤波之后会被扩散为一个光晕（比较大的亮斑）
    • the filtered results are still noisy, even blocky
    • blocky artifact
  • 这些特别亮的点就被称为是 outlier
    • 图形学中常被称为是 firefly（火萤）
  • outlier removal 会导致能量不守恒
    • RTRT 为了提高效率，这么做是可以接受的

过程

  • 在做滤波之前先处理掉（不处理掉会影响滤波）
  • outlier 检测
    • 对于每个像素，查看周围的一个小邻域（\(7\times7\)）
    • 计算邻域内的均值、方差（也可以用中位数）
      • 简单计算
      • 用一些数据结构
    • 如果一个点的值在均值加减若干个标准差范围内，如果超出这个范围，我们认为他们就是 outlier
      • \([\mu-k\sigma,\mu+k\sigma]\)
      • 工业界 \(k=1\sim3\) 都有
  • outlier removal
    • 将 outlier 截断（clamp）
    • 工业界 clamp 的实现比较复杂，可能不是一个简单的区间

TAA 中的 outlier removal

  • \(\bar{C}^{(i)}=\alpha\bar{C}^{(i)}+(1-\alpha)\bar{C}^{i-1}\)
  • 我们对上一帧得到的 noise free 的结果进行截断
    • 如果上一帧的结果和这一帧相差太大，我们做一个截断的操作
    • 这样的操作是一个 noise 和 lagging 的 tradeoff
      • 引入了更多噪声
    • 相当于调整 \(\alpha\)
  • \(\bar{C}^{(i)}=\alpha\bar{C}^{(i)}+(1-\alpha)\cdot\mathrm{clamp}(\bar{C}^{i-1},\mu-k\sigma,k+k\sigma)\)

SVGF

3 个标准

depth

  • 深度
  • \(q\) 对 \(p\) 的贡献

\[ w_z=\exp\Big(-\dfrac{|z(p)-z(q)|}{\sigma_z|\nabla z_p\cdot(p-q)|+\epsilon}\Big) \]

  • 不是高斯，分子是一次方（有衰减即可）
  • 分母的 \(\epsilon=10^{-6}\) 防止除零的发生（\(p=q\)）
  • \(\nabla z\) is the gradient of clip-space depth with respect to screenspace coordinates

  • 图上的 A、B 两点在同一个平面上，直观上感觉应该 A 对 B 的贡献不小
    • 但是由于这个平面是侧向我们的，深度上有差异，简单的使用深度值的话，计算得到的贡献偏小
    • 我们使用深度在法线上差异作为一个标准（切平面上的深度差异）
    • 分母计算出来的结果就是按照 \(p\) 点的变化率，深度应该变化的值
      • 如果共平面，值和分子相同，计算得到的结果使得贡献值变大

normal

  • 法线

\[ w_n=\max\Big(0,n(p)\cdot n(q)\Big)^{\sigma_n} \]

  • 指数控制衰减的快慢（之前的 Blinn-Phong 模型的镜面叶）

  • 如果场景应用了法线贴图，我们使用的是没有法线贴图之前的法线（marco normals）
    • 法线贴图干扰很大

luminance

  • luminance（灰度的颜色值）
  • 如果两个点的灰度值相差过大，则贡献值要减小
    • 例如：A 不应该贡献到 B，B 不应该贡献到 C
  • 但是由于噪声的存在，会让我们的判断有些干扰
  • 我们通过方差来判断噪声
    • 如果方差较大（噪声严重），则不应该过多的相信这两个点之间的差异

  • 表达式如下

\[ w_l=\exp\Big(-\dfrac{|l_i(p)-l_i(q)|}{\sigma_l\sqrt{g_{3\times3}\Big(\mathrm{Var}\big(l_i(p)\big)\Big)}+\epsilon}\Big) \]

  • 方差具体计算
    • spatial：我们对当前帧待判断像素点周围 \(7\times7\) 区域方差值（实际上的标准差）
    • temporal：通过 motion vector 找到上一帧中的对应点，求一个方差的平均（带权）
    • spatial：在使用的时候，我们在周围取一个 \(3\times3\) 区域内求一个平均值

评价

  • 方差项会导致在做 over blur 和 noise 之间的 trade off 的时候，会倾向于 over blur
  • 改进：ASVGF
    • 更加精准的判断 temporal上的连续情况
    • overblur 的不要这么厉害（相对噪声会严重些）
  • motion vector 同样会导致拖尾的结果

RAE

网络结构

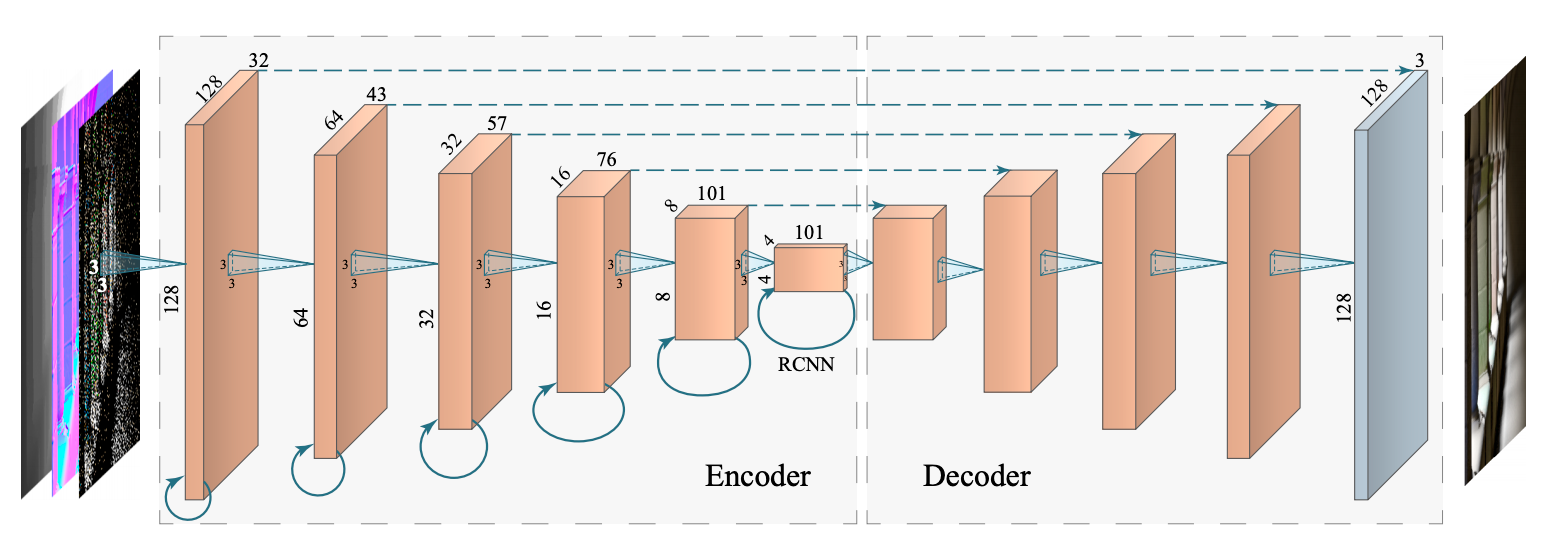
  • 输入为 G-Buffer
  • AutoEncoder
    • 对称的
    • skip connection：faster and better training
  • Recurrent Block
    • 实际跑的时候，保留前几帧的信息

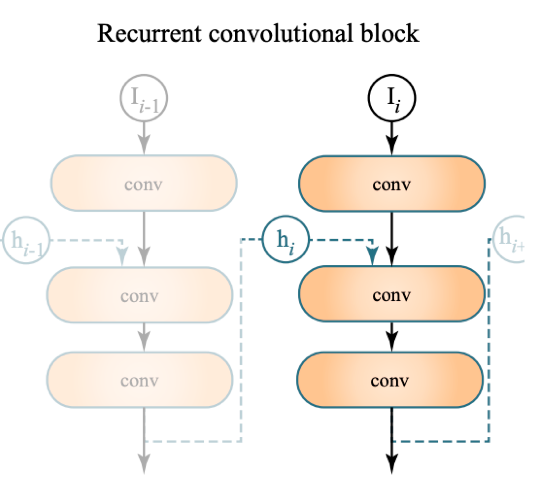
  • 训练的时候也需要用一些连续帧（不能只有单张渲染结果）
  • 没有使用 motion vector
    • 具体使用是什么内容，是神经网络学习出来的结果
  • 当时：50ms 一帧

问题

  • overblur
  • 残影
  • RAE 场景偏暗（亮了 artifacts 会增多）

SVGF vs RAE

  • 帧间抖动，一些低频噪声，看起来像沸腾的水，boiling artifacts
Quality Artifact Performance Explanability Where did the paper go
SVGF Clean Ghosting Fast Yes HPG
RAE
(when first invented)		 Overblur Ghosting Slow No SIGGRAPH

好处

  • RAE 在不同输入情况下， performance 是固定的（网络固定、计算耗时固定）
  • Nvidia 把 RAE 中的 Recurrent Block 去掉了，放到了 Optix 的光追降噪中
    • 对于稍微高一点的 spp 降噪效果非常好
    • 针对单张图片（去掉了 Recurrent Block）
  • 在 tensor core 提出之后，RAE 效果变好了