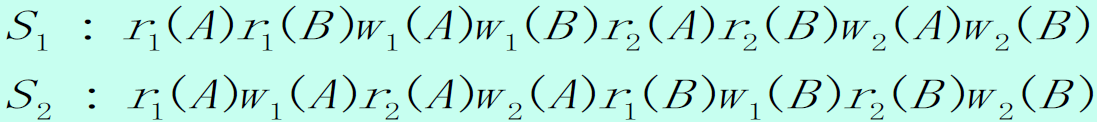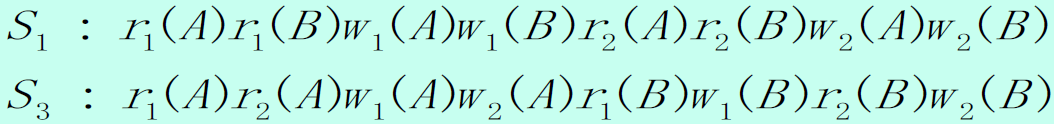数据库概论.陈立军.06.事务(3)

Posted on 2021-05-23 Edited on 2021-06-25 In DB.CLJ Views:

事务冲突可串行化（交换非冲突指令、优先图）、事务视图可串行化（从读一致性）、事务模型

事务

事务冲突可串行化

一个调度是否正确，看它执行的结果是否和某一个串行调度执行的结果相同
核心问题：
- 如何判定一个调度是可串行化的？
- 如何判定两个调度是等价的？
微观视角：交换非冲突指令
- 如何把一个调度转换为另一个等价调度？
宏观视角：从读一致性
- 如何保证每个事务在两个调度中是相同的？
- 调度内部逻辑相同，因此对于每个事务，如果输入相同则结果一致

指令顺序对调度结果的影响

考虑一个调度 S 中的两条连续指令（仅限于 read 与 write 操作）Ii 与 Ij，分别属于事务 Ti 与 Tj
考虑如下四种情况
- A：Ii=read(Q), Ij=read(Q)
- B：Ii=read(Q), Ij=write(Q)
- C：Ii=write(Q), Ij=read(Q)
- D：Ii=write(Q), Ij=write(Q)
只有 A 操作可以交换，也就是说两条指令中存在写指令则不能交换
引出冲突指令的定义

调度中的冲突指令

冲突指令
- 两条指令是不同事务在相同数据项上的操作，并且其中至少有一个是 write 指令
非冲突指令（满足一条即可）
- 都是 read 操作
- 操作不同数据项

冲突等价

如果调度 S 可以经过交换一系列非冲突指令转换成调度 S'，则称调度 S 与 S' 是冲突等价的

冲突可串行化的定义

当一个调度 S 与一个串行调度冲突等价时，则称该调度是冲突可串行化的

非冲突串行化的例子

T1	T2
read(A)
	write(A)
write(A)

冲突可串行化的判定

优先图（precedence graph）
调度 S 的优先图的构造方式
- 它是一个有向图 G=(V，E)，V是顶点集，E是边集
- 顶点集由所有参与调度的事务组成
- 边集由满足下述条件之一的边 Ti \(\to\) Tj 组成（冲突指令）
  - 在 Tj 执行 read(Q) 之前，Ti 执行 write(Q)
  - 在 Tj 执行 write(Q) 之前，Ti 执行 read(Q)
  - 在 Tj 执行 write(Q) 之前，Ti 执行 write(Q)

优先图构造例子

如果优先图中存在边 Ti \(\to\) Tj，则在任何等价于 S 的串行调度 S' 中，Ti 都必须出现在 Tj 之前
如果调度 S 的优先图中有环，则 S 是非冲突可串行化的
如果调度 S 的优先图中无环，则是冲突可串行化的
- 拓扑排序

与冲突可串行化等价的串行顺序

串行顺序可由拓扑排序得到，求出与优先图的偏序相一致的线序
优先图

graph LR;
T1-->T2;
T1-->T3;
T2-->T4;
T3-->T4;

等价串行线序

graph LR;
T1-->T2;
T2-->T3;
T3-->T4;

graph LR;
T1-->T3;
T3-->T2;
T2-->T4;

可串行化但非冲突可串行化的调度

满足上面冲突可串行化判断的调度一定是可串行化的
不满足判断的调度不一定是不可串行化的
一个例子：转账
- 在实际编写中应当尽量避免如下操作，应该按照相同的数据项的顺序进行处理
- 容易造成死锁等问题

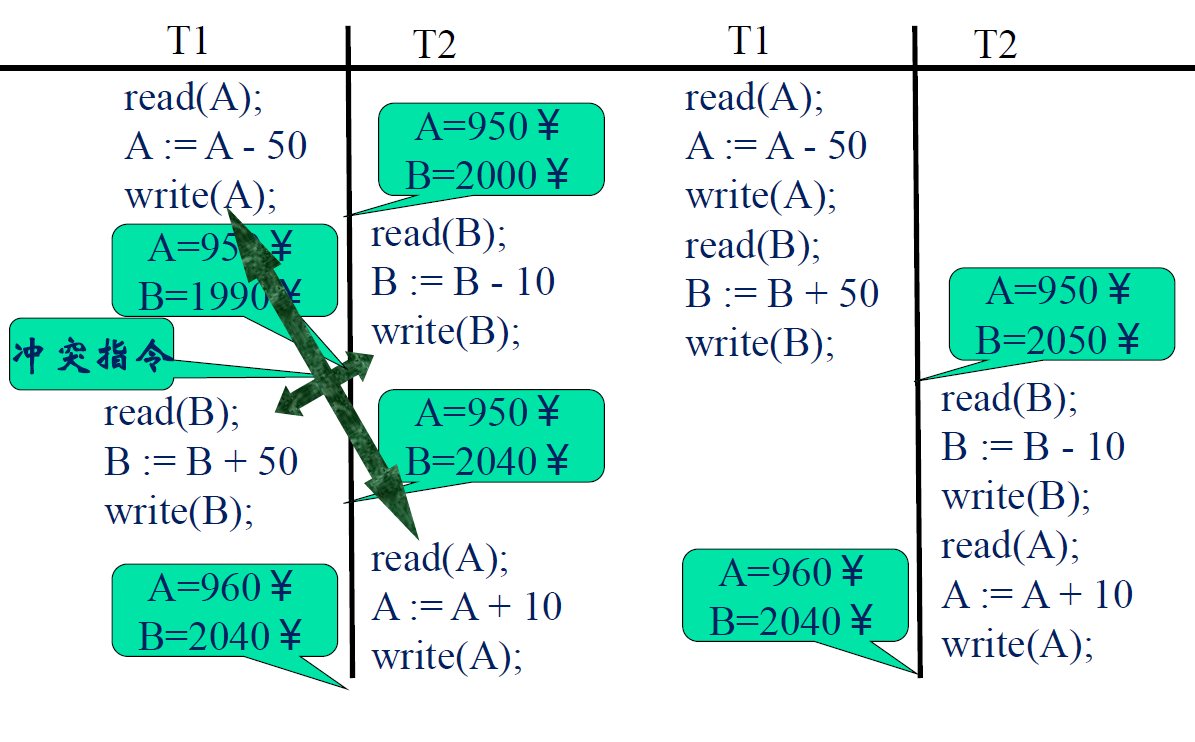
冲突可串行化的要求太苛刻了，引入视图可串行化的判定

事务视图可串行化

从读一致性

如果两个调度从读一致，则是等价的
把两个调度的 read 指令挑出来，看对应的 read 指令读到的数据是否相同
每个 read 指令往前找，离它最近的 write 相同数据项的指令，就是他读出来的值

例子 1：S1 和 S2 从读一致

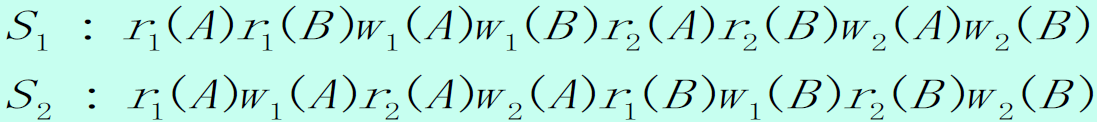
S1 中的从读关系
- r1(A) 和 r1(B) 读取的是数据库中的初值
- r2(A) 读取的是 w1(A)，r2(B) 读取 w1(B)
S2 中的从读关系
- r1(A) 和 r1(B) 读取的是数据库中的初值
- r2(A) 读取的是 w1(A)，r2(B) 读取 w1(B)

例子 2：S1 和 S3 从读不一致

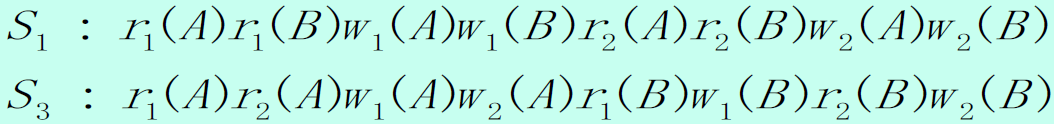
S1 中的从读关系
- r1(A) 和 r1(B) 读取的是数据库中的初值
- r2(A) 读取的是 w1(A)，r2(B) 读取 w1(B)
S3 中的从读关系
- r1(A) 和 r1(B) 读取的是数据库中的初值
- r2(A) 读取的是数据库中的初值
- r2(B) 读取 w1(B)

视图等价的调度

考虑关于某个事务集的两个调度 S，S'，若调度 S，S' 满足以下条件，则称它们是视图等价的
- 数据库初值 \({\buildrel{S}\over\longrightarrow}\) ri(Q)，数据库初值 \({\buildrel{S'}\over\longrightarrow}\) ri(Q)
- wj(Q) \({\buildrel{S}\over\longrightarrow}\) ri(Q)，wj(Q) \({\buildrel{S'}\over\longrightarrow}\) ri(Q)
- wj(Q) \({\buildrel{S}\over\longrightarrow}\) 数据库终值，wj(Q) \({\buildrel{S'}\over\longrightarrow}\) 数据库终值
前两条保证从读一致性
最后一条保证两个调度得到最终相同的系统状态

视图等价的例子

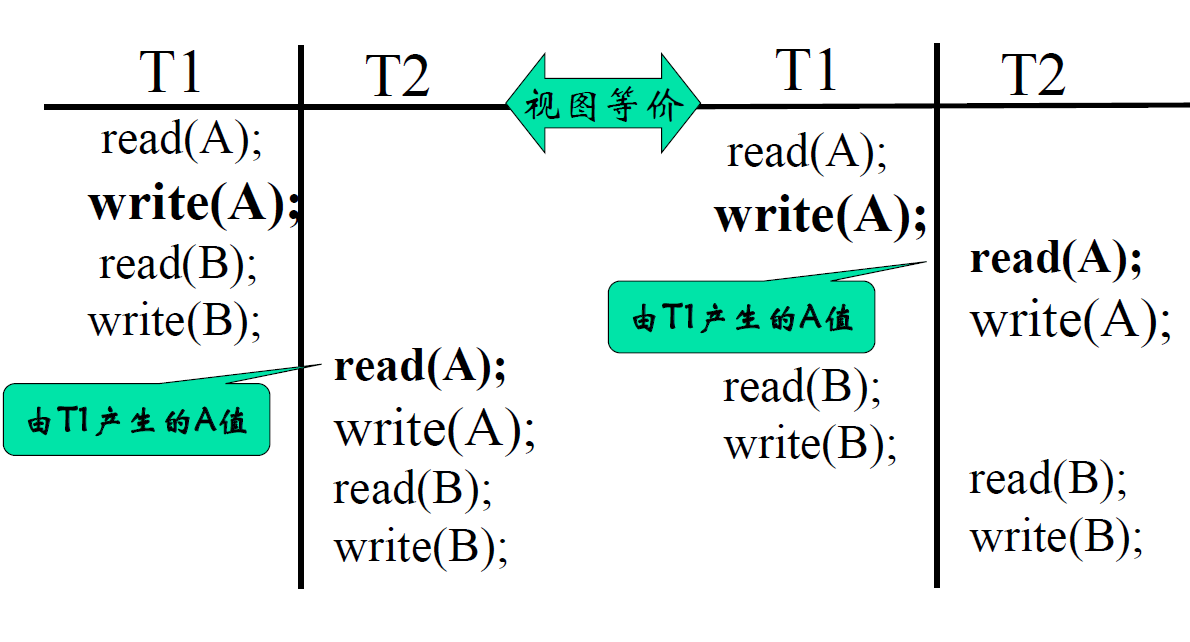
视图可串行化

如果某个调度视图等价于一个串行调度，则称该调度是视图可串行化的
冲突可串行化调度一定是视图可串行化的
- 冲突可串行化的调度一定满足从读一致性
- 交换一系列非冲突指令，不会破坏从读一致性
存在视图可串行化但非冲突可串行化的调度

盲目写操作：不读就写

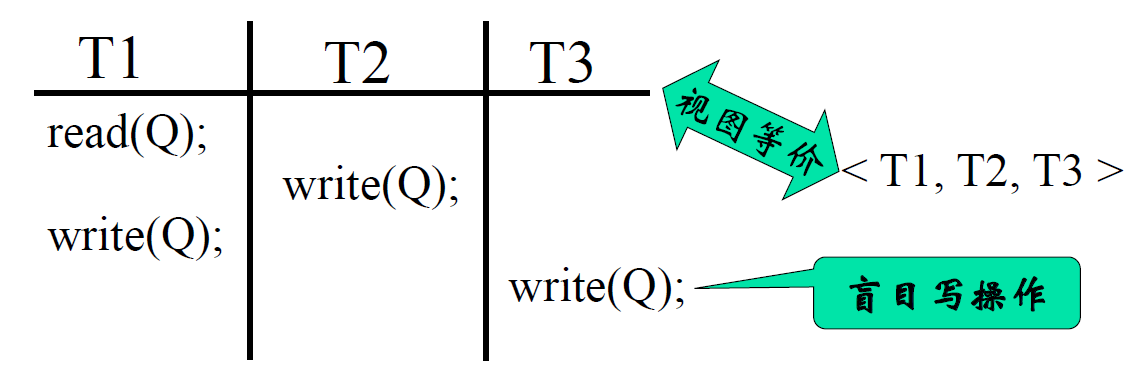
视图可串行化判定

思想

找出所有的从读关系
如果有其他事务对某个数据项有写操作，这个写操作不能破坏这个数据项的从读关系

算法

设调度 S 包含了事务 {T1,T2, ... ,Tn} ，设 Tb,Tf 是两个虚事务，其中 Tb 为 S 中所有 write(Q) 操作，Tf 为 S 中所有 read(Q) 操作。在调度 S 的开头插入 Tb ，在调度 S 的末尾插入 Tf，得到新的调度 S'
- 如果 Tj 读取 Ti 写入的数据项的值，则加入边 Ti \({\buildrel{0}\over\longrightarrow}\) Tj
- 删除所有关联无用事务的边。如果在优先图中不存在从 Ti 到 Tf 的通路，则 Ti 是无用事务
- 对于每个数据项 Q，如果 Tj 读取 Ti 写入的 Q 值，Tk 执行 write(Q) 操作且 Tk \(\ne\) Tb，则
  - 如果 Ti = Tb 且 Tj \(\ne\) Tf，则在带标记的优先图中插入边 Tj \({\buildrel{0}\over\longrightarrow}\) Tk
  - 如果Ti \(\ne\) Tb 且 Tj=Tf，则在带标记的优先图中插入边 Tk \({\buildrel{0}\over\longrightarrow}\) Ti
  - 如果 Ti \(\ne\) Tb且 Tj \(\ne\) Tf，则在带标记的优先图中插入边 Tk \({\buildrel{p}\over\longrightarrow}\) Ti 与 Tj \({\buildrel{p}\over\longrightarrow}\) Tk
    - 其中 p 是一个唯一的，在前面边的标记中未曾用过的大于 0 的整数

算法解释

读数据库初值的，就是读取 Tb 的
最终加入一个 Tf，表示读数据库终值

简单的算法操作

找到所有的从读关系，加边（包括读初值、写中止）
对剩下的写操作做分析，不能破坏上面的从读关系
- 只能加前面 / 只能加后面：标记 0
- 否则加两条边，并标记 p

算法解释（例子1）

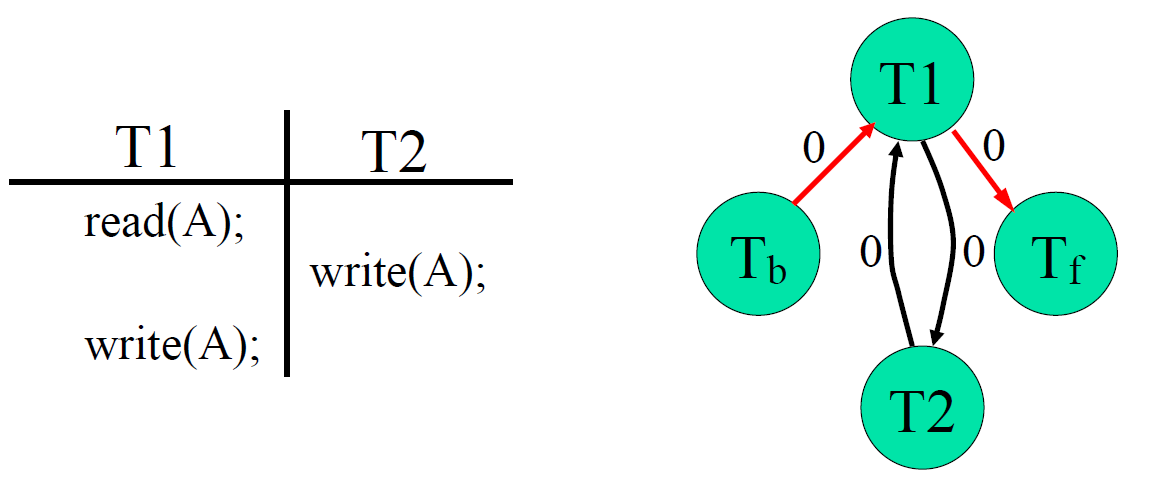
找出从读关系（红边）
- read(A) 读取数据库初值，加上一条边（Tb \(\to\) T1）
- write(A) 写数据库终值，加上一条边（T1 \(\to\) Tf）
对从读关系进行判断，找到和从读关系操作数据项相同的 write 操作
- write(A) 不能破坏边（Tb \(\to\) T1）的从读关系，因此 T2 只能在 Tb 的前面（这不允许，Tb是第一个事务）或者 T1 的后面
- write(A) 不能破坏边（T1 \(\to\) Tf）的从读关系，因此 T2 只能在 T1 的前面或者 Tf 的后面（这不允许，Tf 是最后一个事务）
结果有环，不是视图可串行化的

例子 2

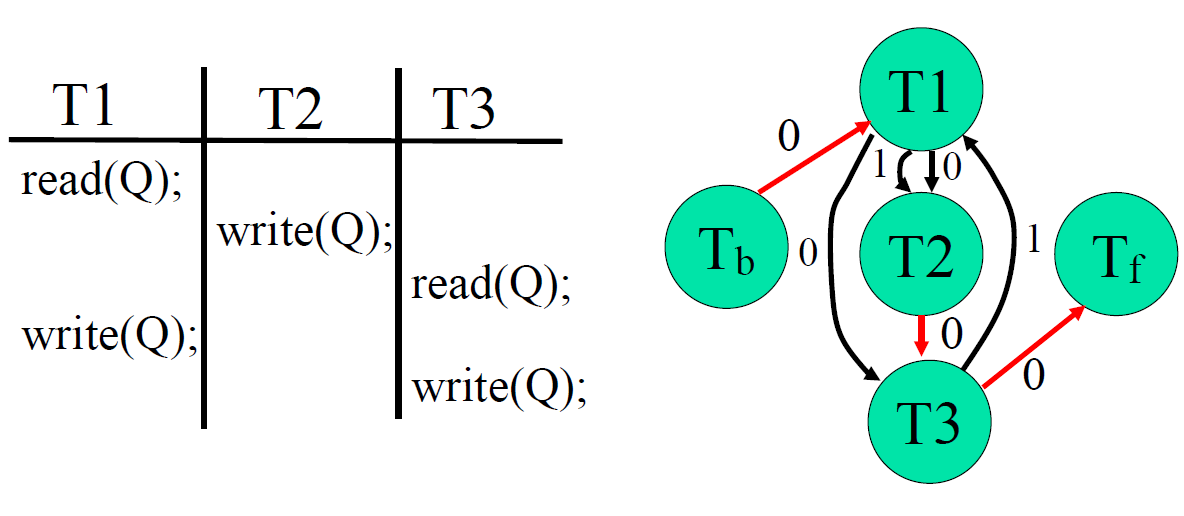
按照上面的算法构造优先图
- 标号相同且不为 0 的边，有一条边成立即可
判定
- 每个优先图包含标号大于 1 的边对中的一条
- 判定准则：只要有一个优先图无环，则调度是视图可串行化的

左图无环，是视图可串行化的

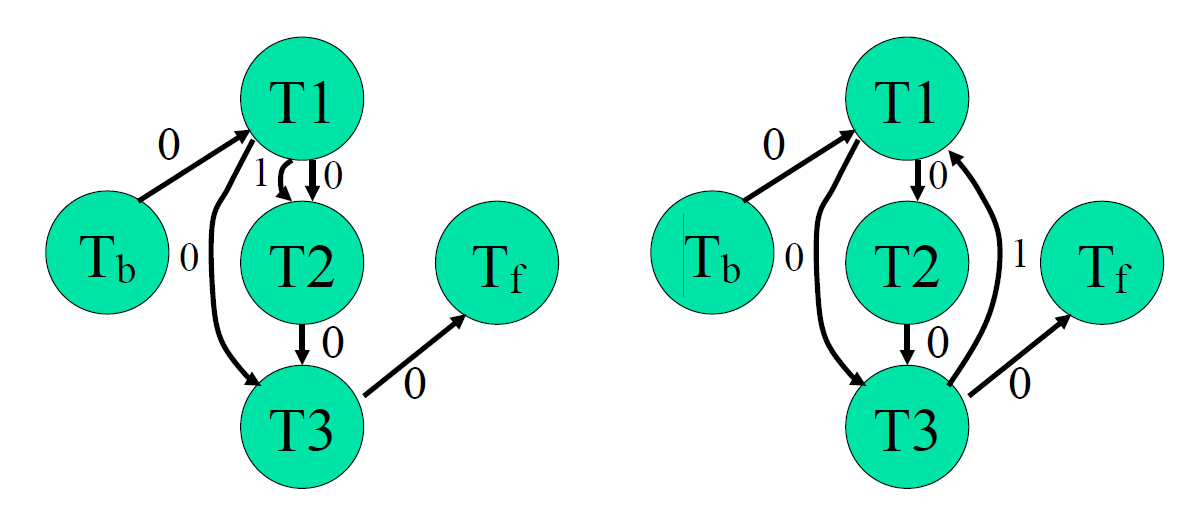
视图可串行化判定示例

满足上面视图可串行化判断的调度一定是可串行化的
不满足判断的调度不一定是不可串行化的
例子
- 另外一种判定方法：如下调度与任意一个串行调度都不是视图等价的
  - T1, T2
  - T2, T1

T1	T2
read(A)
A := A - 50
write(A)
	read(B)
	B := B - 10
	write(B)
read(B)
B := B + 50
write(B)
	read(A)
	A := A + 10
	write(A)

事务模型

平面事务

一层结构

1	begin transaction ... commit

平面事务的缺点
- 不能部分回滚
某些应用场合有部分回滚的需求

部分回滚应用场合

确定旅行路线
- 某条线路不通应该回滚到上一个分支点，而不是回滚整个事务
批量更新
- 如银行结算利息，可以把更新每个帐号作为一个事务，也可以把更新所有帐号作为一个事务
- 一部分记录更新后，做一个保存点

保存点

begin_transaction()
    S1;
    sp1 := create_savepoint();
    ...
    Sn;
    spn:= create_savepoint();
    ...
    if(condition){
        rollback(spi);
        ...
    }
    ...
commit();

一个例子

begin tran
----转账部分
update accounts
set amounts=amounts-100
where account_id='A'
update accounts
set amounts=amounts+100
where account_id='A'

----结算利息, 然后撤销
save tran add_interest --保存点
update accounts
set amounts=amounts*1.02
select * from accounts
rollback tranadd_interest
commit tran

分布式事务

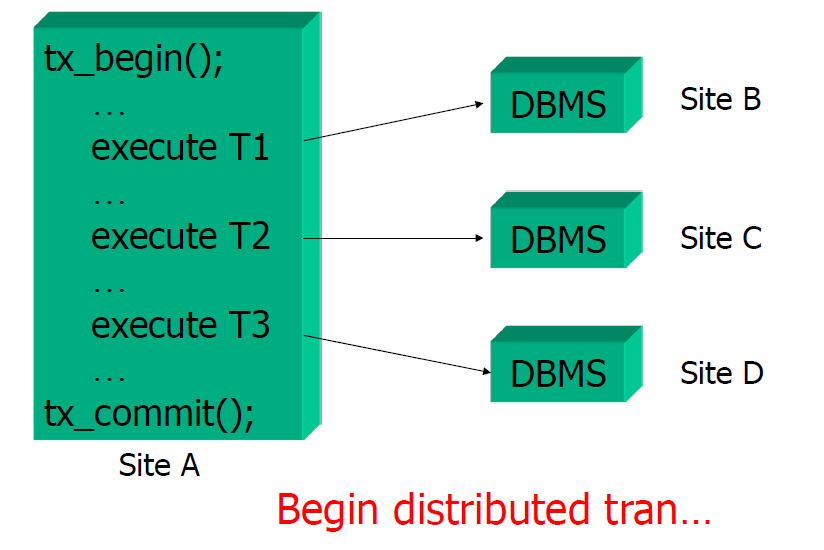
Moss 的嵌套事务模型

嵌套事务是一棵事务树，子树可以是嵌套的也可以是平面的
叶结点事务是平面事务，从根结点到各个叶结点的距离可以是不同的
根结点事务称作顶层事务，其他称作子事务
子事务可以提交也可以回滚，但它的提交并不起作用，除非它的父事务提交
- 只有根结点的提交才会使得所有子事务提交
树中任何一个事务的回滚导致它的所有子事务的回滚
子事务具有一般事务的 A,C,I 特性，但不具有 D 特性
实际工作只发生在叶结点事务中，只有它们可以访问数据库，发送消息等
- 上层事务只是组织控制流以及决定什么时候该激活哪个子事务

规则

提交规则
- 当子事务提交时，它的结果只能被它的父事务所访问
- 只有当一个子事务提交了，并且它的一直到根的所有祖先也都提交了，该子事务才最终提交
- 因此，只有根结点提交了，所有子事务才会提交
回滚规则
- 如果任何一个嵌套层次的事务回滚了，它的所有子事务也都要回滚，不管它们当前是否已经提交
- 因此，如果根结点回滚，整个嵌套事务也就回滚
可见规则
- 当子事务提交后，它的修改对其父事务是可见的，而对其兄弟是不可见的
- 父事务的任何对象对其子事务都是可访问的

例子

create table TestNestTrans(Col char(3))
create proccedure TransProc @CharCol char(3)
as
begin transaction InProc
    insert into TestNestTrans values(@CharCol)
commit transaction InProc

begin transaction OutOfProc
    exec TransProc 'aaa'
rollback transaction OutOfProc

exec TransProc 'bbb'
select * from TestTrans
--最终 TestNestTrans 表中只有元组 bbb

工作流（workflow）

实现某种商业目的的一组相关活动（或步骤）
- 银行或保险公司的贷款申请或保险索赔
- 一次科技会议的规划(邀请、评论、通知等等)
- 购买房地产的行政程序
- 病人在医院中的“行程”
工作流使得机构把他们重复的、一成不变的处理自动化，同时保持灵活性，根据不断变化的商业需求来很快调整处理过程
工作流可能跨越不同的负责人和不同的、独立的信息系统，甚至跨越不同的企业
银行借贷工作流

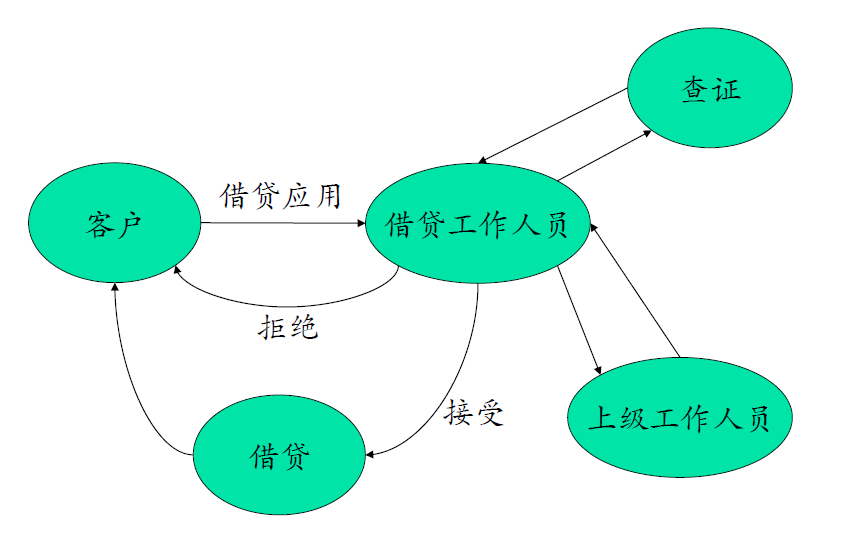
工作流任务间的依赖关系

其他任务的执行状态
- 任务 tj 结束了，任务 ti 才能开始
其他任务的输出值
- 如果任务 tj 返回一个大于 20 的值，则任务 ti 可以开始
- 如果秘书审批任务返回 OK，则经理审批任务可以开始
外部时间修改的外部变量
- 上午9点以后任务 ti 才能开始
- 在任务 tj 完成后的 24 小时内必须开始任务 ti

工作流的执行

工作流执行
- 提交的可接受终止状态
- 中止的可接受终止状态
整个工作流作为一个事务？
- 工作流持续时间很长
- 每个活动作为一个事务？
如何取消一个活动？补偿事务

长事务

运行时间过长，不能采用传统的封锁机制
业务事务：涉及多个相关步骤、运行较长时间
例如购物包括以下若干步骤
- 订购商品、商议价格、确定发货日期、确认发货、开具发票、收到货款、发货、...
不能用普通事务实现，否则锁死很久

典型例子

传统的 DBMS 应用
- 计算所有银行账户余额
设计系统
- 设计被分为不同部分，不同设计者同时工作在不同部分上
工作流系统

特点

持续时间长
暴露未提交的数据
子任务
- 中止其中某个子任务，而不必中止整个事务
可恢复性
- 不要将整个事务撤销，而恢复到系统崩溃之前的某一状态，使丢掉的工作尽量少
性能
- 响应时间 vs 事务吞吐量

Saga

Saga：构成长事务的一系列动作
一个图，其结点是动作或中止及完成结点，弧连接结点对
- 中止及完成结点称为终止结点
关于动作从哪个结点开始的指示，称为开始节点
Saga 的并发控制
- 每个动作是一个一个短事务，采用传统的并发控制
- 整个事务的完整性由补偿事务来保证
  - 整个事务，即任何通向终止结点的路径通过补偿事务来管理，也即每个结点上短事务的逆（用于撤销回滚）

Service Broker

转化为异步的消息队列
每个部门处理订单的一部分，每个部分处理完自己的短事务之后，打包成一个消息传递给下一个部门
可靠的（reliable）、有序的（in order）、异步的（asynchronous）