数据库概论.陈立军.05.关系规范化(3)
模式分解
- 例子:给定一个关系模式,通过模式分解解决异常
- 关系模式:\(R(ABCD;A\to B,B\to C)\)
- 分解一
- \(R_1(AB;A\to B),R_2(BC;B\to C)\)
- 不是正确的分解,缺失了属性 \(D\)
- 分解二
- \(R_1(ABD;A\to B),R_2(BC;B\to C),R_3(BD)\)
- 不是正确的分解,\(R_3\) 包含在 \(R_1\) 中,没必要
- 分解三
- \(R_1(AB;A\to B),R_2(AC),R_3(AD)\)
- 不是正确的分解,和原来的关系模式函数依赖不等价(\(A\to C\))
- 分解四
- \(R_1(AB;A\to B),R_2(AC;A\to C),R_3(AD)\)
- 正确
模式分解的定义
- 属性上来看
- 子模式的属性集的并集和原来相同
- 子模式的属性集之间不能有包含关系
- 函数依赖上看
- 原来函数依赖集要正确的投影到子模式的属性集上面
函数依赖在属性集上的投影
- 函数依赖集 \(F\) 在属性集 \(U_i\) 上的投影定义为:\(F_i=\{X\to Y|X\to Y\in F^+\land XY\subseteq U_i\}\)
例子1
- 求 \(F=\{A\to B, B\to C, C\to D\}\) 在 \(S(ACD)\) 上的投影
- 先求出闭包
- \(A_F^+=ABCD,C_F^+=CD,D_F^+=D\)
- 写出函数依赖
- 需要考虑二元(多元)
- \(A_F^+\) 已经是全集了,于是不需要考虑 \(A\) 和其他的组合
- \((CD_F)^+=CD\),于是也不需要了
- \(A\to C,A\to D,C\to D\)
- 需要考虑二元(多元)
- 消除冗余依赖
- \(A\to C,C\to D\)
例子2
- 计算下面函数依赖集在 \(S(ABC)\)
上的投影
- \(F=\{AB\to DE,C\to E,D\to C,E\to A\}\)
- \(F=\{A\to D,BD\to E,AC\to E,DE\to B\}\)
- \(F=\{AB\to D,AC\to E,BC\to D,D\to A,E\to B\}\)
\((1)\;F=\{AB\to DE,C\to E,D\to C,E\to A\}\)
\({\color{red}\{C\to A,AB\to C,BC\to A\}}\)
\(A_F^+=A\)
\(B_F^+=B\)
\(C_F^+=CEA\)
\((AB)_F^+=ABDEC\)
\((AC)_F^+=ACE\)
\((BC)_F^+=BCEAD\)
\((2)\;F=\{A\to D,BD\to E,AC\to E,DE\to B\}\)
- \({\color{red}\{AC\to B\}}\)
- \(A_F^+=AD\)
- \(B_F^+=B\)
- \(C_F^+=C\)
- \((AB)_F^+=ABDE\)
- \((AC)_F^+=ACDEB\)
- \((BC)_F^+=BC\)
\((3)\;F=\{AB\to D,AC\to E,BC\to D,D\to A,E\to B\}\)
- \({\color{red}\{AC\to B,BC\to A\}}\)
- \(A_F^+=A\)
- \(B_F^+=B\)
- \(C_F^+=C\)
- \((AB)_F^+=ABD\)
- \((AC)_F^+=ACEBD\)
- \((BC)_F^+=BCDAE\)
模式分解的定义
- 关系模式 \(R(U , F)\)
的一个分解是指
- \(\rho=\{R_1(U_1,F_1),\cdots,R_n(U_n,F_n)\}\)
- 其中 \(U=\bigcup_{i=1}^{n}U_i\),并且没有 \(U_i\subseteq U_j,1\le i,j\le n\)
- \(F_i\) 是 \(F\) 在 \(U_i\) 上的投影
- 模式分解的代数运算
- 分解:投影
- 还原:自然连接
模式分解的目标
- trade off
- 达到更高级的范式
- 无损连接分解
- 保持函数依赖
模式分解中的问题
异常
- 分解的过于完全:丢失信息
违约/违章
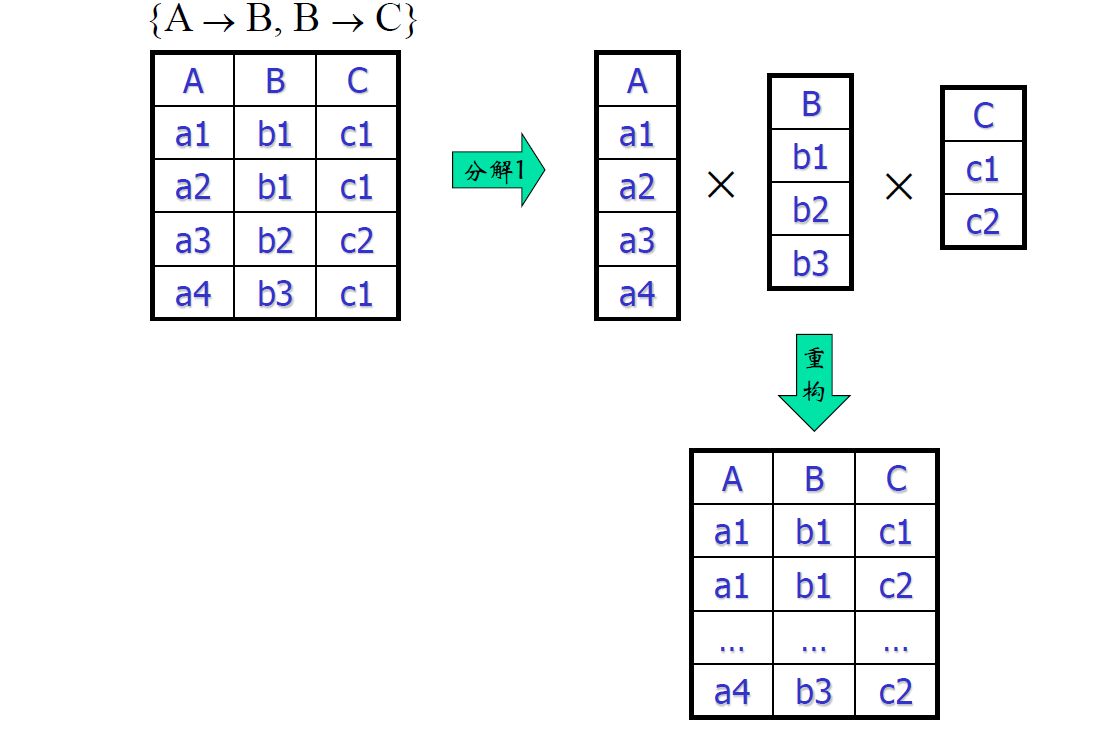
- 在分解之后的表中执行插入操作,重构的时候可能违反原始表的函数依赖
- 问题是丢失了函数依赖
- \(A\to B,A\to C\) 推导不出原来的 \(B\to C\)
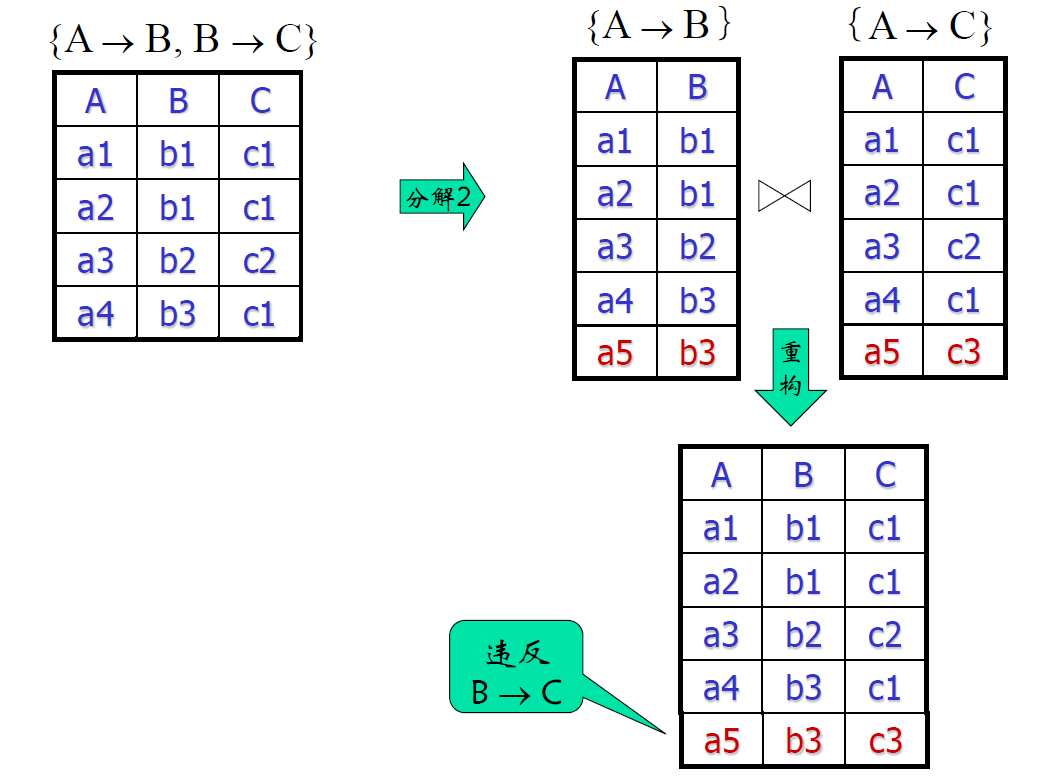
有损
- 有损分解:信息损失了
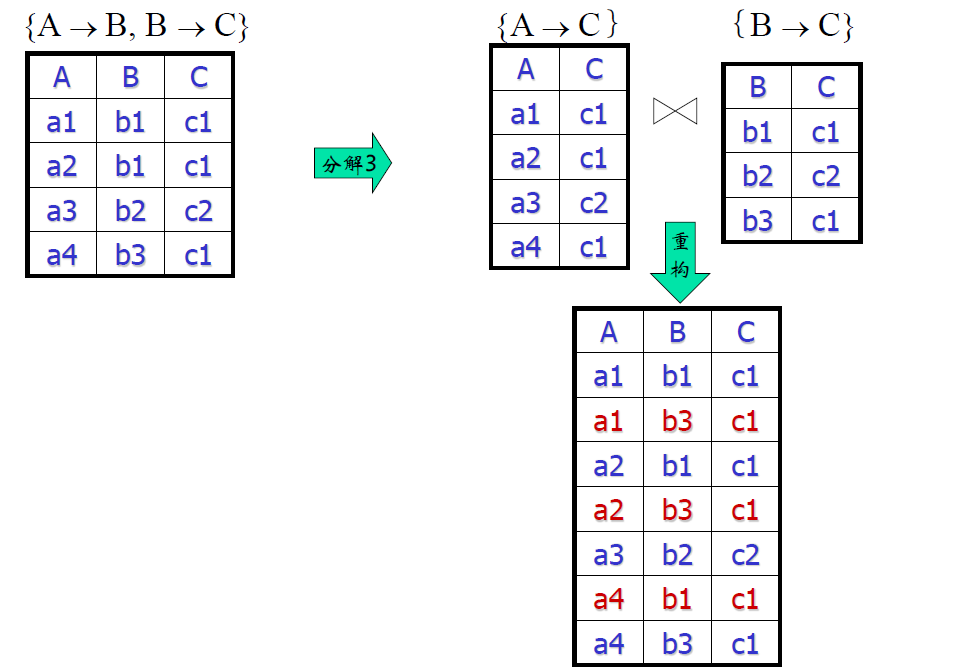
正确的分解
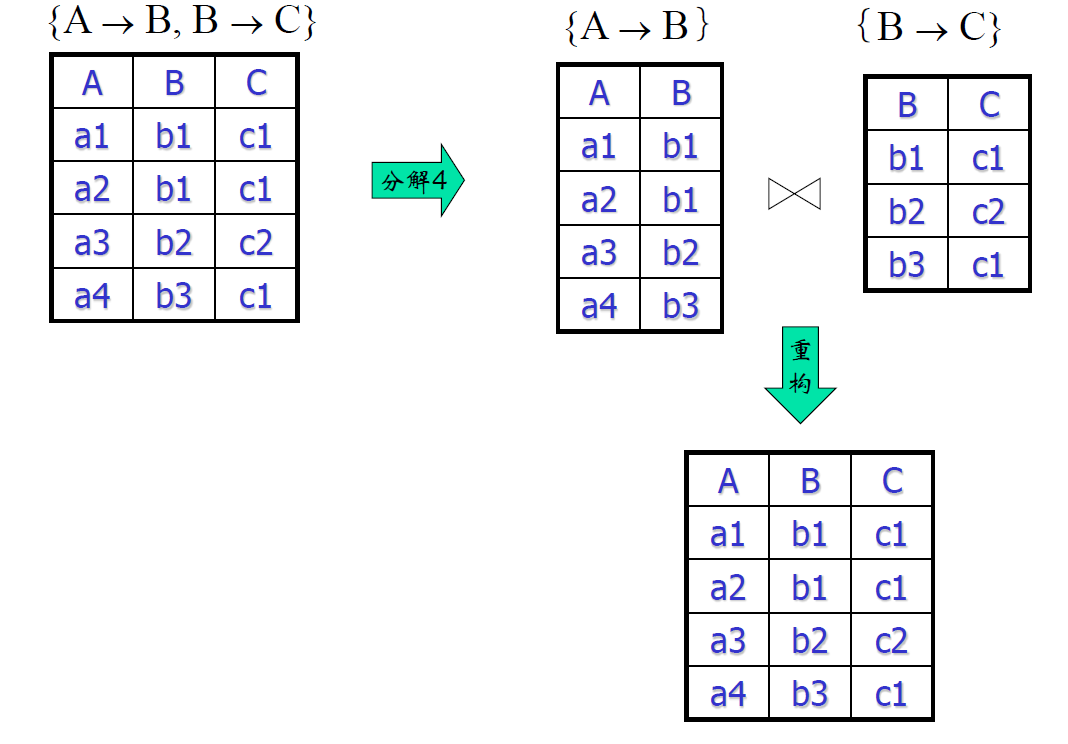
- 有损比违章害处更大,违章的数据可以通过检查剔除
保持函数依赖的分解
- 设关系模式 \(R(U , F)\)
的一个分解是
- \(\rho=\{R_1(U_1,F_1),\cdots,R_n(U_n,F_n)\}\)
- 如果 \(F^+=(\bigcup_{i=1}^nF_i)^+\)
- 则称 \(\rho\) 是保持函数依赖的分解
- 等价于验证 \(F\subseteq (\bigcup_{i=1}^nF_i)^+,F_i\subseteq F\)
- 由于 \(F_i\) 都是由 \(F\) 导出的,我们只需要验证 \(F\) 中的函数依赖能够被 \(\bigcup F_i\) 导出即可
丢失函数依赖的分解实例
- \(U=\{CITY,ST,ZIP\},F=\{(CITY,ST)\to ZIP,ZIP\to CITY\}\)
- 分解如下
- \(U_1=\{ST,ZIP\},F1=\{\}\)
- \(U_2=\{CITY,ZIP\},F2=\{ZIP\to CITY\}\)
- 丢失了函数依赖 \((CITY,ST)\to ZIP\)
- 插入数据导致的问题
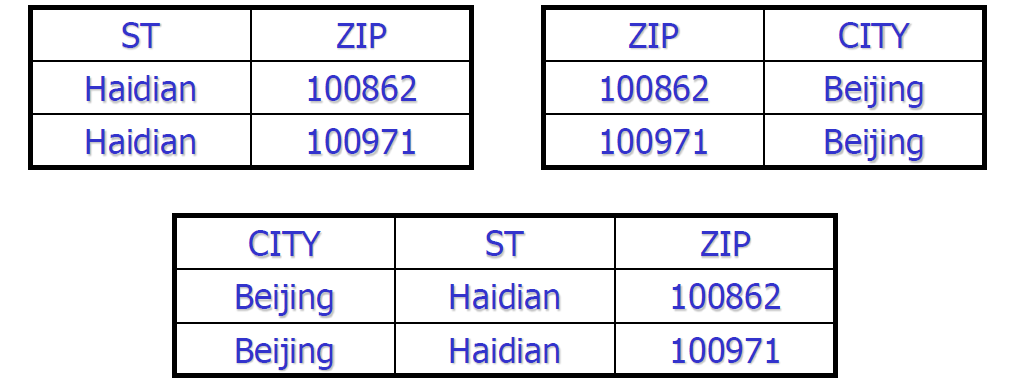
有损分解的例子
- 构造方法:公共属性上相同值多一些
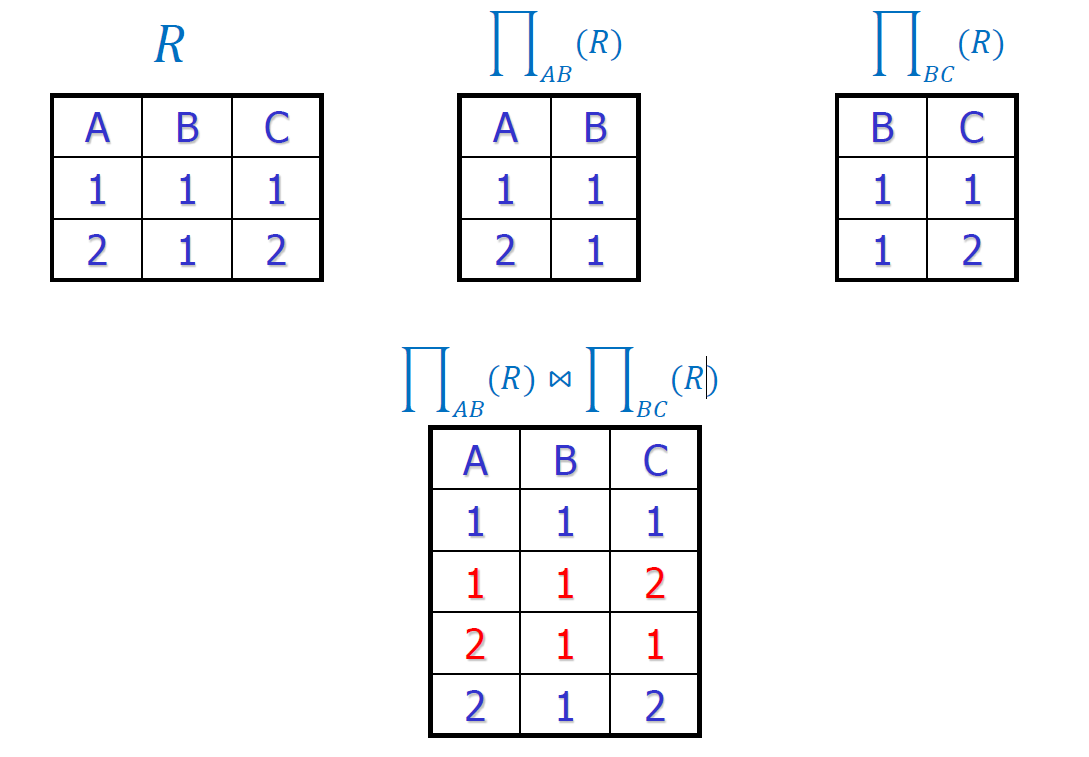
无损连接分解
定义
- 设关系模式 \(R(U , F)\)
的一个分解是
- \(\rho=\{R_1(U_1,F_1),\cdots,R_n(U_n,F_n)\}\)
- \(r\) 是 \(R\) 的任意一个关系实例
- 定义 \(m_{\rho}(r)=\prod_{U_i}(r)\)
- 若 \(m_{\rho}(r)=r\),则称 \(\rho\) 是 \(R\) 的一个无损分解
无损连接分解的判别算法
- \(U=\{A_1,A_2,\cdots,A_n\}\)
- \(\rho=\{R_1(U_1,F_1),\cdots,R_k(U_k,F_k)\}\)
(1) 建立一个 \(n\) 列 \(k\) 行的矩阵 TB
- 填充矩阵
- \(TB=\{C_{ij}|若A_i\in U_i,C_{ij}=a_j,否则C_{ij}=b_{ij}\}\)
(2) 对 \(F\) 中每一个函数依赖 \(X\to Y\)
- 若 TB 中存在元组 \(t_1,t_2\),使得 \(t_1[X]=t_2[X],t_1[Y]\ne t_2[Y]\)
- 则对每一个 \(A_i\in Y\)
进行如下操作
- 若 \(t_1[A_i],t_2[A_i]\) 中有一个等于\(a_j\),则另一个也改为 \(a_j\)
- 否则取 \(t_1[A_i]=t_2[A_i]\)(\(t_2\) 的行号小于 \(t_1\))
(3) 反复执行 (2),直至如下情况发生
- TB 中出现一行全为 \(a_1,a_2,\cdots,a_n\)的一行(无损分解)
- TB 不再变化,而且没有一行为 \(a_1,a_2,\cdots,a_n\)(有损分解)
一个算法的例子
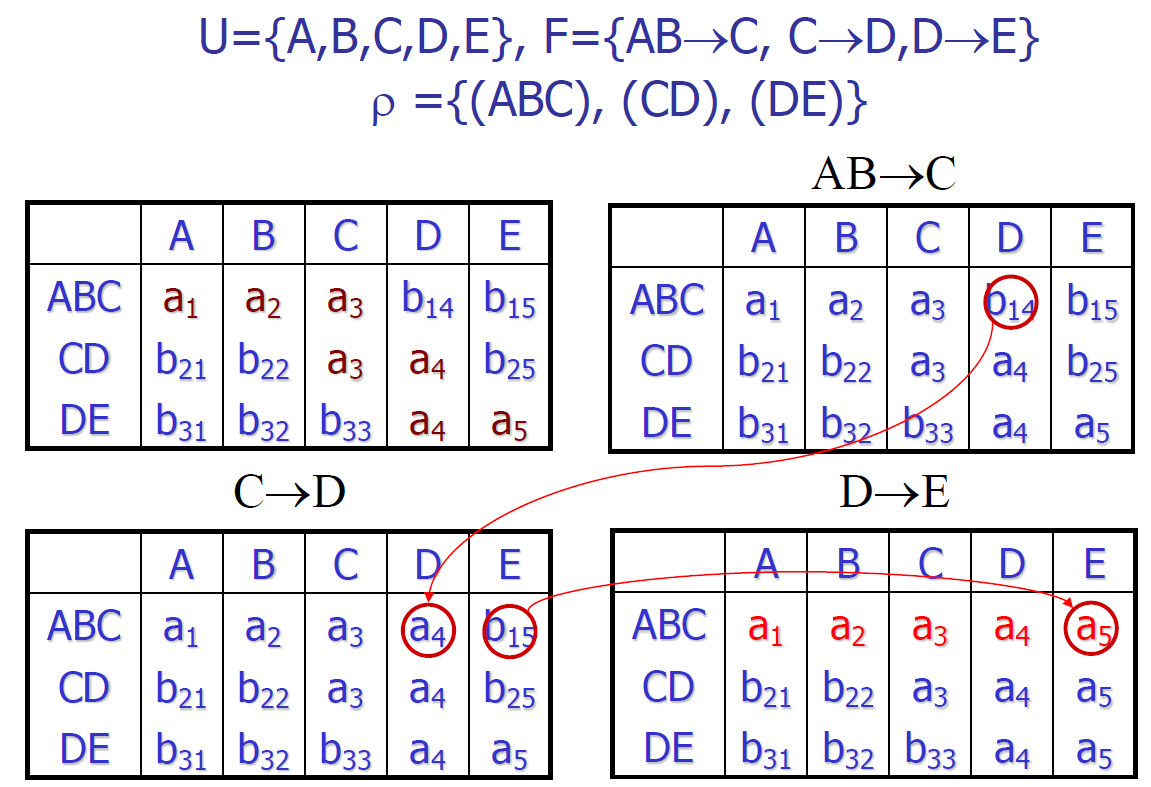
分解为两个关系模式的无损分解
- 关系模式 \(R(U),U_1\cup U_2 = U\)
- \(r\) 是 \(R\) 上的任一关系,\(r_1=\prod_{U_1}(r),r_2=\prod_{U_2}(r)\)
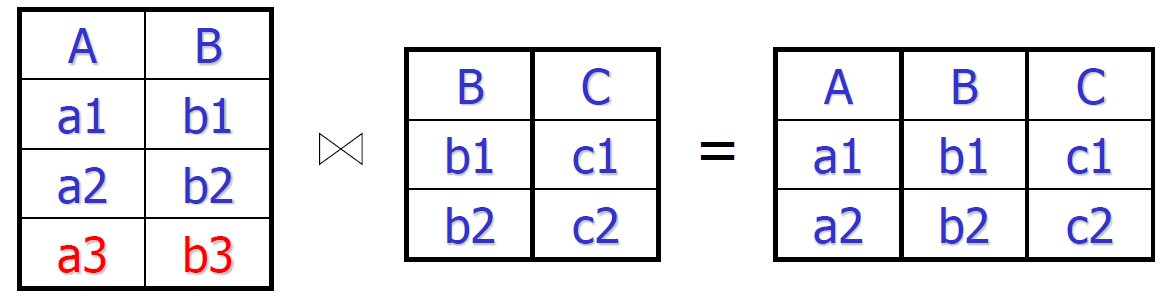
- 若\(r = r_1\bowtie r_2\),则称 \(\{U_1,U_2\}\) 是 \(U\) 的一个无损连接分解
判定
- \(\rho\) 是无损连接分解 \(\Leftrightarrow\) \(U_1\cap U_2\to U_1−U_2\) 或 \(U_1\cap U_2\to U_2−U_1\)
- 使用之前的判定算法做一个简单的证明
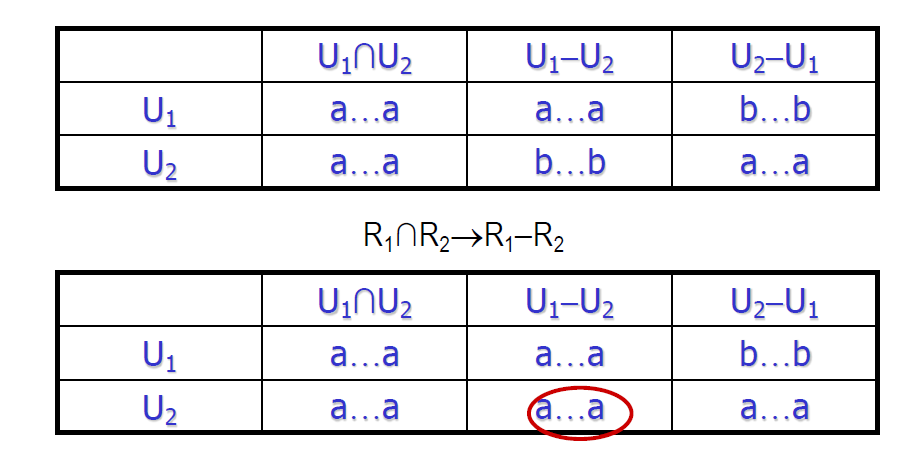
- 在这里没有证明, 如果是无损的,则能推出上述函数依赖
例子
- \(R=ABC,F=\{A\to B\}\)
- 分解一:\(\rho_1={R_1(AB),R_2(AC)}\)
- \(R_1\cap R_2=A,R_1-R_2=B\)
- 由 \(A\to B\),得到 \(\rho_1\)
- 是无损连接分解
- 分解二:\(\rho_2=\{R_1(AB),R_2(BC)\}\)
- \(R_1\cap R_2=B,R_1-R_2=A,R_2-R_1=C\)
- \(B\to A,B\to C\) 均不成立
- 不是无损连接分解
达到 BCNF 无损连接分解算法
- BCNF:对于每个子模式,所有的函数依赖的左边都是码
算法流程
- 给定关系模式 \(R(U,F)\)
- 令 \(\rho=R(U,F)\)
- 检查 \(\rho\) 中各关系模式是否属于BCNF,若是,则算法终止
- 设 \(\rho\) 中 \(R_i(U_i,F_i)\) 不属于 BCNF
- 则存在函数依赖 \(X\to A\in F_i^+\),且 \(X\) 不是 \(R_i\) 的码
- 将 \(R_i\) 分解为 \(\sigma=\{S_1(U_1),S_2(U_2)\}\)
- 其中 \(U_1=XA,U_2=U_i-A\)
- 以 \(\sigma\) 代替 \(R_i\),返回到 (2)
- 结果一定能够达到 BCNF
- 结果一定是无损的,可以通过上面 ”分解为两个关系模式的无损分解算法“
证明
- \(U_1\cap U_2=X\)
- \(U_1-U_2=A\)
- \(X\to A\)
一个例子
- 码是 AD,A 不是码,B 不是码
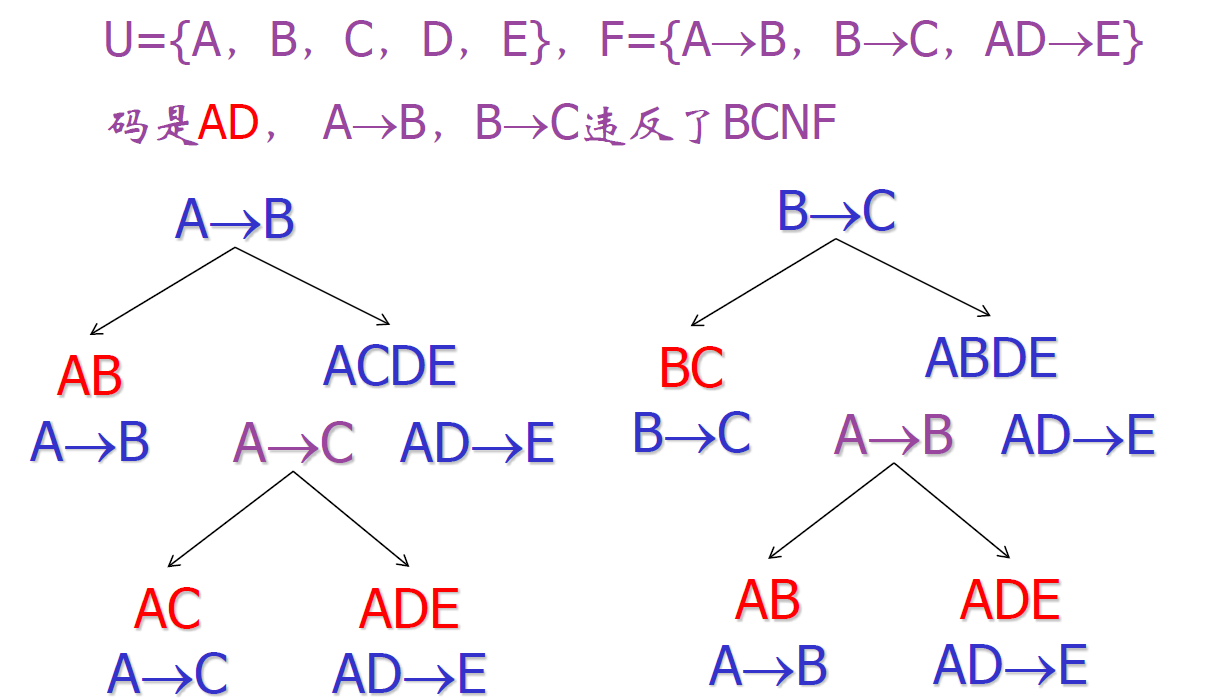
- 当原来的关系模式中,存在多个函数依赖不满足 BCNF,处理的先后顺序会影响最终的结果
- 如何构造一个有 N 种 BCNF 分解结果的关系模式?
- 一个例子:3
- \(A\to D,B\to D,C\to D\),码是 \(ABC\)
关于BCNF分解的额外讨论
- \(R(ABCD),FD=\{A\to B,A\to C\}\)
- 码是 \(AD\),分解为 BCNF
- 分解结果为 \(R_1(AB),R_2(AC),R_3(AD)\)
- \(R_1,R_2\) 没必要分开
- 优化方法:基于 \(X\to A\) 的 BCNF
分解,将右边扩展为 \(X\) 的闭包
- 分解结果为 \(R_1(ABC),R_2(AD)\)
达到 4NF 无损连接分解算法
- 给定关系模式 \(R(U,F)\)
- 令 \(\rho=R(U,F)\)
- 检查 \(\rho\) 中各关系模式是否属于BCNF,若是,则算法终止
- 设 \(\rho\) 中 \(R_i(U_i,F_i)\) 不属于 BCNF
- 则存在非平凡多值依赖 \(X\to\to A\),且 \(X\) 不是 \(R_i\) 的码
- 将 \(R_i\) 分解为 \(\sigma=\{S_1(U_1),S_2(U_2)\}\)
- 其中 \(U_1=XA,U_2=U_i-A\)
- 以 \(\sigma\) 代替 \(R_i\),返回到 (2)
- 一个例子
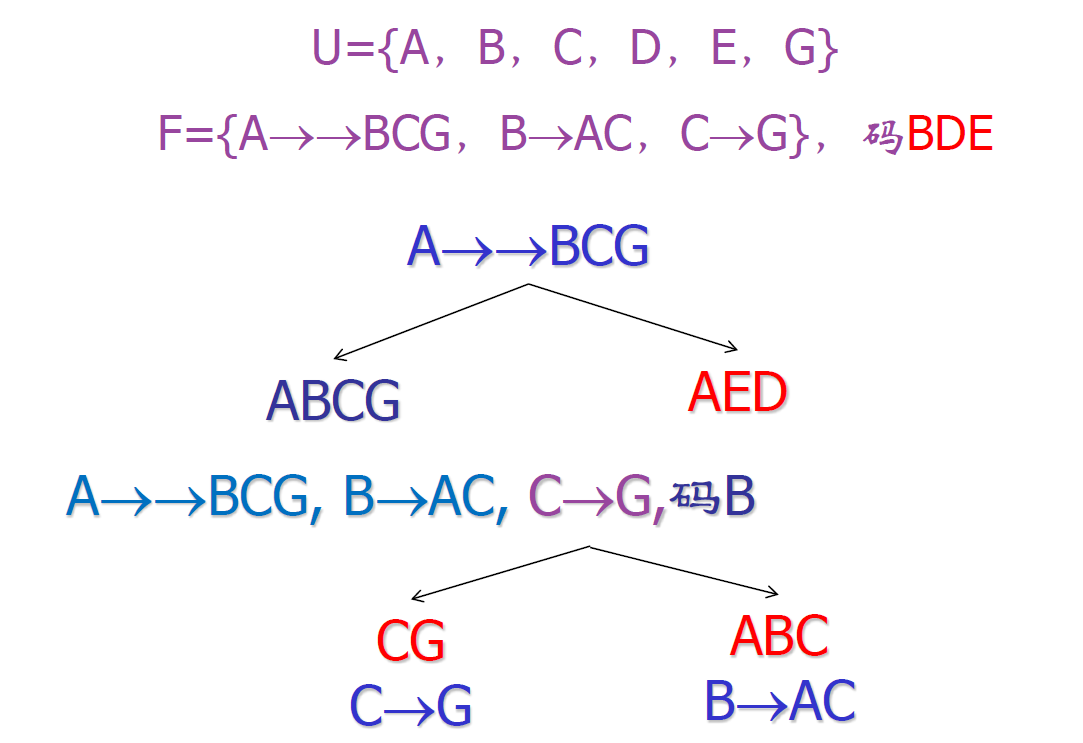
丢失函数依赖的 BCNF 分解
- 若要求分解保持函数依赖,那么分解后的模式总可以达到 3NF,但不一定能达到 BCNF
- 例子
- \(U=(sno, tno, cno),F=\{(sno, cno)\to tno, tno\to cno\}\)
- 不属于BCNF,分解为 \(U_1=(sno, tno),U_2=(tno, cno),F_2=\{tno\to cno\}\)
- 丢失了函数依赖 \((sno, cno)\to tno\)
达到 3NF 保持函数依赖的分解
- 求 \(F\) 的最小覆盖 \(F_{min}\)
- 找出不在 \(F_{min}\) 中出现的属性,将它们构成一个关系模式,并从 \(U\) 中去掉它们(剩余属性仍记为\(U\))
- 若有 \(X\to A\in F_{min}\),且 \(XA=U\),\(\rho=\{R\}\),算法终止
- 对 \(F_{min}\)
按具有相同左部的原则进行分组(设为 \(k\) 组)
- 每一组函数依赖所涉及的属性全体为 \(U_i\)
- 令 \(F_i\) 为 \(F_{min}\)在 \(U_i\)上的投影
- 则 \(\rho=\{R_1(U_1,F_1),\cdots,R_k(U_k,F_k)\}\) 是 \(R(U,F)\) 的一个保持函数依赖的分解
- 并且每个 \(R_i(U_i,F_i)\in 3NF\)
例子
- \(U=\{A,B,C,D,E\},F=\{A\to B,B\to C,AD\to E\}\)
- 分组
- \(\{(AB),A\to B\}\)
- \(\{(BC),B\to C\}\)
- \(\{(ADE),AD\to E\}\)
同时保持函数依赖和无损连接的分解
- \(R(ABC;A\to C, B\to C)\)
- 按保持无损连接分解,码为 \(AB\)
- 分解为 \(\{AC;A\to C\},\{AB\}\)
- 丢失了函数依赖 \(B\to C\)
- 按保持函数依赖分解
- 进行分组 \(\{AC;A\to C\},\{BC;B\to C\}\)
- 分解是有损的
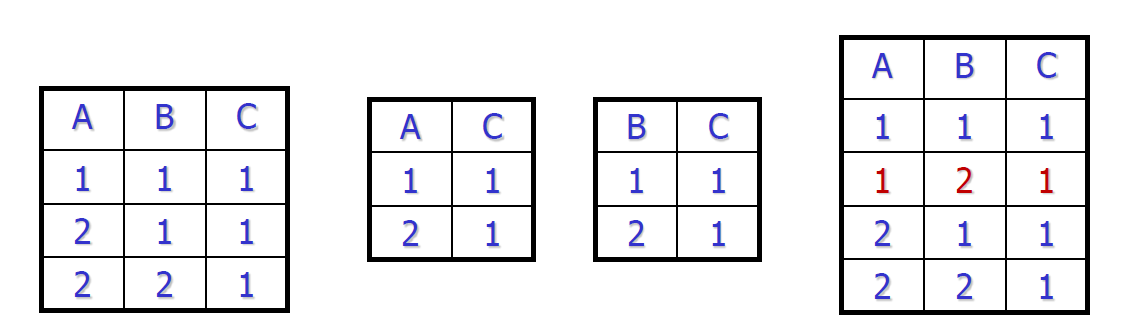
- 如何在保持函数依赖的同时,进行无损分解?
- 从重构的表中删除不在原来表里的行
- 怎么删除?和原来的表的码做一次连接
- 上述分解为 \(\{AC;A\to C\},\{BC;B\to C\},\{AB\}\)
分解算法
- 设 \(\rho=\{R_1(U_1,F_1),\cdots,R_k(U_k,F_k)\}\) 是 \(R(U,F)\) 的一个保持函数依赖的 3NF 分解
- 设 \(X\) 是 \(R(U,F)\) 的码,若有某个 \(U_i,X\subseteq U_i\) 则 \(\rho\) 即为所求
- 否则结果为 \(\rho\cup \{R^\ast(X,F_X)\}\)
其他
其他分解方式
- 先将所有的关系模式打散,然后合并
- \(R_1(AB;\{A\to B\})\)
- \(R_2(AC;\{A\to C\})\)
- \(R_3(AD; \{A\to D\})\)
- 合并为 \(R(ABCD;A\to B,A\to C;A\to D)\)
悬挂元组
- 泛关系
- \(R\) 分解为 \(R_1,\cdots,R_n\) ,则 \(r_1\bowtie r_2\bowtie\cdots\bowtie r_n\) 称为泛关系
- 在 \(r_i\) 中出现,但在 \(\prod_{R_i}(r_1\bowtie r_2\bowtie\cdots\bowtie r_n)\) 中没有出现的元组,称为悬挂元组
- 悬挂元组代表了不完整信息
- 模式分解允许一些不完整信息在数据库中的记录
模式调优
- 规范化为了消除异常,模式调优是追求性能
- \(R(XYZ)\) 还是 \(R_1(XY)\) 和 \(R_2(XZ)\)
- 一般情况下 \(R\) 好于 \(R_1\) 和 \(R_2\),在下面情况下后者较好:
- 大多数用户的存取分别在两个集合上
- \(Y\) 经常访问,但是 \(Z\) 很少访问
- 属性 \(Y\) 和 \(Z\) 的值占用很大空间
- 大多数用户的存取分别在两个集合上
- 一般情况下 \(R\) 好于 \(R_1\) 和 \(R_2\),在下面情况下后者较好:
冗余列
- 把一个表里的某一列,复制到另一个表中
- 反规范化的设计
- 冗余列的好处:避免表连接
- 模式1
- Order1(supplier_ID,part_ID,quantity,supplier_address)
- Supplier(supplier_ID,supplier_name,supplier_address)
- 模式2
- Order2(supplier_ID,part_ID,quantity)
- Supplier(supplier_ID,supplier_name,supplier_address)
- 冗余列可以减少复杂查询中的表连接操作
- 模式 1 有利于经常查询供应某种零件的供应商地址
- 模式 2 有利于新订单的插入
星形模式
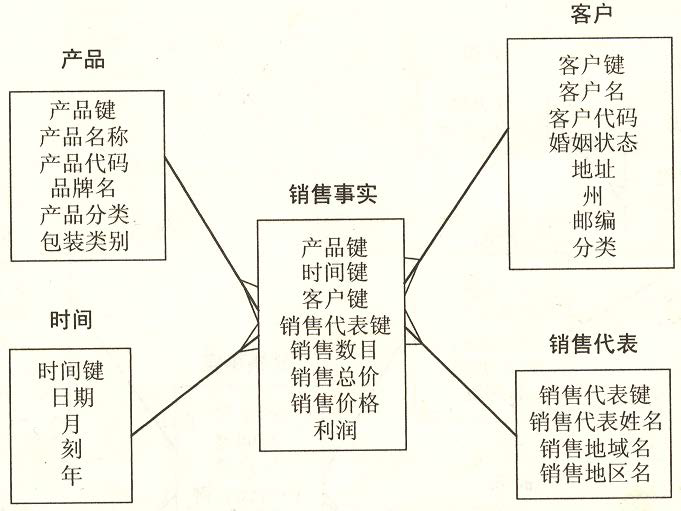
- 对于每个产品而言,产品分类是有冗余的
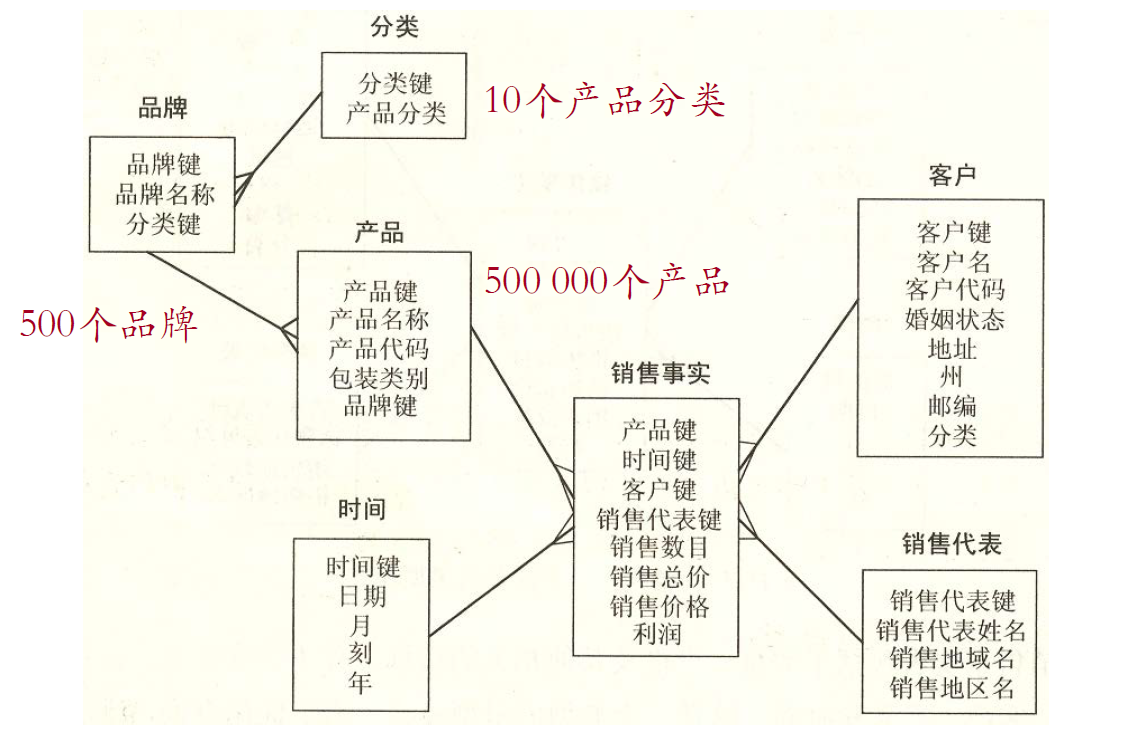
雪花模式:星形模式的规范化
- 不是好的设计
- 虽然没有冗余,但是如果需要看某个类别的销售情况,需要通过好几步才能实现,不直观,速度慢
冗余与分解
- 分解通常使得对复杂查询的回答的效率更差,因为在查询求值期间必须执行额外的连接
- 分解使得对简单查询的回答更有效,因为这种查询通常涉及相同关系的一小部分属性
- 分解通常使得简单的更新事务更有效
- 分解能降低存储空间的要求,因为它一般能消除冗余数据
- 如果冗余级别低,则分解会增加存储的需求
垂直划分
- 将经常同时访问的属性放在同一个表里
- 对每个查询,我们统计不同属性之间被同时访问的次数
- 事务-属性交叉矩阵

- 统计结果
- 属性关联矩阵
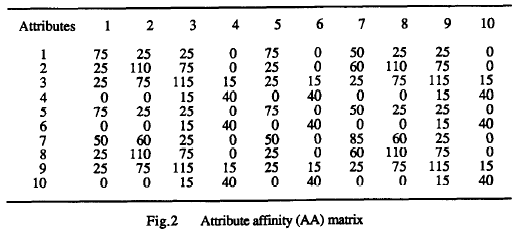
- 属性带权关联图
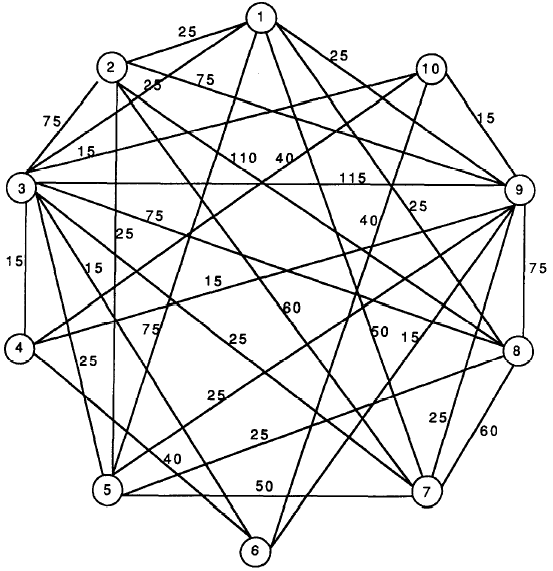
- 图分割