数据库概论.陈立军.05.关系规范化(2)
关系规范化
- 如何判断关系模式的范式级别?
- 看看其他属性有无对候选码的不良依赖
- 如何求关系模式的候选码?
- 一般化这个问题
- 给定一组函数依赖,是否能导出另外一些函数依赖,或另外的函数依赖是否成立?
逻辑蕴涵
逻辑蕴含定义
- 关系模式 \(R(U,F)\) ,\(F\) 是其函数依赖集,\(X,Y\subseteq U\),如果从 \(F\) 的函数依赖能够推出 \(X\to Y\),则称 \(F\) 逻辑蕴涵 \(X\to Y\) ,记作 \(F\vdash X\to Y\)
- 直观上的理解,\(X\to Y\) 能通过 \(F\) 的函数依赖推导出来
闭包
- 被 \(F\) 所逻辑蕴涵的函数依赖的全体所构成的集合称作 \(F\) 的闭包,记作 \(F^+=\left\{X\to Y|F\vdash X\to Y\right\}\)
- 一个例子
\[ R(X,Y),F=\{X\to Y\} \]
\[ \begin{aligned} F^+=&\{\\ &X\to\Phi,X\to X,X\to Y,X\to XY\\ &Y\to\Phi,Y\to Y\\ &XY\to\Phi,XY\to X,XY\to Y,XY\to XY\\ &\} \end{aligned} \]
- 规模是指数级的
Armstrong 公理系统
- 自反律(reflexivity)
- 若 \(Y\subseteq X\) ,则 \(X\to Y\)
- 增广律(augmentation)
- 若 \(X\to Y\),则 \(XZ\to YZ\)
- 传递律(transitivity)
- 若 \(X\to Y,Y\to Z\) 则 \(X\to Z\)
应用
- 上面的例子
- \(X\to XY\):增广律
- \(X\to Y\Rightarrow XX\to XY\Leftrightarrow X\to XY\)
正确性及完备性
- \(A=\{\;f\;|\;用\;\mathrm{Armstrong}\;公理从\;F\;中导出的函数依赖\;f\;\}\)
- \(B=\{\;f\;|\;被\;F\;所逻辑蕴涵的函数依赖\;f\;\}\)
- 完备性
- \(B\subseteq A\)
- \(F\) 所蕴涵的函数依赖都能用 Armstrong 公理从 \(F\) 中导出
- 正确性
- \(A\subseteq B\)
- 用 Armstrong 公理从 \(F\) 中导出的函数依赖必为 \(F\) 所蕴涵
Armstrong 公理正确性证明
自反律
- 设 \(r\) 是 \(R<U, F>\)上的任一关系,\(t,s\in r\)
\[ \begin{aligned} &t[X]=s[X],Y\subseteq X\\ \Rightarrow\;&t[Y]=s[Y]\\ \Rightarrow\;&X\to Y\\ \end{aligned} \]
- 函数依赖 \(X\to Y\) 的定义
- \(t[X]=s[X]\Rightarrow t[Y]=s[Y]\)
增广律
\[ \begin{aligned} &t[XZ]=s[XZ],X\to Y\\ &\\ &t[XZ]=s[XZ],X\to Y\\ \Rightarrow\;&t[X]=s[X]\\ \Rightarrow\;&t[Y]=s[Y]\\ &\\ &t[XZ]=s[XZ]\\ \Rightarrow\;&t[Z]=s[Z]\\ &\\ &t[Z]=s[Z],t[Y]=s[Y]\\ \Rightarrow\;&t[YZ]=s[YZ]\\ \Rightarrow\;&XZ\to YZ\\ \end{aligned} \]
传递律
\[ \begin{aligned} &t[X]=s[X],X\to Y,Y\to Z\\ &\\ &t[X]=s[X],X\to Y\\ \Rightarrow\;&t[Y]=s[Y]\\ &\\ &t[Y]=s[Y],Y\to Z\\ \Rightarrow\;&t[Z]=s[Z]\\ \Rightarrow\;&X\to Z\\ \end{aligned} \]
导出的其他定理
- 合并律(union rule)
- 若 \(X\to Y,X\to Z\) ,则 \(X\to YZ\)
- 分解律(decomposition rule)
- 若 \(X\to YZ\) ,则 \(X\to Y,X\to Z\)
- 伪传递律(pseudotransitivity rule)
- 若 \(X\to Y,WY\to Z\) 则 \(WX\to Z\)
合并律
\[ \begin{aligned} &X\to Y,Y\to Z\\ &\\ &X\to Y\\ \Rightarrow\;&X\to XY\\ &\\ &X\to Z\\ \Rightarrow\;&XY\to YZ\\ &\\ &X\to XY,XY\to YZ\\ \Rightarrow\;&X\to YZ\\ \end{aligned} \]
分解律
\[ \begin{aligned} &X\to YZ\\ &\\ &Z\subseteq YZ\\ \Rightarrow\;&YZ\to Z\\ &\\ &X\to YZ,YZ\to Z\\ \Rightarrow\;&X\to Z\\ &\\ &同理,X\to Y\\ \end{aligned} \]
伪传递律
\[ \begin{aligned} &X\to Y,WY\to Z\\ &\\ &X\to Y\\ \Rightarrow\;&XW\to WY\\ &\\ &XW\to WY,WY\to Z\\ \Rightarrow\;&XW\to Z\\ \end{aligned} \]
公理应用示例
- 已知
- \(R< U, F >\)
- \(U = (A, B, C, G, H, I)\)
- \(F = \{A\to B, A\to C, CG\to H, CG\to I, B→H\}\)
- 问如下函数依赖是否成立
- \(A\to H\) 成立
- \(CG\to HI\) 成立
- \(AG\to I\) 成立
属性集的闭包
- 将之前的一个证明的问题转化为计算的一个问题
定义
- 设 \(F\) 为属性集 \(U\) 上的一组函数依赖,\(X\subseteq U\)
- \(X_F^+=\{A|X\to A\;能由\;F\;根据\;\mathrm{Armstrong}\;公理导出\}\)
- 称 \(X_F^+\) 为属性集 \(X\) 关于函数依赖集 \(F\) 的闭包
例子
- \(U=\{A,B,C\}\)
- \(F=\{A\to B,B\to C\}\)
- 则属性集的闭包如下
- \(A_F^+=ABC\)
- \(B_F^+=BC\)
- \(C_F^+=C\)
求解属性集闭包的通用算法
- 输入:\(X, F\)
- 输出:\(X_F^+\)
- 初始化为本身:\(X_F^+:=X\)
\[ \begin{aligned} &\mathrm{while}\;(X_F^+发生变化)\;\mathrm{do}\\ &\quad \mathrm{for\;each}\;函数依赖\;A\to B\;\mathrm{in}\;\mathrm{do}\\ &\qquad \mathrm{begin}\\ &\qquad \quad \mathrm{if}\;A\subseteq X_F^+\;\mathrm{then}\;X_F^+:=X_F^+\cup B\\ &\qquad \mathrm{end}\\ \end{aligned} \]
算法正确性
\[ \begin{aligned} &A\subseteq X_F^+\Rightarrow X\to A\\ &X\to A,A\to B\Rightarrow X\to B\\ \end{aligned} \]
算法会终止
- 最多 \(|U-X|\) 步
算法示例
- \(U = (A, B, C, G, H, I)\)
- \(F = \{A\to B, A\to C, CG\to H, CG\to I, B\to H\}\)
- 计算 \((AG)_F^+\)
- 算法流程
- \((AG)_F^+=AG\)
- \((AG)_F^+=ABCGHI\)
- 算法效率并不是很高
- 提高效率可以将函数依赖进行排列
闭包的封闭性
- \((X^+)^+=X^+\)
证明
- 证明他们互相包含
- \((X^+)^+\supseteq X^+\) 显然
- \((X^+)^+\subseteq X^+\)
- \(\forall A\in(X^+)^+\Rightarrow X^+\to A\)
- \(X^+\to A,X\to X^+\Rightarrow X\to A\Rightarrow A\in X^+\)
- 由任意性,\((X^+)^+\subseteq X^+\)
封闭的
- 如果 \(X^+=X\),则称 \(X\) 是封闭的
例题
- \(R(ABCD)\) 的封闭属性集只有 \(\Phi\) 和 \(\{ABCD\}\),求 \(R\) 的函数依赖集
- 每一个码都是候选码
- \(A\to B,B\to C,C\to D, D\to A\)
- \(R(ABCD)\) 的封闭属性集只有 \(\Phi,\{AB\},\{ABCD\}\),求 \(R\) 的函数依赖集
- \(A\to B,B\to A,C\to D,D\to C,C\to A\)
闭包与函数依赖证明之间的关系
- 有没有一般性的算法判定 \(X\to Y\) 是否能由 \(F\) 根据 Armstrong 公理导出?
- 如果计算出 \(F^+\),再判断 \(X\to Y\) 是否属于 \(F^+\),则由于 \(F^+\) 的计算非常复杂,实际上是不可行的
- 通过属性集的闭包计算
- \(X\to Y\) 能由 Armstrong 公理导出 \(\Leftrightarrow\) \(Y\subseteq X_F^+\)
- 从几何证明到代数计算
Armstrong 公理完备性证明
- 反证法
- 假定存在函数依赖 \(X\to Y\) 被 \(F\) 逻辑蕴涵,但 \(X\to Y\) 不能用 Armstrong 公理从 \(F\) 中导出,则存在 \(Y\) 的子集不属于 \(X\) 的闭包,也即:\(Y\not\subseteq X_F^+,Y-X^+_F\ne\Phi,U-X_F^+\ne\Phi\)
- 构造 \(R(U)\) 上的关系 \(r\) 如下:
| \(r\) | \(X_F^+\) | \(U-X_F^+\) |
|---|---|---|
| \(t\) | 1 | 0 |
| \(s\) | 1 | 1 |
- 下面证明,由于 (1)(2) 本身是矛盾的,推出假设不成立
- \(r\) 满足 \(F\)
- \(r\) 不满足 \(X\to Y\)
- \(r\) 满足 \(F\)
- 设 \(W\to V\) 是 \(F\) 的任意一个函数依赖,由下述推导得到 \(r\) 满足 \(W\to V\)(\(t[W]=s[W]\Rightarrow t[V]=s[V]\))
- 即 \(r\) 是 \(R(U,F)\) 上的关系
\[ \begin{aligned} t[W]=s[W]&\Rightarrow W\subseteq X_F^+(构造决定,看关系\;r)\\ &\Rightarrow X\to W\\ X\to W,W\to V&\Rightarrow X\to V\\ &\Rightarrow V\subseteq X_F^+\\ &\Rightarrow t[V]=s[V]\\ \end{aligned} \]
- \(r\) 不满足 \(X\to Y\)
- \(Y-X^+_F\ne\Phi\)
- 故 \(Y\) 中存在一个属性 \(A\notin X_F^+\)
- 在 \(r\) 中有 \(t[X]=s[X]\) ,而 \(t[A]≠s[A]\)
- 所以 \(t[Y]\ne s[Y]\),即 \(X\to Y\) 不成立
候选码的计算
- NP 的
- 我们期望通过一些约束条件,限制搜索范围
属性集的派性
- 左部属性,只出现在 \(F\) 左边的属性
- 右部属性,只出现在 \(F\) 右边的属性
- 双部属性,出现在 \(F\) 两边的属性
- 外部属性,不出现在 \(F\) 中的属性
不同派性的性质
- 左部属性一定出现在任何候选码中
- 右部属性一定不出现在任何候选码中
- 外部属性一定出现在任何候选码中
做题的 trick
- 出现在左边的属性加上划线,出现在右边的属性加下划线
候选码的计算
- 先求出左部属性和外部属性,再求属性集闭包
- 如果闭包已经是属性集全集,说明左部属性已经是候选码(唯一的候选码)
- 否则则需要和双部属性组合
例子1
- \(U=\{C,T,H,R,S\}\)
- \(F=\{C\to T,HR\to C,HT\to R,HS\to R\}\)
- 左部属性+外部属性:\(HS\)
- \((HS)_F^+=HSRCT\)
- 候选码唯一:\(HS\)
- 主属性 \(HS\),非主属性 \(CTR\)
- 是 \(2NF\):没有部分依赖(求出 \(H_F^+,S_F^+\))
- 不是 \(3NF\):\(HS\to C,C\to T\)
例子2
- \(U = \{A,B,C,D,E\}\)
- \(F = \{AE\to C,AC\to D,CD\to B,D\to E\}\)
- 左部属性+外部属性:\(A\)
- 双部属性:\(C,E,D\)
- \(A_F^+=A\) 不是候选码
- 和双部属性组合
- \((AC)_F^+=ACDBE\) 是候选码
- \((AD)_F^+=ADECB\) 是候选码
- \((AE)_F^+=AECDB\) 是候选码
- 主属性 \(ACDE\),非主属性 \(B\)
- 是 \(2NF\)
- 不是 \(3NF\)
- \(AC\to CD, CD\to B\)
求一个候选码的一般算法
- 输入:关系模式 \(<U, F>\)
- 输出:一个候选码 \(K\)
- 思路:每次删除一个属性,看它的闭包是否还是整个属性集
\[ \begin{aligned} &\mathrm{Key-Finding}(U, F)\\ &\mathrm{Begin}\\ &\quad(1)\;K:= U\\ &\quad(2)\;构造一个\;FD: K\to T,其中\;T\notin U\\ &\quad(3)\;\mathrm{for}\;每一个属性\;A\in K\;\mathrm{do}\\ &\quad\qquad\mathrm{if\;Membership}(F\cup\{K\to T\},(K-A)\to T)\\ &\quad\qquad\mathrm{then}\;K:= K-A\\ &\quad\mathrm{return}(K)\\ &\mathrm{end}\\ \end{aligned} \]
- \(\mathrm{Membership}(F, X\to Y)\): 判断 \(X\to Y \in F^+\)
- 上面算法为什么要这么构造?
- \(K-A\) 是候选码 \(\Leftrightarrow\) \((K-A)_F^+=U\) \(\Leftrightarrow\) \((K-A)\to K \in F^+\)
求全部候选码的算法:替换法
- 输入:关系模式 \(R<U,F>\)
- 输出:\(R<U,F>\) 的全部候选码 \(W\)
- 思路
- 先找到一个候选码,这个候选码包括左部属性和双部属性(不考虑外部属性,考虑的话将其当作左部属性即可)
- 用其他的双部属性替代候选码中得到双部属性
\[ \begin{aligned} &\mathrm{begin}\\ &(1)\;K:=\mathrm{Key-Finding}(U,F)\\ &(2)\;K\;入队列\;Q\\ &(3)\;\mathrm{while}\;队列\;Q\ne\Phi\;\mathrm{do}\\ &\qquad\quad K:=队列\;Q\;的头\\ &\qquad\quad W:=W\cup\{K\}\\ &\qquad\quad D:=K\;中全部双部属性\\ &\qquad\quad\mathrm{while}\;D\ne\Phi\;\mathrm{do}\\ &\qquad\qquad A:=D\;中一个双部属性\\ &\qquad\qquad D:=D-\{A\}\\ &\qquad\qquad\mathrm{for}\;每一个\;X\to Y\in F\;\mathrm{do}\\ &\qquad\qquad\quad \mathrm{if}\;A\in Y\;\mathrm{then}\;K’:=(K-A)\cup\{X\}\\ &\qquad\qquad\quad\mathrm{if}\;K’\notin Q\;\mathrm{then}\;K’\;入队列\;Q\\ &\mathrm{end}\\ \end{aligned} \]
求全部候选码的算法示例
- \(U=\{A, B, C, D, E, G\}\)
- \(F=\{AB\to C, C\to A, C\to B, AD\to B, BE\to G, G\to A\}\)
- 所有候选码 = \(\{EDC, EDA, EDG, EDB\}\)
函数依赖集的等价性
- 目的:利用等价性找到一个简化的函数依赖集
- 函数依赖越少,检查起来越简单
等价性的定义(闭包相同)
- 对于函数依赖集 \(F,G\) ,若 \(F^+=G^+\),则称 \(F\) 与 \(G\) 等价
如何判定两个函数依赖集等价
- \(F^+=G^+\Leftrightarrow F\subseteq G^+,G\subseteq F^+\)
- 证明起来还是挺复杂的
函数依赖集的最小覆盖
- 函数依赖集 \(F\) 的最小覆盖 \(F_{min}\)
- 单属性化:对于 \(F\) 中任一函数依赖 \(X\to A\), \(A\) 必是单属性
- 无冗余化:\(F\) 中不存在这样的函数依赖 \(X\to A\),使得 \(F\) 与 \(F−\{X\to A\}\) 等价
- 既约化:\(F\)
中不存在这样的函数依赖 \(X\to A\), 在
\(X\) 中有真子集 \(Z\), 使得 \(F\) 与 \((F−\{X\to A\})\cup\{Z\to A\}\) 等价
- 消除冗余属性
求解函数依赖集的最小覆盖
单属性化
- 逐个检查 \(F\) 中各函数依赖 \(F_i:X\to Y\)
- 若 \(Y=A_1A_2\cdots A_k,k\ge2\),则用诸 \(X\to A_i\) 代替 \(Y\)
无冗余化
- 逐个检查 \(F\) 中各函数依赖 \(X\to A\)
- 令 \(G=F-\{X\to A\}\),若 \(A\in X_G^+\),则从 \(F\) 中去掉该函数依赖
既约化
- 逐个检查 \(F\) 中各函数依赖 \(X\to A\)
- 设 \(X=B_1\cdots B_m\),逐个考查 \(B_i\)
- 若 \(A\in(X-B_i)_F^+\),则以 \(X−B_i\) 取代 \(X\)
求最小覆盖例子
无冗余化
- \(F=\{A\to B,B\to A,A\to C,B\to C\}\),求 \(F_{min}\)
- \(F_{min}=\{A\to B,B\to A,A\to C\}\)
- \(F_{min}=\{A\to B,B\to A,B\to C\}\)
既约化
- \(F=\{C\to A,A\to G ,CG\to B,B\to A\}\),求 \(F_{min}\)
- \(F\) 是无冗余的
- \(F_{min}=\{C\to A,A\to G ,C\to B,B\to
A\}\)
- 还得进一步无冗余化
- \(F_{min}=\{A\to G ,C\to B,B\to A\}\)
顺序
- 先既约化,再无冗余化
函数依赖和多值依赖的推理规则

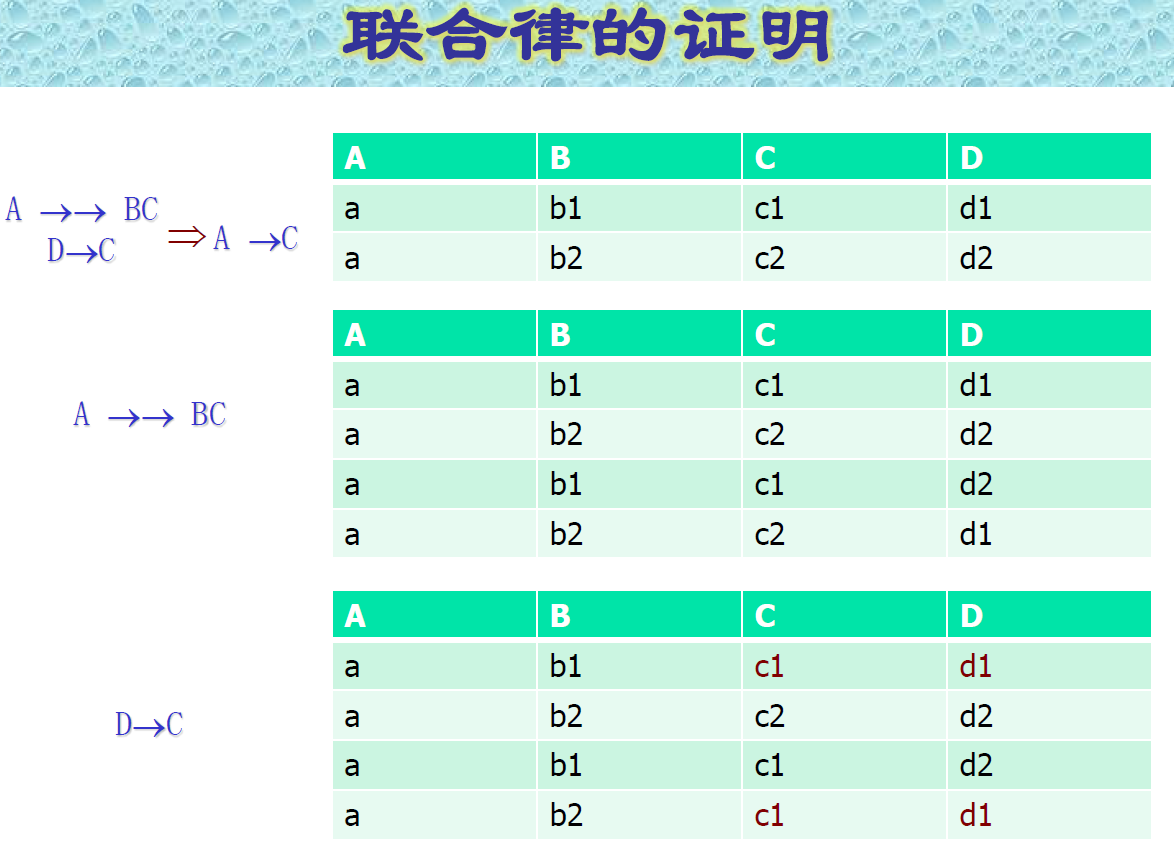
联合律的证明
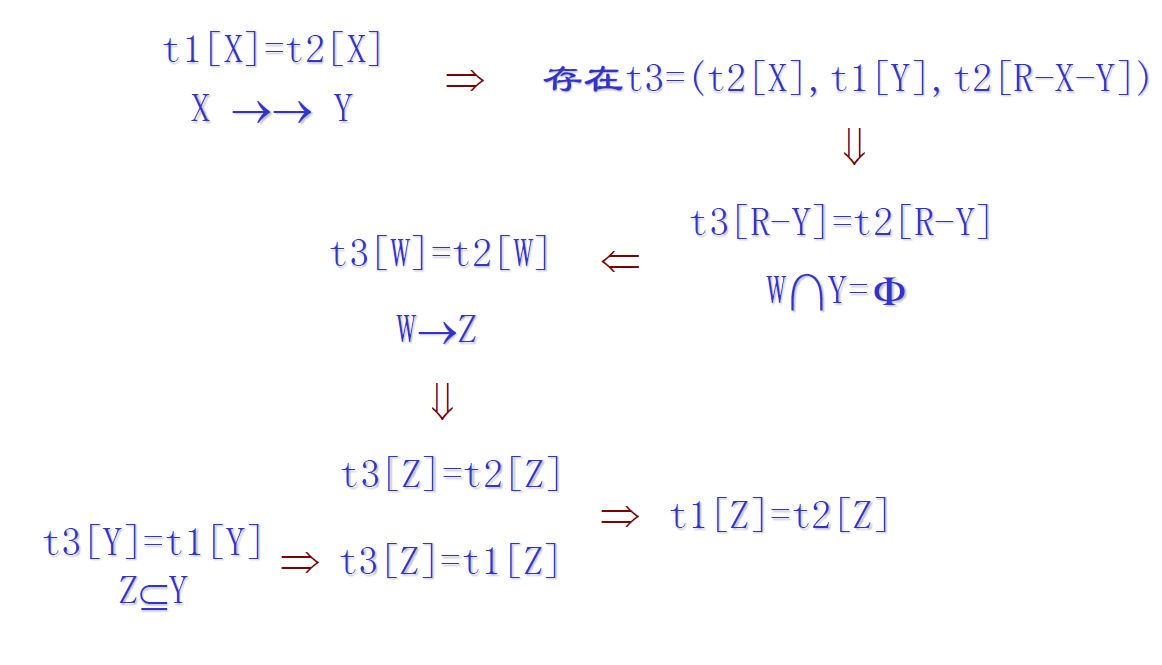
- 填表的方式证明