GAMES202.闫令琪.10.基于物理的材质(微表面模型)

Posted on 2021-05-12 Edited on 2021-06-10 In CG.GAMES202 Views:

基于物理的材质、微表面模型、NDF、G 项、多次反射的补充

https://www.bilibili.com/video/BV1YK4y1T7yY

基于物理的材质

PBR vs PBR Material

PBR：Physically-Based Rendering（基于物理的渲染）
- 所有在渲染中涉及到的东西都必须是物理的
- 材质、光照、相机、光线传播等
  - material、light、camera、light transport
  - 透镜、透镜组
- PBR 不仅限于材质，但是实时渲染领域通常就是指材质
实时渲染材质的落后于离线渲染
- 丰富程度
  - 实时渲染用的材质一般都是研究的比较透彻的，能够比较快的渲染
- 准确度（质量）
  - 为了速度，牺牲质量
  - 头发的渲染
  - 实时渲染是在保证速度的前提下提高质量
- ”PB“ 在实时渲染中并没有那么物理
  - 做了大量的简化

实时渲染中的 PBR

主要有两类：surface、volume
在表面上定义的、在体积上定义的

surface

在物体表面上定义的
microfacet models
- 实际于物理的描述
- 但有时候不正确的使用，则不是 PBR
disney principled BRDFS：基于 Disney 的原则设计的 BRDF
- 发明的时候希望被用于离线渲染，但同时也能被用在实时渲染之中
- 轻量级的计算，实现简单
- 能够表示材质种类很多，效果也非常不错
- 不是 PBR 的
- artist friendly：为了艺术家使用方便而设计的
- 总体而言描述的还是挺好的，但是在细节上还是不完美
- 一张效果图：左（照片）、右（渲染图）
  - 渲染器：Hyperion
  - 最早的 Disney 工作室所在的街的名字

volume

在体积上定义的
- 更加困难
mostly focused on fast and approximate single scattering and multiple scattering
cloud, hair, skin, etc
- 烟雾、云、皮肤、头发

实时渲染

实时渲染中材质并没有很多其他的新理论
但是会有很多实现上的 hacks
- 为了降低开销
速度是前提
- speed、performance

Microfacet BRDF

微表面模型
GAMES101 中有所介绍
微表面的 BRDF：微观
- 微表面的法线各不相同
- 这些法线的不同分布造成最终渲染结果的不同

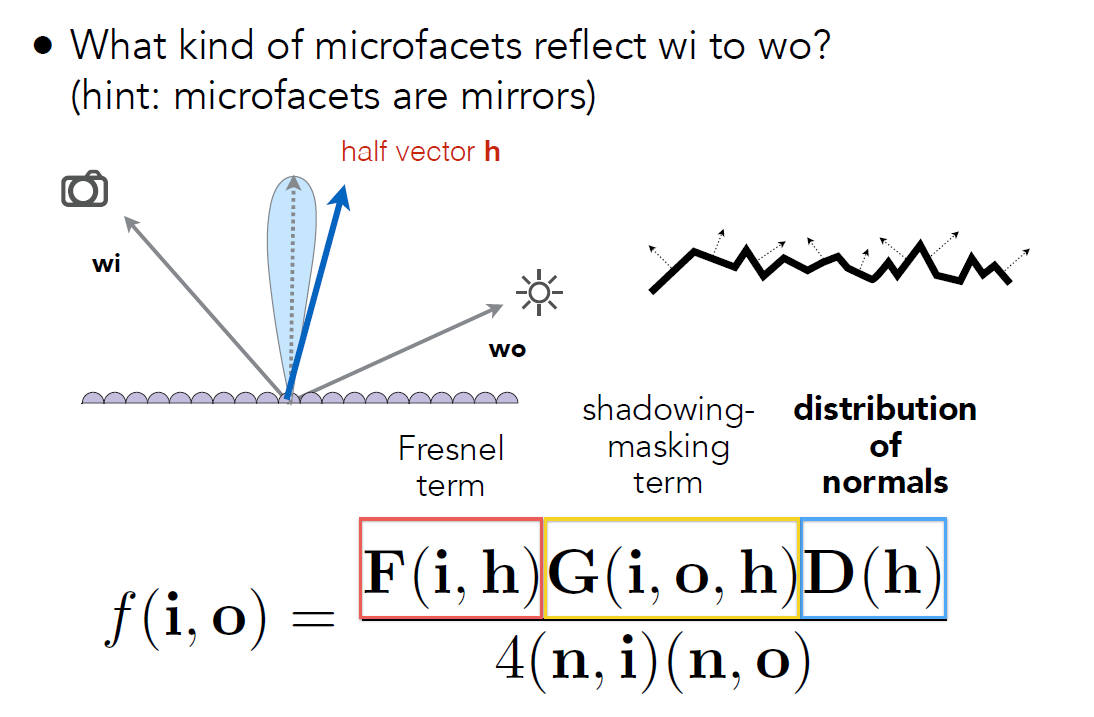
F 项：菲涅尔项，从一个角度看过去有多少能量会被反射
G 项：shadowing masking
D 项：微表面的法线分布
- 半程向量和微表面的法线一致的情况下，才能把光线从入射方向反射到出射方向去

菲涅尔项

The Fresnel Term
反射的能量和入射角的方向有关

绝缘体（Dieletric）、导体（Conduct）的性质不太一样
- GAMES101
Schlick's approximation

\[ R(\theta) =R_{0}+\left(1-R_{0}\right)(1-\cos \theta)^{5} \]

\[ R_{0} =\left(\frac{n_{1}-n_{2}}{n_{1}+n_{2}}\right)^{2} \]

NDF

Normal Distribution Function
微表面的法线分布函数

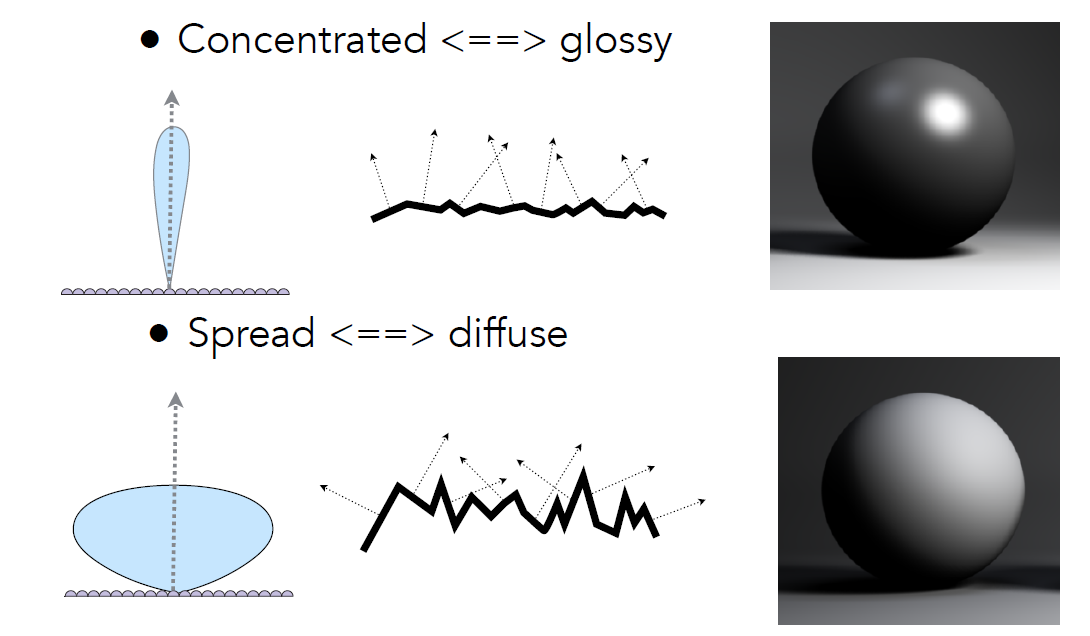
分布比较集中：glossy -> specular
分布比较散乱：diffuse
怎么让微表面在不同材质之间变化
- 高度场上下做一个拉伸（scale）
- 上下做一个拉伸之后
  - 可以让法线的分布不再集中，从 glossy 转变为 diffuse
  - 相当于把所有面变得倾斜过来了
  - 微表面之间形成的沟壑变得越来越深，形成粗糙的表面
NDF：微表面的法线分布函数
- 二维
有很多描述 NDF 的模型
- Beckmann, GGX, etc
- Detailed models [Yan 2014, 2016, 2018, …]
  - 实时渲染中用的比较少，代价太大
怎么把一个 2D 的分布函数可视化在一个平面上？
- 法线，半球面的分布（不能向下）
- 从上往下拍扁即可，projected solid angle

Beckmann NDF

\[ D(h)=\dfrac{e^{-\dfrac{\tan^2\theta_h}{\alpha^2}}}{\pi\alpha^2\cos^4\theta_h} \]

和高斯函数很像
高斯函数
- 高斯函数是对正态函数的一个更通用的抽象
- 表示一类中间高，往两边衰减的函数分布
\(\alpha\)：一个参数，描述粗糙程度（正态函数中的方差 \(\sigma\) ）
- \(\alpha\) 越小，越趋向于镜面 specular
\(\theta_h\)：法线（镜面：垂直表面）和半程向量所成的夹角
各向同性的，不涉及 \(\phi\)
- 复杂的 Beckmann NDF 是可以描述各向异性的材质的
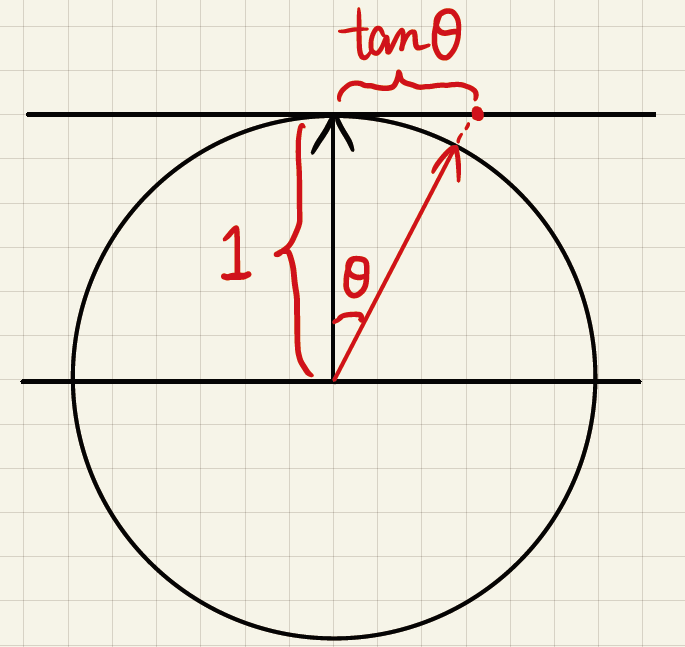
为什么分子中是 \(\tan^2\theta_h\) 而不是 \(\theta^2_h\) ？
- Beckmann NDF 是定义在坡度空间上的（slope space）
- 高斯函数本身的定义域是无限大的，定义在 \(\tan\theta_h\) 上可以满足当 \(\theta_h\) 取遍 \([0,\dfrac{\pi}{2}]\)，满足这个无限大的条件
- 保证了不会有微表面的法线是朝下的

分母项
- 归一化项
- 让 NDF 在 projected solid angle 上积分为 1

GGX NDF

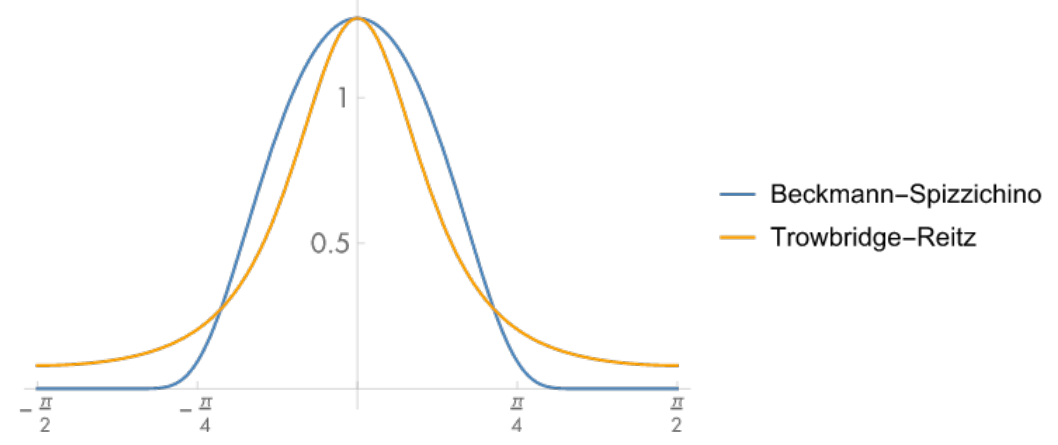
GGX (or Trowbridge-Reitz) [Walter et al. 2007]
TR 模型
特点：长尾的（long tail）
GGX 会很快衰减没但是衰减到一定程度之后，速度会变慢，导致长尾
- grazing angle 还不会是 0

GGX 能够看到周围的光晕现象
- GGX 的效果更加自然

Extending GGX

Extending GGX [by Brent Burley from WDAS]
Walt Disney Animation Studios
迪士尼动画工作室
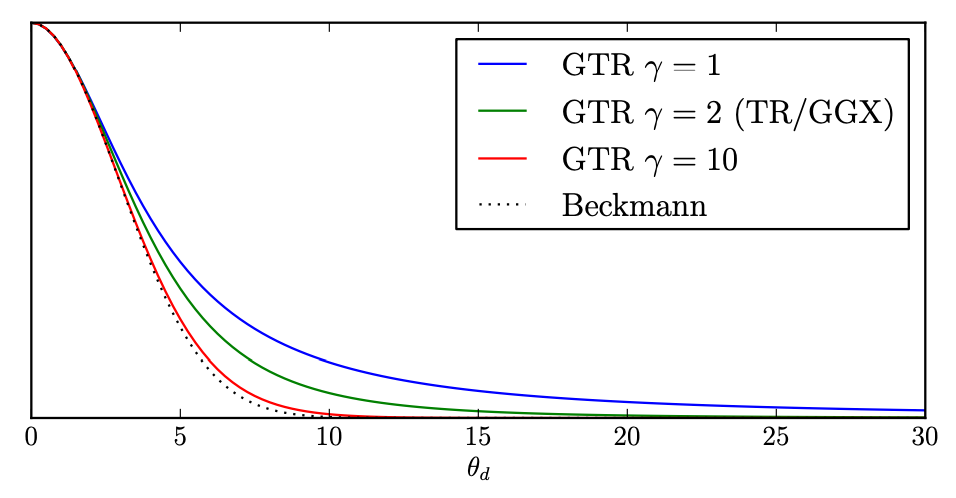
GTR (Generalized Trowbridge-Reitz)
Even longer tails
定义了一个参数 \(\gamma\)，当 \(\gamma=2\) 的时候，就是 GGX
- 当 \(\gamma\) 取的比较大的时候，会接近于 Backmann 的效果（有趣）

Shadowing-Masking

几何项 G
微表面之间的互相遮挡问题
- 尤其是在 grazing angle 的时候
入射光、反射光都可能被遮挡

Shadowing：light（左）
Masking：eye（右）
体现由于遮挡导致的变暗的现象
基本性质
- 靠近 grazing angle 的时候，接近于 0
- 接近法线的时候，接近于 1

G term 的重要性

\[ f(\mathbf{i}, \mathbf{o})=\frac{\mathbf{F}(\mathbf{i}, \mathbf{h}) \mathbf{G}(\mathbf{i}, \mathbf{o}, \mathbf{h}) \mathbf{D}(\mathbf{h})}{4(\mathbf{n}, \mathbf{i})(\mathbf{n}, \mathbf{o})} \]

如果不考虑 G 项
- 在边缘的地方，分母 \(n\cdot i\) 接近于 0
- 导致结果巨大，渲染的结果就是边缘有白色的亮圈
- 这是不符合物理规律的

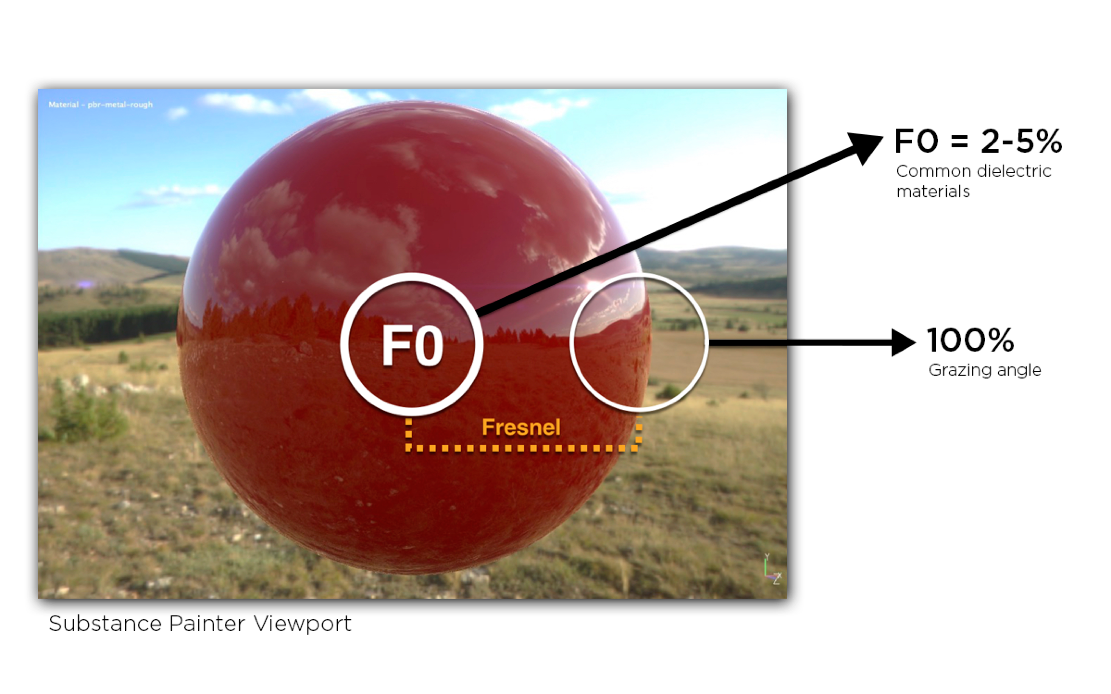
The Smith shadowing-masking term

一个常用的 shadowing-masking 项
理论非常复杂
在具体的发现分布之下推导出一个 G 项
把 shadowing 和 masking 拆开考虑
- 但实际上是有关的
- \(m\) 是半程向量

一个例子

G 项的特征

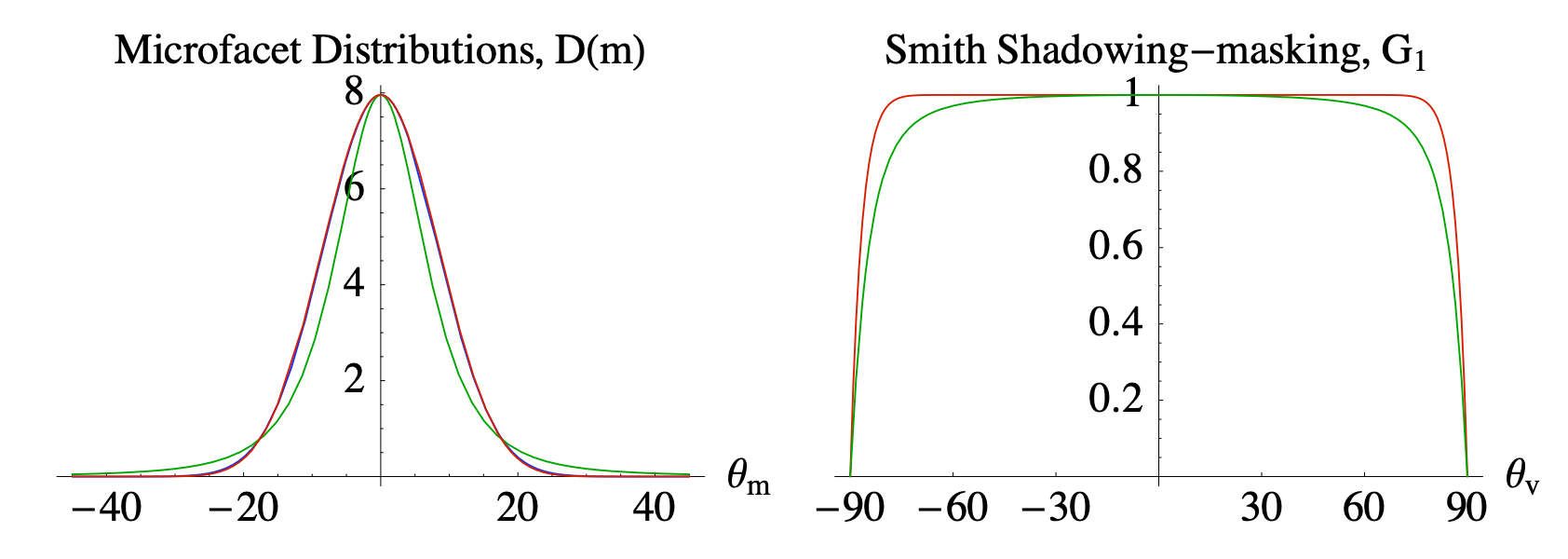
Multiple Bounces

微表面模型还存在一个其他问题：能量损失
该部分链接

roughness 变化
存在的问题，从左到右结果越来越暗了
- 高光到哑光，亮度应该是差不多的

白炉测试

The White Furnace Test

一个实验，空的背景，环境光照各处都是一样的，先保证在 roughness 比较低的情况下，反射出来的颜色和背景一样
随着 roughness 增大，颜色越来越暗，出现能量损失现象

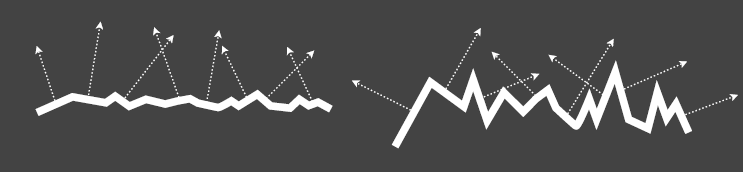
为什么会有能量损失

roughness 越大
- 沟壑越多，光线越容易被挡住
- 多次弹射的光线占比的可能性越大
- 如果我们在使用微表面模型的时候只考虑单次 bounce，损失的能量就越多

解决能量损失的问题

基本思想，把损失的能量补回来
- Heitz et al. 2016
- 准确计算多次 bounce
- 很慢
基本思想
- 如果一束光被遮挡了，说明这一束光发生了下一次的反射

The Kulla-Conty Approximation

一个近似方法
经验性的方式补全丢失的能量
怎么求出丢失的能量？
先算出出射的总能量（这里求解的 BRDF 就是上面考虑了各种项的结果，因此计算出来的结果应该是有损失的）
- 对所有的入射方向的入射光做一个积分
- 我们假设所有方向的入射光 radiance 都是 1，\(L_i=1\)
- 这里的 \(\cos\theta\) 项哪去了？
  - \(\mathrm{d}\omega=\sin\theta\;\mathrm{d}\theta\;\mathrm{d}\phi\)
  - \(\cos\theta\;\mathrm{d}\omega=\sin\theta\;\mathrm{d}\sin\theta\;\mathrm{d}\phi\)

\[ E(\mu_o)=\int_{0}^{2\pi}\int_{0}^{1}f(\mu_o,\mu_i,\phi)\mu_i\;\mathrm{d}\mu_i\;\mathrm{d}\phi \]

\[ \mu=\sin\theta \]

那么损失的能量就是 \(1-E(\mu_o)\)
- 损失的能量和观察方向是相关的
关键思想就是把上面的能量补上

一种设计

补上另外一种 BDRF，使得最终积分的结果为 \(1-E(\mu_o)\)
考虑对称性，我们还有另外一项
- \(c(1-E(\mu_o))(1-E(\mu_i))\)
- \(c\) 为归一化项
我们可以设计其他的积分函数，使得积分结果为 \(1-E(\mu_o)\) 即可
这种设计比较自然

\[ c=f_{ms}(\mu_o,\mu_i)=\dfrac{(1-E(\mu_o))(1-E(\mu_i))}{\pi(1-E_{avg})} \]

\[ E_{avg}=\dfrac{\int_0^1E(\mu)\mu\;\mathrm{d}\mu}{\int_0^1\mu\;\mathrm{d}\mu}=2\int_0^1E(\mu)\mu\;\mathrm{d}\mu \]

验证

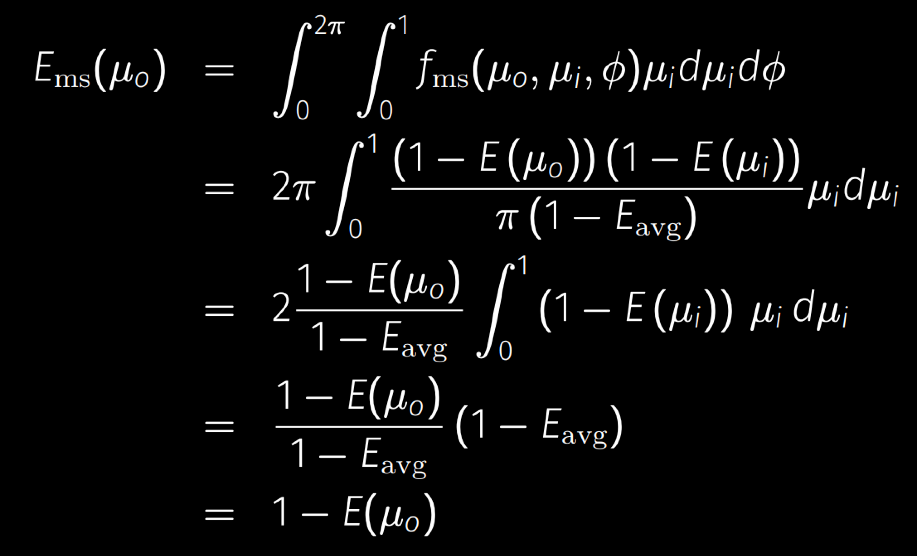
新的问题，怎么计算我们的 \(E_{avg}\)
对于复杂积分的求解
- 预计算、打表
- precompute、tabulate
参数
- \(\mu_o\)
- 具体 BDRF 的参数
  - 简单的 NDF 可以用 roughness
打表

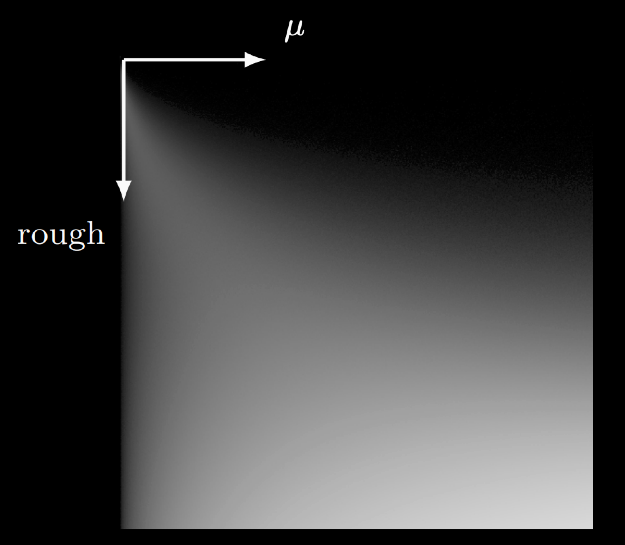
结果

如果 BRDF 有颜色

Color == absorption == energy loss (as it should)
有颜色，表明有吸收，也就是存在能量损失（这些能量的损失是应该损失的，被吸收）
那么就导致原始的积分结果不是 1
我们先考虑没有颜色吸收，按照上面的思路计算出结果，然后再考虑由于颜色吸收导致的能量损失

the average Fresnel

计算一个平均的 Fresnel 项，对不同的入射角进行积分
为什么这么做呢？因为颜色的吸收只会出现在 Fresnel 项中

\[ F_{avg}=\dfrac{\int_0^1F(\mu)\mu\;\mathrm{d}\mu}{\int_0^1\mu\;\mathrm{d}\mu}=2\int_0^1F(\mu)\mu\;\mathrm{d}\mu \]

\(E_{avg}\) 项是不会参与大后续的多次 bounce 中的
- 参与到后续 bounce 中的是 \(1-E(\mu_o)\)

把最终能够看到的能量分类

直接能看到的能量：\(F_{avg}E_{avg}\)
1 次反射之后看到的能量：\(F_{avg}(1-E_{avg})F_{avg}E_{avg}\)
...
\(k\) 次反射之后看到的能量：\(F_{avg}^k(1-E_{avg})^kF_{avg}E_{avg}\)
对上面的能量求和

\[ \dfrac{F_{avg}E_{avg}}{1-F_{avg}(1-E_{avg})} \]

我们将这个系数直接乘到直接计算出来的没有考虑吸收的结果之上即可
- 乘到增加的 BRDF 之上（而不是原来的）
RGB 3 通道是分开计算的

结果

不正确的 Hack

微表面模型比较暗，我们再直接加上一个 diffuse lobe 的结果

问题
- 物理上完全错误
- 不能保证能量守恒
  - 如果加上一个 diffuse lobe 但是能够保证能量守恒，那是正确的