数据库概论.陈立军.05.关系规范化
关系规范化
- 为什么需要关系规范化
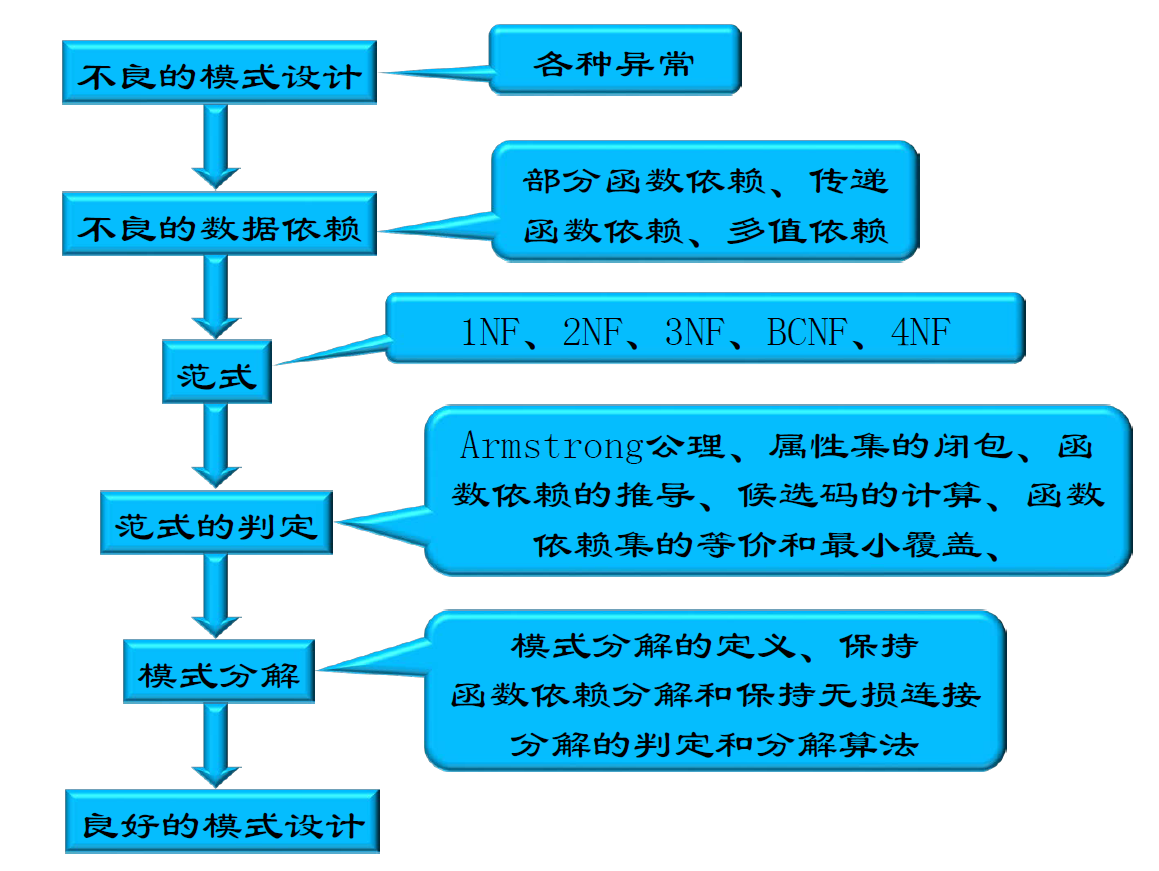
关系模式的设计问题
例子 1
- 为管理职工信息而设计如下一个关系模式
- 问题:当删除职工 A 后,没有等级 4 的员工了,此时如果想再招聘一个等级 4 的员工,不知道如何安排工资
- 不完整了
| 职工 | 级别 | 工资 |
|---|---|---|
| A | 4 | 500 |
| B | 5 | 600 |
| C | 6 | 700 |
| D | 5 | 600 |
| E | 6 | 700 |
- 问题根源:在属性如何取值的问题上,表结构与现实出现偏离
- 现实中
- 职工只和岗位有关系
- 每个级别的工资和职工没关系,只和级别有关系
- 现实中
- 应该这样设计
- 职工 - 级别一张表
- 级别 - 工资一张表
- 问题根源:人为造成了现实当中本来无关属性之间的依赖
异常
- 信息的不可表示问题
- 插入异常:如果没有职工具有 8 级工资,则 8 级工资的工资数额就难以插入
- 删除异常:如果仅有职工 A 具有 4 级工资,删除 A 则会将有关 4 级工资的工资数额信息也一并删除
- 信息的冗余问题
- 数据冗余:职工很多,工资级别有限,每一级别的工资数额反复存储多次
- 更新异常:如果将 5 级工资的工资数额调为 620,则需要找到每个具有 5 级工资的职工,逐一修改
不良的数据依赖
- 解决方案
- 应该这样设计
- 职工 - 级别一张表
- 级别 - 工资一张表
例子 2
- 有些人可能有很多爱好,主码设置为 姓名+爱好
| 姓名 | 年龄 | 性别 | 爱好 |
|---|---|---|---|
| A | 20 | 男 | 电影 |
| A | 20 | 男 | 音乐 |
| B | 18 | 女 | 购物 |
| B | 18 | 女 | 美食 |
| C | 23 | null | null |
- 有些人可能没有爱好,此时它不能插入
- C 的记录是无法插入的(主码非 null )
函数依赖
函数依赖的定义
- 设 \(R(U)\) 是属性集 \(U\) 上的关系模式,\(X,Y\subseteq U\),\(r\) 是 \(R(U)\) 上的任意一个关系
- 如果成立 对 \(\forall t,s\in R\) 若 \(t[X]=s[X]\),则 \(t[Y]=s[Y]\)
- 则称 “\(X\) 函数决定 \(Y\) ” 或 “ \(Y\) 函数依赖于 \(X\) “,记作 \(X\to Y\)
- 称 \(X\) 为决定因素
- 函数依赖的双重否定定义
- 不存在 \(t, s \in r\),\(t[X] = s[X]\),但 \(t[Y]\ne s[Y]\)
- 函数依赖的例子
- 姓名 \(\to\) 学号
例子 1
- 给定如下关系示例,判断如下函数依赖是否成立
| A | B | C | D |
|---|---|---|---|
| a1 | b1 | c1 | d1 |
| a1 | b2 | c1 | d2 |
| a2 | b2 | c2 | d2 |
| a2 | b3 | c2 | d3 |
| a3 | b3 | c2 | d4 |
- \(A\to C\):成立
- 判断在 A 上相等的两行,在 C 上是否相等
- \(C\to A\):不成立
- \(AB\to D\):成立
- \(AB\) 上取值是唯一的
两种依赖的等级
- 满足依赖的关系:依赖在模式的某个关系实例上成立
- 可能在插入几行之后,函数依赖就不成立了
- 模式上成立的依赖:依赖在模式的所有关系实例上都成立
例子2
| A | B | C |
|---|---|---|
| 1 | 2 | 3 |
| 4 | 2 | 3 |
| 5 | 3 | 3 |
- 找出所有可能的函数依赖
- \(A\to B,A\to C,B\to C\)
- \(A\to A,B\to B,C\to C\)
- \(AB\to A,ABC\to A,\cdots\)
- \(\cdots\)
平凡函数依赖
- 如果 \(X\to Y\),\(Y\subseteq X\),则称其为平凡的函数依赖,否则称为非平凡的函数依赖
- 一个关系模式有 n
个属性,在它上面成立的所有可能的函数依赖有多少个?非平凡的函数依赖有多少个?
- 函数依赖:\(4^n\)
- 平凡的函数依赖:\(3^n\)
- \(\sum{n \choose i}2^i=\sum{n \choose i}2^i1^{n-i}=(2+1)^n=3^n\)
- 非平凡的函数依赖:\(4^n-3^n\)
- 如果 R(U) 的候选码是整个属性集 U,这称为全码
- 例如选课表,只有两个属性(学号、课程号)
- 一个全码的关系模式存在非平凡的函数依赖吗?
- 不存在
- 如果存在 \(A\to B\),则存在一个候选码 \(A\),而且 \(A\) 不是整个属性集
- 如果存在非平凡关系依赖 \(A\to B\),则 \(B\) 可以不作为码的一部分
部分函数依赖
- 如果 \(X\to Y\),且对于任意 \(X\) 的真子集 \(X'\),都有 \(X′\not\to Y\),则称 \(Y\) 对 \(X\) 完全函数依赖,记作 \(X\overset{f}{\to} Y\)
- 否则称 \(Y\) 对 \(X\) 部分函数依赖,记作 \(X\overset{p}{\to} Y\)
- 如果在一个关系模式里面存在部分函数依赖的话,则是一个不好的设计
例子
- (sno, cno) \(\overset{f}{\to}\) grade
- (sno, cno) \(\overset{p}{\to}\) sname
传递函数依赖
- 如果关系模式中存在传递函数依赖,则也是一种差的设计
- 在 \(R(U)\) 中,如果 \(X\to Y,Y\to Z,Y\not\to X,Z\nsubseteq Y\),则称 \(Z\) 对 \(X\) 传递函数依赖
- 排除 \(Z\nsubseteq Y\) 原因
- 平凡函数依赖是一定成立的,关系模式中存在这样的函数依赖是正常的
- 排除 \(Y\not\to X\) 原因
- 说明 \(X,Y\) 都是候选码
- 多个候选码,在在关系模式的设计中是允许的
- 如何把函数的部分依赖整理成传递函数依赖的形式?
- \(X'\subset X,X\to Y,X'\to Y\)
- \(X\to X',X'\to Y\)
- 部分函数依赖一定能够转化为传递函数依赖
函数依赖的方式定义之前的码
- 超码
- 设 \(K\) 为 \(R(U,F)\) 的属性或属性组,若 \(K\to U\),则称 \(K\) 为 \(R\) 的超码
- 候选码
- 设 \(K\) 为 \(R(U,F)\) 的超码,若 \(K\overset{f}{\to} U\),则称 \(K\) 为 \(R\) 的候选码
- 主属性
- 包含在每一个候选码中的属性,称作主属性
- 候选码属性集的并,而不是交
- 例如属性集 (A,B,C),候选码 A, (B,C),则主属性是 A,B,C
- 包含在每一个候选码中的属性,称作主属性
- 非主属性
- 不包含在任何候选码中的属性称为非主属性
- 全码
- 关系模式的码由整个属性组构成,如 SPJ
范式
- 一个不好的设计的例子
- 学号,姓名、系号、系主任、选修课程、成绩

- 范式是对关系的不同数据依赖程度的要求
- 通过模式分解将一个低级范式转换为若干个高级范式的过程称作规范化(概念的纯粹化)
- 排除法:在某一的范式中,不存在某些类型的函数依赖
1NF
- 关系中每一分量不可再分,也即不能以集合、序列等作为属性值
1NF 与查询效率的折中
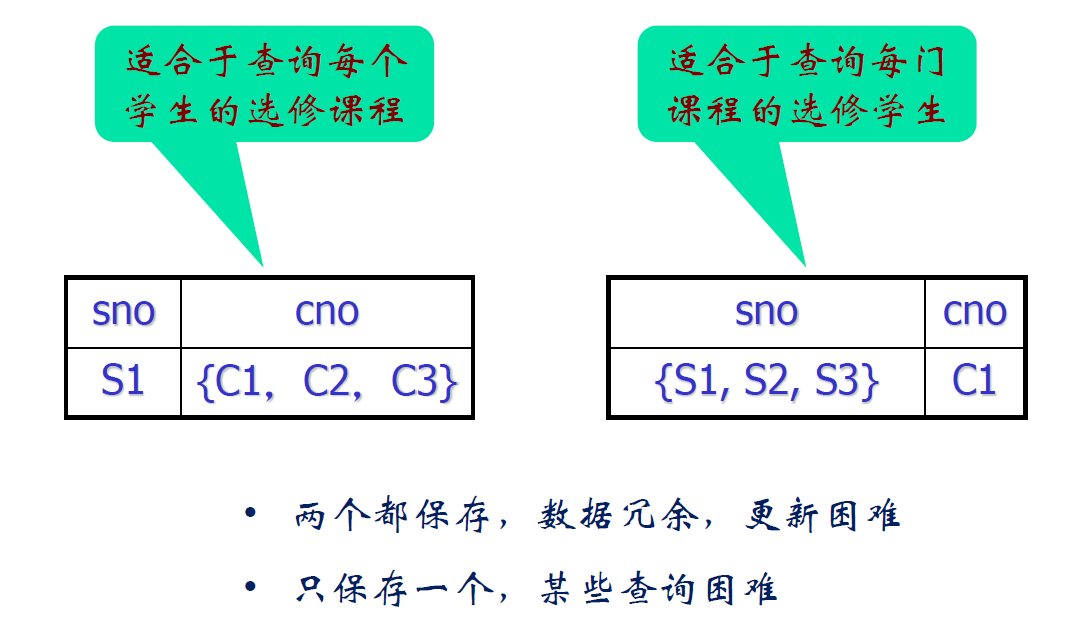
1NF 与应用对属性粒度的处理需求
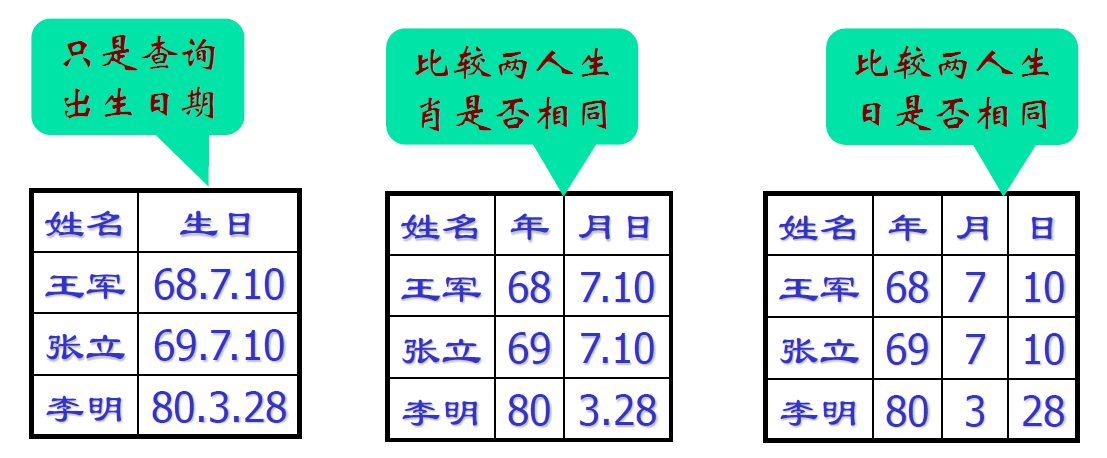
- 分量是否需要再分,与具体应用有关
- 如果用到值的一部分,则需要进一步分割,否则需要应用编码解析
1NF 与数据质量的控制准则
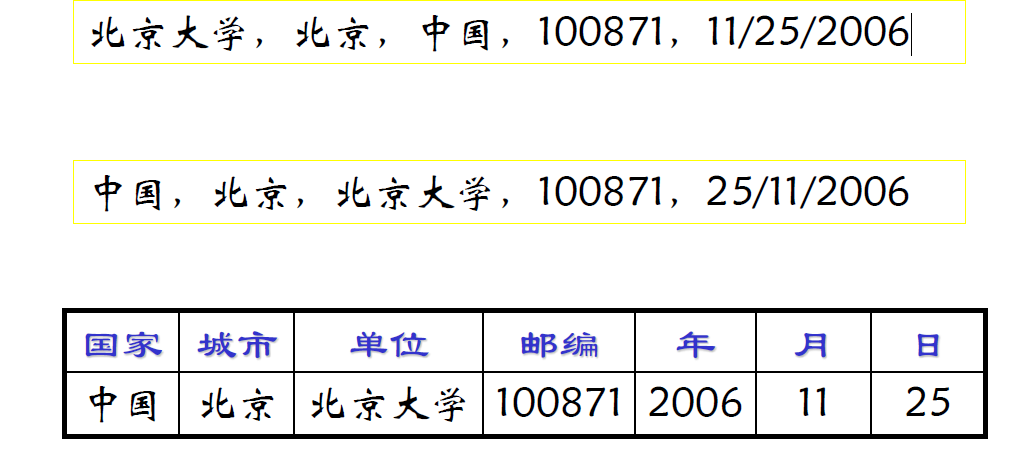
- 较细的原子粒度有助于标准化,施加约束,避免输入错误,从而提高数据质量
- 例如通讯地址,如果保存为一个属性,则输入格式可能不统一,导致解析困难
1NF 关系模式的不良特性

- 基于上面的例子
- 插入异常:如果学生没有选课,关于他的个人信息及所在系的信息就无法插入
- 删除异常:如果删除学生的选课信息,则他的个人信息及所在系的信息也随之删除
- 更新异常:如果学生转系,若他选修了 k 门课,则需要修改 k 次
- 数据冗余:如果一个学生选修了 k 门课,则有关他的所在系的信息重复
2NF
- 若 R \(\in\) 1NP ,且每个非主属性完全依赖于码,则称 R \(\in\) 2NF
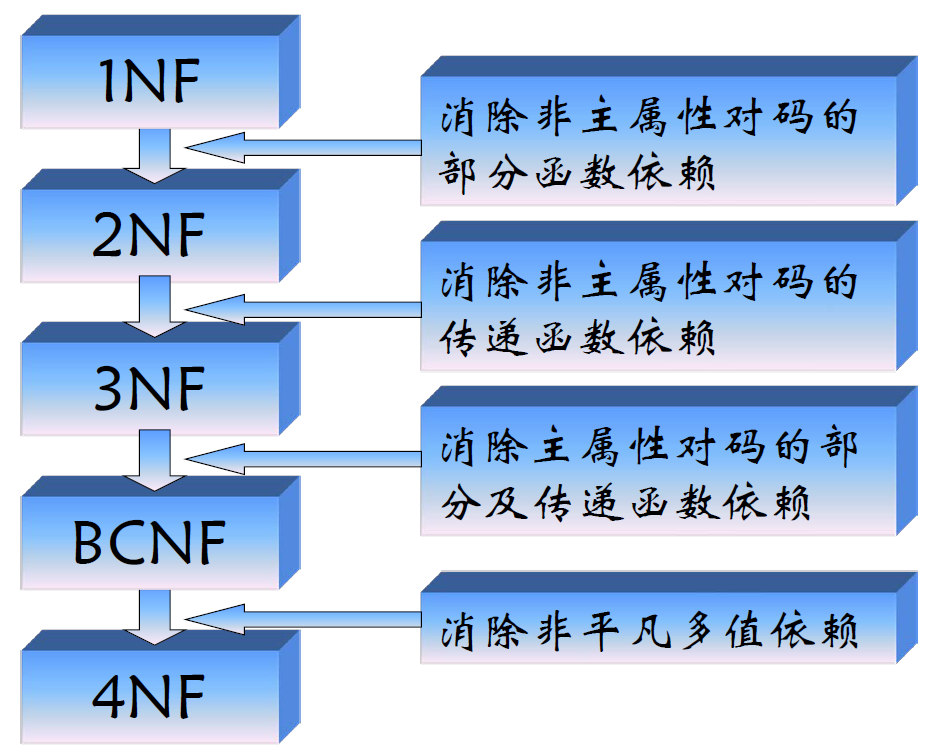
- 2NF 消除了非主属性对码的部分依赖
- 不要求主属性对码没有部分依赖
如何将关系模式改进到 2NF
- 非主属性有两种,一种完全依赖于码,一种部分依赖于码,据此将属性集划分为两部分
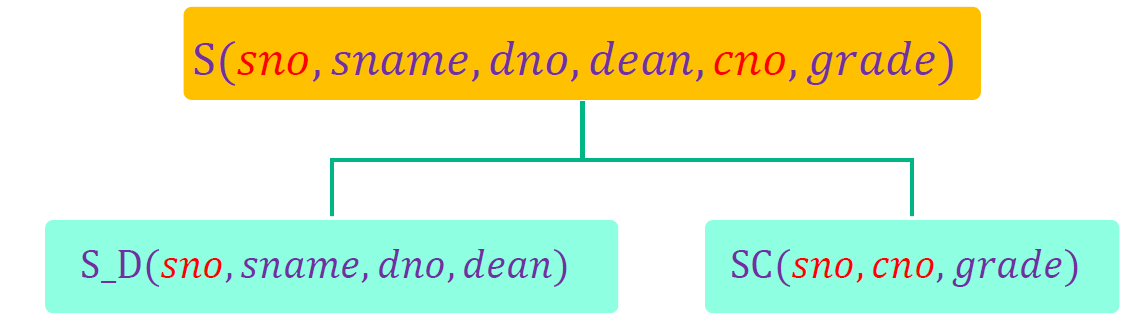
- 关系模式R(A,B,C,D),给出它的一个函数依赖集,使得码为 AB,并且 R 属于
1NF 而不属于 2NF
- 设置一个部分函数依赖即可
\[ AB\to C,B\to D \]
- 但是这样子的设计还是存在传递函数依赖
- sno 决定 dno,dno 决定 dean
2NF关系模式的不良特性
- 插入异常:如果系中没有学生,则有关系的信息就无法插入
- 删除异常:如果删除某系中全部学生,则该系的系主任信息也随之删除
- 更新异常:如果学生转系,不但要修改 dno,还要修改 dean
- 数据冗余:每个学生都存储了其系主任的信息
3NF
关系模式 \(R(U)\) 中,若不存在这样的码 \(X\),属性组 \(Y\) 及非主属性 \(Z(Z\not\subseteq Y)\),使得 \(X\to Y,Y\to Z,Y\not\to X\) 成立,则称 R \(\in\) 3NF
3NF 的目标是消除非主属性对码的传递依赖
如何将关系模式改进到3NF
- 砸断函数依赖的传递链
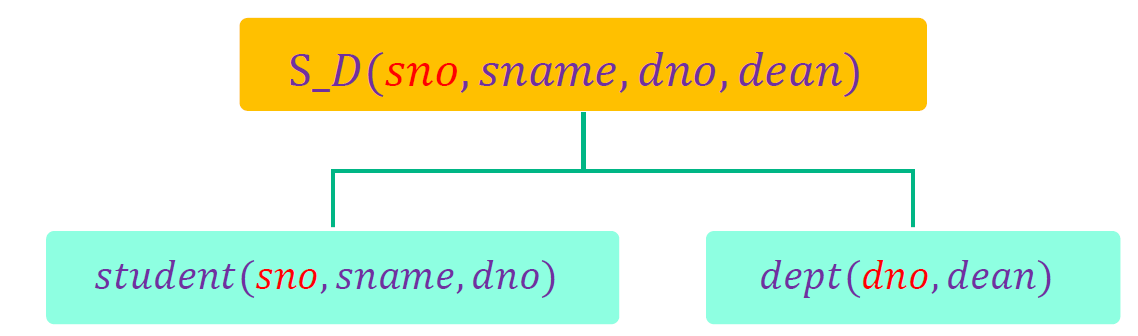
- 关系模式R(A,B,C,D),给出它的一个函数依赖集,使得码为 AB,并且 R 属于
2NF 而不属于 3NF
- 设置一个传递函数依赖即可(当然不能存在部分函数依赖)
\[ AB\to C, C\to D \]
- 正常情况下数据库的设计要求达到 3NF 就可以了
3NF 的问题
- 没有限定主属性的函数依赖
主属性部分依赖的例子:STC
- 关系模式:STC(sno,tno,cno)
- 每位老师只教授一门课:tno \(\to\) cno
- 某学生选定一门课,就对应一位老师:(sno,cno) \(\to\) tno
- 候选码:(sno, cno)、(sno, tno)
- STC \(\in\) 3NF
- 没有非主属性,因此是满足 3NF 的
3NF 的不良特性
- 插入异常:如果没有学生选修某位老师的任课,则该老师担任课程的信息就无法插入
- 删除异常:删除学生选课信息,会删除掉老师的任课信息
- 更新异常:如果老师的授课信息有所改动,则所有选修其课程的学生元组都要做改动
- 数据冗余:每位学生都存储了老师的授课信息
为什么给主属性留后门
- 一种折衷的考虑
BCNF
- 关系模式 \(R(U)\) 中,对于属性组 \(X,Y\),若 \(X\to Y,Y\not\subseteq X\) ,那么 \(X\) 必是码,则 R \(\in\) BCNF
- BCNF:所有属性都由码直接决定
- 所有非平凡的函数依赖的左边都需要是候选码
如何将关系模式改造成BCNF的
- 将属性划归到以决定它的属性作为码的关系模式中
- 3NF 中的例子 STC 是不属于 BCNF 的
- STC (sno,tno,cno)
- 修改为 (sno,tno),(tno,cno)
例子
- (sno, cno, order) 表示学生选修课程的名次(名次各不相同)
- 函数依赖
- (sno, cno) \(\to\) order
- (cno, order) \(\to\) sno
- 候选码:(sno, cno) 、(cno, order)
- 是属于 BCNF 的,函数依赖的左边都是属于候选码
3NF 和 BCNF 的比较
- 比较下面两个模式各自的优缺点
- 模式一:STC(sno,tno,cno)
- 模式二:ST(sno,tno), TC(tno,cno)
- 为什么有时会需要 3NF 而非 BCNF 的模式设计?
- BCNF 可能会导致表分的过碎,表的数目过多,可能对一些复杂的查询造成性能上的影响
- 例如原始的 STC 表中是有函数依赖 (sno,cno) \(\to\) tno 的,但是分开成 ST、C 两张表之后,这个函数不能体现了。这样我们可以在 ST 表(全码)中随意插入数据,而这样插入的数据可能不不满足函数依赖 (sno,cno) \(\to\) tno
- 全码是 BCNF 的
3NF 的另外一种定义
- 关系模式 R 中的函数依赖 \(X\to
Y\),必须满足下述条件之一:
- \(X\to Y\) 是平凡的函数依赖
- X 是 R 的码
- Y 是主属性
- 上面表示,如果 Y 是主属性的话,则不要求 X
是候选码,这样允许函数传递依赖
- Z \(\to\) X \(\to\) Y
- 3NF 允许存在主属性对码的不良依赖
BCNF 不良依赖的例子
- 关系模式 TEACH(cno, tno, bno)
- 一门课程由多个教员担任
- 一门课程使用相同的一套参考书
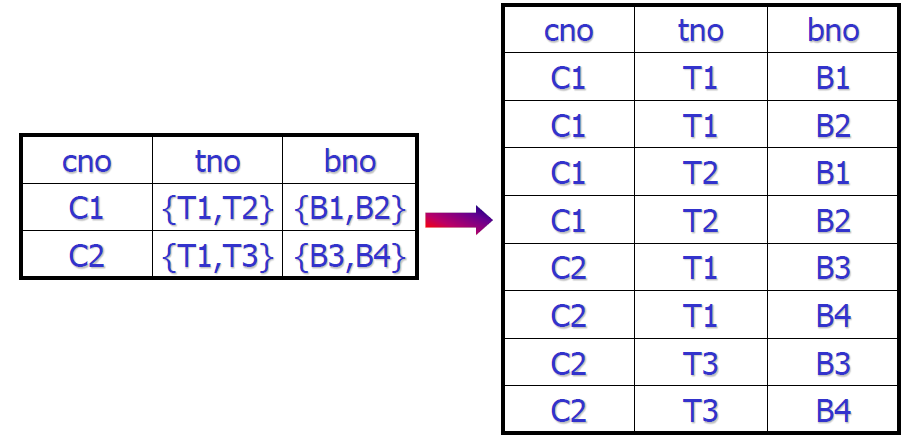
- 码是 (cno, tno, bno),全码,属于 BCNF
- 数据冗余很严重
- 如果有一门课程没有参考书的话,就无法插入数据
BCNF 的不良依赖
- 插入异常:当某门课程增加一名教员时,其有多少本参考书就必须插入多少个元组
- 删除异常:当删除一门课程的某个教员或者某本参考书时,需要删除多个元组
- 更新异常:当一门课程的教员或参考书作出改变时,需要修改多个元组
- 数据冗余:同一门课的教员与参考书的信息被反复存储多次
BCNF 冗余的根源
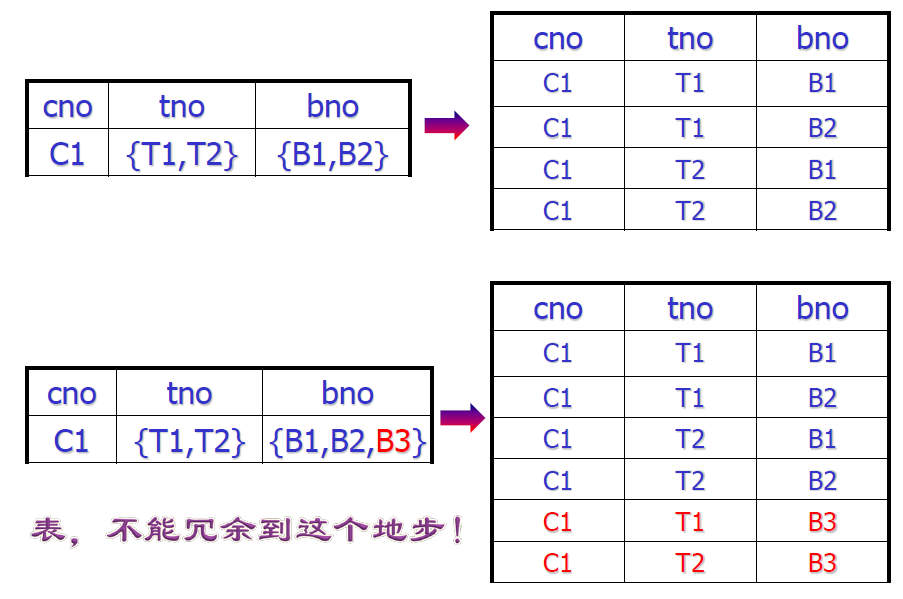
- 能否使用如下精简的表示

- 信息都还在,是完整的
- 问题
- 语义上是有问题的
- 删除的时候有问题,删除 B1 会把 T1 也删除掉
- 对等原则:标红的额外两行并不能提供更多信息,他们的存在纯粹是为了保证 tno 和 bno 彼此取值无关
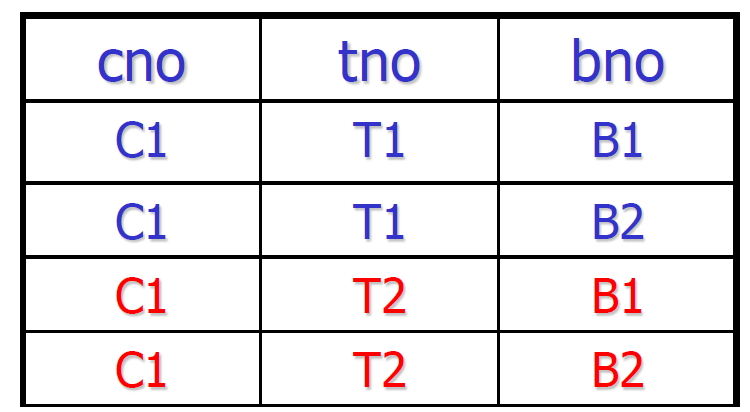
多值依赖
多值依赖的描述型定义
- 关系模式 \(R(U)\),\(X,Y,Z\subseteq U,Z=U-X-Y\),多值依赖 \(X\to\to Y\) 成立当且仅当
- 对 \(R(U)\) 的任一关系 \(r\),给定的一对 \((x,z)\) 值对应有一组 \(Y\) 的值,这组值仅仅决定于 \(x\) 值而与 \(z\) 值无关
- 一个例子:CTB
- cno \(\to\to\) tno

- 关系模式中的除法
\[ \forall xz,Y_{xz}=Y_x \]
多值依赖的形式化定义
- 关系模式 \(R(U)\),\(X,Y,Z\subseteq U,Z=U-X-Y\)
- 对 \(R(U)\) 的任一关系 \(r\),若存在行 \(t_1,t_2\) 使得 \(t_1[X]=t_2[X]\)
- 那么就必然存在行 \(t_3,t_4\),使得 \(t_3=(t_1[X],t_1[Y],t_2[Z]),t_4=(t_2[X],t_2[Y],t_1[Z])\)
- 则称 \(Y\) 多值依赖 \(X\),记作 \(X\to\to Y\)
理解
- 结合上面的例子,交换 t[Z] 之后还是存在在表中,说明 Z 和 Y 无关
- 对等原则
例子
| A | B | C |
|---|---|---|
| a1 | b1 | c1 |
| a1 | b1 | c2 |
| a2 | b1 | c1 |
| a2 | b1 | c3 |
- 是否满足 \(C\to\to B\)
- 满足
- 交换 A 还在表中
- 改成满足 \(B\to\to C\),需要加入那些行
| A | B | C |
|---|---|---|
| a1 | b1 | c3 |
| a2 | b1 | c2 |
多值依赖的基本性质
- 多值依赖具有对称性
- 若 \(X\to\to Y\),则 \(X\to\to Z\),其中 \(Z=U-X-Y\)
- 函数依赖是多值依赖的特例
- 若 \(X\to Y\),则 \(X\to\to Y\)
- 若 \(X\to\to Y\),\(U-X-Y=\emptyset\),称 \(X\to\to Y\) 为平凡的多值依赖
4NF
- 关系模式 \(R(U)\in 1NF\) ,对于非平凡的多值依赖 \(X\to\to Y(Y\not\subseteq X)\),X 含有码,则称 \(R\in 4NF\)
- 非 4NF 的主要弊端:数据冗余非常大
- 如下,不满足 4NF
- cno \(\to\to\) tno 不满足
- cno \(\to\to\) bno 不满足
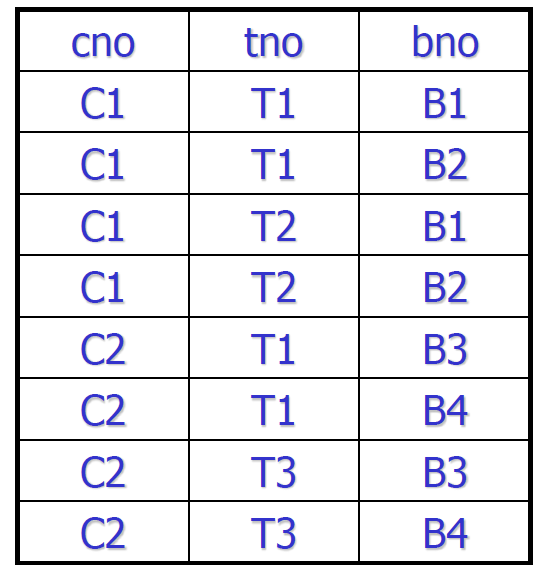
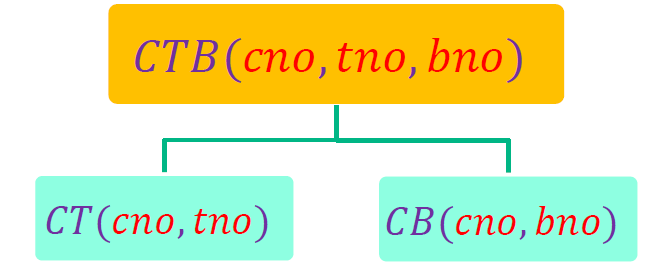
如何将关系模式改造为4NF的
- 多值属性单独放在独立的关系模式中
多值依赖与函数依赖
多值依赖与函数依赖的基本区别
- 相等产生依赖
- 函数依赖规定某些元组不能出现在关系中
- 现有的行可能会排斥新来的行
- 元组产生依赖
- 多值依赖要求某种形式的其它元组必须在关系中
- 现有的行要求新来的行同时插入一些其他行
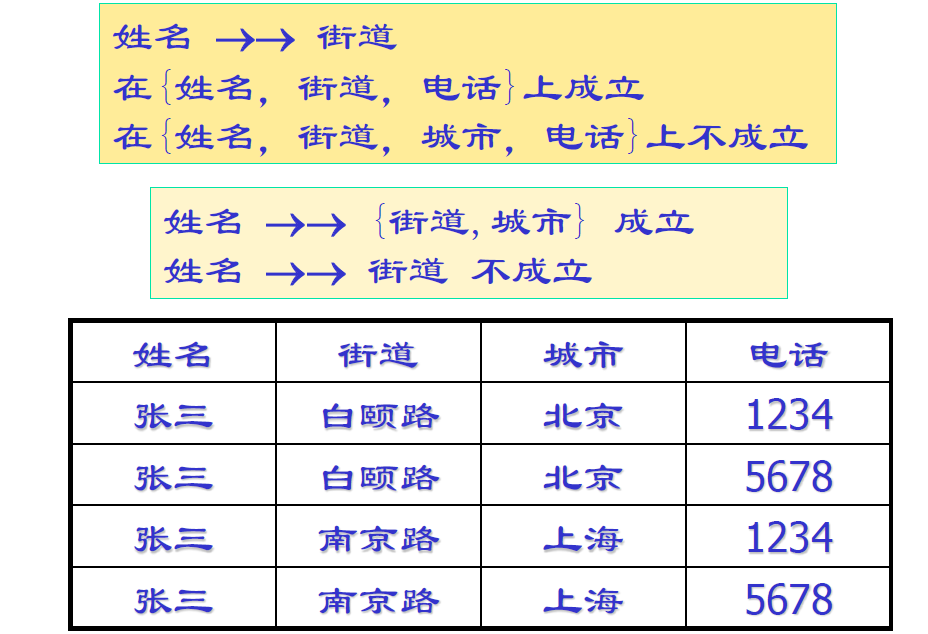
多值依赖与函数依赖有效性范围的不同
- \(X\to Y\) 的有效性仅决定于 \(X,Y\) 属性集上的值,,它在任何属性集 \(W(XY\subseteq W\subseteq U)\) 上都成立
- \(X\to\to Y\) 在属性集 \(W(XY\subseteq W\subseteq U)\) 上成立,但在
\(U\) 上不一定成立
- 只能说明 Y 和 W-X-Y 无关
- 例如 \(A\to\to B\) 在 ABC上成立,在 ABCD 上不一定成立
- 例子如下
- 有效性
- 监视函数依赖:更新、插入
- 监视多值依赖:更新、插入、删除
- 若 \(X\to\to Y\) 在属性集 \(W(XY\subseteq W\subseteq U)\) 上成立,则称 \(X\to\to Y\) 为 \(R(U)\) 的嵌入式多值依赖
- 若 \(X\to\to Y\) 在属性集 U上成立,则 \(X\to\to Y\) 在属性集 \(W(XY\subseteq W\subseteq U)\) 上成立
- 若 \(X\to Y\) 在 \(R(U)\) 上成立,则对于 \(\forall Y'\subseteq Y\) ,均有 \(X\to Y'\) 成立
- 若 \(X\to\to Y\) 在 \(R(U)\) 上成立,则对于 \(\forall Y'\subseteq Y\) ,不能保证有 \(X\to\to Y'\) 成立
- 不能保证 Y' 和 U-X-Y' 是否相关
- 例子如下

验证函数依赖和多值依赖
- 函数依赖 \(A\to B\) :下式为空
\[ \sigma_{R.A=S.A\land R.B\ne S.B}(R\times \rho_S(R)) \]
- 多值依赖 \(A\to\to B\)
- C 的取值和 B 无关
\[ R=\prod_{AB}(R)\bowtie\prod_{AC}(R) \]
连接依赖
- \(R_1(U_1),R_2(U_2),\cdots,R_n(U_n)\) 是 \(R(U)\) 的一个分解,\(r\) 是 \(R(U)\) 上的一个关系,若 \(r=\bowtie_{i=1}^{n}\prod R_i(r)\)
- 则称 \(r\) 满足连接依赖 \({}^\ast(R_1,R_2,\cdots,R_n)\)
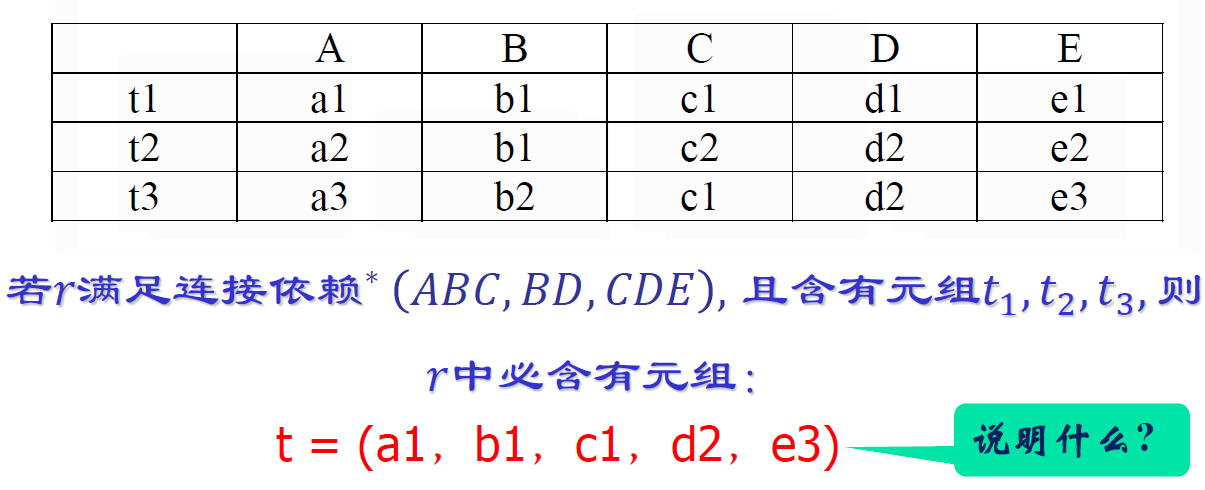
- 说明存在冗余
- 现实中很少考虑连接依赖,检测代价太高
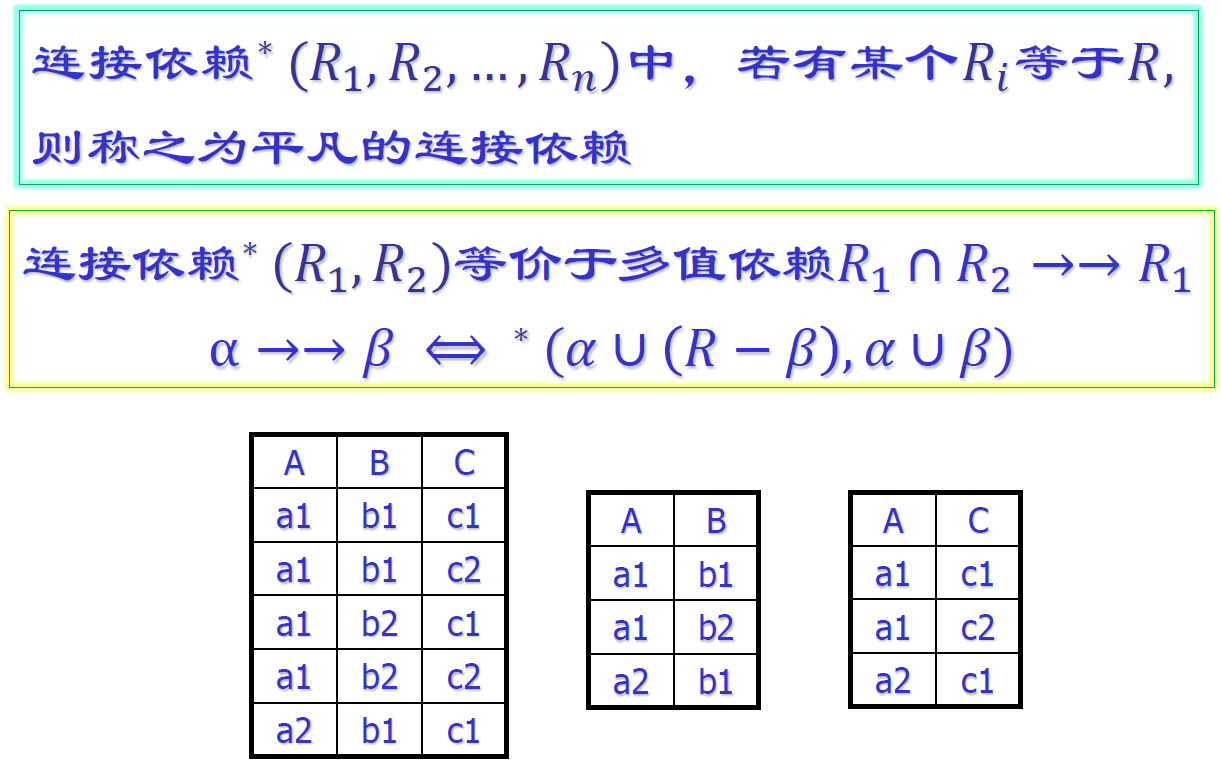
- 平凡连接依赖
- 连接依赖与多值依赖
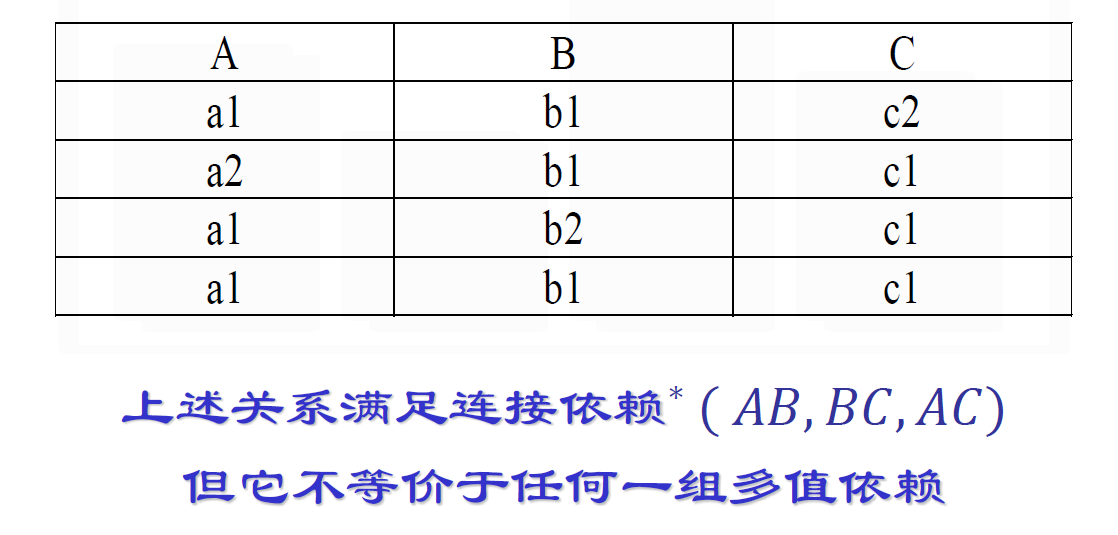
PJNF
- 投影-连接范式(PJNF)
- 若\(R\in PJNF\),则对于 \(R\) 的任一连接依赖 \({}^\ast(R_1,R_2,\cdots,R_n)\)
必是下述情况之一:
- \({}^\ast(R_1,R_2,\cdots,R_n)\) 是平凡的连接依赖
- 每个 \(R_i\) 是 \(R\) 的超码
一些其他问题
- 任何一个二目关系模式 \(R(A,B)\) ,一定属于 BCNF 吗?一定属于4NF 吗?
- 一个候选码全是单属性的关系模式最高一定可以达到第几范式?
- 一个全是主属性的关系模式最高一定可以达到第几范式?
- 一个只有一个候选码的 3NF 关系模式是 BCNF 的吗?
- 一个全码的关系模式最高一定可以达到第几范式?
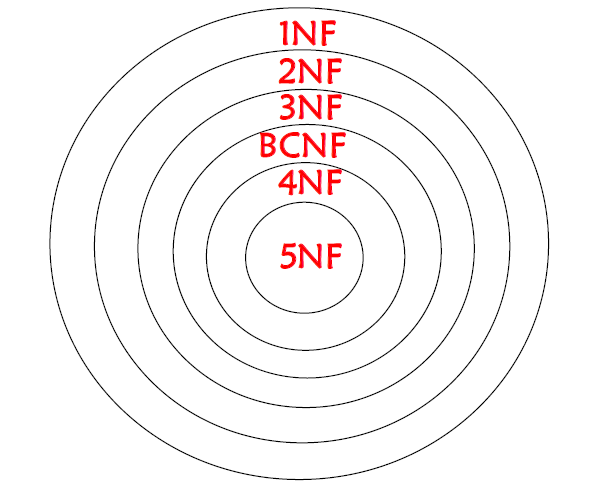
各种范式的关系
- 3NF \(\in\) 2NF

- BCNF \(\in\) 3NF

- PJNF \(\in\) 4NF

- 总结