GAMES202.闫令琪.08.实时全局光照(屏幕空间)(SSAO/SSDO)
- https://www.bilibili.com/video/BV1YK4y1T7yY
屏幕空间全局光照
屏幕空间
- 所有拿到的信息都是在屏幕上的
- 之后使用的信息只能是直接光照形成的结果
- 相当于是对得到的二维图像进行一个后处理
SSAO
- Screen Space Ambient Occlusion
- 屏幕空间环境光遮蔽
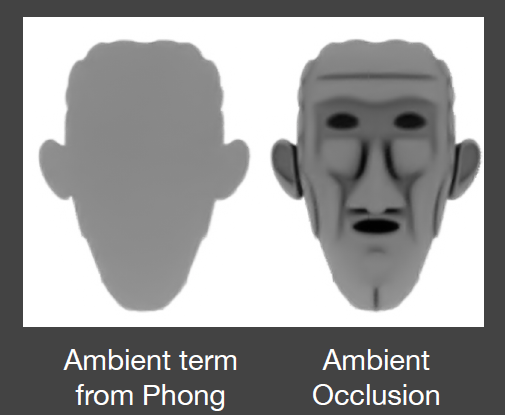
- AO 的结果:contact shadow
- 物体接触的地方会有阴影
- SSAO:对于全局光照的一个近似
- 屏幕空间内的信息进行计算
关键假设
- 我们不知道入射光的方向
- 我们可以假设,对于所有的 shading
point,所有的入射方向,光照都是一个常数
- 环境光
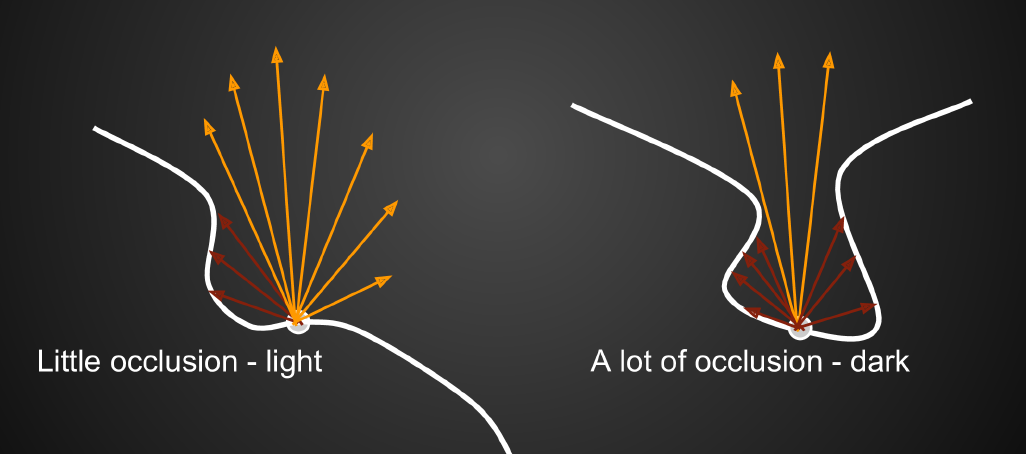
- 但是不同地方接受到的环境光的强度应该是不一样的,通过某种方式对于环境光的强度进行估计
- 同时我们假设所有的物体都是 diffuse 的
理论基础(环境光)
- 渲染方程
\[ L_o(p,\omega_o)= \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o) V(p,\omega_i)\cos\theta_i\,\mathrm{d}\omega_i \]
- 利用之前的经典不等式
- \(g(x)\):smooth / small support
\[ \int_\Omega f(x)g(x)\,\mathrm{d}x\approx \dfrac{\int_\Omega f(x)\,\mathrm{d}x}{\int_\Omega \,\mathrm{d}x}\cdot {\int_\Omega g(x)\,\mathrm{d}x} \]
- 近似结果
- 多了一项 \(\cos\theta_i\),后面会解释
- 可以把 \(\cos\theta_i\,\mathrm{d}\omega_i\) 整个看成是一项 \(\mathrm{d}x_{\perp}\)
\[ L_o(p,\omega_o)\approx {\color{blue}\dfrac{\int_{\Omega^+}V(p,\omega_i)\cos\theta_i\,\mathrm{d}\omega_i}{\int_{\Omega^+}\cos\theta_i\,\mathrm{d}\omega_i}} \cdot {\color{red}\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_i\,\mathrm{d}\omega_i} \]
- 蓝色部分
- 平均可见性
\[ {\color{blue}k_A}=\dfrac{\int_{\Omega^+}V(p,\omega_i)\cos\theta_i\,\mathrm{d}\omega_i}{\pi} \]
- 红色部分
- diffuse,BRDF 是常数
- 光照为 constant,L 为常数
- 都可以随便指定
\[ L_{i}^{indir}(p)\cdot\dfrac{\rho}{\pi}\cdot\pi=L_{i}^{indir}(p)\cdot\rho \]
- AO 可以理解为
- 平均的 visibility x 你给定的一个数
一种理解
\[ \int_\Omega f(x)g(x)\,\mathrm{d}x\approx \dfrac{\int_\Omega f(x)\,\mathrm{d}x}{\int_\Omega \,\mathrm{d}x}\cdot {\int_\Omega g(x)\,\mathrm{d}x}=\overline{f(x)}\int_\Omega g(x)\,\mathrm{d}x \]
- 我们可以认为,是在求一个 \(f(x)\) 在 \(g(x)\) 的定义域 \(\Omega\) 上求一个平均值
准确的条件
- \(g(x)\):smooth / small support
- 所以 AO 的拆分是准确的
- \(G\) 是常数
另一种理解
- 拆分后为什么多了一项 \(\cos\theta_i\)
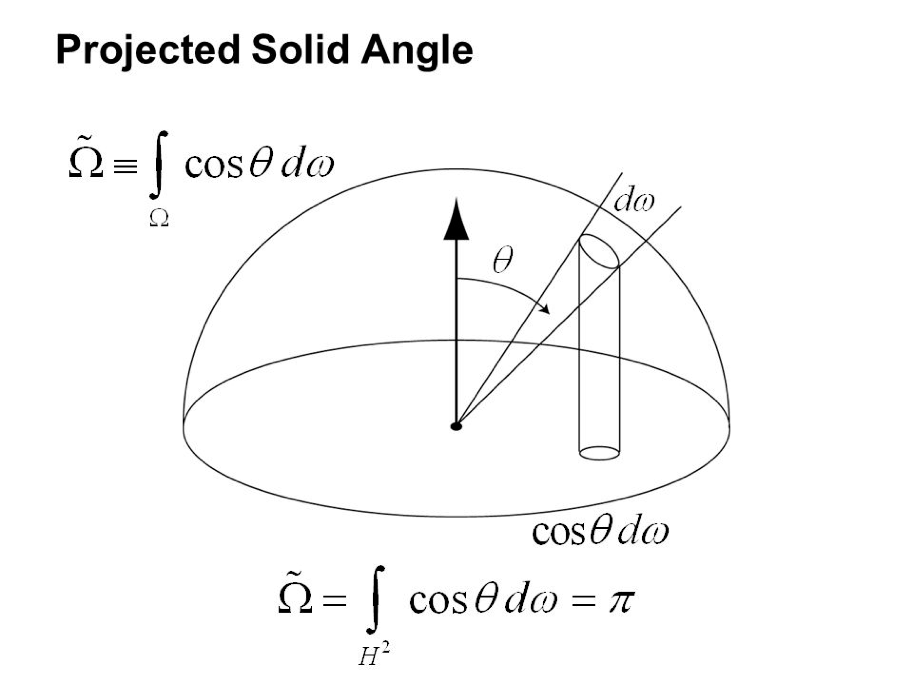
- \(\mathrm{d}x_{\perp}=\cos\theta_i\,\mathrm{d}\omega_i\) 刚好是立体角投影到平面上的结果
- 所以我们可以把 \(\cos\theta_i\,\mathrm{d}\omega_i\) 整个看成是一项 \(\mathrm{d}x_{\perp}\)
SSAO 的简单理解
- 光照为常数,BRDF 为常数
- 可以从积分项中拿出来
\[ \begin{aligned} L_o(p,\omega_o)&= \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o) V(p,\omega_i)\cos\theta_i\,\mathrm{d}\omega_i\\ &=\dfrac{\rho}{\pi}\cdot L_i(p)\cdot\int_{\Omega^+}V(p,\omega_i)\cos\theta_i\,\mathrm{d}\omega_i \end{aligned} \]
怎么求解可见性(屏幕空间)
- 对于某一个 shading point,我们对其法相半球进行采样,求平均可见性
- 发出 trace 光线,光线距离R,进行可见性判断
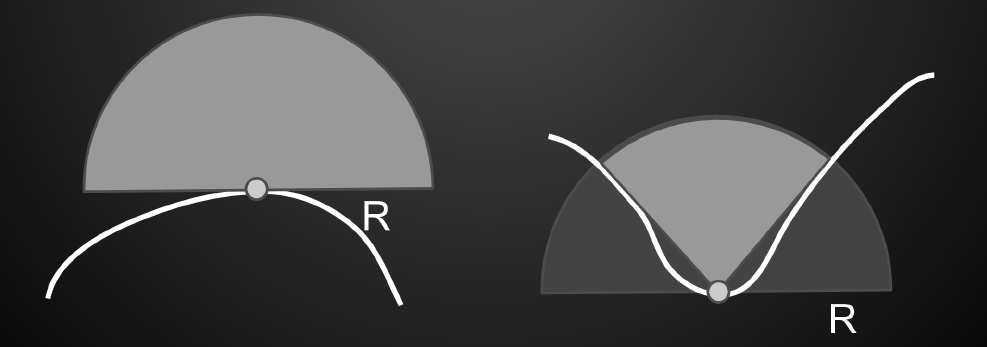
- 选取一个指定的半径 R
- R 不能太大,否则最终都会被挡住(想象一个封闭的屋子)
- R 不能太小,否则会忽略一些来自于更远的反射光
- trade off
实际求解可见性的方法
- 利用 z-buffer
- 直接去 trace 光线很难做
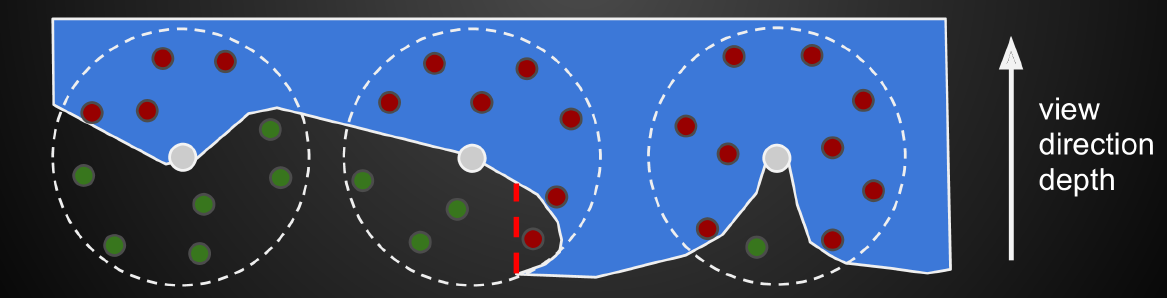
- 对于任何一个 shading point,我们对其周围半径 R 内的球体内进行采样
- 利用深度图(正常光栅化渲染管线渲染都会生成一张深度图)
- 对每一个采样点,我们将其和深度图中记录的深度作比较
- 采样点经过投影变换得到的深度值如果比深度图中记录的要大,说明被挡住了
- 但是这样子是有可能出错的,毕竟记录的是一个 2D 的信息
- 中间那幅图的红色虚线右边的点
- 它在物体外部,但是根据 SM 的出来的值是在物体内部
- SM 中无法记录复杂的几何信息
- 这样子的小错误在工业界是可以容忍的
- 早期使用的是整个球体的采样,而不是法向半球采样,实际上我们使用法相半球采样才是正确的
- 因为早期渲染管线,在最后无法保留法线的值,于是只能用整个球体的采样
- 早期的解决方案
- 只有在红点个数(被遮挡的点个数)过半的情况下,才开始考虑 AO
- 现在我们直接使用法向半球采样
SSAO 的问题
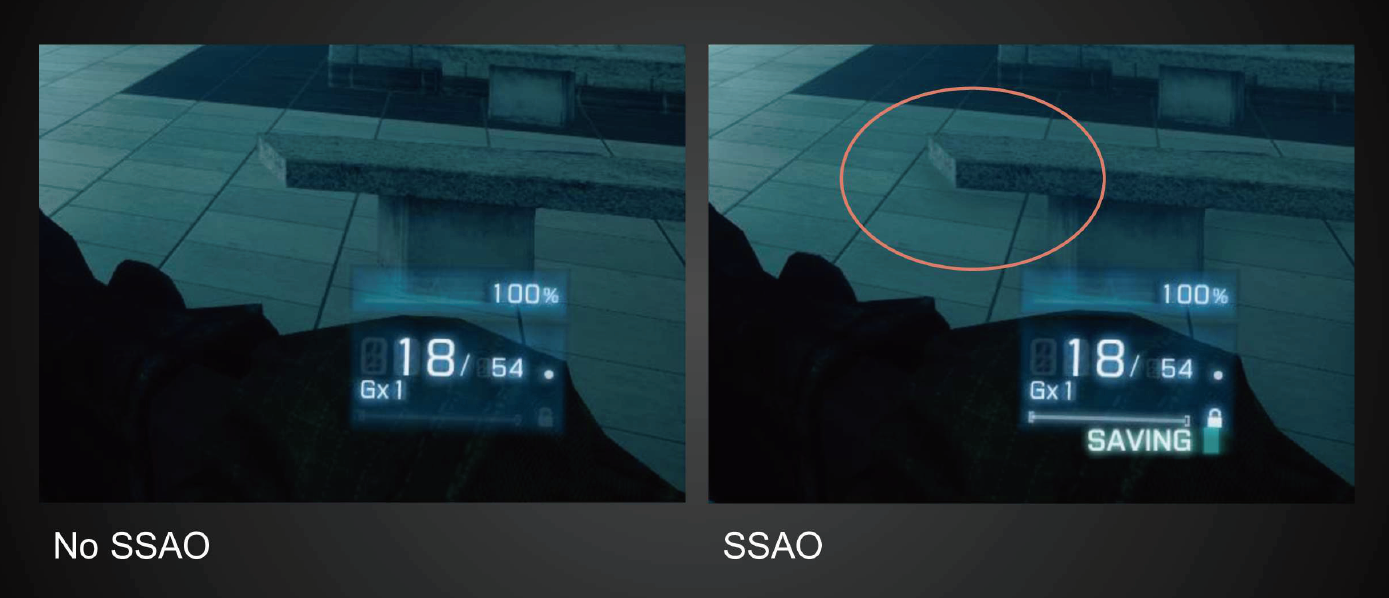
- 可能会出现一些虚假的 AO(false occlusion)
- 如右图中,石凳和地面应该没有接触,因此不应该有 AO 的效果,但是我们在之前简单的考虑遮挡,就会产生这样的现象
- 工业界的解决方案,使用一个半径 R,大于半径 R,我们认为不遮挡
- 采样点越多,AO 的效果越好
- 怎么在采样点少的情况下获得噪声比较小的结果
- 先做 AO,然后做一个高斯模糊(去噪)
HBAO
- Horizon based ambient occlusion
- SSAO 的改进
- 在法向半球内采样
- 考虑半径 R
SSDO
- 对 SSAO 的提高
- 对于间接光照,我们没必要假设所有方向来的光是一样的
- 我们在一定程度上是能够知道间接光照的
- 从屏幕空间中来

- SSAO 只能产生变亮变暗的效果,但是不能模拟颜色的变化
- 做法和 path tracing 很像
- 从 shading point 随机打出射线
- 如果射线击中了某个物体,产生间接光照
- 如果涉嫌没有击中物体,直接光照
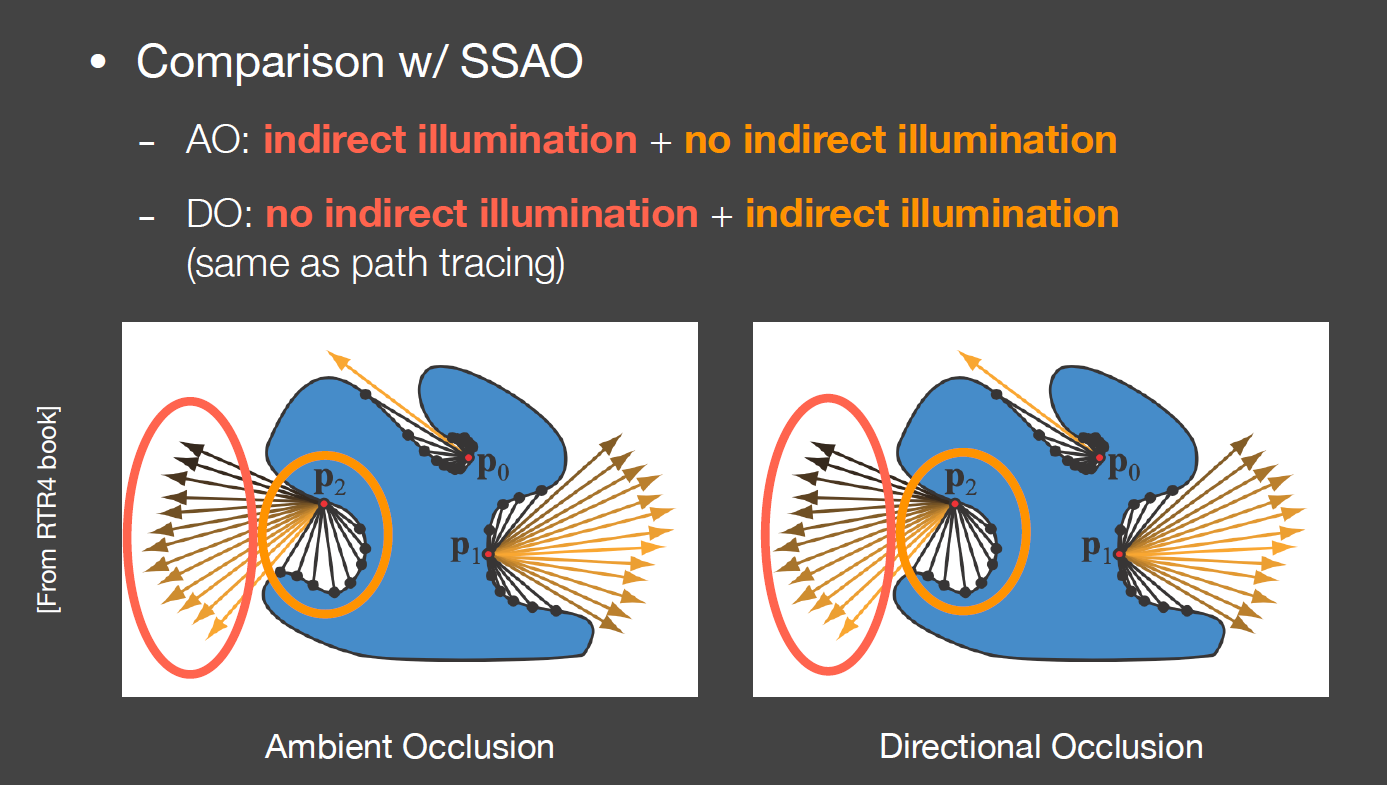
AO 与 DO
- AO 与 DO 的假设是完全相反的
- AO 假设间接光照来自于非常远的地方
- DO 假设间接光照来自于周围相近的地方
- 红色圈内的射线
- AO 认为有间接光照(没有被物体挡住)
- DO 认为没有间接光照(没有击中次级光源/物体)
- 黄色圈内的射线
- AO 认为没有间接光照(被物体挡住了)
- DO 认为有间接光照(接种了次级光源/物体)
SSDO 的实现
- 如果没有击中物体,没有间接光照(可能是环境光或者是直接光照)
\[ L_o^{dir}(p,\omega_o)= \int_{\Omega^+\;V=1}L_i^{dir}(p,\omega_i)f_r(p,\omega_i,\omega_o) \cos\theta_i\,\mathrm{d}\omega_i \]
- 击中其他物体,则需要计算间接光照
\[ L_o^{indir}(p,\omega_o)= \int_{\Omega^+\;V=0}L_i^{indir}(p,\omega_i)f_r(p,\omega_i,\omega_o) \cos\theta_i\,\mathrm{d}\omega_i \]
判断一个点是否可见
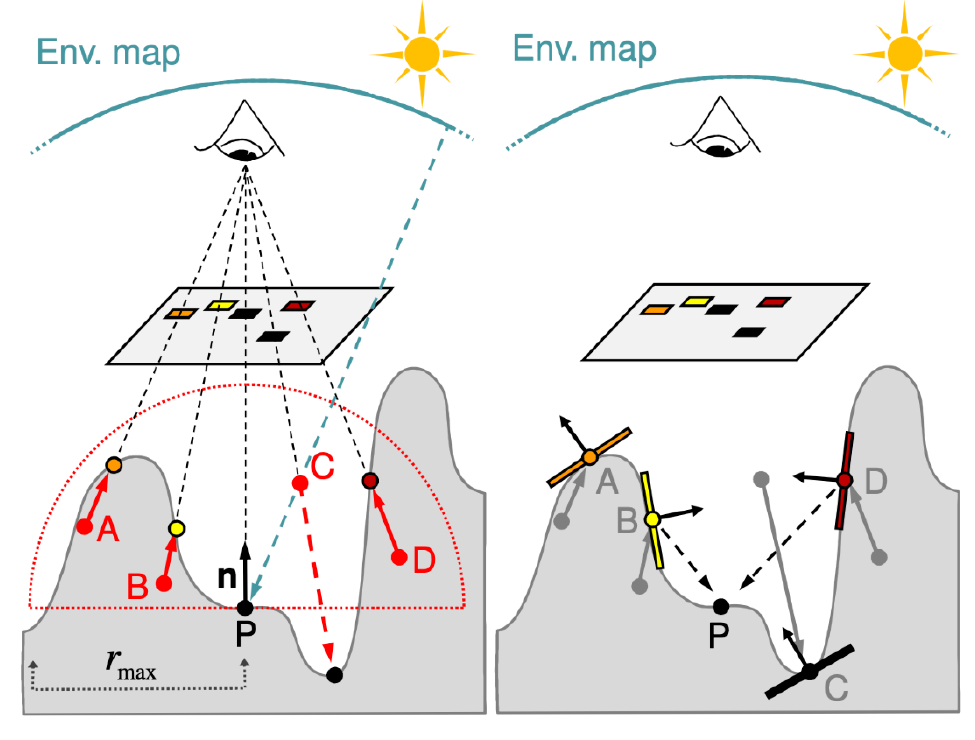
- 和 HBAO 一样
- 判断某个点是否可见,和 HBAO 同样的判断
- 深度与深度图中的记录相比较
- 限制半径 R
- 上图中
- C 点没有被挡住,因此可以计算环境光照(我们不太关心这一点)
- A、B、D 点被挡住了,因此我们需要计算这 3 个点对 shading point 的贡献
- 深度图中的点都是记录了 flux 等信息的(defered shading 的思想)
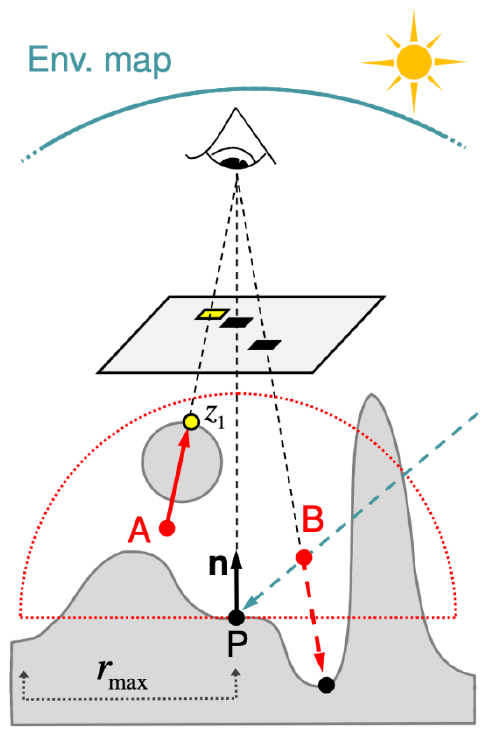
- 我们判断一个点是否对 P
点可见,使用其深度和深度图中记录值相比较,这是有问题的,例如下图中
- A 点对 P 点可见,但是我们判断为不可见
- B 点对视点可见,但是 PB 这个方向会被其他物体挡住
SSDO 评价
Pros
- 质量不错
- 轻量级计算
Cons
- 可见性(考虑得比较少)
- Screen space 丢失了信息
- 例如下图,我们将物体旋转之后,由于视点看不到背面,结果导致地上的反光没了

- SSDO 只能做到近处的贡献(只考虑了小范围内的贡献)