GAMES202.闫令琪.07.实时全局光照(3D空间)
- https://www.bilibili.com/video/BV1YK4y1T7yY
3D空间实时全局光照
- Global Illumination (GI) is important but complex
- GI:Global Illumination

one-bounce
- 实时渲染中,我们主要解决的全局光照之的主要是 one-bounce 的间接光照
- one-bounce
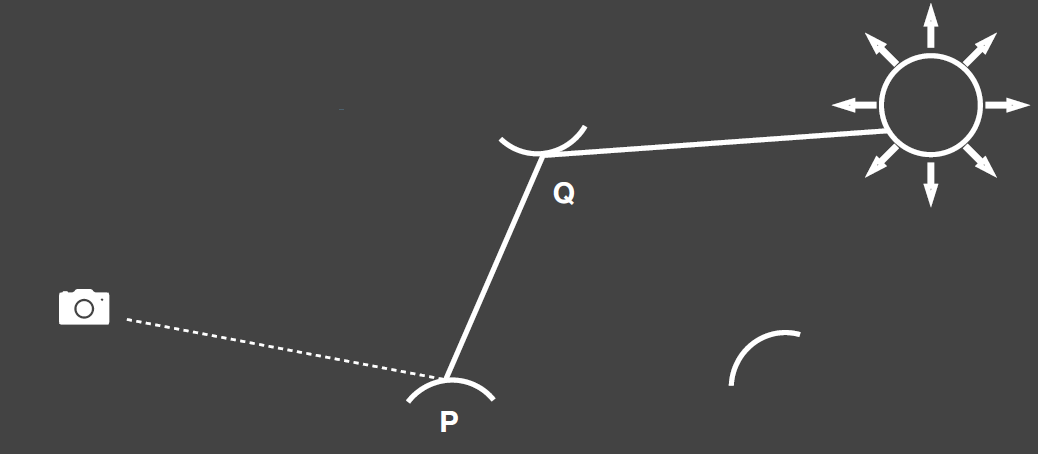
- 一切被光源直接照亮的物体,都可以作为次级光源去照亮其他物体
- 原始的光源:primary light source
分类
- 3D 空间的方法
- RSM
- VXGI
- 图像空间
- SSAO
- SSDO
- SSR
RSM
- Reflective Shadow Mapping
问题
- 那些部分可以被作为次级光源
- Shadow Mapping
- 每个次级光源对 shading point 的贡献是多少
- 把每一小区域都当做是面光源
- 采样方法
次级光源
- 使用 shadow map 解决
- 对于 SM 而言,认为每一个像素对应一个小片
- 同样的理解,我们可以把这些小片对应的区域都作为次级光源
- 计算量很大:采样
- 产生了一个问题,我们在计算次级光源 shading 的时候,我们是在 light 的位置去观察的,我们不知道这些次级光源之后用于渲染其他物体的时候的入射方向是什么(次级光源的出射方向不知道)
- 怎么让结果不依赖于出射方向呢?
- 经典假设:所有反射物(次级光源)都是 diffuse 的
怎么用次级光源去照亮
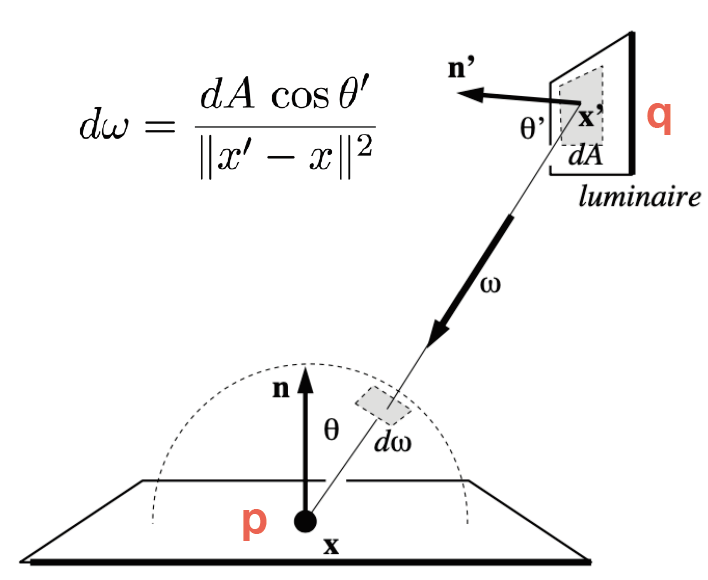
- 对(次级)光源采样
\[ \begin{aligned} L_o(p,\omega_o) &=\int_{\Omega_{patch}}L_i(p,\omega_i)V(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_i d\omega_i\\ &=\int_{A_{patch}} L_{i}(q\to p) V(q\to p)f_{r}(p, q\to p, \omega_{o})\dfrac{\cos\theta_p\cos\theta_q}{||p-q||^2}dA\\ \end{aligned} \]
- 如果 patch 的数量比较少,可以直接求和
- 对于次级光源,diffuse
- BRDF:\(f_r'=\dfrac{\rho}{\pi}\)
- 注意不是上面渲染方程里的,而是针对次级光源 p 处的,上面的是 q 处的
- \(L_i=f_r'\dfrac{\Phi}{dA}\)
- \(\Phi\):入射的 flux
- BRDF 的定义
- 带入渲染方程,发现不需要知道 patch 对应的大小(消掉了)
- 只需要知道 \(\Phi\) 即可
- BRDF:\(f_r'=\dfrac{\rho}{\pi}\)
- 可见性检测,V 很难做
- 不好算就不算了
- 论文中的系数
- 4 次方
- 和我们推导的是一致的
- 分子中 \(x-x_p\) 没有归一化,归一化之后是一样的
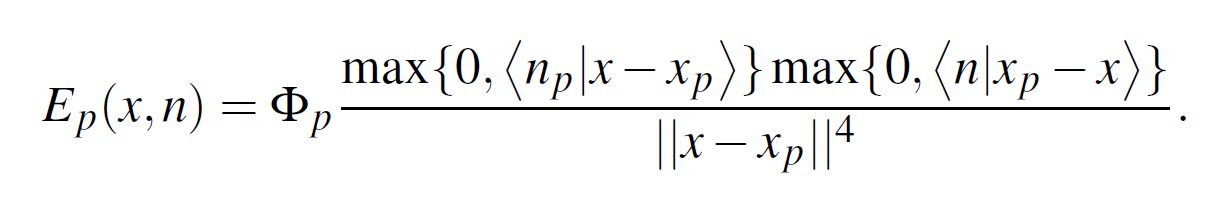
一些细节
- 不是所有的次级光源都会对 shading point 有贡献
- 可见性(很难)
- 距离
- 朝向
- 例如桌子上的点不会照亮 x 点
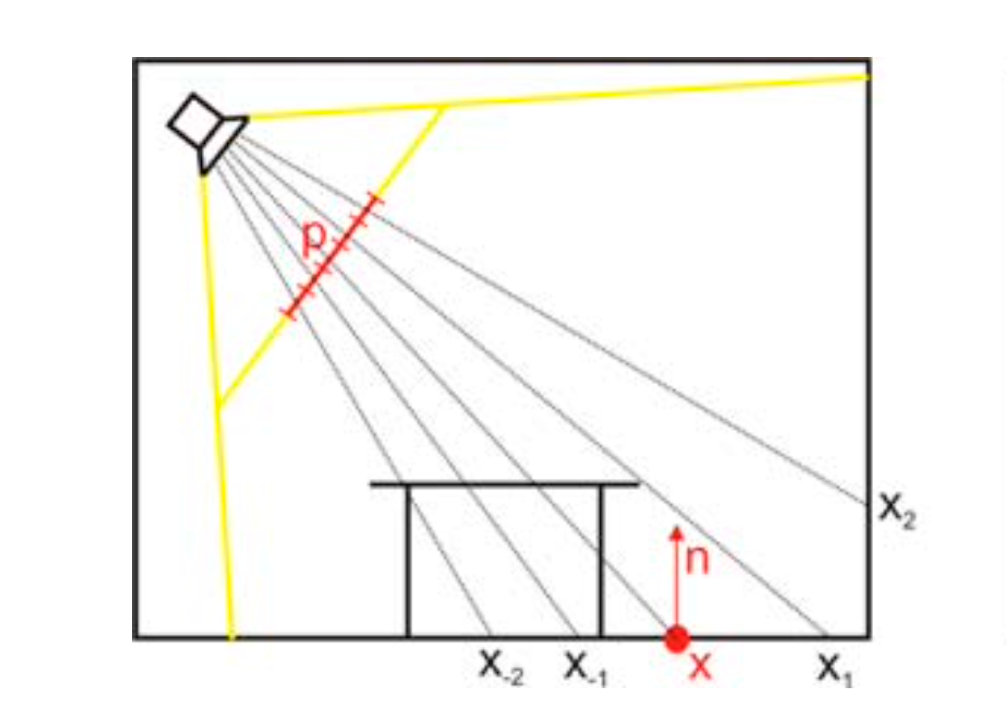
- 只需要找离 shading point 比较近的点采样
- 平方衰减
- 论文大胆的假设,在 SM 中离得比较近,表示在世界坐标系中离得比较近
- 加速采样
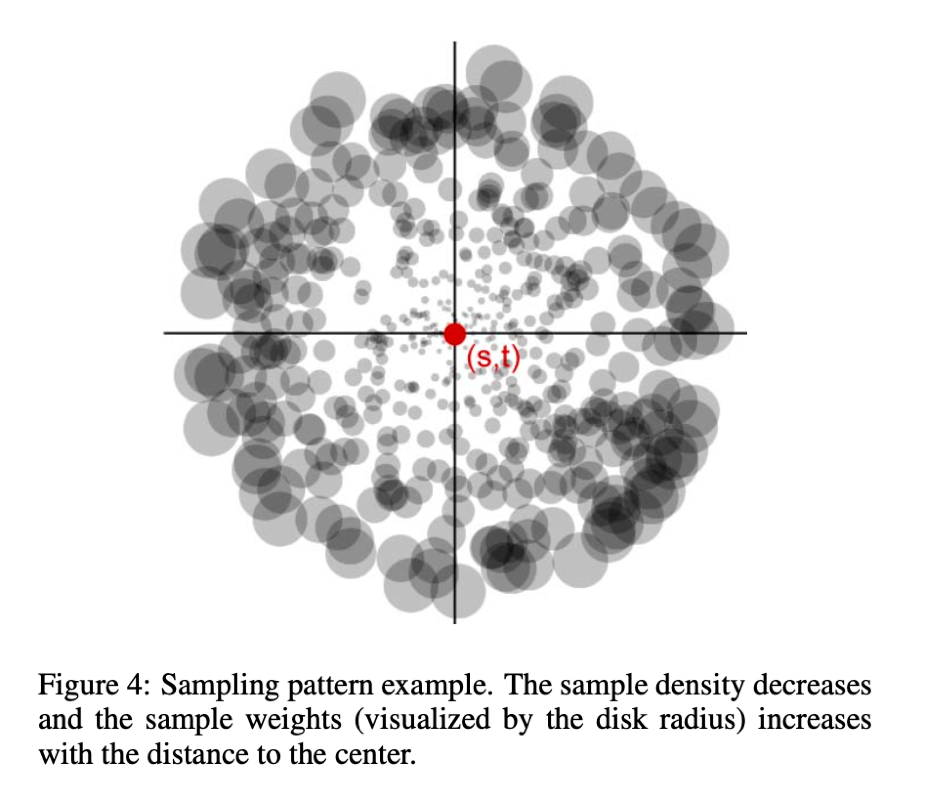
- 具体采样方法
- 近的点贡献大,多采样一点
- 远的点少采样一点,但是把面积做大一点
- 400 个 sample 效果就不错
- 存储开销
- shadow map(depth)
- flux
- 世界坐标系法向
- 世界坐标系位置
- RSM 对手电筒的模拟效果非常好
评价
- pros
- 很容易实现:基于 shadow map 算法
- cons
- 直接光源个数有多少个,就需要做多少个 SM(SM 原生问题)
- 次级光源照亮物体时没考虑可见性
- 很多假设:计算在次级光源处的 shading 的时候做了 diffuse 的假设
- 深度图之间的距离代替世界坐标系的距离
- 采样率和效率之间的 trade off
其他想法
- RSM 中的次级光源和离线渲染中的 VPL 非常接近
- virtual point light
- 认为 RSM 还是属于 3D 的方法,而不是图像空间的方法
- 因为准确记录了信息,而且第二个 pass 的时候还是在 3D 空间中计算的
LPV
- Light Propagation Volumes (LPV)
- 最早在 CryEngine3 中被提出
- Crisis 游戏
- 关键问题
- 对于每一个 shading point 能够很快的获得来自各个方向的 radiance
- LPV 的关键想法:radiance 直线传播,传播过程中是不变的
- 把场景划分为 3D 的网格
- Voxel 体素
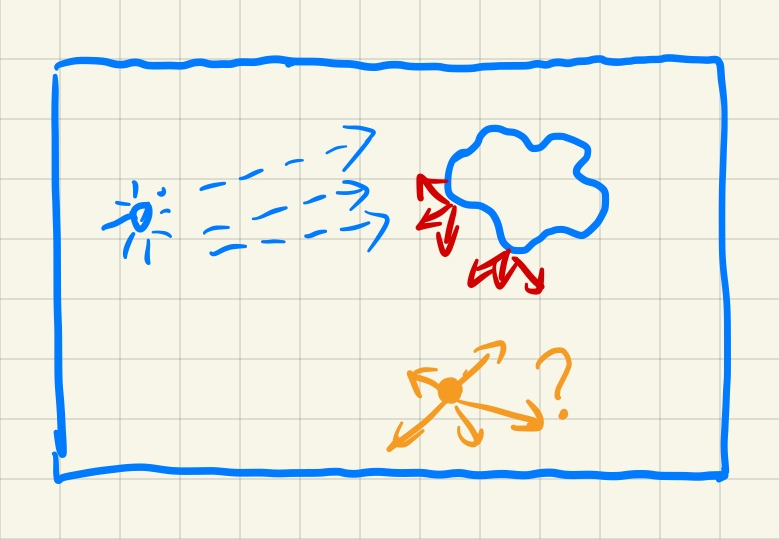
- 问题抽象(上图是一个 2D 的例子)
- 蓝色:直接光源
- 红色:被光源直接照亮的物体
- 黄色:询问来自各个方向的 radiance
算法步骤
- Generation of radiance point set scene representation
- 确定哪一些点会发出间接光照(次级光源)
- Injection of point cloud of virtual light sources into radiance
volume
- 把次级光源放到场景的网格中
- Volumetric radiance propagation
- 将 radiance 在网格中进行传播
- Scene lighting with final light propagation volume
- 直接利用这些 radiance 进行光照计算
Step 1: Generation
- 找到次级光源
- 可以简单地通过 RSM 找到
- 不一定需要使用所有的次级光源,可以对其进行一些采样
Step 2: Injection
- 首先将场景划分为 3D 的网格
- 对于每一个网格,我们找到网格内的次级光源
- 对于每个方向的 radiance 进行求和
- 使用 SH 进行压缩(2阶就够了)
- 使用 SH 压缩,于是只能得到一些相对低阶的项,因此对于 diffuse 场景支持较好
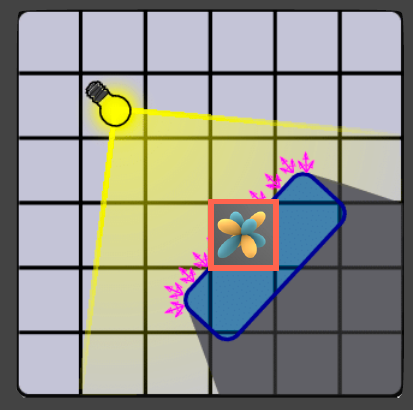
Step3: Propagation
- 对于每一个网格,考虑它周围的 6 个邻接的网格传播过来的 radiance
- 求和,然后使用 SH 进行压缩
- 实际操作可能是对每个点向周围 6 个面的传播
- 最终迭代至不动点
- 一般迭代四五次就能够稳定下来
- 在传播的过程中,我们不考虑可见性
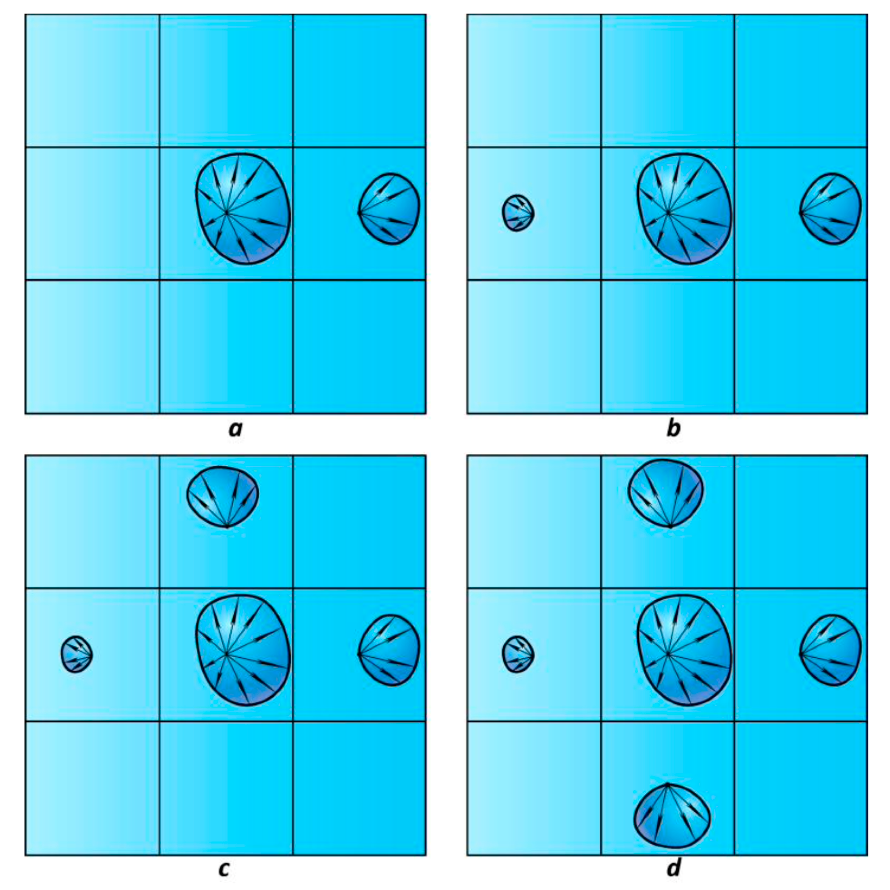
Step 4: Rendering
- 对于任意的 shading point,我们找到它位于哪一个具体的网格中,通过记录的不同方向的 radiance 进行计算
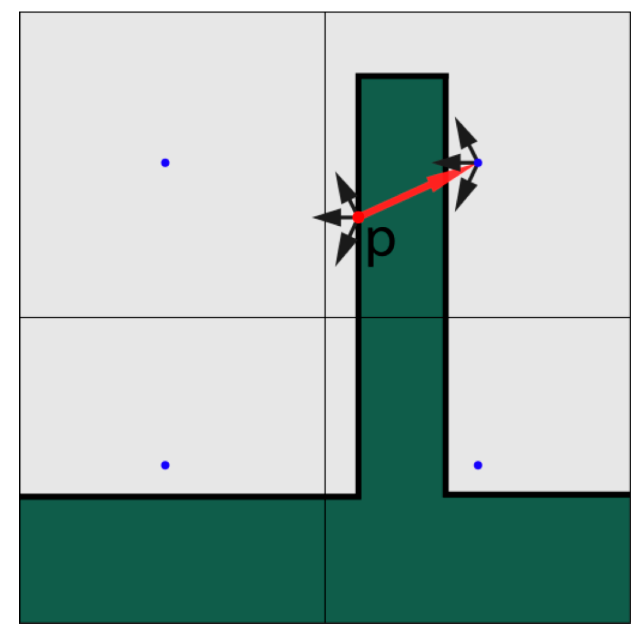
问题
- 如下图,我们将一个网格内的点的 radiance 都认为是一样的,但是实际上 p
点不会照亮对应网格中的蓝色点
- 造成 light leaking 的问题
- LPV 和 对比图

- 根本原因:网格的精度问题,如果存在某个场景中的几何粒度比网格要小,这样就可能会导致上面的现象
- 增大精度
- 存储开销变大
- propagation 不容易稳定,计算开销变大
- 工业界的实现会使用不同精度层次的网格
- 学术界叫法:multi-scale
- 工业界叫法:cascaded
- 对于每一个光源,都需要用一次 RSM 算法
- 注入之后的传播只需要一次
- LPV 是实时计算的,而不是预计算
VXGI
- Voxel Global Illumination (VXGI)
- two-pass 的算法
和 RSM 的区别
- RSM 的光源是每个像素表示的微小表面
- VXGI 将整个场景离散成很多个格子
- 例如八叉树的方式组织整个场景

- 渲染的时候从相机出发,对每个像素发出 eye ray,对于场景中碰到的点进行
cone tracing
- glossy 物体的反射叶是一个锥形的区域
具体步骤
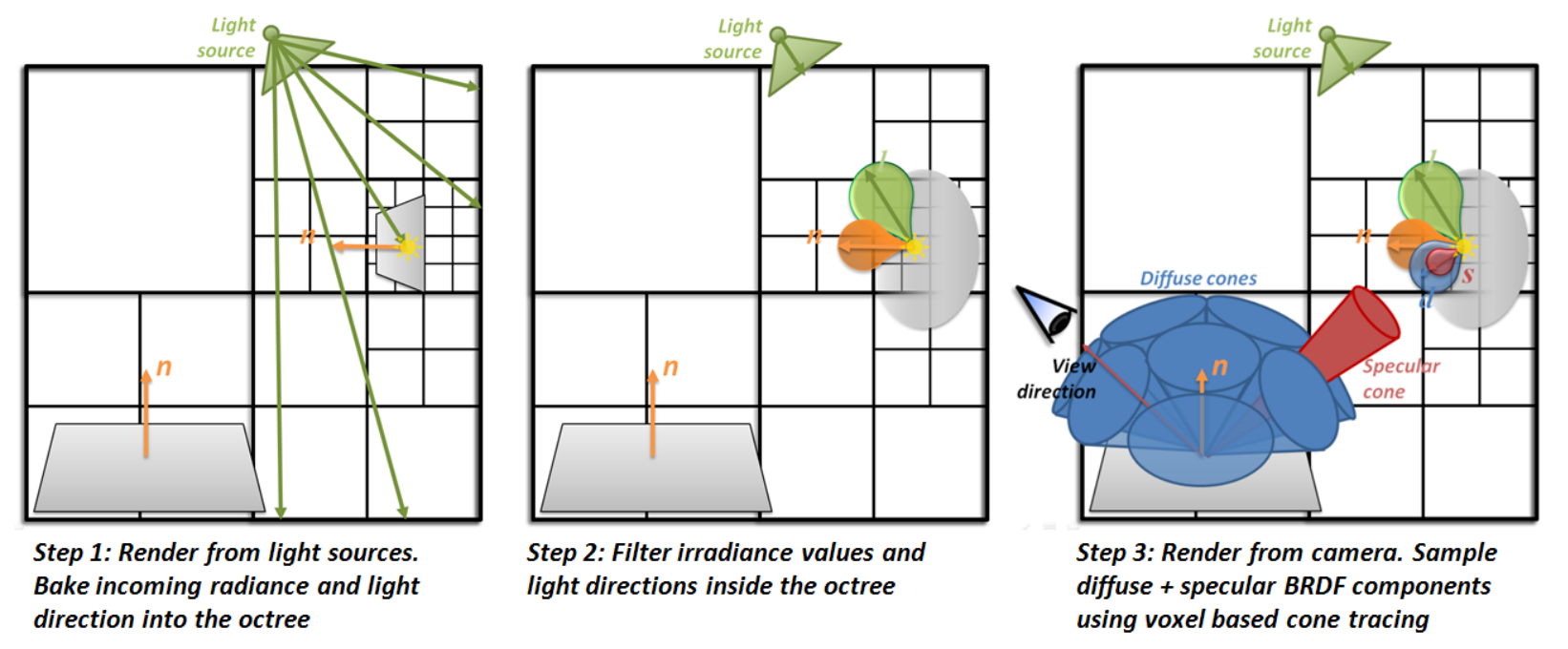
pass 1: from the light
- 首先我们需要对整个场景体素化,建立一个层次结构
- 需要在层次结构中更新
- 更多的情况,高层结构是将低层结构收集起来(合并)
- 在每1个体素中记录法线的分布、光源入射方向的分布
pass 2: from the camera
glossy 物体
- 对于 glossy 的物体,反射叶就是一个锥形
- 一种最简单的方法,从 shading point
连出一个圆锥,逐体素是否和圆锥相交,如果相交,则计算整个体素对于 shading
point 的贡献值
- 加速:圆锥的大小在传播过程中是越来越大的,因此我们可以通过距离估计出范围大小,然后在八叉树的对应层次结构中对应的一块即可
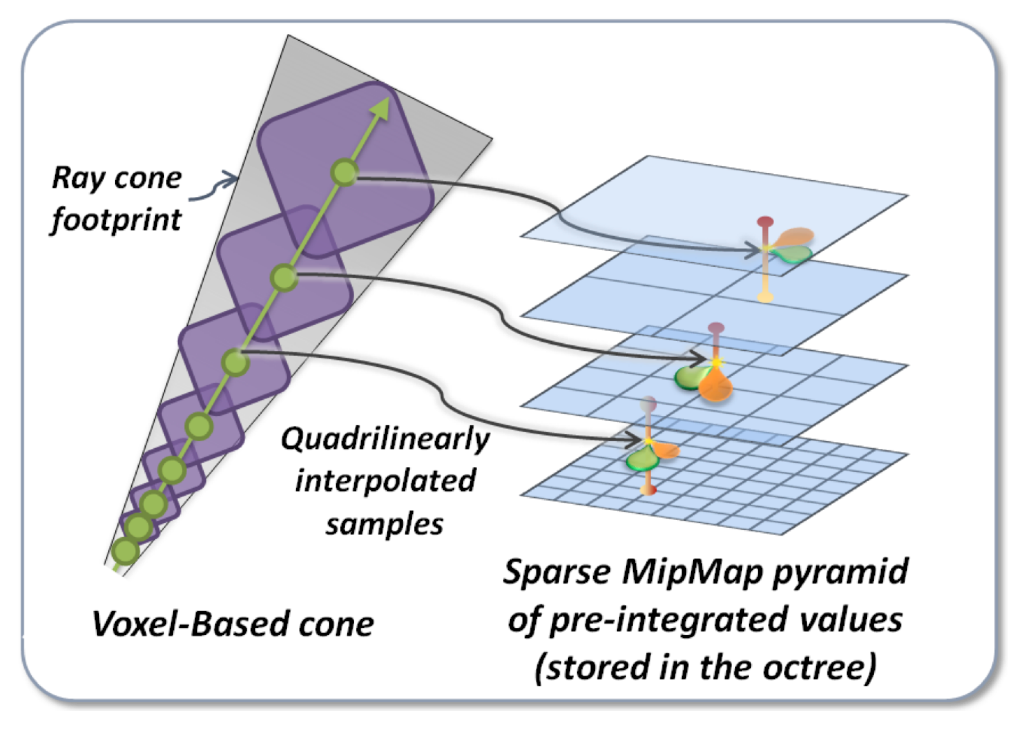
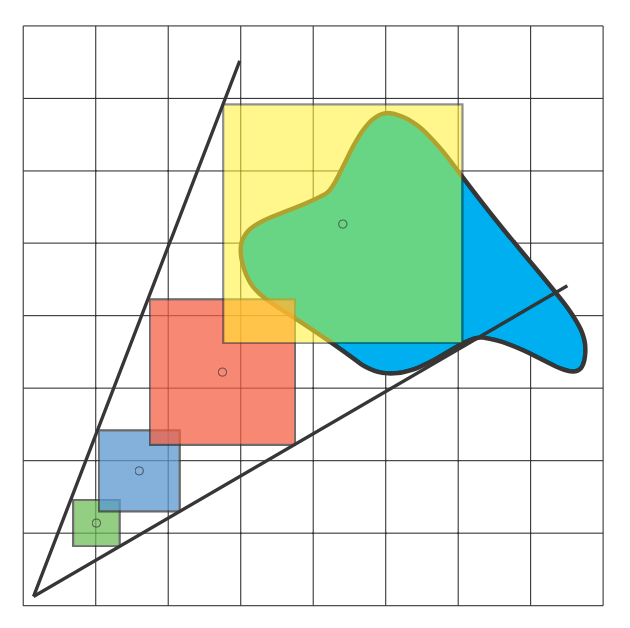
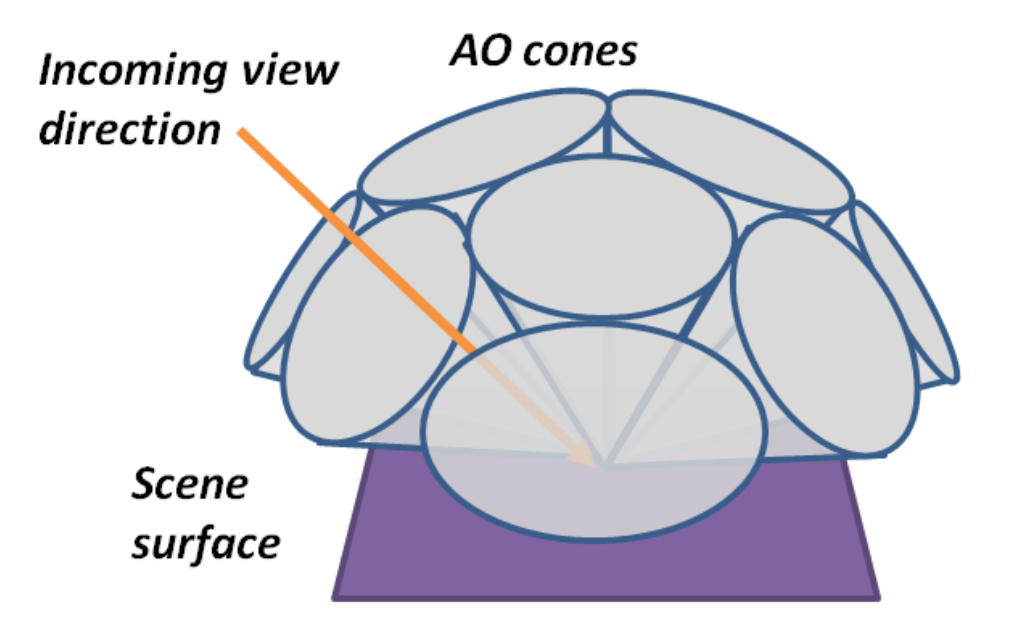
diffuse 物体
- 可以使用若干圆锥近似
- 圆锥之间有缝,但是这对于 diffuse 物体是可以接受的
评价
- 在当时的情况下,算是比较好的一种方法
- 很像我们在离线渲染中做的 photon mapping 的操作
- 存在一些他自己的问题
- 由于开销较大,应用比较少
- 场景的体素化是很麻烦的,可能需要预计算
- 对于动态场景而言更是如此,每一帧可能都得重建