GAMES202.闫令琪.06.实时环境光照(2)
- https://www.bilibili.com/video/BV1YK4y1T7yY
实时环境光照
- Precomputed Radiance Transfer
Shadow From Environment Lighting
- 怎么从环境光照中得到阴影
- 对于实时渲染而言,非常难
对环境光照的不同角度理解
多光源
- 可以把环境光理解为四面八方来的光照,理解为每个方向的都有光源
- 环境光照被描述为一个
many-light problem- 如果使用 SM 的话,每个光源需要一个 SM
- 代价很高
采样
- 可以通过采样估计,但是不知道 visibility 项(基于光栅化成像方法),采样很盲目
- 之前的不等式(约等式)拆分不容易(visibility
不能剥离开来),因为有环境光项的存在
- support 是整个半球
- 变化不一定 smooth
工业界的解决方案
- 只处理最亮的几个光源
- 环境光遮蔽(AO)
- 只能处理 constant environment lighting 情况下的光照
- 全白、全灰等
- 否则估计不准
- 只能处理 constant environment lighting 情况下的光照
相关研究
- Imperfect shadow maps
- 相对好懂
- Light cuts
- 反射物当作光源、光源归类
- RTRT (might be the ultimate solution)
- Real-Time Ray Tracing
- Precomputed radiance transfer
- 能够得到非常准确得到环境光的阴影
工业界
- 游戏引擎使用的方法和我们学的差不多,但是在实现上可能融合了很多种方法
- 工业界怎么实现的又快又好才是重点
频域与滤波
傅里叶变换
- 傅里叶变换 Foutier Transform
- 任意函数都可以展开为 sin/cos 函数的线性组合
- 基函数
- 频率高,变化快
- 图像主要是低频区域
- 高频区域是细节
- 滤波器:去除某些频率的内容,保留感兴趣的频率
- 时域卷积 \(\leftrightarrow\) 频域相乘
- 模糊
- 时域卷积
- 频域低通滤波(乘一个低通滤波器)
滤波的理解
- 乘积的积分可以理解为一种滤波
- Any product integral can be considered as filtering
\[ \int_{\Omega}f(x)g(x)dx \]
- 低频:smooth
- Low frequency == smooth function / slow changes / etc
- 上面积分得到的结果的频率是积分项中频率较低的一项
- 由较低的一项决定
- The frequency of the integral is the lowest of any individual’s
- 从频域上的相乘理解
基函数
- Basis Functions
- 一组线性无关的函数,任意函数都可以由这组函数线性表出
- A set of functions that can be used to represent other functions in general
- 基函数正交
- 傅里叶变换中的 \(\sin/\cos/\cdots\)
- 泰勒展开中的多项式 \(x/x^2/\cdots\)
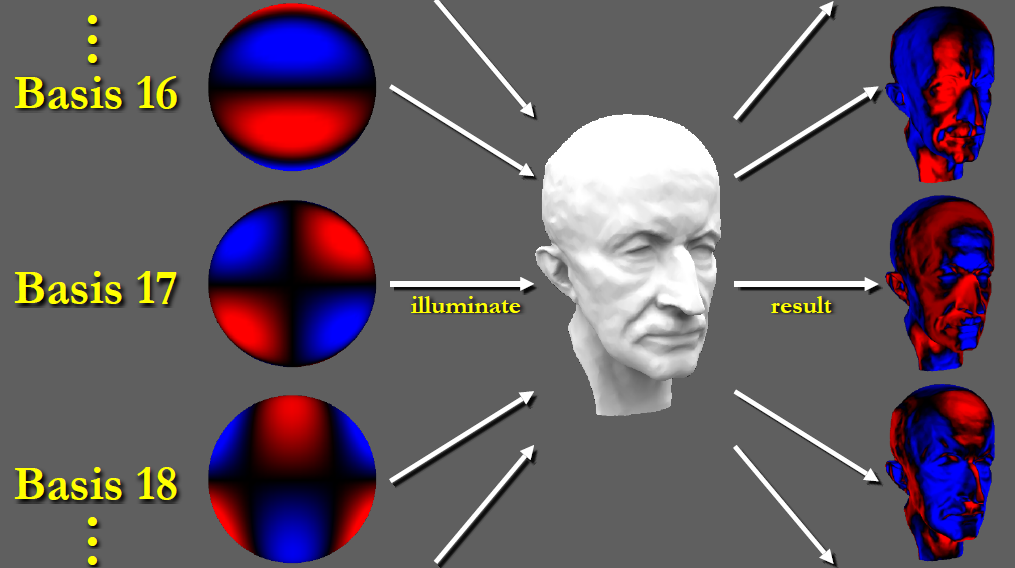
球面谐波函数
- Spherical Harmonics
- A set of 2D basis functions defined on the sphere
- 一系列的的二维函数,定义在球面上
- 方向函数 \((\theta,\phi)\)
- 球面谐波函数的可视化
- 每一行的频率是一样的,第 \(l\) 阶的 SH
- \(m=2l+1\)
- 前 \(n\) 阶一共有 \(n^2\) 个基函数
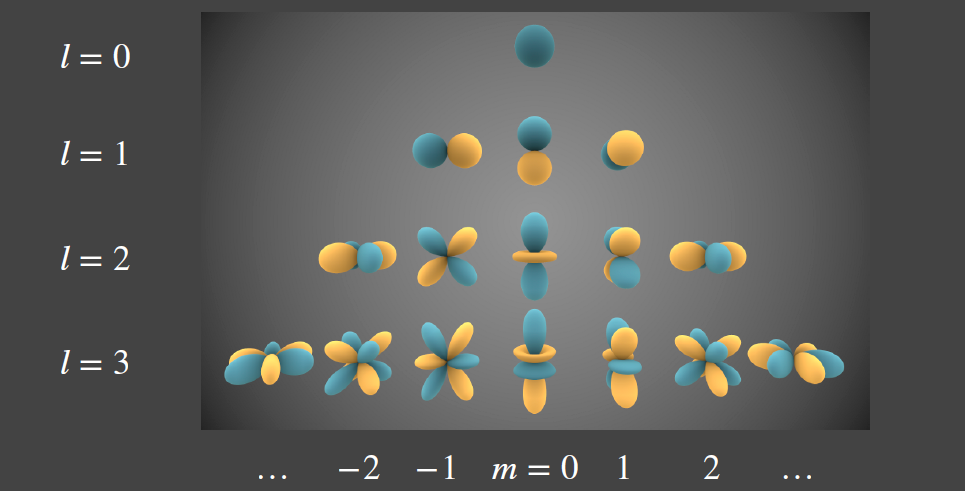
- 上图中
- 颜色表示值(白/黑)
- 值的变换快慢是频率
- 为什么不使用 2D 的傅里叶变换
- 不适合球面,可能最终会在球面上产生一条缝
- SH 定义在球面上,因此在球面上的变换更加 smooth
- 每一个基函数可以被勒让德多项式定义
- Each SH basis function \(B(\omega_i)\) is associated with a (Legendre) polynomial
- 投影操作
- 给定任意一个的定义在球面上的函数 \(f(w)\),其展开为 SH 表示的系数为
\[ c_i=\int_{\Omega}f(\omega)B_i(\omega_i)\mathrm{d}(\omega) \]
- 恢复函数的的时候,可以直接保留前几项(例如前 4 阶)
- 类似于傅里叶变换中保留前几项,就可以恢复出一个相对可以接受的结果
环境光照下 diffuse 物体的 shading
- 不考虑 shadow
- 上一节课:Prefiltering + single query = no filtering + multiple queries
- 我们的想法是通过i分析 diffuse 的 BDRF ,发现这是个低频成分,于是我们不需要保留光照太多的高频信息,于是我们可以指考虑光照在球面谐波函数中的前几项即可
分析 BRDF
- diffuse 物体的 BRDF
表现的效果就是一个低通滤波器(球面上)
- 相关,卷积
\[ E_{lm}=A_lL_{lm} \]
- \(A_l\) 为系数(\(l\) 为偶数)
\[ A_l=2\pi\dfrac{(-1)^{\frac{l}{2}-1}}{(l+2)(l-1)}\left[\dfrac{l!}{2^l(\frac{l}{2}!)^2}\right] \]
- 使用前 3 阶的 SH 就能够很好的恢复
- 因为 diffuse 的 BRDF 十分低频,最终得到的结果肯定也是低频项占据主导
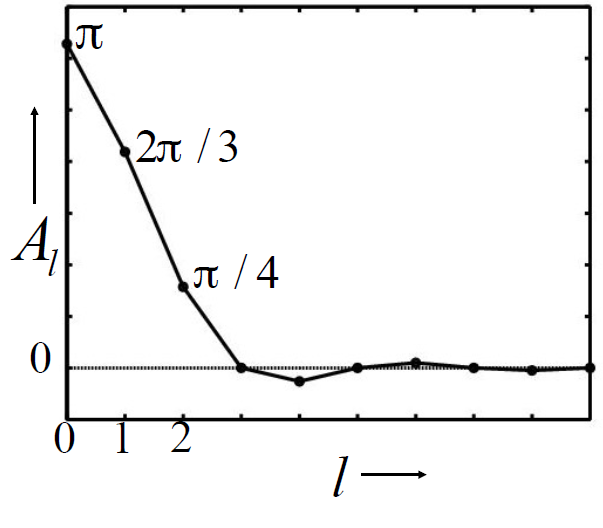
估计光照
- 因为 diffuse 的 BRDF 十分低频,最终能够得到的结果也会是一个低频信号
- 我们要计算的积分最终结果是 BRDF 和光照的卷积
- 没必要保留光照太多的高频信息
实验
- ground truth

- 使用前 1/2/3 阶的 SH 进行恢复光照,然后最终 shading 的结果
- RMS ERROR:25%,8%,1%

SH评价
- 很适合描述低频的 BRDF、低频的光照
Diego
- 两行代码获得博士学位
- 引入球谐函数,引领了一个时代

1 | surface float1 irradmat (matrix4 M, float3 v) { |
SH 的性质
- orthonormal
- 正交
- simple projection/reconstruction
- 投影/重建好算
- simple rotation
- 旋转球面上的任意函数,等价于旋转基函数
- 旋转基函数,新的基函数可以被同阶的其他基函数线性表出
- 因此旋转函数,相当于修改基函数的系数
- simple convolution
- few basis functions: low freqs
- 使用较小阶的基函数就能够得到不错的效果(低频)

PRT
- Precomputed Radiance Transfer
- 渲染方程
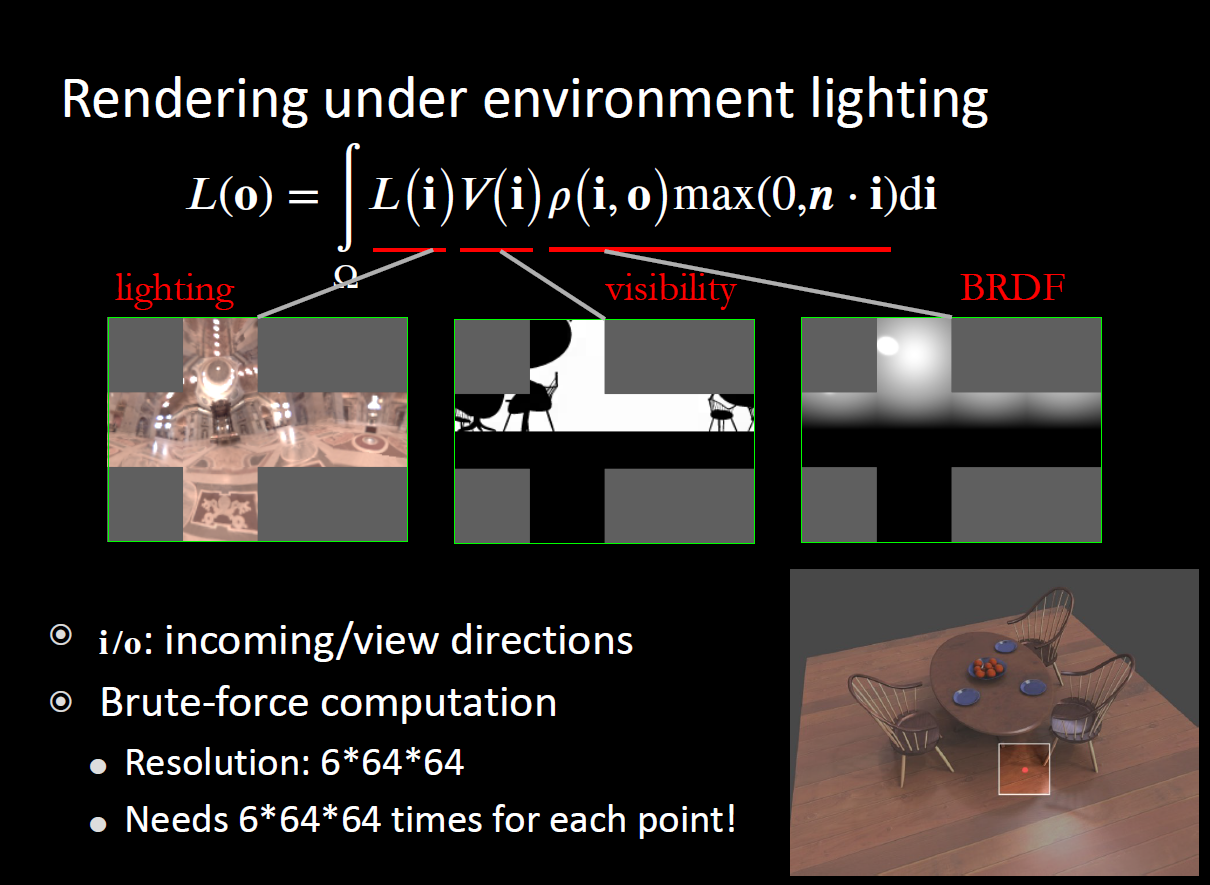
- 右下角中的红点对应的 3 张图
- 复杂度很高,对于每一个点,需要取遍 6 张贴图中的所有点
- \(6\ast64\ast64\)
PRT 论文
- Precomputed Radiance Transfer for Real-Time Rendering in Dynamic, Low-Frequency Lighting Environments [Sloan 02]
- SIGGRAPH 2002
- 利用球谐函数的性质进行预计算
- 用另一种角度看待渲染方程
- 我们假设场景是不变的,改变的只是光照
- 光照的位置、光照的颜色
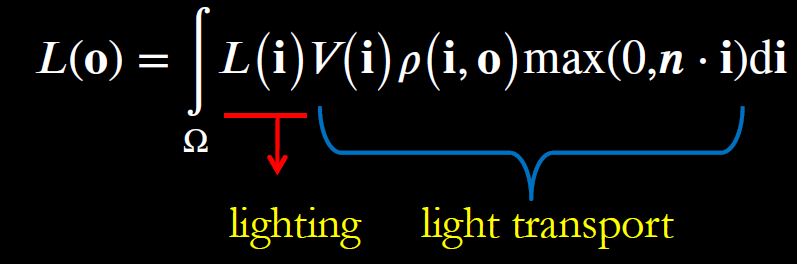
- 把 Lighting 表示为基函数
- 场景是不变的,因此在预计算的时候把 light transport 先计算出来,然后用基函数表示
PRT Diffuse 物体
- 将 diffuse 常数项从渲染方程中提取出来
\[ L(\boldsymbol{o})=\rho\int_{\Omega}L(\boldsymbol{i})V(\boldsymbol{i})\max(0,\boldsymbol{n}\cdot \boldsymbol{i})\mathrm{d}\boldsymbol{i} \]
- 光照使用 SH 表示
\[ L(\boldsymbol{i})\approx\sum l_iB_i(\boldsymbol{i}) \]
- 渲染方程变为
\[ L(\boldsymbol{o})=\rho\sum l_i{\color{red}\int_{\Omega}B_i(\boldsymbol{i})V(\boldsymbol{i})\max(0,\boldsymbol{n}\cdot \boldsymbol{i})\mathrm{d}\boldsymbol{i}} \]
- 红色部分与光照无关,可以预计算,记作 \(T_i\),渲染方程变为
- 预计算的话不考虑时间
- Reduce rendering computation to dot product
\[ L(\boldsymbol{o})=\rho\sum l_iT_i \]
- 场景是不能动的,因为动了,visibility 项就变了,预计算失效
- 能不能解决光源移动的问题?
- 可以,SH 的性质,如果光源做了一个旋转操作,很快就能够得到新的 SH
PRT 另外一种预计算的方式
- 渲染方程
\[ L_o(p,\omega_o)= \int_{\Omega^+}{\color{red}L_i(p,\omega_i)}{\color{blue}f_r(p,\omega_i,\omega_o)\cos\theta_i V(p,\omega_i)}d\omega_i=\int_{\Omega^+}{\color{red}L(\omega_i)}{\color{blue}T(\omega_i)}d\omega_i \]
- 把 lighting 和 light transport 都用基函数表示出来
\[ L(\omega_i)\approx\sum_{p}c_pB_p(\omega_i) \]
\[ T(\omega_i)\approx\sum_{q}t_qB_q(\omega_i) \]
- 重新表示渲染方程
\[ L_o(p,\omega_o)=\sum_{p}\sum_{q}c_pt_q\int_{\Omega^+}B_p(\omega_i)B_q(\omega_i)d\omega_i \]
- 似乎看起来是 \(O(n^2)\) 的,但是由于 SH 的正交性,只有 \(p=q\) 的情况下才不为 0
PRT Glossy 物体
- diffuse 物体,BRDF 为常数
- glossy 物体,4D 的 BRDF
- 和 diffuse 的区别,上面 light transport(蓝色项)还与方向矢量 \(o\) 有关(与视点有关)
- 因此就算是使用了基函数,结果还是和 \(o\) 相关
\[ L(o)\approx\sum_{i} l_iT_i(o) \]
- 能否将 \(T_i(o)\) 也用基函数表示
\[ T_i(o)\approx\sum_{j} t_{ij}B_j(o) \]
\[ L(o)\approx\sum_{i}\sum_{j} l_it_{ij}B_j(o) \]
- 这样看来,我们需要把 light transport 作为一个矩阵来看待(而不是之前的向量)

- 存储开销变大了,计算开销也变大了
- SH 阶数
- diffuse 使用 3 阶 SH 就够了
- glossy 需要一些高频成分,4 阶或者 5 阶
- 非常高频,接近镜面的物体,PRT 无法解决
- 需要很高阶,而且效果不好
- 可以直接采样
Interreflection and caustics
- 光路 transport paths
- \(LE\)(直接看到光源)
- light - eye
- \(LGE\)(直接反射)
- light - glossy - eye
- \(L(D|G)\ast E\)
- \(LS\ast(D|G)\ast E\)
- caustics
- \(LE\)(直接看到光源)
- PRT 在做完预计算之后,实际渲染的过程复杂度和 transport 的复杂度是无关的
- 也就是说 PRT 可以模拟任意复杂的 transport
怎么进行预计算
- 基函数看作是光照
- 对于 diffuse 物体
\[ T_i=\int_{\Omega}B_i(\boldsymbol{i})V(\boldsymbol{i})\max(0,\boldsymbol{n}\cdot \boldsymbol{i})\mathrm{d}\boldsymbol{i} \]
- 形式上还是和 rendering equation,因此可以把基函数看作是某种光照
- 因此,预计算的过程可以看作是一个离线渲染的过程,具体方法可以用之前提到的其他算法
PRT 的问题
- 不太适用于高频的光照(需要用很多的高阶的基函数)
- 要求场景是固定的
- 材质也需要是固定的
- 存储开销
PRT 的改进
- More basis functions
- 其他的基函数
- dot product => triple products
- 预计算更多的部分,例如 BRDF、visibility 等
- Static scene => dynamic scene
- Fix material => dynamic material
- Other effects: translucent, hair, ...
- Precomputation => analytic computation
- 解析解,例如 split sum
其他的一些基函数
- Spherical Harmonics (SH)
- Wavelet
- Zonal Harmonics
- Spherical Gaussian (SG)
- Piecewise Constant
小波
- Wavelet
- 有很多种
- 2D Haar Wavelet
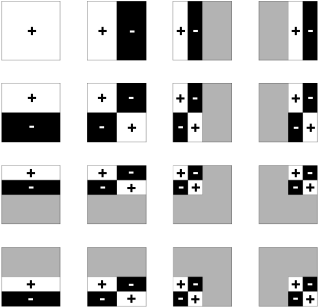
- 小波定义在图像块上的,不同的小波定义域也不相同
- 灰色部分就是没有定义的地方
- 小波变换之后,很多基函数对应的系数为 0
- 保留最大的多少个不为 0 的项即可
- 非线性估计
- 对全频率的表示
- 由于小波是定义在平面上的,因此我们使用 cube map 去表示环境光照
- 对每个面进行小波变换
- 将系数最大的几个项存在右上、右下、左下部分,对剩余的部分继续进行小波变换

- JPEG 文件使用了 DCT(离散余弦变换)去进行图像压缩
- 和小波变换比较像
小波 vs 球谐

- 小波变换
- 保留了一些高频信息,产生很多高频阴影
- 不支持快速旋转光照