数据库概论.陈立军.03.关系模型(3)

Posted on Edited on In Views:
包、作为约束语言的关系代数、全关系系统、关系数据库12条准则、元组关系演算、域关系演算

关系模型

包

  • bag
  • 允许重复的集合，或者称为多集（multi-set）
  • 引入包的原因
    • 效率，不用去重
    • 合理地计算聚集函数的值

包的关系代数运算

包的选择、投影、笛卡尔积

  • 和集合上定义是一样的，只需保留重复即可

包的并、交、差

  • 假定一个元组 \(t\) 在包 \(R\) 中重复出现了 \(n\) 次，在包 \(S\) 中重复出现了 \(m\) 次
    • 在 \(R\cup S\) 中，\(t\) 出现 \(n+m\) 次
    • 在 \(R-S\) 中，\(t\) 出现 \(\max\{n-m,0\}\) 次
    • 在 \(R\cap S\) 中，\(t\) 出现 \(\min\{n,m\}\) 次

包的关系代数运算律

  • 以下的运算律集合运算都满足，但是包运算只满足前4条

    • \((R\cup S)\cup T=R\cup(S\cup T)\)

    • \((R\cap S)\cap T=R\cap(S\cap T)\)

    • \(R\cup(S\cap T)=(R\cup S)\cap(R\cup T)\)

    • \(\sigma_{A\land B}(R)=\sigma_{A}(R)\cap \sigma_{B}(R)\)

      • 选择

    • \((R\cap S)-T=R\cap(S-T)\)

      • 反例：\(R=\{1,1\},S=\{1,1,1\},T=\{1\}\)
      • \(\{1\}\ne\{1,1\}\)

    • \(R\cap(S\cup T)=(R\cap S)\cup(R\cap T)\)

      • 反例：\(R=\{1\},S=\{1\},T=\{1\}\)
      • \(\{1\}\ne\{1,1\}\)

    • \(\sigma_{A\lor B}(R)=\sigma_{A}(R)\cup \sigma_{B}(R)\)

      • 反例：\(A=\{t|t.a=1\},B\{t|t.b=1\}\)，下图
      • \(\{x,y,z\}\ne\{x,y,y,z\}\)
      ID a b
      x 1 2
      y 1 1
      z 2 1

作为约束语言的关系代数

约束

  • 关系代数表达约束的形式
    • \(R=\phi\) 或者 \(R\subseteq S\)
  • \(R=\phi\)：声明不满足条件的关系代数为 \(R\) ，令 \(R\) 为空集
  • \(R\subseteq S\)

例子

  • 参照完整性
  • \(R(A,B),S(B,C),S\) 中的 \(B\) 是参照 \(R\) 的 \(B\) 的外码
  • \(\prod_{B}(S)\subseteq\prod_{B}(A)\)

函数依赖

  • \(R(A,B)\) 要求在 \(A\)上相等的在 \(B\) 上也相等
  • 通过反面来表达
  • \(\sigma_{R.A=S.A\land R.B\ne S.B}\left(R\times \rho_S(R)\right)=\phi\)

思考

  • \(R(A,B)\) 如何确定 \(A\) 的唯一性（列 \(A\) 上的取值都不相同）
    • 只有两个属性 \(A,B\)，而且是对集合而言
    • 表达式和上面函数依赖的结果是相同的
  • \(R(A,B,C)\) 如何确定 \(A\) 的唯一性（列 \(A\) 上的取值都不相同）
    • 有三个属性 \(A,B,C\)，而且是对集合而言
    • \(\sigma_{R.A=S.A\land (R.B\ne S.B\lor R.C\ne S.C)}\left(R\times \rho_S(R)\right)=\phi\)

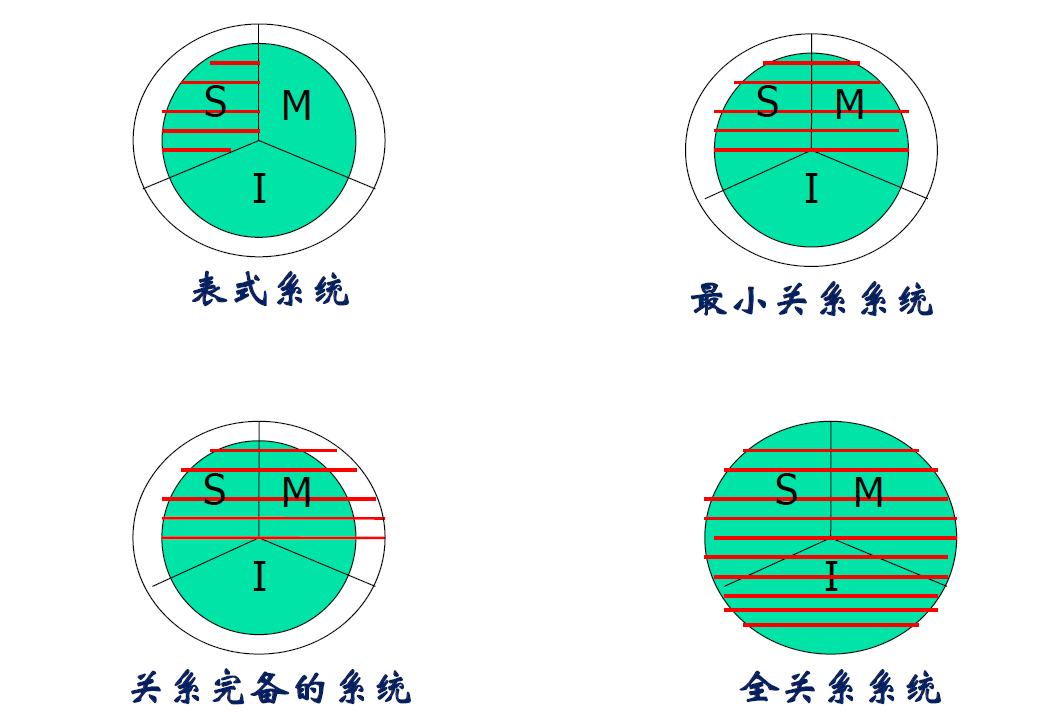
全关系系统

系统对关系的支持能力

  • 表式系统
    • 仅支持关系（即表）数据结构，不支持集合级操作
    • 表式系统不能算关系系统
  • 最小关系系统
    • 仅支持关系数据结构和三种关系搡作（选择、投影、链接）
      • 三种关系操作可以支持大部分的操作
    • 许多微机关系数据库系统如 FoxPro 属于此类
  • 完备关系系统
    • 支持关系数据结构和所有的关系代数操作
    • 90年代初的许多关系数据库管理系统属于这一类
  • 全关系系统
    • 这类系统支持关系模型的所有特征

表示（粗略表示）

  • S：数据模型
  • M：数据操作
  • I：数据完整性

全关系系统的十二条准则

准则 0

  • 一个关系型的 DBMS 必须能完全通过它的关系能力来管理数据库
    • 所有功能的实现必须在关系的层面来体现

准则 1：信息准则

  • 关系型 DBMS 的所有信息都应在逻辑一级上用一种方法即表中的值显式地表示
    • 所有的信息都必须保存在关系表里面
      • 业务表
      • 数据字典/元数据（表结构的定义）
      • 安全性、完整性条件的声明
    • 所有信息都得用关系表达

准则 2：保证访问准则

  • 依靠表名、主码和列名的组合，保证能以逻辑方式访问关系数据库中的每个数据项（分量值） 以关联寻址代替面向机器的访问方式
  • 所有的操作都必须是集合层面的

准则 3：空值的系统化处理

  • 全关系型 DBMS 应支持空值概念，并用系统化的方式处理空值
    • 空值的定义和检测都在系统层面实现
    • 如果系统不支持控制，都需要应用检测
      • 例如特殊字符（问题：特殊字符不够特殊）

准则 4：基于关系模型的动态的联机数据字典

  • 数据库的描述在逻辑级上应该和普通数据采用同样的表示方式，使得授权用户可以使用查询一般数据所用的关系语言来查询数据库的描述信息
    • 数据字典（元数据）也应该一关系表的形式存储在数据库中
    • 自描述、自复制代码

准则 5：统一的数据子语言

  • 一个关系系统可以有几种语言和多种终端使用方式（如QBE、嵌入式SQL），但必须有一种语言，它的语句可以表示为具有严格语法规定的字符串
    • 前端界面可以是各种操作，但是在系统内部必须有一种严格的关于数据操作的语言

准则 6：视图更新准则

  • 所有理论上可更新的视图也应该由系统更新，即对视图的更新要求，存在一个算法可以无二义地把更新要求转换为对基本表的更新序列
    • 视图，在关系表的基础上生成的虚拟表
  • 一个例子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/* 原始关系表 */
create table student(
    snochar(10) primary key,
    name char(10) unique,
    age int
)

/* 创建视图 */
create view student_info as (
    select name, age from student
)

/**
 * 不是理论上可更新的视图, 因为不包含主键, 而主键不能为空
 */
insert into student_infovalues (‘tom’, 20)

/**
 * 是理论上可更新的视图
 * 因为 name 加了 unique 关键字
 */
update student_info set age = 20 where name='jerry'
  • 具体分析是否语义上可更新很难
  • 现在实际的数据库在这点上做了权衡
    • 仅支持部分的更新（符合某种定义形式的视图）
    • 例如要求视图必须是行列子集的（通过选择、投影得到的结果）、还要包括原表的主码、不能包括聚集函数（min/max）

准则 7：高级的插入、删除和修改操作

  • 关系系统的操作对象是单一的关系
    • 都应该在关系层面上定义

准则 8：数据物理独立性

  • 无论数据库的数据在存储表示和存取方法上作任何变化，应用程序和终端活动都保持逻辑上的不变性

准则 9：数据逻辑独立性

  • 当对基本关系进行理论上信息不受损害的任何改变时，应用程序和终端活动都保持逻辑上的不变性

准则 10：数据完整性的独立性

  • 关系数据库的完整性约束条件必须是用数据库语言定义并存储在数据字典中的，而不是由应用程序加以定义
    • 系统支持数据完整性的检查，用户不需要自己做数据完整性的检查

准则 11：分布独立性

  • 分布独立性是指 DBMS 具有这样的数据库语言，使得应用程序和终端活动在下列情况下都保持逻辑上的不变性：
    • 在第一次引入分布式数据时，即如果原来的DBMS只管理非分布式的数据，而现在引入了分布式数据
    • 当数据重新分布时，即如果原来DBMS能管理分布式数据，现在要改变原来的数据分布
  • 分布的透明性，用户感觉不到分布式系统

准则 12：无破坏准则

  • 如果一个关系系统具有一个低级（一次一记录）语言，则这个低级语言不能违背或绕过完整性准则
    • 为获得完整性的独立性，需要让完整性约束条件和数据的逻辑结构相独立
    • 不能旁路（bypass）或者关闭约束检查子系统

元组关系演算

  • 形式化定义：\(\{t|P(t)\}\)
    • 表示所有使谓词 \(P\) 为真的元组集合
  • \(t\) 为元组变量
    • 如果元组变量前有“全称”（\(\forall\)）或“存在”（\(\exists\)）量词，则称其为约束变量，否则称为自由变量
  • \(P\) 是公式，由原子公式和运算符组成

原子公式

  • \(s\in R\)
    • \(s\) 是关系 \(R\) 中的一个元组
  • \(s[X]\ \theta\ u[Y]\)
    • \(s[X]\) 与 \(u[Y]\) 为元组分量，它们之间满足比较关系 \(\theta\)
  • \(s[X]\ \theta\ c\)
    • 分量 \(s[X]\) 与常量 \(c\) 之间满足比较关系 \(\theta\)

公式的递归定义

  • 原子公式是公式
  • 若 \(P\) 是公式，则 \(\neg P\) 也是公式
  • 若 \(P_1,P_2\) 是公式，则 \(P_1\land P_2,P_1\lor P_2,P_1\Rightarrow P_2\) 也是公式
  • 若 \(P(t)\) 是公式，\(R\) 是关系，则 \(\forall t\in R\left(P(t)\right),\forall t\in R\left(P(t)\right)\) 也是公式

元组关系演算示例

公式的等价性

  • \(P_1\land P_2 \Leftrightarrow \neg(\neg P_1\lor\neg P_2)\)
  • \(\forall t\in R(P(t)) \Leftrightarrow \neg \exists t\in R(\neg P(t))\)
  • \(P_1\Rightarrow P_2 \Leftrightarrow \neg P_1\lor P_2\)

关系演算表达式的安全性

  • 元组关系演算有可能会产生无限关系，这样的表达式是不安全的
  • 如 \(\{t| \neg(t\in R)\}\)，求所有不在 \(R\) 中的元组
  • 引入公式 \(P\) 的域概念，用 \(dom(P)\) 表示
    • \(dom(P)=\) 显式出现在 \(P\) 中的值 + 在 \(P\) 中出现的关系的元组中出现的值（不必是最小集）
    • 如定义 \(dom(\{t| \neg(t\in R)\})\) = \(\{R\) 中出现的所有值的集合 \(\}\)
  • 如果出现在表达式 \(\{t|P(t)\}\) 结果中的所有值均来自 \(dom(P)\)，则称 \(\{t|P(t)\}\) 是安全的

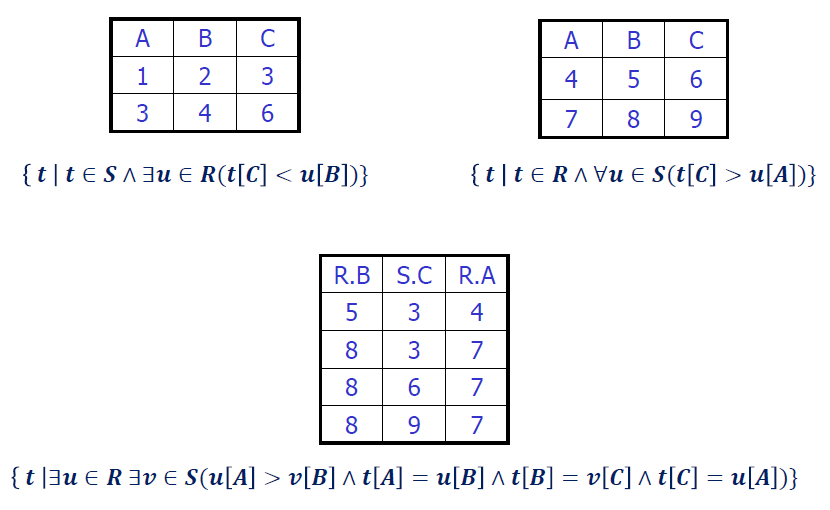
元组关系演算查询示例

  • 区分找老师、找老师姓名（加一个投影）

  • 先选择，再投影

元组关系演算与关系代数的等价性

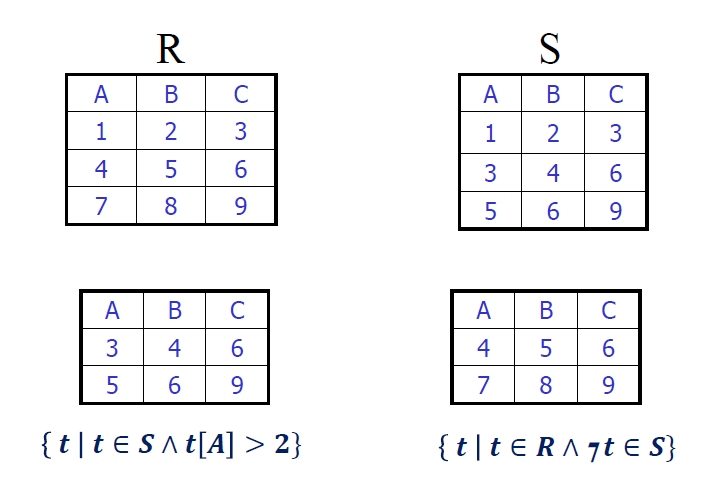
域关系演算

  • 形式化定义
    • \(\left\{<x_1,\cdots,x_n>|P(x_1,\cdots,x_n)\right\}\)
    • \(x_i\) 代表域变量，\(P\) 为由原子构成的公式
  • 原子公式
    • \(<x_1,\cdots,x_n>\in R\)：\(x_i\) 是域变量或域常量
    • \(x\ \theta\ y\)：域变量 \(x\) 与 \(y\) 满足比较关系 \(\theta\)
    • \(x\ \theta\ c\)：域变量 \(x\) 与常量 \(c\) 满足比较关系 \(\theta\)

域关系演算例子