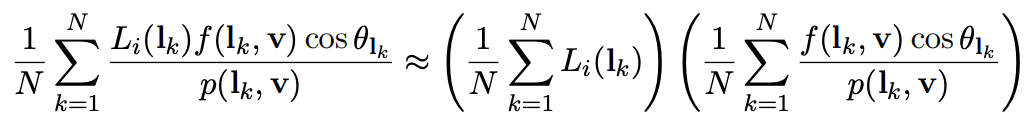GAMES202.闫令琪.05.实时环境光照(1)

Posted on Edited on In Views:
IBL、The Split Sum Approximation
  • https://www.bilibili.com/video/BV1YK4y1T7yY

实时环境光照

  • Real-Time Environment Mapping

Shading from Environment Lighting

  • 环境光照下任意点的 shading（不考虑阴影）
  • 环境光照
    • 一张贴图
    • 记录了各个方向上来自于无限远的光照
  • 典型的保存方式：cube map，spherical map
  • 怎么使用环境光照来渲染一个物体
    • IBL：Image-Based Lighting
  • 不考虑可见性（阴影），渲染方程如下

\[ L_o(p,\omega_o)= \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_id\omega_i \]

  • 蒙特卡洛积分可以求解上面的渲染方程
    • 通常而言，基于 sampling 的方法在实时渲染不太适用（比较慢）
    • 但是现在技术进步允许 sampling 的方法应用了
  • 接下来的方法就是使用预计算代替采样

The Split Sum Approximation

近似方案

  • 基于如下的观察
    • glossy 材质：small support
    • diffuse 材质：smooth

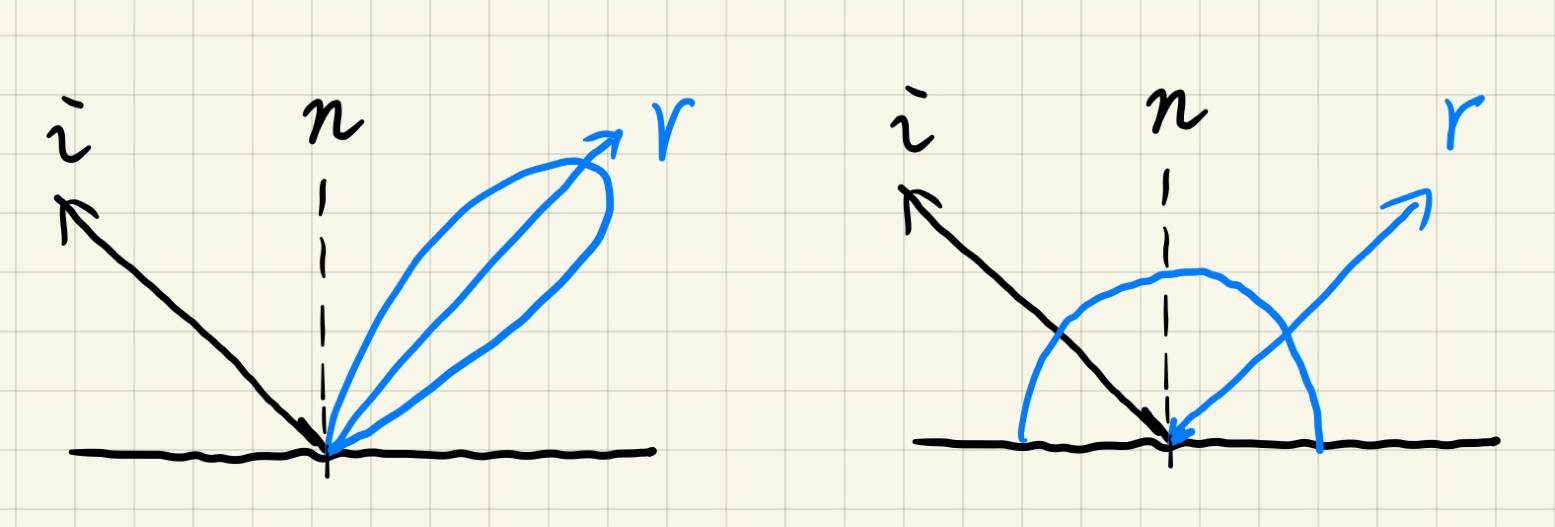
  • 使用之前的近似方案
    • 一点点小的区别，我们只需要对 BRDF 覆盖的范围 \(\Omega_G\) 进行积分即可

\[ \int_\Omega f(x)g(x)dx\approx \dfrac{\int_{\Omega_G} f(x)dx}{\int_{\Omega_G} dx}\cdot {\int_\Omega g(x)dx} \]

\[ L_o(p,\omega_o)= {\color{red}\dfrac{\int_{\Omega_{G_{f_r}}} L_i(p,\omega_i)d\omega_i}{\int_{\Omega_{G_{f_r}}} d\omega_i}} {\color{blue}\int_{\Omega^+}f_r(p,\omega_i,\omega_o)\cos\theta_id\omega_i} \]

  • 分为两个部分之后，分别计算

1st Stage

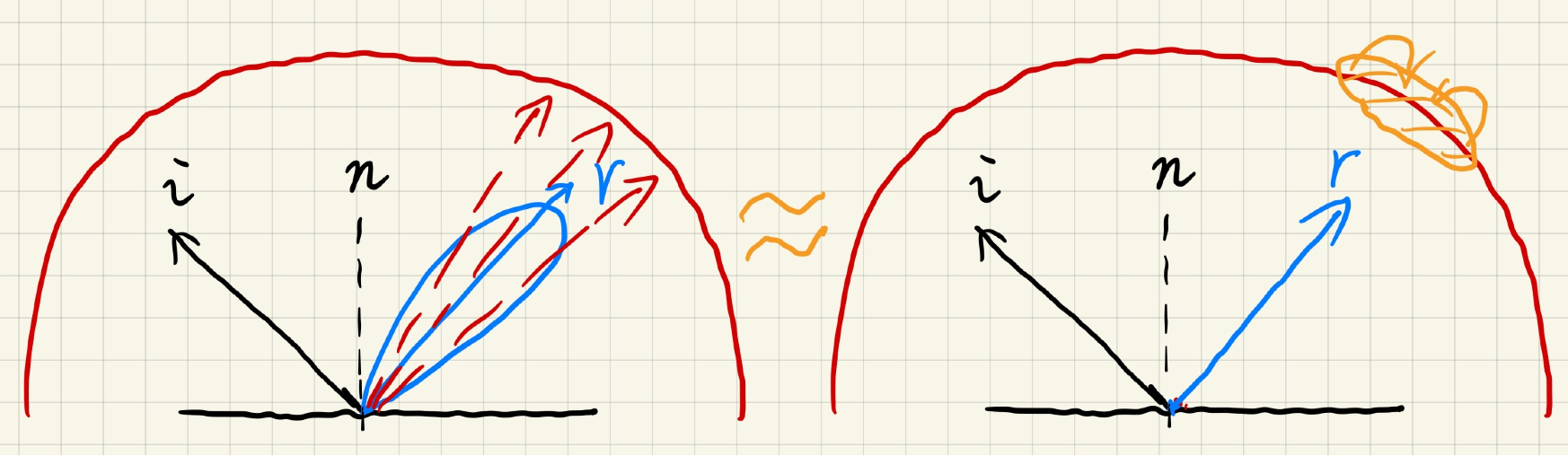
  • 第一部分的积分
  • 红色区域就是对光源的入射方向（上面的 r ）进行了一个滤波
  • prefilter，在 rendering 之前预先处理
    • 类似于 MIPMAP 的思想
    • 预先生成多张使用不同滤波核 filter 的环境贴图
    • 之后在 shading 的时候进行一个查询，双线性插值
    • 如果查询的值不是一个预先设置的滤波核的大小，三线性插值

  • 如果是球面环境贴图，需要保证整个 filter 是在球面上发生的
  • 求积分 vs prefilter

2nd Stage

参数维度：5

  • 第二部分的积分
  • 蓝色部分的积分
  • 预先计算 precompute
  • 假定是 microfacet 的 BRDF
    • 只需要知道菲涅尔项、微表面的法线分布（roughness）
      • Precompute its value for all possible combinations of variables roughness, color (Fresnel term), etc.
    • 还是很难求积分
    • 而且保存结果需要很大的内存（至少5D 的表）
    • roughness（一个数）、菲涅尔项（rgb 3 通道、入射角）

参数维度：3

  • 微表面模型的BRDF
    • 只考虑菲涅尔项和微表面的法线分布就行
    • 菲涅尔项：决定颜色
    • 微表面的法向分布：材质（glossy、diffuse）

\[ f(\mathbf{i}, \mathbf{o})=\frac{\mathbf{F}(\mathbf{i}, \mathbf{h}) \mathbf{G}(\mathbf{i}, \mathbf{o}, \mathbf{h}) \mathbf{D}(\mathbf{h})}{4(\mathbf{n}, \mathbf{i})(\mathbf{n}, \mathbf{o})} \]

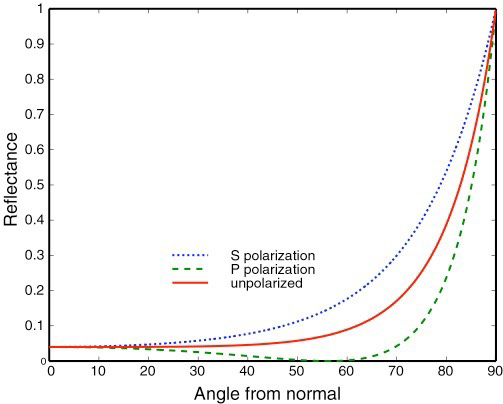
  • 菲涅尔项可以用一个函数近似
    • Schlick’s approximation
    • 认为不同的材质是两个参数的函数：入射光夹角、基础反射率（基础颜色）

\[ R(\theta) =R_{0}+\left(1-R_{0}\right)(1-\cos \theta)^{5} \]

\[ R_{0} =\left(\frac{n_{1}-n_{2}}{n_{1}+n_{2}}\right)^{2} \]

  • 可以定义一个法线分布
    • Beckmann distribution
    • \(\alpha\) 定义 roughness，分布的胖瘦
    • \(\theta_h\) 表示法线和半角矢量的夹角
      • 半角矢量和入射方向是可以互相转换的

\[ D(h)=\dfrac{e^{-\dfrac{\tan^2\theta_h}{\alpha^2}}}{\pi\alpha^2\cos^4\theta_h} \]

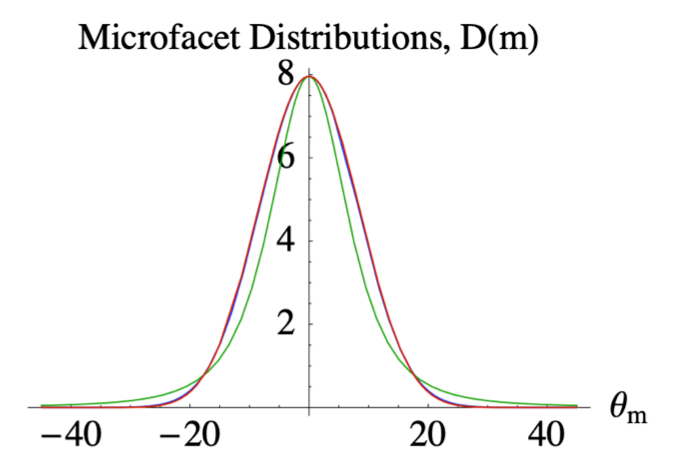
  • 所以说现在预计算只需要保存 3D 的图（参数维度是 3D ）
    • 认为 \(R_0\) 是灰度

参数维度：2

  • 怎么继续降维
  • 显式把上面的菲涅尔项写进去，试图把 \(R_0\) 分离开来
    • 分母的 \(F\) 会被消掉
    • \(f_r=FD\)

\[ \int_{\Omega^+}f_r(p,\omega_i,\omega_o)\cos\theta_id\omega_i \]

\[ \approx\ R_0\int_{\Omega^+}\dfrac{f_r}{F}(1-(1-\cos \theta)^{5})\cos\theta_id\omega_i+\int_{\Omega^+}\dfrac{f_r}{F}(1-\cos \theta)^{5}\cos\theta_id\omega_i\\ \]

  • 积分的维度变成了 2D
  • 直接打表 2D

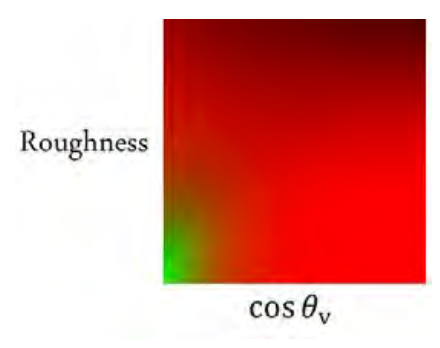
  • 在实现的时候甚至可以使用一张纹理的两个通道

评价

  • 避免了采样
  • 很快，效果很好

实时渲染应用

  • 使用求和代替积分（说的同一件事）