GAMES202.闫令琪.04.实时阴影(2)
- https://www.bilibili.com/video/BV1YK4y1T7yY
实时阴影
PCF/PCSS
背后的数学
PCF
- filter/convolution
- 卷积
\[ [w\ast f](p)=\sum_{q\in \mathcal{N}(p)}w(p,q)f(q) \]
PCSS
\[ V(x)=\sum_{q\in \mathcal{N}(p)}w(p,q)\cdot\chi^+[D_{SM}(q)-D_{scene}(x)] \]
- \(\chi^+(x)\)
- \(1,x\ge0\)
- \(0,x<0\)
- PCF 并不是对 SM 进行模糊
\[ V(x)\ne\chi^+\{[w\ast D_{SM}](x)-D_{scene}(x)\} \]
- PCF 也不是在图像空间(结果图)上做 filter
- 二值的结果图(也就是经典 SM 做出来的阴影效果)
\[ V(x)\ne \sum_{y\in\mathcal{N}(x)}w(x,y)V(y) \]
PCSS 的步骤
- Step 1: Blocker search
- 在某个区域内计算平均遮挡深度
- Step 2: Penumbra estimation
- 通过计算出来的平均遮挡深度来计算半影(penumbra)的大小
- Step 3: Percentage Closer Filtering
- 根据 Step 2 计算出来的大小进行 PCF
限速步
- Step 1,Step 3
- 采样会比较慢
- Softer -> larger filtering region -> slower
- 两种方式
- 对区域内的每一个像素采样
- 对区域内的像素进行随机采样
- 稀疏采样会引起噪声
- 处理噪声的方法:图像空间降噪,时间维度降噪
- 低通滤波回式低频噪声通过,帧间闪烁现象变成 boiling artifact(沸腾的现象)
- flicker:如果每一帧取得随机数不一样,会引起帧间闪烁的问题
- 针对很慢的方法,提出了 Variance Shadow Mapping
VSSM / VSM
- Variance Soft Shadow Mapping
- 针对性地解决 PCSS 在第一步、第三步慢的问题
PCF 步骤(Step 3)
- 假设均值滤波
- 等价于想要知道在指定范围内有百分之多少的 texel 是在 shading point 之前
- 等价于在指定范围内找出有多少的 texel 深度值比 shading point 要小
- 等价于想知道当前像素在指定范围内,深度排到第几(百分之几)
- 如果知道指定区域的分布,那么就容易得到结果
- 如果不需要那么准确,知道直方图也能得到结果
- 假定是正态分布,也能得到结果(相对更加不准)
- 怎么定义一个正态分布:均值、方差
key idea
- 快速求出某个区域内的均值和方差
- mean + variance
均值
- MipMap:不准确,只能求正方形
- Summed Area Tables(SAT)
方差
\[ Var(X)=E(X^2)-E^2(X) \]
- 计算两个均值即可
- 存两张图
- 怎么在 OpenGL 中实现
- 4 通道,一个通道存 \(SM\ (depth)\),一个通道保存 \(SM^2\ (depth^2)\)
计算百分之几
- CDF:求出阴影面积
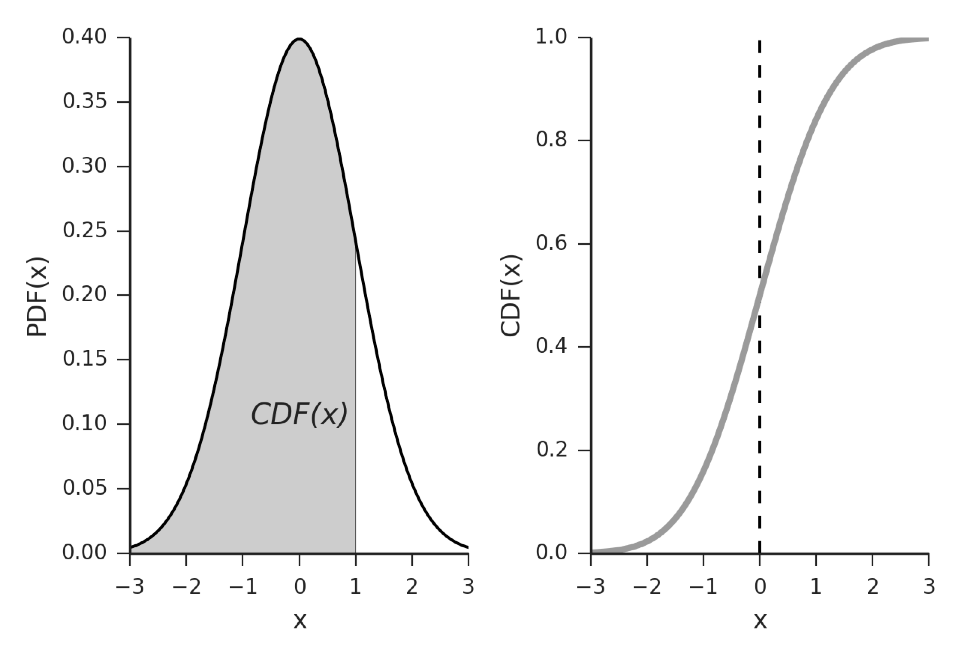
- 具体实现求积分:打表
- 误差函数:error function
- c++ 中有函数
erf()- 有数值解,没有解析解
切比雪夫不等式估计
- Chebychev’s inequality
\[ P(x>t)\le\dfrac{\sigma^2}{\sigma^2+(t-\mu)^2} \]
- 背后假设是单峰的分布
- 具体得去看证明过程
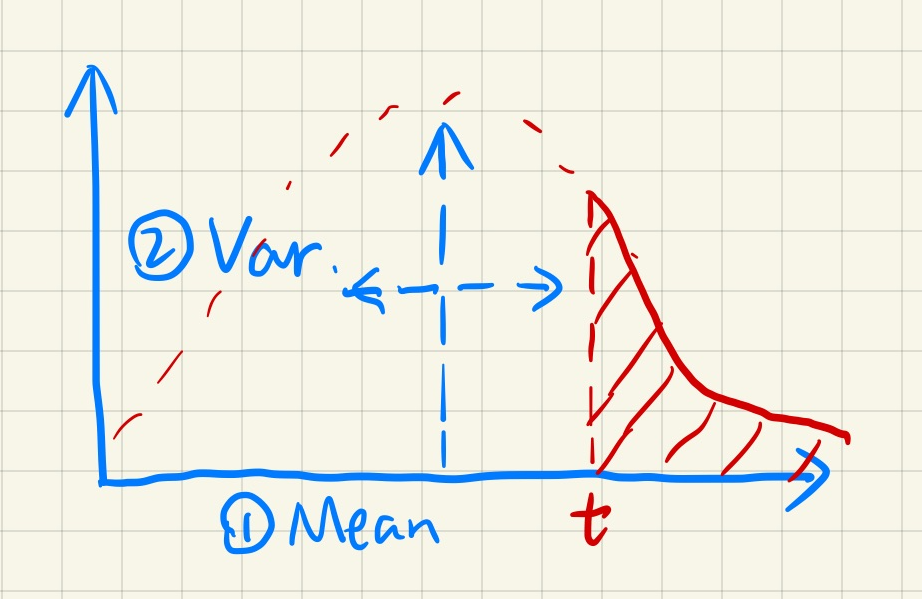
- 我们在渲染中直接作为约等号(约等式)
- 对于 \(t\ge\mu\) 效果还是不错的
- 否则估计不准确
评价
- VSSM 在查询的时候是 O(1) 的(很快),但是在生成的时候需要有些开销
- 生成 Mipmap 是硬件支持的,生成非常快
- 生成 SAT 相对较慢
- 现在解决了 PCSS 中的第三步的问题
第一步的问题(Step 1)
- blocker search
- 求出遮挡物的平均深度,而不是区域内的平均深度
- 区域内的平均深度是知道的
定义基础量
- 区域内的平均深度:\(z_{avg}\)
- blocker 的平均深度\((z<t)\):\(avg.z_{ooc}\)
- 待求的量
- non-blocker 的平均深度\((z>t)\):\(avg.z_{unooc}\)
key idea
- 满足如下的关系
\[ \dfrac{N_1}{N}z_{unooc}+\dfrac{N_2}{N}z_{ooc}=z_{avg} \]
- \(\dfrac{N_1}{N}\) 可以通过切比雪夫不等式估计
- \(\dfrac{N_2}{N}=1-\dfrac{N_1}{N}\)
- 假设 \(z_{unooc}=t\)
- 非遮挡物的深度和当前的深度相似
- 基于绝大多数阴影的接收者是一个平面
- 这种假设还是有问题的
- 接受平面是曲面
- 接受平面和光线平行
- 这种假设还是有问题的
- \(z_{avg}\) 可以通过范围查询得到
VSSM 效果
- https://developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch08.html

现状
- 人们会更多使用 PCSS 来做阴影
- 人们对于噪声的容忍度很高
- 图像空间降噪做得很好
- 尤其是结合时间维度之后
MipMap / SAT
- 快速范围查询
MipMap
- fast、approx、square
- 涉及到插值
- 层内插值(线性插值)
- 层间插值(三线性插值)
- 插值会引发不准确
- 正方形查询都会不准,对于矩形无法解决
- 各向异性过滤可以查询矩形
- 在软阴影范围比较小的情况下还是表现不错的
SAT
- summed area table
- 范围内元素平均和范围内元素综合是等价的(知道范围大小)
一维数组
- 前缀和
- 任意范围内的和可以通过两个前缀和相减得到
- 前缀和可以通过动态规划方法很快得到 \(O(n)\)
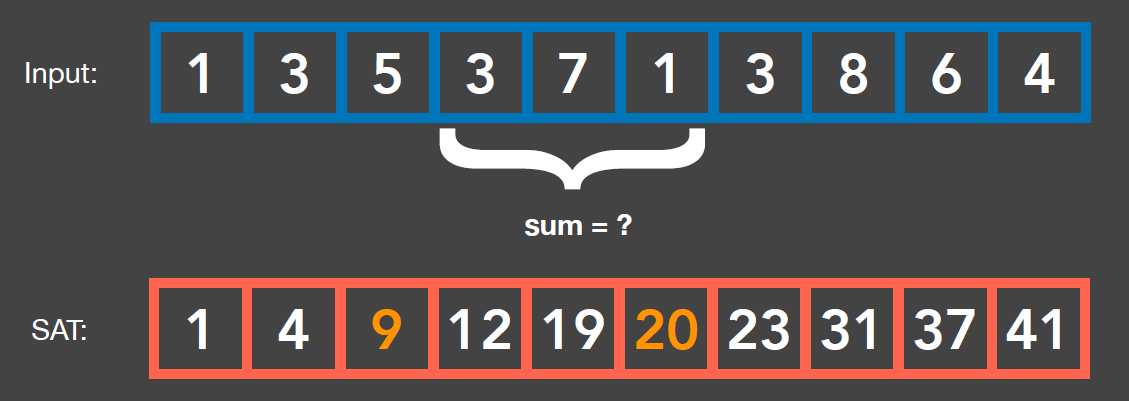
二维数组
- 忽略下图中的坐标系箭头,应该是左上角为原点才能和范围匹配

- 动态规划,\(dp[i][j]\) 记录范围 \((0,0),(i,j)\) 矩形内的面积
\[ S \left((a,b),(c,d)\right)=dp[c][d]-dp[c][b]-dp[a][d]+dp[a][b] \]
- 建表
- 每行做一遍,每列做一遍
- 复杂度 \(O(mn)\)
- 并行 \(O(m+n)\)
- 数值精度溢出问题:有可能(double 损失精度)
MSM
- Moment Shadow Mapping
VSSM 的问题
单峰假设不准
- 正态分布的假设可能不成立
- 带来的问题:计算出来的百分比不准确

- 问题
- 偏黑:问题不大,结果可以忍受
- 偏亮:问题很大(LIGHT LEAKING)
- 下图表示偏亮
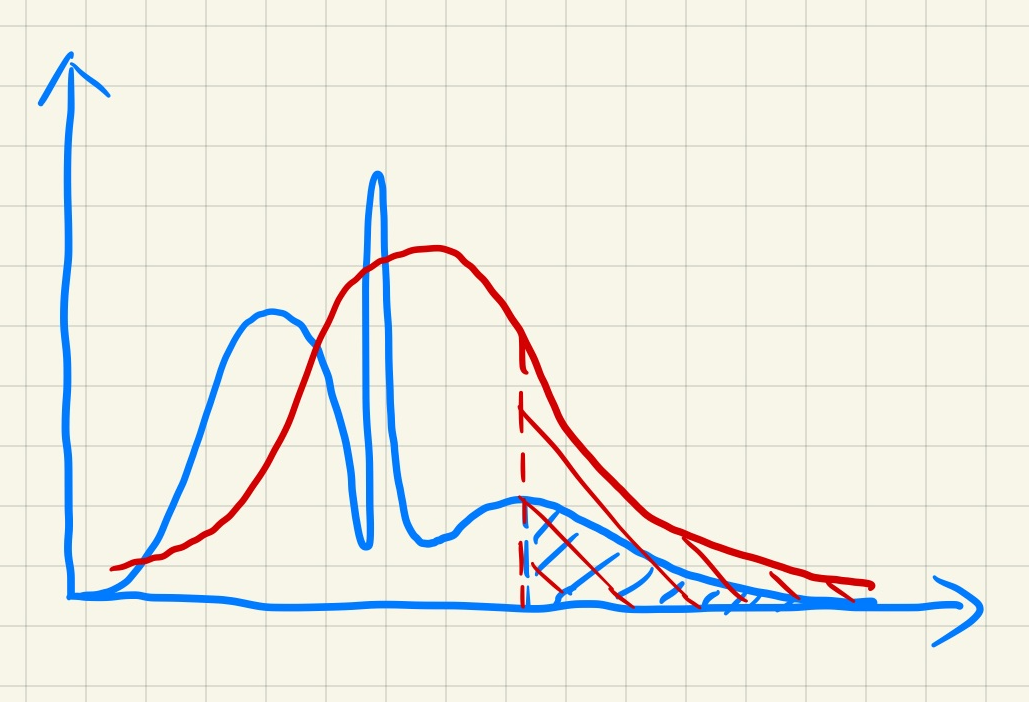
- 下图表示偏亮带来的问题
- 镂空车车底问题
- https://developer.nvidia.com/gpugems/GPUGems3/gpugems3_ch08.html

接受面不是平面
- 接收面不是平面导致假设出问题
切比雪夫不等式问题
- \(t\ge\mu\)
MSM 解决的问题
- 更精准的模拟分布
- 高阶矩(moment)描述分布
- VSSM 只使用了 \(X,X^2\)
- 保留更多阶的矩,描述的分布更准确
- 只给结论,过程复杂
- 简单来说就是某种展开,保留更多的项,结果更加准确
- first \(m\) orders of moments can represent a function with \(\dfrac{m}{2}\) steps
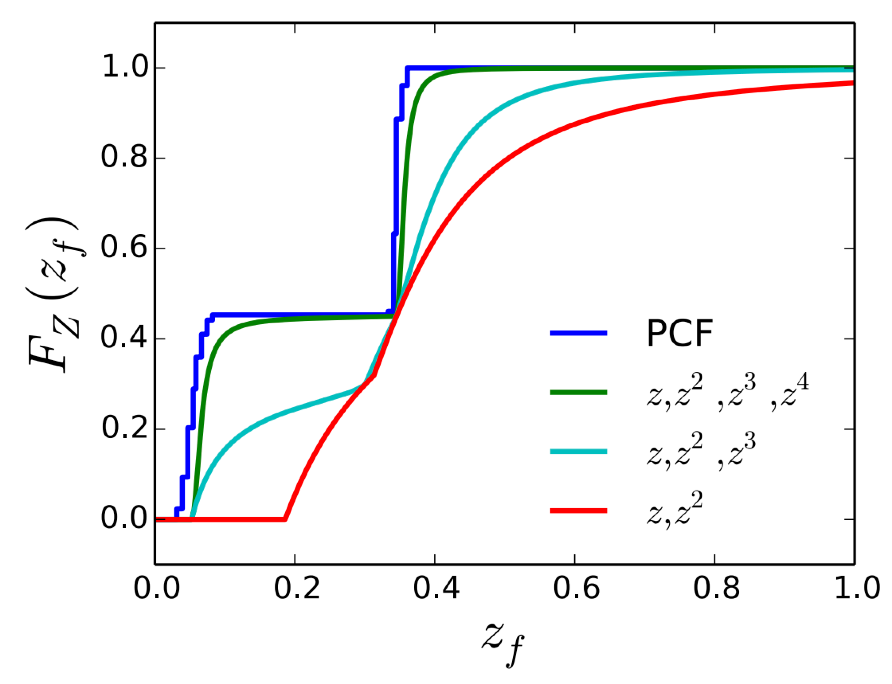
- 通常而言,4 阶矩效果就很好了
- 越多,存储开销越大
- 存储上工业界常用的方法:packing/unpacking
- 多个通道表示一个数
- 一个数表示多个通道
- 这样做的结果是不能直接插值的
- 怎么通过这些高阶矩计算出需要的值
- 论文:[Peters et al., Moment Shadow Mapping]
效果
- 解决了 light leaking 问题

DFSS
- Distance field soft shadows
- 生成软阴影
(Signed) Distance Function
- (有向)距离场
- At any point, giving the minimum distance (could be signed distance) to the closest location on an object
- 对于任意一个点,定义到到物体表面的最近距离
- 可以带符号
- 负号表示在物体内部
- SDF:Signed Distance Function
- GAMES101 中的例子:blend 一个边界
- 第一行是线性插值
- 第二行是使用 SDF 进行插值
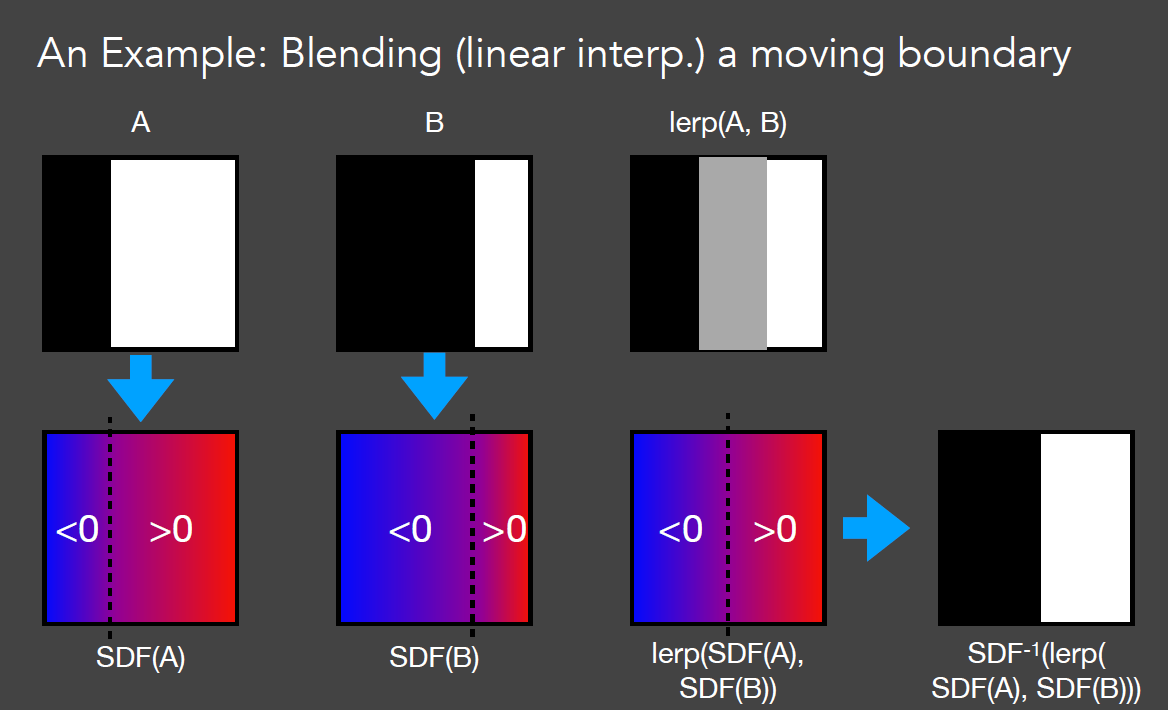
- SDF 能在几何上产生非常好的过渡
- SDF 理论基础
- 最优传输理论(optimal transport)
- 顾险峰
距离场的使用
ray marching
- https://docs.unrealengine.com/en-US/BuildingWorlds/LightingAndShadows/MeshDistanceFields/index.html
- 用于光线和物体求交

- SDF 提供了一个安全距离
- 对于一个点 x,SDF(x) 表示在一个半径为 SDF(x) 的距离之内没有物体
- 也就是说光线前进 SDF(x) 这么长的路程,一定不会打到物体上
- 也就是说,光线每次前进 SDF 中记录的距离,优化求交过程
- SDF 的计算比较麻烦,存储开销很大
- 运动物体(刚体)是可以使用 SDF 的
- 如果对每个模型计算了 SDF,求解整个场景的 SDF 只需要求每个模型 SDF 的最小值即可
- 刚体运动的 SDF 比较好计算
- 形变物体的 SDF 需要重新计算
- 比较麻烦
生成软阴影
- 任意一点的 SDF 告诉了我们一个安全距离,等价于安全角度

- 安全角度越小,意味着能够看到的东西越少
- less visibility
- 在 ray marching 的过程中,每一步都计算安全角度
- 最终的安全角度就是过程中最小的安全角度
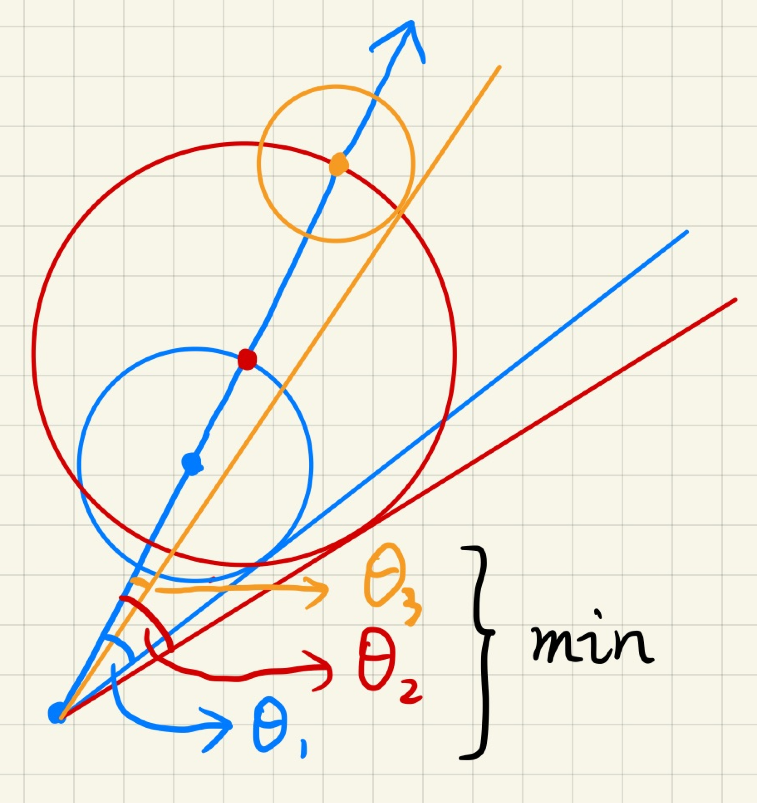
- 怎么计算安全距离
\[ \arcsin\left\{\dfrac{SDF(p)}{||p-o||}\right\} \]
- 更快的计算
- 一个近似,直接使用 \(\sin\) 的结果也可以估计出阴影的大小
- \(k\) 的作用:控制 0,1
之间的过渡带范围,也就是阴影的软硬程度
- larger k \(\leftrightarrow\) earlier cutoff of penumbra \(\leftrightarrow\) harder shadow
\[ \min\left\{\dfrac{k\cdot SDF(p)}{||p-o||},1.0\right\} \]
- 安全角度的大小决定阴影的软硬程度
- 效果

- 一个教程:https://zhuanlan.zhihu.com/p/94265891
距离场的可视化
- 很像是物体的描边
- https://docs.unrealengine.com/en-US/BuildingWorlds/LightingAndShadows/MeshDistanceFields/index.html

距离场做软阴影的评价
- 好处
- 快:在 ray marching 的同时计算出软阴影
- 生成 SDF 的过程相对耗时
- 高质量
- 快:在 ray marching 的同时计算出软阴影
- 问题
- 需要预先计算 SDF
- 需要较大的存储(3D)
- 优化存储:八叉树、kd 树等
- artifacts
其他
- https://github.com/protectwise/troika/tree/master/packages/troika-three-text
- 利用距离场实现无限分辨率的字母
- SDF 生成的物体表面非常不好贴纹理,参数化表面很复杂