数据库概论.陈立军.03.关系模型(2)
关系模型
关系代数的分类
- 基本运算
- 一元运算
- 选择、投影、更名
- 多元运算
- 笛卡儿积、集合并、集合差
- 一元运算
- 扩展运算
- 集合交、\(\theta\) 连接、自然连接、外连接
- 其它运算
- 赋值、广义投影、插入、删除、更新
关系代数基本运算
选择运算
- 在关系中选择满足给定条件的元组(行角度)
\[ \sigma_F(R)=\left\{t|t\in R,F(t)=true\right\} \]
- \(F\) 是选择的条件,\(\forall t\in R,F(t)\) 要么为真,要么为假
- \(F\) 由逻辑运算符连接算术表达式而成
- 逻辑运算符:\(\land, \lor,\lnot\)
- 算术表达式:\(X\ \theta\ Y\)
- \(X,Y\)是属性名、常量、或简单函数
- \(\theta\) 是比较算符
- \(\theta\in\left\{>,\ge,<,\le,=,\ne\right\}\)
- 例子:找年龄不小于 20 的男学生
- 表达上等效
- 实际查询中谁更高效?取决于数据库的设计
- 如果索引中含有 age,则 (3) 可能最高效
- 一般不会是(2),性别这种二值属性不适于建索引
\[ \begin{aligned} (1)\ &\sigma_{age\ge20\land sex='M'}(S)\\ (2)\ &\sigma_{age\ge20}\left(\sigma_{sex='M'}(S)\right)\\ (3)\ &\sigma_{sex='M'}\left(\sigma_{age\ge20}(S)\right)\\ \end{aligned} \]
投影运算
- 从关系中取若干列组成新的关系(从列的角度)
\[ %% Π𝑨𝑨𝑹𝑹=𝒕𝒕𝑨𝑨𝒕𝒕∈𝑹𝑹},𝑨𝑨⊆𝑹𝑹 \prod_A(R)\left\{ t[A]|t\in R\right\},A\subseteq R \]
- 注意:投影的结果中要去掉相同的行
- 例子:给出所有学生的姓名和年龄
- \(\prod_{sno,age}(S)\)
更名
- 将关系 \(R\) 更名为 \(S\)
- \(\rho_S(R)\)
- 对现有的表进行更名
- 将计算表达式 \(E\) 更名为关系 \(S\)
- \(\rho_{S(A_1,A_2,\cdots,A_n)}(E)\)
- 将中间结果存储到自己定义的表里面
- 更名运算的必要性
- 将更名运算施加到关系上,得到具有不同名字的同一关系
- 当同一关系多次参与同一运算时需要更名
并运算
- 所有至少出现在两个关系中之一的元组集合
\[ R\cup S=\left\{r|r\in R\lor r\in S\right\} \]
- 关系 \(R\) 和 \(S\)
进行并运算的前提是它们必须是相容的
- 关系 \(R\) 和 \(S\) 必须是同元的,其属性数目必须相同
- 对 \(\forall i\),\(R\) 的第 \(i\) 个属性和 \(S\) 的第 \(i\) 个属性的域必须相同
- 简单地说,得具有相同的表结构
- 例子:求选修了 001 号或 002 号课程的学生号
- 两种表示
- \(\prod_{sno}(\sigma_{cno=001\lor cno=002}(SC))\)
- \(\prod_{sno}(\sigma_{cno=001}(SC))\cup\prod_{sno}(\sigma_{cno=001}(SC))\)
差运算
- 所有出现在一个关系而不在另一关系中的元组集合
\[ R-S=\left\{r|r\in R\land r\notin S\right\} \]
- \(R,S\) 必须是相容的
- 例子:求选修了001号但未选修002号课程的学生号
- \(\prod_{sno}(\sigma_{cno=001}(SC))-\prod_{sno}(\sigma_{cno=002}(SC))\)
- \(\prod_{sno}(\sigma_{cno=001\land
cno\ne002}(SC))\)
- 这种表示是错误的,一方面第二个条件是多余的,另一方面不适用于如下场景
- 每个人有多个行,表示选择了不同的课程
交运算
- 所有同时出现在两个关系中的元组集合
- 交运算可以通过差运算来重写
\[ R\cap S=R-(R-S) \]
- 是一种扩展运算,早期定义的时候把差运算定义成了基本运算
- 例子:求同时选修了 001 号和 002 号课程的学生号
- \(\prod_{sno}(\sigma_{cno=001}(SC))\cap\prod_{sno}(\sigma_{cno=001}(SC))\)
- \(\prod_{sno}(\sigma_{cno=001\land
cno=002}(SC))\)
- 这种表示是错误的,结果为空
笛卡尔积运算
- 元组的连串(Concatenation)
- \(r=(r_1,\cdots,r_n), s=(s_1,\cdots,s_m)\)
- 则 \(r\) 与 \(s\) 的连串定义为
\[ \hat{rs}=(r_1,\cdots,r_n,s_1,\cdots,s_m) \]
- 关系的笛卡尔积
\[ R\times S=\left\{\hat{rs}|r\in R\land s\in S\right\} \]
- \(R\times S\) 的度为 \(R\) 与 \(S\) 的度之和
- \(R\times S\) 的元组个数为 \(R\) 与 \(S\) 的元组个数的乘积
- 计算的一个例子
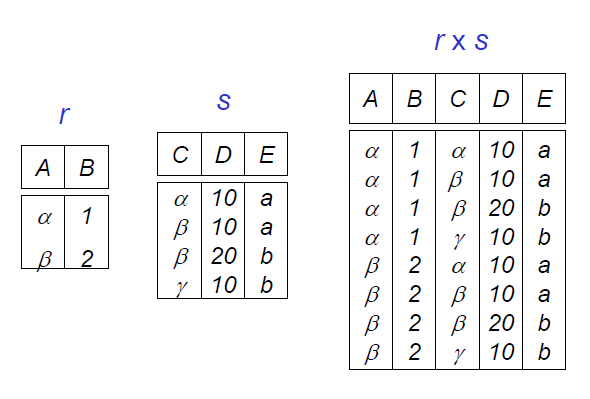
- 包打天下:选择、投影、笛卡尔积
例子 1
- 求选修 c1 课程的学生姓名
- 两个表的连接
- SN:student name
\[ \prod_{SN}\left(\sigma_{S.sno=SC.sno\land R.cno=c1}(S\times SC)\right) \]
例子 2
- 表 S
| 姓名 | 课程 | 成绩 |
|---|---|---|
| A | a | 80 |
| B | b | 70 |
| C | b | 90 |
- 另外一个例子:课程 b 成绩比 A 高的成员
- 自己和自己连接,更名
\[ \prod_{S.姓名}\left(\sigma_{R.姓名=A \land R.课程=b\land S.课程=b\land S.成绩>R.成绩}(S\times\rho_R(S))\right) \]
- 如果要比较同一个表里的三行,则可能需要再乘一次
关系代数扩展运算
\(\theta\) 连接
- 因为这个操作很常见,抽象成一个运算
- 从两个关系的广义笛卡尔积中选取给定属性间满足一定条件的元组
\[ R{\bowtie\atop A\ \theta\ B}S=\left\{\hat{rs}|r\in R\land s\in S\land r[A]\ \theta s[B]\ \right\} \]
- \(\theta\) 为算术比较符,为等号时称为等值连接
- A, B 为 R 和 S 上度数相等且可比的属性列
- 例子:笛卡尔积运算的例子 2
\[ \prod_{S.姓名}\left(\left(\sigma_{R.姓名=A \land R.课程=b}\right){\bowtie\atop R.成绩<S.成绩}\left(\sigma_{S.课程=b}\right)\right) \]
自然连接
- 从两个关系的广义笛卡儿积中选取在相同属性列 B 上取值相等的元组,并去掉重复的列
\[ R\bowtie S=\left\{\hat{rs}[\bar{B}]|r\in R\land s\in S\land r[B]=s[B]\right\} \]
- 自然连接与等值连接的不同
- 自然连接中相等的分量必须是相同的属性组,并且要在结果中去掉重复的属性,而等值连接则不必
- 自然连接要求必须有公共的列,等值连接只要求可比
- 自然连接非常有用
- 实体之间的联系在自然连接之后能够合成一张表
- 例子
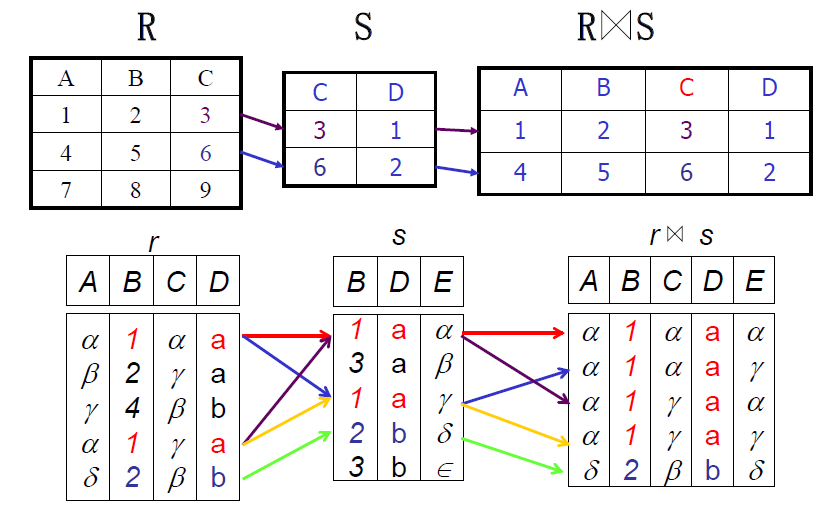
- 相同属性列的相同元素越多,结果行数越多
- 如果全部相同,退化为笛卡尔积
- 例子:求001号学生所在系的名称
- \(\prod_{dname}(\sigma_{sno=001}(S\bowtie dept))\)
- \(\prod_{dname}((\sigma_{sno=001}(S))\bowtie
dept)\)
- 效率更高
- 一般而言,我们先做选择,再做连接
- 先做连接可能出来很大的表
例子
- 关系 \(R(A, B)\)、\(S(A, C)\)、\(R\) 与 \(S\) 中元组个数分别为10,15
- 不考虑空值的情况
| 条件 | 表达式 | 最小元组数 | 最大元组数 |
|---|---|---|---|
| 无任何条件 | \(R\bowtie S\) | 0 (R 的 A 属性和 S 的 A 属性都不相等) |
150 (都相等) |
| 无任何条件 | \(\prod_{A}(R)\bigcup \prod_{A}(S)\) | 1 (都相等) |
25 (都不相等) |
| A 是 R 的主码 | \(R\bowtie S\) | 0 (R 的 A 属性和 S 的 A 属性都不相等) |
15 (S 里的一行最多只能够和 R 的一行连接) |
| A 是 R 的主码 | \(\prod_{A}(R)\bigcup \prod_{A}(S)\) | 10 | 25 |
| A 是 R 的主码 且 A 是 S 的外码 |
\(R\bowtie S\) | 15 (外码) |
15 (S 里的一行最多只能够和 R 的一行连接) |
| A 是 R 的主码 且 A 是 S 的外码 |
\(\prod_{A}(R)\bigcup \prod_{A}(S)\) | 10 (外码 + 主码) |
10 (外码 + 主码) |
- A 是 R 的主码表示 A 中的 R 各不相同
- A 是 S 的外码,则 S 在 A 上的取值必须在 R 的 A 上出现(参照完整性)
自然连接的问题
- 如果某个元素在某个表中缺失的话,结果将会有些元素缺失
- 解决方案:外连接
外连接
为避免自然连接时因失配而发生的信息丢失,可以假定往参与连接的一方表中附加一个取值全为空值的行,它和参与连接的另一方表中的任何一个未匹配上的元组都能匹配,称之为外连接
外连接 = 自然连接 + 未匹配元组(悬挂元组)
外连接的形式:左外连接、右外连接、全外连接
- 左外连接 = 自然连接 + 左侧表中未匹配元组
- ⟕
- 右外连接 = 自然连接 + 右侧表中未匹配元组
- ⟖
- 全外连接 = 自然连接 + 两侧表中未匹配元组
- ⟗
- 左外连接 = 自然连接 + 左侧表中未匹配元组
外连接不满足结合律
例子 1
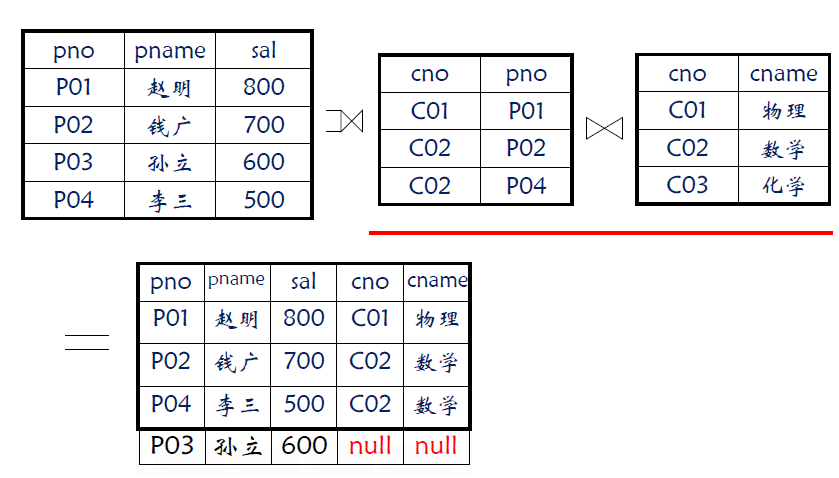
例子 2
- 外连接不满足结合律
- 这个例子的巧妙之处在于:AB、BC、CA
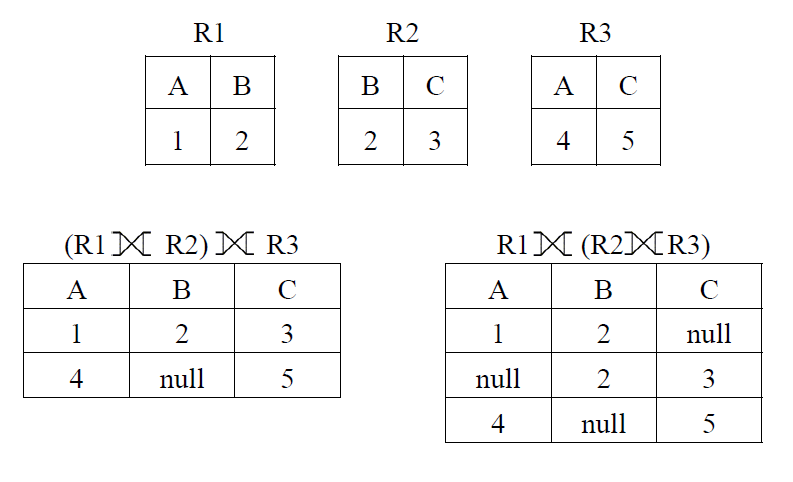
半连接
- \(R⋉S\)
- 提取出 R 里面能和 S 参与自然连接的那些行
- 反半连接
- 提取出 R 里面不能和 S 参与自然连接的那些行
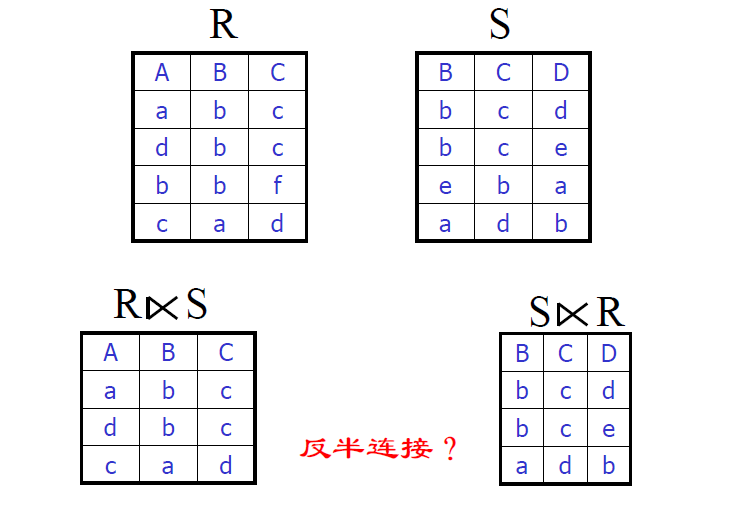
- 反半连接的应用场景
- 物理底层的 not in/not exist 查询
- 半连接的应用场景:减少分布式数据库的数据传输
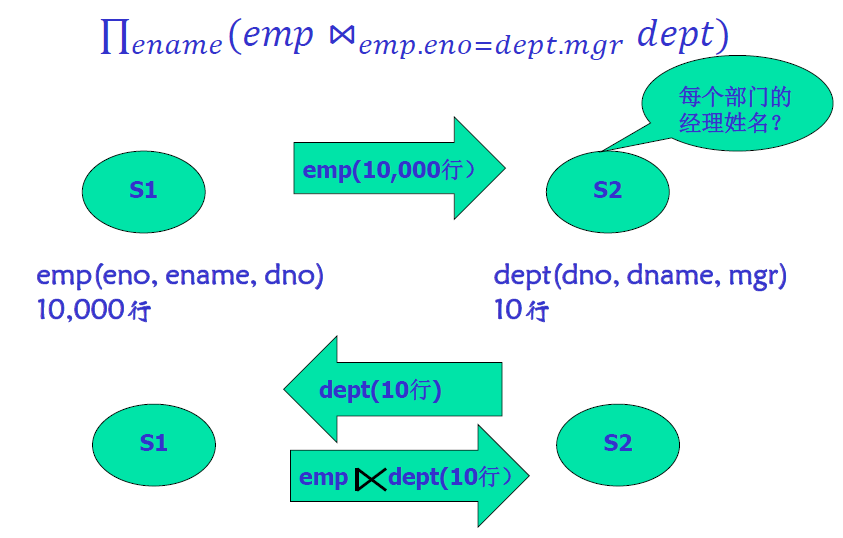
外部并
- outer union
- R(AB) outer join S(BC)
- 在 B 上相同的行为合并成一行
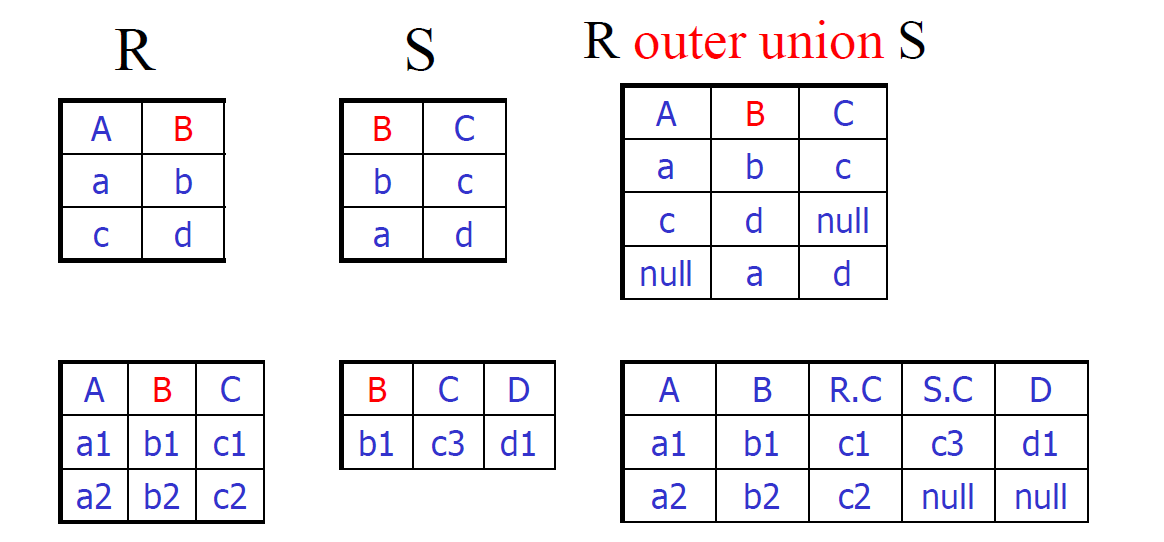
- 子实体集合合并为父实体集合
- 例子:不同部门收集客户信息,然后将不同部门收集的信息整合起来
- \({\color{red}\mathrm{TODO}}\)
- 外部并和全外连接的区别?没啥区别
象集
- 除法
- 应用场景:找到选修了所有课程的同学
- 涉及到所有、全部问题
- 关系 \(R(X,Z)\),\(X,Z\) 是属性组,\(x\) 是 \(X\) 上的取值,定义 \(x\) 在 \(R\) 中的象集为
\[ Z_x=\left\{t[Z]|t\in R\land t[X]=x\right\} \]
- 象集:先选择,后投影
- 从R 中选出在 X 上取值为 x 的元组,只留 Z 属性
- \(Z_x\)
例子
- 如何求得选修了全部课程的学生?
思路 1
- 判断每个学生的课程象集是否包含了整个课程集合 C
\[ \left\{u|r\in SC\land u=r[姓名]\land 课程名_{u}\supseteq C\right\} \]
思路 2
- 判断学生与课程集合构成的笛卡尔积是否完全包含在选课集合中
\[ \left\{u|u\in\prod_{姓名}(SC)\land\forall v\in C(\hat{uv}\in SC)\right\} \]
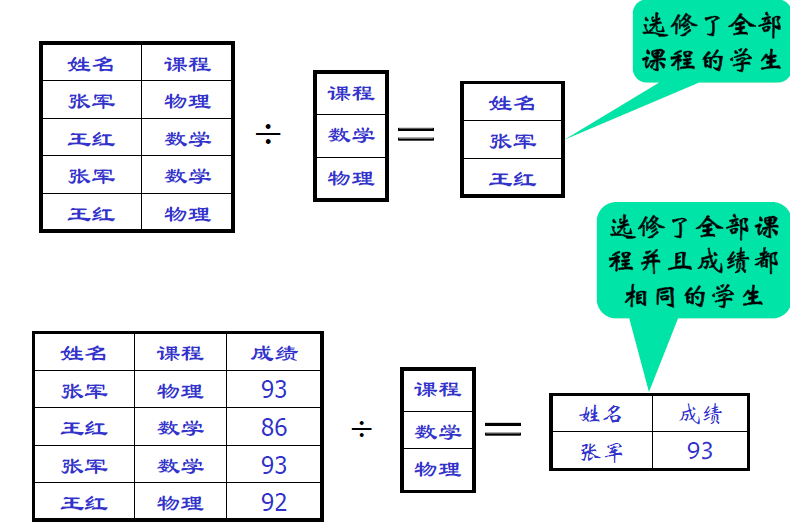
- 理解图示
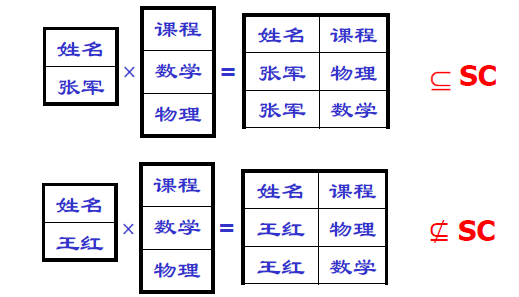
除法
- 所有、全部、任意问题
- 定义表达式(2 种)
- 上面提到的两种方式
\[ R(X,Y)\div S(Y)=\left\{x|r\in R\land x=r[X]\land Y_x\supseteq S\right\} \]
\[ R(X,Y)\div S(Y)=\left\{u|u\in\prod_X(R)\land\forall v\in S(\hat{uv}\in R)\right\} \]
- 计算表达式
- 巧妙了
- 先计算出不存在的关系,如果有不存在的说明就不是完全
\[ R(X,Y)\div S(Y)=\prod_X(R)-\prod_X\left(\prod_X(R)\times\prod_{Y}(S)-R\right) \]
- 减法计算
- 补集:区分两类不同性质的子集
- 表结构必须相同
例子
- SC(sno, cno, grade)
- 求选修了所有课程的学生
- 方案1:\(\prod_{sno,cno}(SC)\div \prod_{cno}(C)\)
- 方案2:\(\prod_{sno}(SC\div \prod_{cno}(C))\)
- 方案 2 是错误的
- 除法的 X 表示 “课程+成绩”
关系代数查询实例
求没有选修 c1 号课程的学生
- 没有:求补
- 所有学生 – 选修了c1号课程学生
\[ \prod_{sno}(SC)-\prod_{sno}(\sigma_{cno=c1}(SC)) \]
- \(\prod_{sno}(\sigma_{cno\ne
c1}(SC))\)
- 这是错误的
- 可能有人选了好几门课,注意这是对每条记录进行处理判断的
- 这个表示的含义:仅选 c1 号课程之外的其他学生(类 2 + 类 3)
- 选了其他不是 c1 的课的学生
- 所有的人分为 3 类
- 类1:只选了 c1(只选了一门课,就是 c1)
- 类2:没有选 c1 (选了课,但是没有选 c1)
- 类3:选了好几门课,其中有一门是 c1(至少选了两门课)
求仅选修了 c1 号课程的学生号
- 所有的学生-仅选 c1 号课程之外的学生
- 所有的学生 - (类 2 + 类 3)
\[ \prod_{sno}(SC)-\prod_{sno}(\sigma_{cno\ne c1}(SC)) \]
- 选修 c1 号课程的学生-仅选 c1 号课程之外的学生
- 对上面的 3 类人进行判断
\[ \prod_{sno}(\sigma_{cno=c1}(SC))-\prod_{sno}(SC-\sigma_{cno=c1}(SC)) \]
- 上面两个式子减去的部分等价
求选修 c1 课程比 s1 学生的该门课程成绩高的学生
sno, cno, G
笛卡尔积
\[ \prod_{S.sno}\left(\sigma_{R.sno=s1\land R.cno=c1\land S.cno=c1\land R.G< S.G}\left(\rho_R(SC)\times\rho_S(SC)\right)\right) \]
求每门课程的先修课的先修课
- cno, pcno
- 递归查询
\[ \prod_{C.cno,R.pcno}\left(\sigma_{C.pcno=R.cno}\left(C\times\rho_R(C)\right)\right) \]
- 怎么查找所有的祖辈先修课?
- 传递闭包
- 从关系完备性来讲,我们目前的关系运算符是不够完备的,不能够表示这种运算
- 现在的主流数据库是支持递归查询的
求选修了至少两门课的学生
- sno, cno, G
\[ \prod_{R.sno}\left(\sigma_{R.sno=S.sno\land R.cno\ne S.cno\left(\rho_R(SC)\times\rho_S(SC)\right)}\right) \]
- 求选修了至少 N 门课的学生
- \({n \choose2}\) 个不等号
- 求只选修了 1 门课的学生
- 所有同学 - 至少选修了两门课的同学
求最低的成绩
- sno, cno, G
- 笛卡尔积
\[ \prod_G(SC)-\prod_{S.G}\left(\sigma_{R.G<S.G}\left(\rho_R(SC)\times\rho_S(SC)\right)\right) \]
- 小于等于好像不行,多个值的时候会变成空集
求选修课程中包含了所有 S01 号学生所选修课程的学生号
- cno, sno
- 除法
\[ \prod_{cno,sno}(SC)\div\prod_{cno}(\sigma_{sno=S01}(SC)) \]
找出一直上涨的股票
- stock(sno, date, price)
- 上涨过的股票
\[ \prod_{R,sno}\left(\sigma_{R.sno=S.sno\land R.date>S.date\land R.price>S.price}\left(\rho_R(stock)\times\rho_S(stock)\right)\right) \]
- 一直上涨的股票
- 持续上涨的股票 = 所有股票 -下跌过的股票
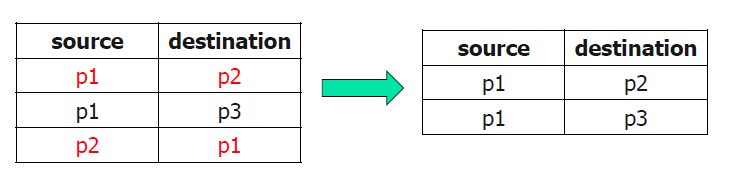
去重
- guanxi(source,destination)
- 可交换的
- 序列号可比
 \[
guanxi-\prod_{S.S,S.D}\left(\sigma_{R.D=S.S\land R.S=S.D\land
R.S<S.S}\left(\rho_R(guanxi)\times\rho_S(guanxi)\right)\right)
\]
\[
guanxi-\prod_{S.S,S.D}\left(\sigma_{R.D=S.S\land R.S=S.D\land
R.S<S.S}\left(\rho_R(guanxi)\times\rho_S(guanxi)\right)\right)
\]
关系代数更新运算
赋值运算
- 为使查询表达简单、清晰,可以将一个复杂关系代数表达式分成几个部分
- 每一部分都赋予一个临时关系变量
- 该变量可被看作关系而在后续表达式中使用
- 临时关系变量 \(\leftarrow\) 关系代数表达式
- 尽可能在一个表达式内写完
广义投影
- 在投影列表中使用算术表达式来对投影进行扩展
\[ \prod_{F_1,F_2,\cdots,F_n}(E),\ F_i是算术表达式 \]
数据库修改:删除
- 将满足条件的元组从关系中删除
- \(R\leftarrow R-E\)
- 是对永久关系的赋值运算
例子
- 删除 001 号老师所担任的课程
\[ PC\leftarrow PC-\sigma_{pno=001}(PC) \]
- 删除没有选课的学生
- 注意减法的表结构必须相同
\[ S\leftarrow S-\left(\prod_{sno}(S)-\prod_{sno}(SC)\right)\bowtie S \]
数据库修改:插入
- 插入一个指定的元组,或者插入一个查询结果
\[ R\leftarrow R\ \bigcup E \]
例子
- 加入计算机系学生选修 “数据结构” 的信息
- SC: sno,cno,G(学号、课程、成绩)
\[ SC\leftarrow SC\bigcup\left(\prod_{sno}\left(S\bowtie\sigma_{dname="计算机系"}(DEPT)\right)\times \prod_{cno}\left(\sigma_{name="数据结构"}(C)\right)\times{\color{red}\{null\}}\right) \]
- 缺少成绩信息,一个 trick,和一个
null属性相乘(笛卡尔积)
数据库修改:更新
- 利用广义投影改变元组的某些属性上的值
\[ \prod_{F_1,F_2,\cdots,F_n}(E) \]
例子
- 给每位老师上调 10% 的工资
\[ PROF\leftarrow \prod_{pno,pname,sal\leftarrow sal*1.1,dno}\left(PROF\right) \]
- 对工资超过 3000 的老师征收 5% 所得税
\[ PROF\leftarrow \left(\prod_{pno,pname,sal\leftarrow sal*1.1,dno}\left(\sigma_{sal>3000}PROF\right)\right){\color{red}\bigcup\left(\sigma_{sal\le 3000}(PROF)\right)} \]