GAMES202.闫令琪.03.实时阴影(1)
- https://www.bilibili.com/video/BV1YK4y1T7yY
Real-Time Shadows
- 实时阴影
Shadow Mapping
- SM
- 经典的两趟算法
- 2-pass
算法步骤
- 第一遍渲染,转换到以光源为视点的观察坐标系,记录下深度图
- 第二遍正常渲染,对每个点,转换到以光源为视点的观察坐标系中判断可见性
- 判断可见性的时候深度一致即可,可以使用原来的线性距离或者投影之后的 z 值
评价
- 图像空间的算法
优点
- 绘制阴影的时候,不需要知道场景的几何信息
缺点
- artifacts
- self occlusion 自遮挡
- aliasing 走样
自遮挡问题
- self occlusion

- 地板上的平面出现了自遮挡现象
- 由于数值精度造成的(分辨率)
- shadow map 精度有限,投射出去就是图中的红色小片
- 例如蓝色的视线应该是能看到红色的部分的,但是由于精度问题,shadow map 中记录的是橙色的值,导致我们判断红色部分不可见,从而产生自遮挡现象
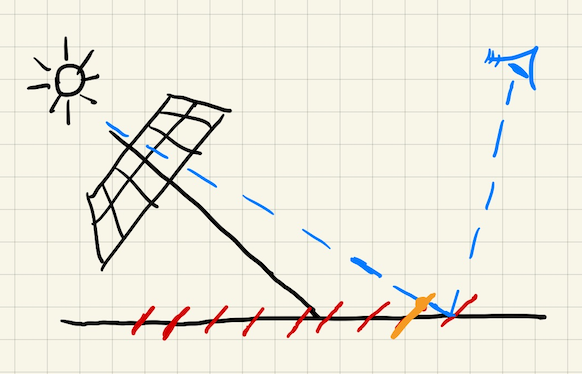
- 如果光线和物体表面垂直,此时没有这个问题
- 光线和法线重合
- 如果光线和物体表面成一个很小的角度时,自遮挡问题很严重
- 光线和法线夹角很大
- grazing angle
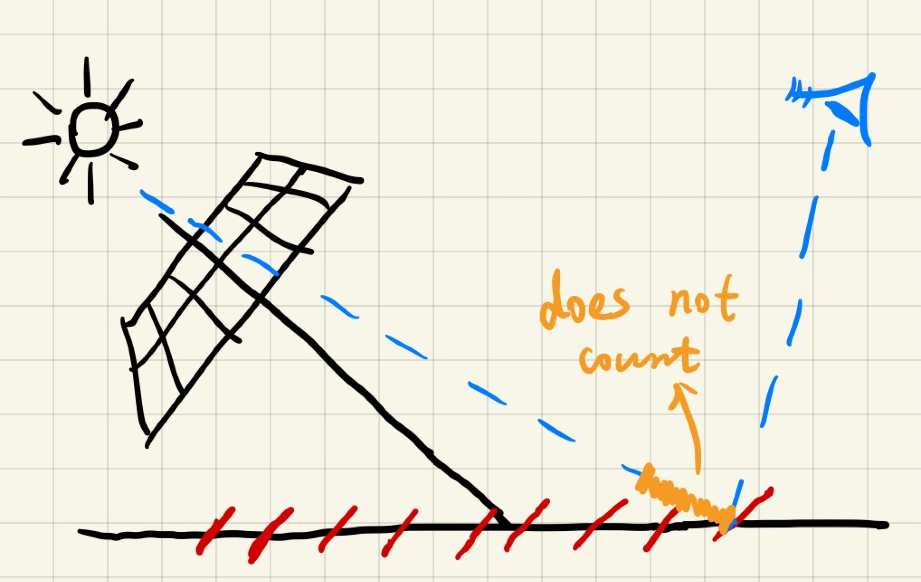
解决方案
- 增加一个 bias
- 中间的黄色那段我们不算
- 也就是说我们对计算得到的深度减去一个 bias
- 一些技巧:动态的 bias
- 当光线和物体表面法线夹角比较大时,bias 也需要比较大
- 当光线和物体表面法线夹角比较小时,bias 比较小即可
引入 bias 带来的问题
- detached shadow
- 不接触的阴影
- 鞋子部分的阴影消失了

- 工业界 100% 解决这个问题的方法现在还没有
- 解决方法还是通过找一个合适的 bias,让自遮挡和detached shadow 都不出现
- 最简单的方式
- 学术界的方法(工业界用的人少)
- second-depth shadow mapping
second-depth shadow mapping
- 不使用 bias
- 记录最小深度的同时,还记录第二小的深度
- 实际比较的时候使用这两个深度的平均值
- 能够解决之前的问题
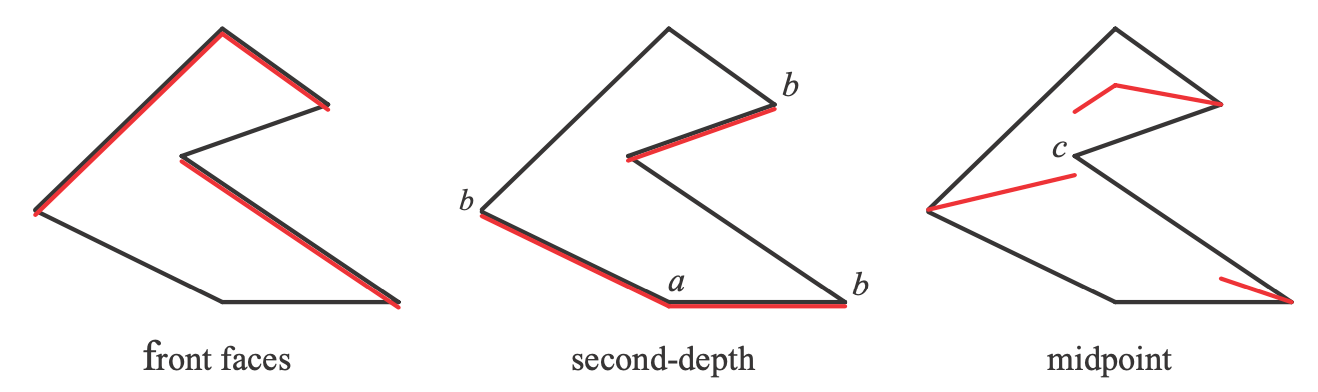
- 这个方法的问题
- 每个物体都得是一个几何实体
- 不能是一张平面,如果是一张纸的话,得描述成一个很扁的长方体
- 实现这个算法很困难,复杂度没有变化,但是无法并行
- 每个物体都得是一个几何实体
- 一些 trick
- 如果是最外层的地板,在做第一趟渲染深度图的时候不渲染地板
- 实时渲染不相信复杂度,只相信实时运行的速度
- RTR does not trust in COMPLEXITY
- 常数也很重要
走样问题
- 阴影分辨率的问题
- 高端的做法
- 给不同位置不同的分辨率
- 软影
SM 的数学原理
常用不等式
- Schwarz Inequality
- 施瓦茨不等式
\[ \left[\int_a^bf(x)g(x)dx\right]^2\le\int_a^bf^2(x)dx\cdot \int_a^bg^2(x)dx \]
- Minkowski Inequality
- 明可夫斯基不等式
\[ \left[\int_a^b\left[f(x)+g(x)\right]^2dx\right]^{\frac{1}{2}}\le\left[\int_a^bf^2(x)dx\right]^{\frac{1}{2}}\cdot \left[\int_a^bg^2(x)dx\right]^{\frac{1}{2}} \]
- 实时渲染中我们关心约等,而不是不等
- 在近似条件下约等
RTR 中的一个常用近似
\[ {\color{red}\int_\Omega f(x)g(x)dx\approx \dfrac{\int_\Omega f(x)dx}{\int_\Omega dx}\cdot {\int_\Omega g(x)dx}} \]
- 分母的部分表示归一化常数
- 例如 \(f(x)=2\)
- 什么时候近似正确呢?(满足一个条件即可)
- small support
- \(g(x)\) 的积分域很小的时候
- smooth integrand
- \(g(x)\) 在积分域内变化不大
- 图形学学术界中的 smooth:min、max 差别不大
- small support
应用于渲染方程
- 忽略自发光
\[ L_o(p,\omega_o)= \int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)V(p,\omega_i)\cos\theta_id\omega_i \]
- 利用上面的近似
\[ L_o(p,\omega_o)\approx \dfrac{\int_{\Omega^+}V(p,\omega_i)d\omega_i}{\int_{\Omega^+}d\omega_i}\cdot\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)\cos\theta_id\omega_i \]
- 这样子的近似把可见性从 shading 部分抽离出来了
- 我们做 shadow mapping 方法的原理
shadow mapping 的原理
- 什么时候是准确的?
- small support
- 积分范围只有一个点 \(\to\) 点光源、方向光源
- 做硬阴影的数学基础
- smooth integrand
- diffuse bsdf / constant radiance area lighting
- diffuse BSDF + 面光源
- 解释 shadow mapping 算法不适合的场景
- 环境光照(可以理解为超级大的面光源)+ glossy BRDF
PCSS
- Percentage Closer Soft Shadows
- 生成软阴影的一种算法
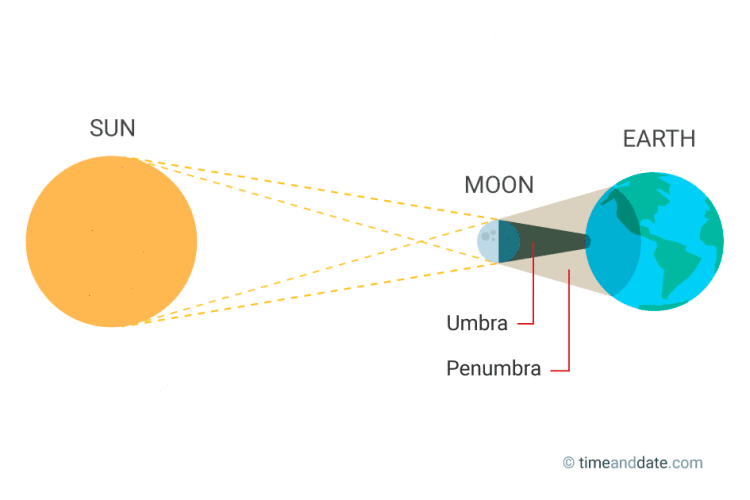
软阴影

- 生活中的现象:太阳
- 半影
PCF
- Percentage Closer Filtering
- 这个技术是用于于抗锯齿的,而不是用于生成软阴影的(PCSS 是用于生成软阴影的)
- Filtering the results of shadow comparisons
- 先采样,后做平均(filter)
- 为什么不能先对 SM 做 filter,后采样?
- Texture filtering just averages color components, i.e. you’ll get blurred shadow map first
- Averaging depth values, then comparing, you still get a binary visibility
- 这样的操作最后得到的结果还是非 0 即 1 的,没有意义
- 原来判断一个点的可见性是直接做一次判断
- shading point 和在深度图中对应位置记录的深度值作比较
- PCF 的想法是对其周围的几个点都做阴影判断,最后把得到的结果平均起来
- shading point 和在深度图中对应位置周围的几个点的深度作比较
- 最后得到的可见性是一个 0 - 1 之间的值
- 可以加权
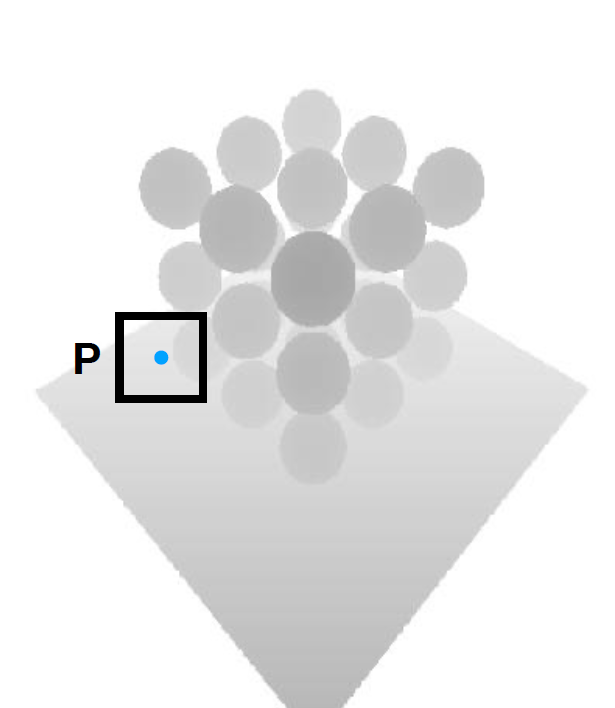
- PCF 的结果

- 时间开销:变成原来的 k 倍(k 为核的大小)
- filter size
- small:sharper
- large:softer
- 决定分辨率,核越大,量化越细
- 核的大小应该怎么确定?
- 核的大小决定了阴影的软硬程度,根据阴影的软硬需求动态调整核的大小
PCSS
- PCF 的思想,动态调整核的大小
- 什么地方需要硬阴影,什么地方需要硬阴影?
- 遮挡物和阴影的距离
- 距离越大,阴影越软
- 距离越小,阴影越硬

- 根据上面的启发,定义一个距离函数,通过这个距离函数计算核的大小
- Filter size <-> blocker distance
- More accurately, relative average projected blocker depth!
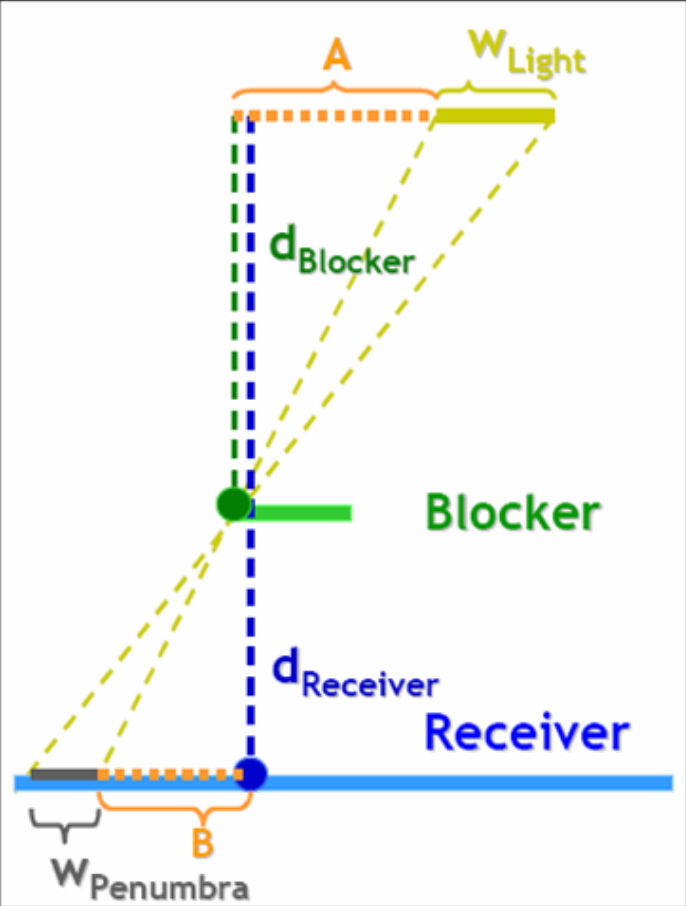
- 根据相似三角形
- penumbra:半影
\[ w_{penumbra}=\dfrac{d_{Receiver}-d_{Blocker}}{d_{Blocker}}\cdot w_{Light} \]
- 这个式子也符合我们生活中的观察
- Blocker 离 Receiver 越近,那么阴影越硬(\(w_{penumbra}\) 越小)
- \(d_{Blocker}\):average blocker
depth
- blocker 可能并不是一个点,有一定的范围,计算他们的平均值
- 看 SM 中对应位置有多少个点能挡住 shading point,求他们的平均值
- 面光源本身是没法生成一个 SM 的,我们模拟面光源的软阴影,用一个点光源代替它生成一个 SM
PCSS 流程
- Step 1: Blocker search
- getting the average blocker depth in a certain region
- 将这些点在 SM 中的深度值和我们计算出来的深度值作比较
- 感觉这个时候还是当作点光源操作
- 考虑的是平均的 blocker 的深度,如果不是 blocker 则不管这个像素
- Step 2: Penumbra estimation
- use the average blocker depth to determine filter size
- Step 3: Percentage Closer Filtering
问题
- 怎么决定第一步搜索 blocker 的范围
- 可以设置为一个常数,例如 5x5
- 可以通过启发式计算出搜索范围
- 比较慢,时间开销大
其他
- 多光源,如果利用 SM,需要对每个光源计算一个 SM