GAMES101.闫令琪.13.动画与模拟(2)(Lecture 22)

Posted on Edited on In Views:
欧拉方法、中点法、自适应步长方法、龙格库塔方法、RK4、流体的模拟、两大流派（拉格朗日方法、欧拉方法）
  • https://www.bilibili.com/video/av90798049

动画与模拟

单个粒子的模拟

  • 假设单个粒子在速度场中运动
    • 理想，实际很难找到一个速度场
  • 解常微分方程
    • ODE：Ordinary Differential Equation

\[ \dfrac{dx}{dt}=\dot{x}=v(x,t) \]

欧拉方法

  • 前向欧拉方法，显式欧拉方法
  • 简单的迭代方法
  • 广泛的使用

\[ \begin{aligned} \boldsymbol{x}^{t+\Delta t}=\boldsymbol{x}^{t}+\Delta t \dot{\boldsymbol{x}}^{t} \\ \dot{\boldsymbol{x}}^{t+\Delta t}=\dot{\boldsymbol{x}}^{t}+\Delta t \ddot{\boldsymbol{x}}^{t} \end{aligned} \]

  • 始终用上一个时刻的数据计算这一时刻的数据

存在的问题

不准确

  • 很不准确
    • 可以通过减小步长来解决

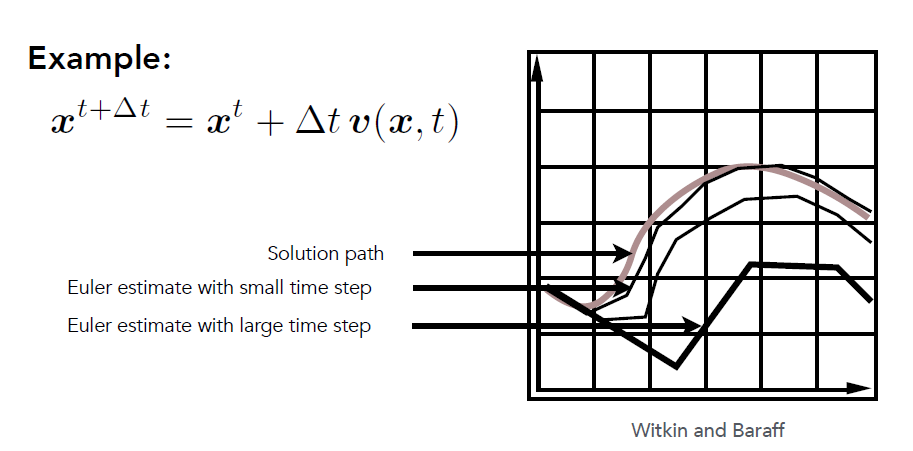
不稳定

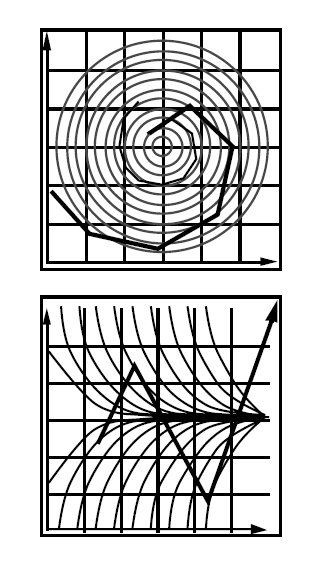
  • 通常会趋于不稳定
    • 例如下面的两个场景
      • 场景1：只要有一小段步长，就会脱离螺旋线
      • 场景2：不能汇聚到中心，反而离中心越来越远（正反馈）

问题的比较

  • Errors
    • Errors at each time step accumulate. Accuracy decreases as simulation proceeds
    • Accuracy may not be critical in graphics applications
      • CG 中，物理上不太准确没啥大关系，效果好就行
  • Instability
    • Errors can compound, causing the simulation to diverge even when the underlying system does not
      • 你有一个模拟方法，但是不管你怎么模拟都不会收敛到实际的结果
      • 发散的结果和真实的差的特别大
    • Lack of stability is a fundamental problem in simulation, and cannot be ignored
      • 不稳定是个很严重的问题

对抗不稳定性

中点法

  • Midpoint Method

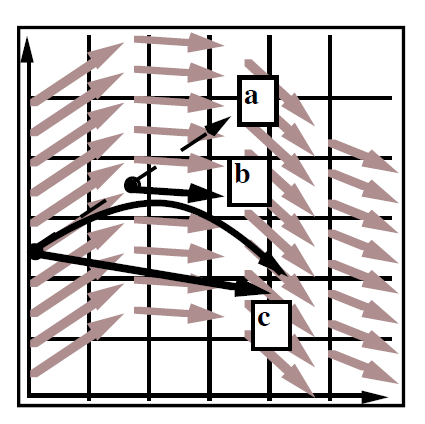
算法

  • 首先使用欧拉方法计算出下一个点的位置 a
  • 取原始点和 a 点连线的中点 b
  • 计算 b 点的方向
  • 用 b 点的方向在原始点上移动一段距离

\[ \begin{aligned} x_{mid}=x(t)+\dfrac{\Delta t}{2}\cdot v(x(t),t)\\ x(t+\Delta t)=x(t)+\Delta t\cdot v(x_{mid},t) \end{aligned} \]

评价

  • 思想：找一个更具代表性的速度
  • 中点法为什么更优？
    • 比欧拉方法多了一个二次项
  • 展开上述的公式

\[ \begin{aligned} \boldsymbol{x}^{t+\Delta t}&=\boldsymbol{x}^{t}+\Delta t\left(\boldsymbol{\dot{x}}^{t}+\dfrac{\Delta t}{2}\cdot\boldsymbol{\ddot{x}}^{t} \right)\\ &=\boldsymbol{x}^{t}+\Delta t \dot{\boldsymbol{x}}^{t}+\dfrac{(\Delta t)^{2}}{2} \ddot{\boldsymbol{x}}^{t} \end{aligned} \]

  • 是欧拉方法的一个改进

自适应步长

  • Adaptive Step Size
  • 通过估计的方式选择时间步长
  • 很实用的方法
  • 可能会导致使用很小的步长

算法

  • 定义一个阈值 threshold
  • 重复以下的步骤，直至误差小于阈值
    • Compute \(x_T\) an Euler step, size \(T\)
    • Compute \(x_{T/2}\) two Euler steps, size \(\dfrac{T}{2}\)
      • 把时间分成两段，使用两次欧拉方法
    • Compute error \(||x_{T}-x_{T/2}||\)
    • If (error > threshold) reduce step size and try again
      • 重复减半 \(\Delta T\)，直至错误小于阈值

隐式欧拉方法

  • Implicit methods
  • 后向欧拉方法
  • 使用下一帧的数据来估计这一个时刻的数据
    • 解方程组

\[ \begin{aligned} \boldsymbol{x}^{t+\Delta t}=\boldsymbol{x}^{t}+\Delta t\ \dot{\boldsymbol{x}}^{t+\Delta t} \\ \dot{\boldsymbol{x}}^{t+\Delta t}=\dot{\boldsymbol{x}}^{t}+\Delta t\ \ddot{\boldsymbol{x}}^{t+\Delta t} \end{aligned} \]

  • 如果变量描述关系没有这么简单，解方程是一个很难的问题
    • 非线性方程组
  • 一般情况下会利用优化方法来解
    • 牛顿法求根公式
  • 结果稳定性非常好
  • 怎么定义一个算法的稳定性
    • 局部每一步的误差：local truncation error (every step)
    • 总的误差：total accumulated error (overall)
  • 评价的时候看误差的阶
  • 隐式欧拉方法误差的阶是 \(1\)
    • 局部误差：\(O(h^2)\)
    • 全局误差：\(O(h)\)
    • \(h\) 表示步长，在这里是 \(\Delta t\)
  • 阶越高越好
    • 越高的话，我们可以通过减小步长的方法很快的把误差减小下来

龙格库塔方法

  • Runge-Kutta
  • 一类方法
  • 擅长求解 ODE
  • 一个用的比较多的方法：RK4（4阶）

RK4

  • 初始化
    • 初始状态、场

\[ \dfrac{dy}{dt}=f(t,y),y(t_0)=y_) \]

  • 更新方式

\[ y_{n+1}=y_n+\dfrac{1}{6}h(k_1+2k_2+2k_3+k_4) \]

\[ t_{n+1}=t_n+h \]

  • 其中

\[ \begin{aligned} k_1&=f(t_n,y_n)\\ k_2&=f(t_n+\dfrac{h}{2},y_n+h\dfrac{k_1}2)\\ k_3&=f(t_n+\dfrac{h}{2},y_n+h\dfrac{k_2}2)\\ k_4&=f(t_n+h,y_n+hk_3)\\ \end{aligned} \]

  • 可以理解为中点法的扩展，精确设计

非物理的方法

  • Position-Based / Verlet Integration
    • 只通过调整位置，使其最后满足某种性质
  • 在渲染上很好用
  • 不是基于物理的，会不满足物理现象（）能量损失极快

刚体的模拟

  • 不会形变
  • 类似粒子，但是需要考虑更多的物理量
    • 位置、角度、速度、角速度

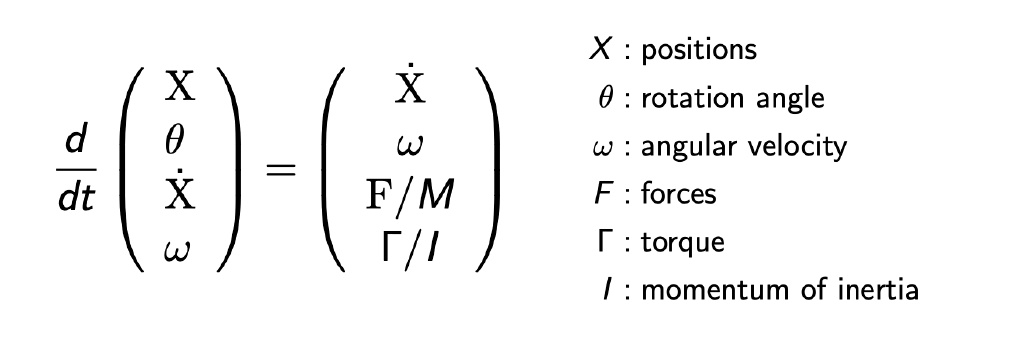
流体的模拟

  • A Simple Position-Based Method
  • 通过模拟整个形成水的体积的小球的位置来模拟整个谁的运动

key idea

  • 水体是由很多的不可压缩的刚体小球组成的
  • 水是不可压缩的（水的密度是一样的）
  • 从密度的角度出发，如果某个位置的密度发生了改变（和原来不一样），通过改变小球的运动将密度进行修正
    • 模拟水的运动
  • 需要知道密度对所有小球位置（粒子）的梯度
    • 很远的小球不影响，梯度为 0
    • 比较近的小球的会影响
  • 怎么更新（调整小球位置）
    • 梯度下降方法
    • 可能出来停不下来的现象
      • 可以人为加上运动损失

两大流派

  • Eulerian vs. Lagrangian
  • https://www.youtube.com/watch?v=iDIzLkic1pY

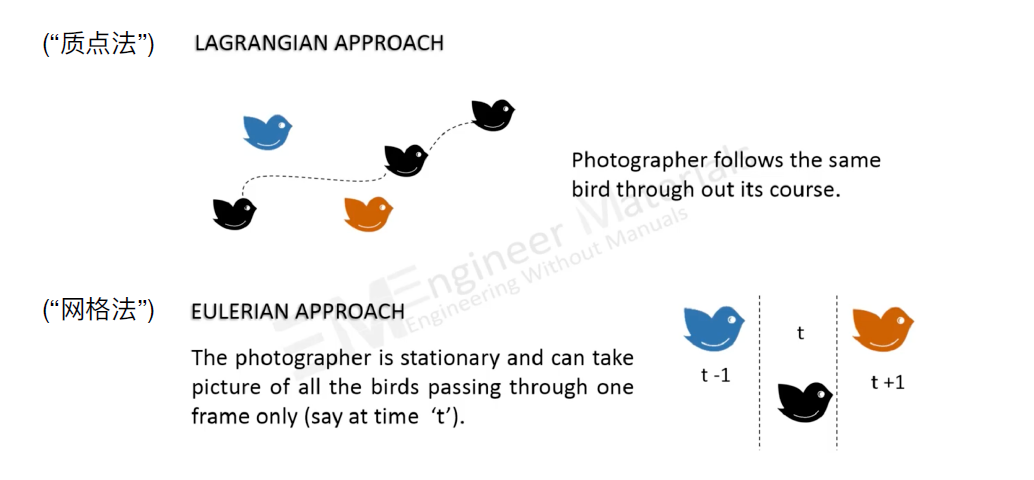
拉格朗日方法

  • 质点法
  • 跟踪每一个质点的信息

欧拉方法

  • 网格法
  • 将场景划分为若干网格
  • 跟踪每个网格的信息变化

物质点方法

  • Material Point Method (MPM)
  • 两种方法的混合

思路

  • Lagrangian: consider particles carrying material properties
    • 每一个点都带有一些属性
  • Eulerian: use a grid to do numerical integration
    • 属性的计算是以网格为单位的计算
  • Interaction: particles transfer properties to the grid, grid performs update, then interpolate back to particles
    • 网格计算完之后把这些信息写回每个点