数据库概论.陈立军.02.ER 模型(1)

Posted on Edited on In Views:
数据库设计过程（三阶段、四阶段）、ER模型基本概念（实体、联系、码、ER图）、属性类型（简单与复合、单值与多值、派生与基属性、NULL）、联系的基数（一对一、一对多、多对多）

ER 模型

  • 实体联系模型

数据库设计过程

三阶段数据库设计过程

  • 三阶段：概念结构设计、逻辑结构设计、物理结构设计
    • 出发点是基于需求分析
  • 需求分析
    • 确定存储哪些数据，建立哪些应用，常用的操作及对象有哪些等
  • 概念数据库设计
    • 对需求分析所得到数据的更高层的抽象描述
    • ER 模型、UML
  • 逻辑数据库设计
    • 将概念模型所描述的数据映射为某个特定的 DBMS 模式数据
  • 物理数据库设计

四阶段数据库设计过程

  • 把逻辑结构设计进行细分
  • 概念阶段
    • 发掘实体及其联系
    • 发掘业务规则
  • 逻辑阶段
    • 规范化设计
  • 实现阶段
    • 选择数据类型、定义表、约束、触发器
  • 物理阶段
    • 索引、磁盘组织

不同数据库设计阶段中的术语称谓

阶段 表术语 列术语 行术语
关系理论 关系 -- 元组
概念/逻辑 实体 属性 实例
实现 行集、表 列 行
物理 文件 字段 记录

ER模型基本概念

ER 模型的重要性

  • ER：最佳信息模型
    • 能够很快速的向用户展示内部事务的逻辑
  • 启示：把 ER 设计作为数据库设计的第一步

ER 模型的诞生

  • Entity-Relationship Model
  • 1976年，P.P.S.Chen提出 ER 模型，用 ER 图来描述概念模型
  • ER 模型眼中的世界
    • 世界是有一组称作实体的基本对象和这些对象之间的联系构成的

ER 模型中的实体

  • 实体（Entity）
    • 客观存在并可相互区分的事物叫实体
  • 属性（Attribute）
    • 实体所具有的某一特性
    • 一个实体可以由若干个属性来刻画
  • 域（Domain）
    • 属性的取值范围

实体型与实体集

  • 实体型（Entity Type)
    • 实体名 + 属性名集合
    • 实体（值）是实体型的一个特例
    • 抽象的概念
  • 实体集（Entity Set）
    • 同型实体的集合
  • 例子
    • 实体型：学生（姓名、性别）
    • 实体：（张三，男）
    • 实体集：全体学生

ER 模型中的联系

  • 联系（Relationship）
    • 实体之间的相互关联
  • 联系也可以有属性
  • 联系的元（Degree）
    • 参与联系的实体集的个数
    • 一元联系又被称为递归联系
  • 联系是发生在实体集之间的，而不是实体型

例子

  • 联系与联系的元
    • 学生与老师间的授课联系
      • 二元联系
    • 学生与学生间有班长联系
      • 可以是实体集内部的联系
      • 一元联系，只有一个实体集
  • 联系的属性
    • 如学生与课程之间有选课联系，每个选课联系都有一个成绩作为其属性

实体的码（Key）

  • 超码（superkey）
    • 能唯一标识实体的属性或属性组
    • 超码的任意超集也是超码
  • 候选码（candidate key）
    • 其任意真子集都不能成为超码的最小超码
  • 主码（primary key）
    • 从所有候选码中选定一个用来区别同一实体集中的不同实体
    • 一个实体集中任意两个实体在主码上的取值不能相同
    • 选择上一般越简单越好

一个例子

A B C
1 2 3
2 3 4
1 4 5
3 2 6
  • 超码
    • C、AC、BC、ABC、AB
  • 候选码
    • C、AB

如何确定联系的码

  • 联系的种类不一样的时候，联系的码也不一样
  • 例子：实体集 A，实体集 B，AB 之间存在联系 C
    • 如果每个 A 只能和一个 B 发生联系 C
      • 联系的码：实体集 B 中的一个候选码即可
    • 如果每个 A 可以和多个 B 发生联系 C，多个 A 可以与一个相同的 B 发生联系
      • 联系的码：实体集 A 和实体集 B 中的各选一个候选码进行组合

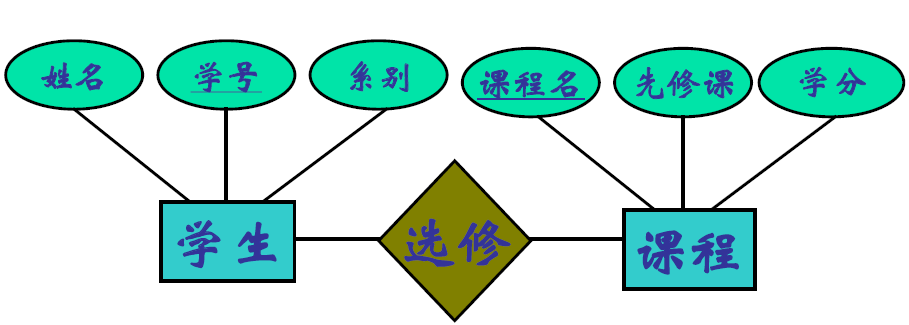
码在 ER 图中的表示

  • 实体集属性中作为主码的一部分的属性用下划线来标明

其他的码

  • 替代码
    • 除去主码之外的候选码
  • 自然码
    • 一个与行中属性有逻辑联系的候选码，它是实体的 “真正的” 属性
  • 代理码
    • 人工码，只起唯一标识作用的序列号，不是实体本身的属性
  • 智能码
    • 经过编码的标识符
    • 例如：身份证

基本 ER 图要点

  • 一个例子：学生选修课程

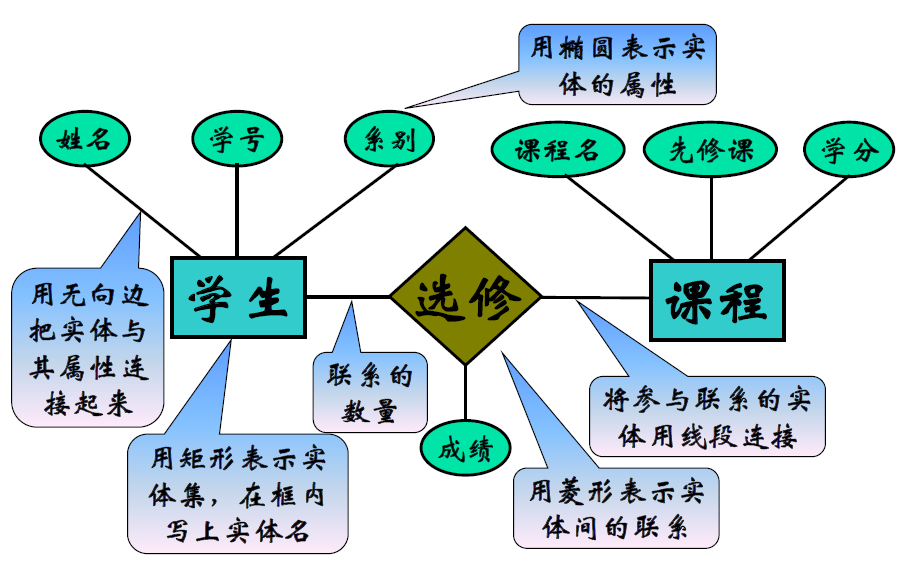
  • 实体集
    • 用矩形表示实体集，在框内写上实体名
  • 实体的属性
    • 用椭圆表示实体的属性
    • 用无向边把实体与其属性连接起来
  • 联系
    • 用菱形表示实体间的联系
    • 将参与联系的实体用线段连接
      • 联系的数量

一些 ER 图的例子

  • 一个实体集只能出现一次
  • 因此实体集内部的联系应该这么表示

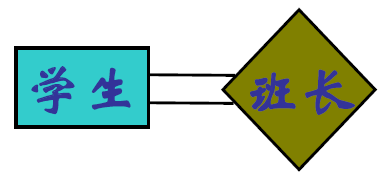
  • ER 图的连通性
    • 连通：可以进行一些探索性的查询
    • 不连通：可以放在独立的数据库里
  • 联系是实体集之间的联系，而不是实体之间的联系

参与

  • 参与（Participation）
  • 实体集之间的关联称为参与，即实体参与联系
  • 例子
    • 王军选修 “数据库基础”
    • 表示实体 “王军” 与 “数据库基础” 参与了联系 “选修”
  • 类型
    • E 全部参与 R
      • 实体集 E 中的每个实体都参与到联系集 R 中的至少一个联系
    • E 部分参与 R
      • 实体集 E 中只有部分实体参与参与到联系集 R 的联系中
  • 一个联系的两个实体集可能一个完全参与，一个部分参与
  • 参与在 ER 图中的表示
    • 用双线连接联系与完全参与的实体

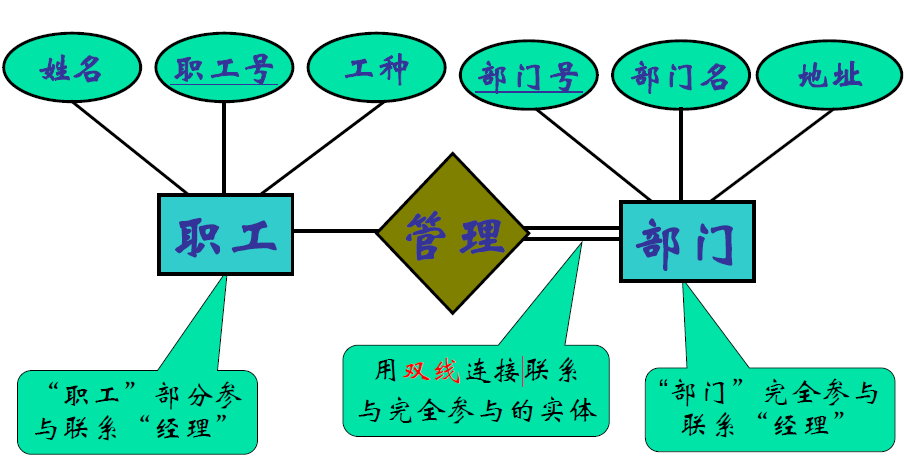
  • 识别联系的参与度有何作用？
    • 在设计关系表时可以确定更优的设计方式
    • 例子：上面的职工、部门之间的管理联系
      • 设计的时候会把管理这个联系放在部门的表里，而不是放在职工的表里
      • 放在职工的表里，空的地方太多

存在依赖

  • 存在依赖（Existence Dependency）
  • x 存在依赖于 y
    • 实体 x 的存在依赖于实体 y 的存在
    • y 称作支配实体
    • x 称作从属实体
    • 如果 y 被删除，则 x 也要被删除
  • 例子

  • 存在依赖必是完全参与
    • 还款存在依赖于贷款，则还款全部参与和贷款之间的属于联系

角色

  • 角色（Role）
  • 实体在联系中的作用称为实体的角色
  • 多元联系中的角色是相对清晰的，一元联系需要显式注明
  • 对于一元联系，为区别各实体参与联系的方式，需要显式指明其角色

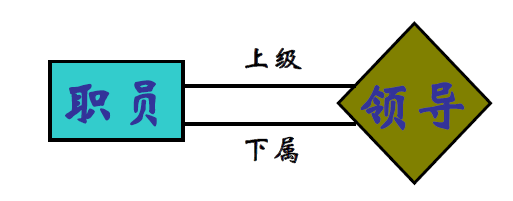
角色在 ER 图中的表示

  • 当需要显式区分角色时，在连接菱形和矩形的线上加上说明性标注以区别不同的角色

属性类型

简单属性与复合属性

  • 简单属性
    • 不可再分的属性
  • 复合属性（Composite）
    • 可以划分为更小的属性
  • 为什么使用复合属性？
    • 把相关属性聚集起来以反映更高层次的概念，可以使模型更清晰
  • 例子

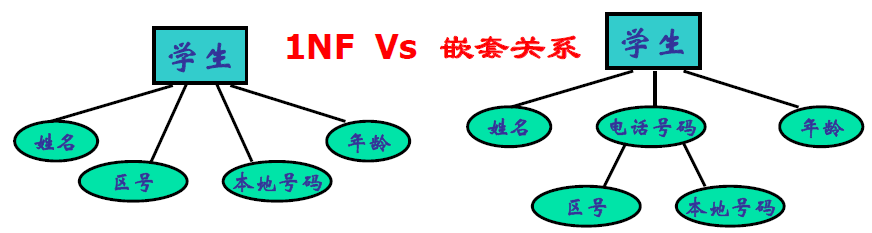
单值属性与多值属性

  • 单值属性
    • 每一个特定的实体在该属性上的取值唯一
  • 多值属性
    • 某个特定实体在该属性上有多于一个的取值
  • 多值属性的问题
    • 拆开成表的时候，会产生冗余（其他的单值属性由于这个多值属性的展开而被多次存储）
    • 一般会单独来存

派生属性与基属性

  • 派生属性（Derived）
    • 可以从其他相关的属性或实体派生出来的属性值
  • 例子：学生的绩点可以由器所选课程的成绩计算出来
    • 绩点为派生属性
    • 成绩为基属性，或存储属性
  • 数据库设计的时候，一般把基属性放在实际的表里，派生属性用视图
    • 只存基属性值，而派生属性只存其定义或依赖关系，用时再从基属性中计算出来

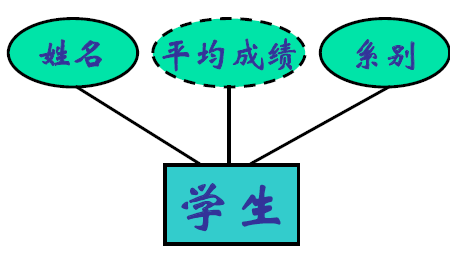
属性在 ER 图中的表示

  • 多值属性用双椭圆表示

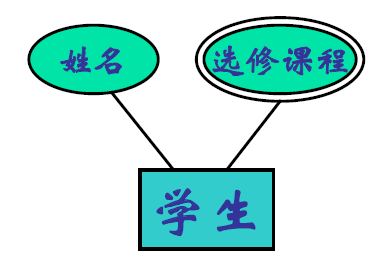
  • 派生属性用虚椭圆表示

NULL 属性

  • null 表示 ”无意义“
    • 当实体在某个属性上没有值时设为 null
    • 表示对于这个实体而言，这个属性是不合适的（不存在这个属性）
  • null 表示 “值未知”
    • 值存在，但目前没有获得该信息
  • 三值逻辑：true、false、unkown
  • 实体完整性要求主码取值不能为 null

联系的基数

联系的种类

  • 实体之间的联系的数量，即一个实体通过一个联系集能与另一实体集相关联的实体的数目
  • 一对一（1：1）
  • 一对多（1：m）
  • 多对多（m：n）

联系种类在 ER 图中的表示

表示 1

  • 用箭头或线段来表示联系的种类，箭头指向单方实体集

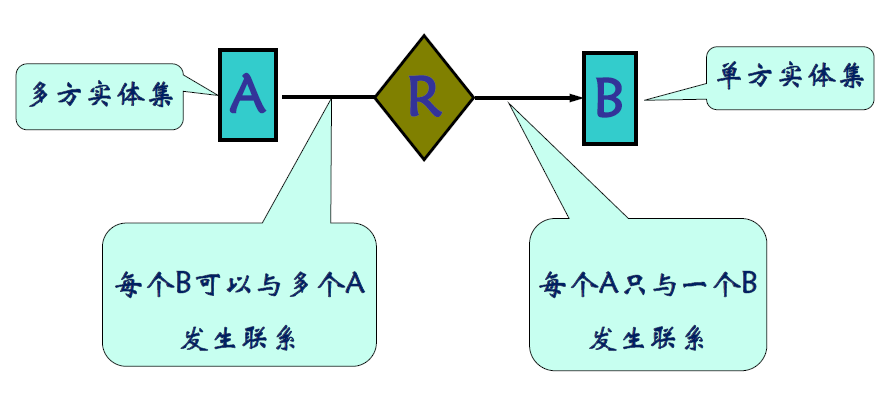
  • 一个解释：A 同学，B 导师
    • 一个学生只能有一个导师
    • 一个导师可以有多个学生

表示 2

  • 多方实体的箭头指向联系集

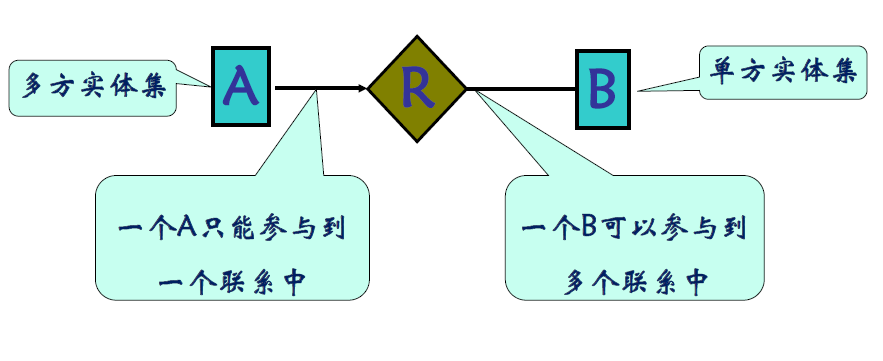
  • 同样的理解
    • 一个同学只能参与到一个联系里面，一个老师可以参与到多个联系里面

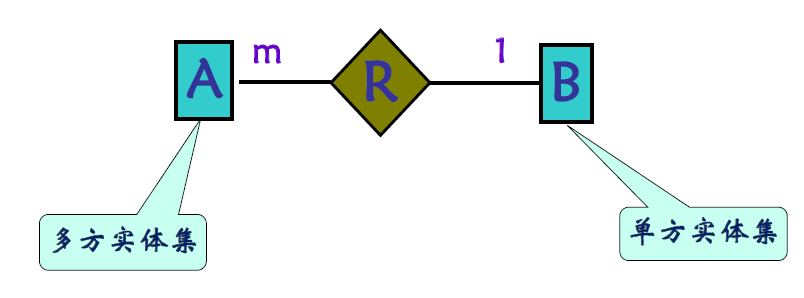
表示 3

  • 在多方实体和联系之间的线段上标注字母
  • 在单方实体和联系之间的线段上标注数字 1

二元联系的种类

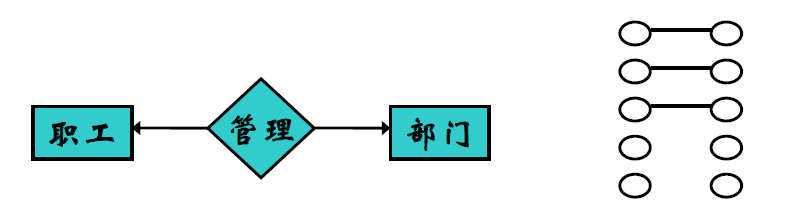
一对一

  • 两个实体集 \(E_1\)、\(E_2\) 之间的一对一联系
  • \(E_1\) 中的一个实体与 \(E_2\) 中至多一个实体相联系，并且 \(E_2\) 中的一个实体与 \(E_1\) 中至多一个实体相联系
  • 一对一不是一一对应
    • 可能有实体集中的实体不参与联系（如下图右边）

一对多

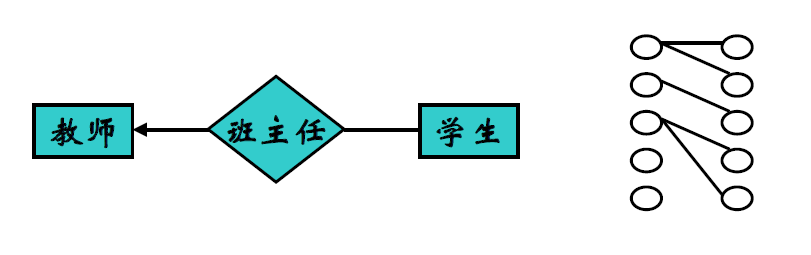
  • 两个实体集 \(E_1\)、\(E_2\) 之间的一对多联系
  • \(E_1\) 中的一个实体与 \(E_2\) 中 \(n(n\ge0)\) 个实体相联系，并且 \(E_2\) 中的一个实体与 \(E_1\) 中至多一个实体相联系

多对多

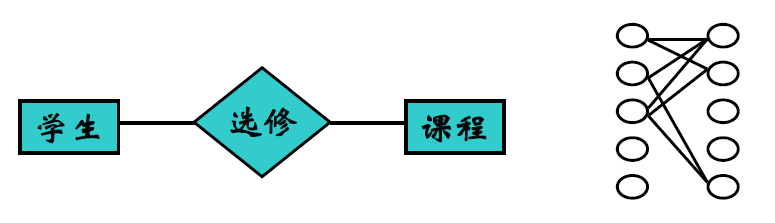
  • 两个实体集 \(E_1\)、\(E_2\) 之间的多对多联系
  • \(E_1\) 中的一个实体与 \(E_2\) 中 \(n(n\ge0)\) 个实体相联系，并且 \(E_2\) 中的一个实体与 \(E_1\) 中 \(m(m\ge0)\) 个实体相联系

一个实体集内的递归联系

  • 一对一
graph RL;
B{配偶};
A[职工];
B --->|妻子| A
B --->|丈夫| A
  • 一对多
graph RL;
B{领导};
A[职工];
B ---|属下| A
B --->|上级| A
  • 多对多
graph RL;
B{构成};
A[零件];
B ---|母零件| A
B ---|子零件| A

多元联系

歧义

  • 如下的 ER 图可能会出现歧义
    • 每个职工只有一个工种
    • 每个职工在每个部门只有一个工种
graph LR;
A[工种];
B[职工];
C{工作};
D[部门];
B --- C;
D --- C;
C ---> A;
  • 修改为二元联系
    • 每个职工只有一个工种
graph LR;
A[工种];
B[职工];
C{工作};
E{分配};
D[部门];
B --- C;
C --- D;
B --- E;
E ---> A;

多元联系中最多允许出现一个箭头

  • 否则可能会有歧义
    • （学生，评估报告），老师
    • （学生，评估报告，项目），老师
graph LR;
A[学生] --- B{指导} ---> C[老师];
D[评估报告] --- B ---> E[项目];

联系的势

  • 势表达了一个实体出现在联系中的次数
graph LR;
A[教师];
B{教授};
C[课程];
A ---|"(0,2)"| B;
B ---|"(1,4)"| C;
  • 0 表示教师可以不教授课程
  • 区分强制性和可选性联系

复合实体

  • 复合实体也称联合实体或桥接实体
  • 过时了
    • 早期由于图模型不能表示多对多的联系而产生的
  • 复合实体
    • 一个 M：N 联系分解成一个 1：M 和一个 1：N
  • 原来的联系
graph LR;
A[学生]---B{选修}---C[课程];
  • 复合实体
    • 由选修这个实体有关系衍生而来