GAMES101.闫令琪.07.材质与外观(Lecture 17)

Posted on 2021-03-21 Edited on 2023-11-18 In CG.GAMES101 Views:

Materials and Appearances, 不同材质的 BRDF, 微表面模型

https://www.bilibili.com/video/av90798049

材质与外观

Materials and Appearances

常见材质

光柱、头发、海浪、布、蝴蝶的鳞片、鱼肉
光线传播和材质紧密相关
Weta 的 Manuka渲染器
- 比较成熟的渲染器
- 支持 40 多种材质

Material == BRDF

材质：反射不同光的方式

漫反射材质

Diffuse / Lambertian Material

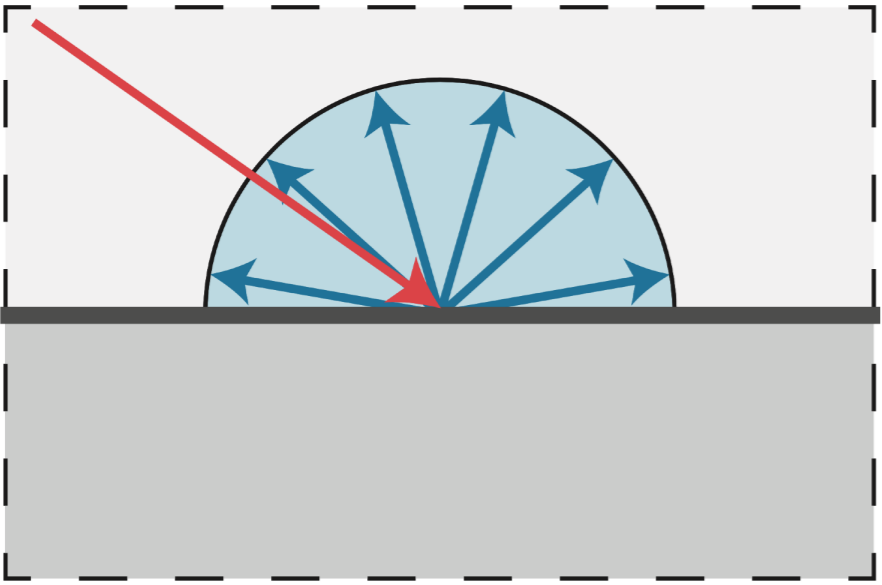
能量守恒：不发光、不吸收光
- 进出的 irradiance 相同
假设入射光在每个方向上均匀分布，出射光也在每个方向上均匀分布，那么就有

\[ L_o=L_i \]

通过 BRDF 得到以下结论

\[ \begin{aligned} L_{o}\left(\omega_{o}\right) &=\int_{H^{2}} f_{r} L_{i}\left(\omega_{i}\right) \cos \theta_{i} \mathrm{d} \omega_{i} \\ &=f_{r} L_{i} \int_{H^{2}} \cos \theta_{i} \mathrm{d} \omega_{i} \\ &=\pi f_{r} L_{i} \end{aligned} \]

\[ f_r=\dfrac{1}{\pi} \]

引入一个反射系数（albedo 反射率）\(\rho\in[0,1]\)，完全不反射 - 完全反射

\[ f_r=\dfrac{\rho}{\pi} \]

Glossy 材质

Glossy material
抛光金属材质
- 有高光，但是高光没那么强

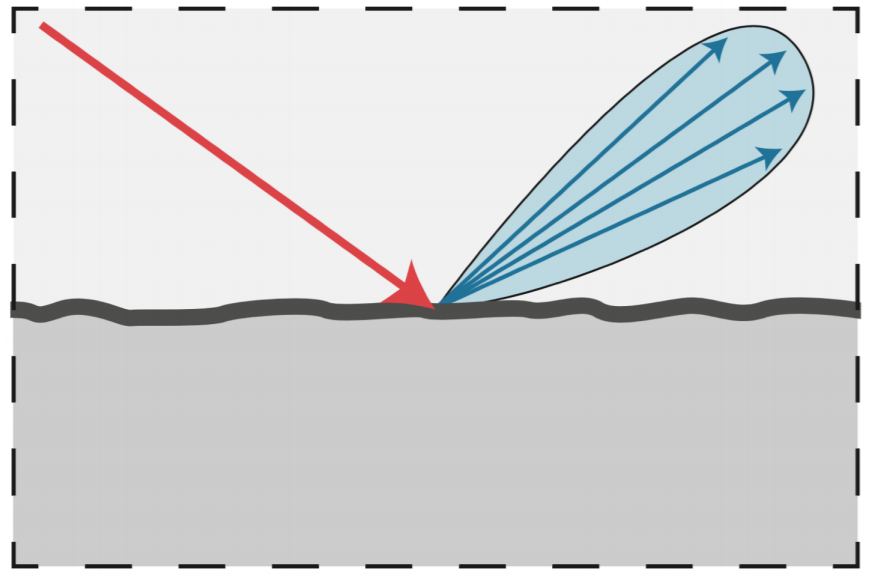
例子

理想反射/折射材质

Ideal reflective / refractive material (BSDF*)
- BSDF： Bidirectional Scattering Distribution Function
  - 双向散射分布函数

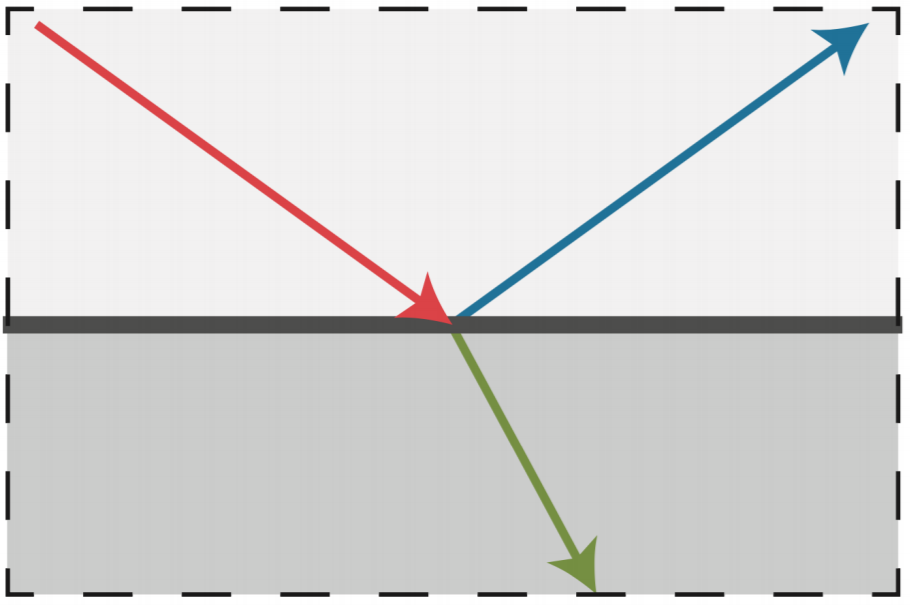
反射光线的计算

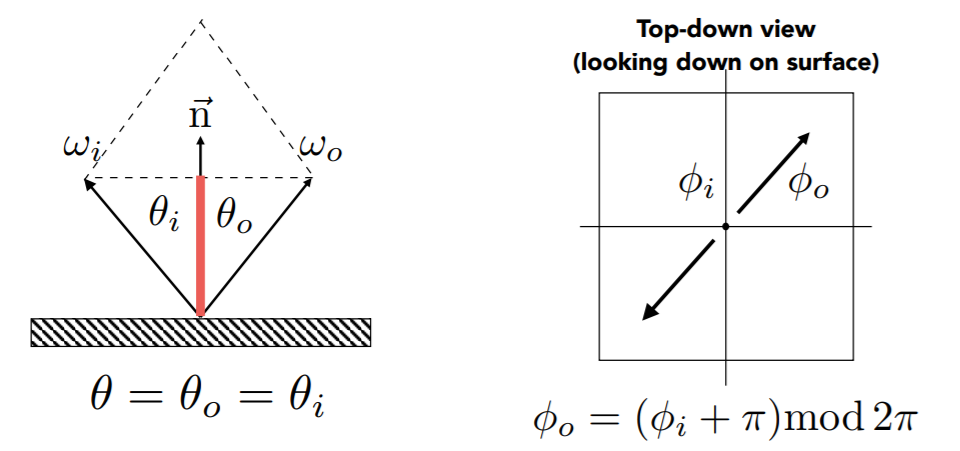
\(\theta\)
- 这里可以看出半角矢量更加好算

\[ \vec{\omega_i} + \vec{\omega_o}=2\cos\theta\ \vec{n}=2(\vec{\omega_i}\cdot\vec{n})\vec{n} \]

\(\phi\)
- 局部坐标系，表面俯视

\[ \phi_o=(\phi_i+\pi)\mod2\pi \]

折射

Specular Refraction
几何光学角度
焦散 caustics

折射定律

Snell' Law

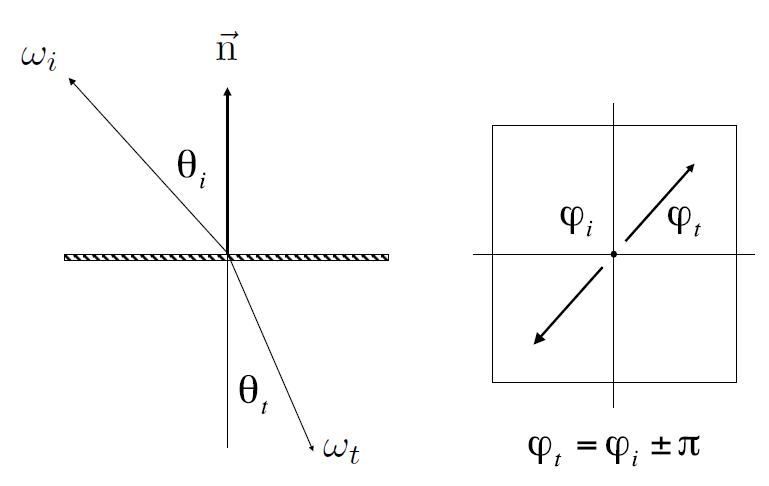
\(\theta\)

\[ \eta_i\sin\theta_i=\eta_t\sin\theta_t \]

\(\phi\)

\[ \phi_o=(\phi_i+\pi)\mod2\pi \]

一些常见介质的折射率

介质 medium	折射率 n
Vacuum（真空）	1.0
Air (sea level)	1.00029
Water (20°C)	1.333
Glass	1.5-1.6
Diamond	2.42

计算折射角的余弦

\[ \begin{aligned} \cos\theta_t&=\sqrt{1-\sin^2\theta_t}\\ &=\sqrt{1-(\dfrac{\eta_i\sin\theta_i}{\eta_t})^2}\\ &=\sqrt{1-(\dfrac{\eta_i}{\eta_t})^2(1-\cos\theta_i)^2}\\ \end{aligned} \]

可能无解：全反射
- \(1-(\dfrac{\eta_i}{\eta_t})^2(1-\cos\theta_i)^2<0\)
- \({\color{red}\eta_i>\eta_t}\)
Snell's Window / Circle
- 水里向上看只能看到一个锥形的区域

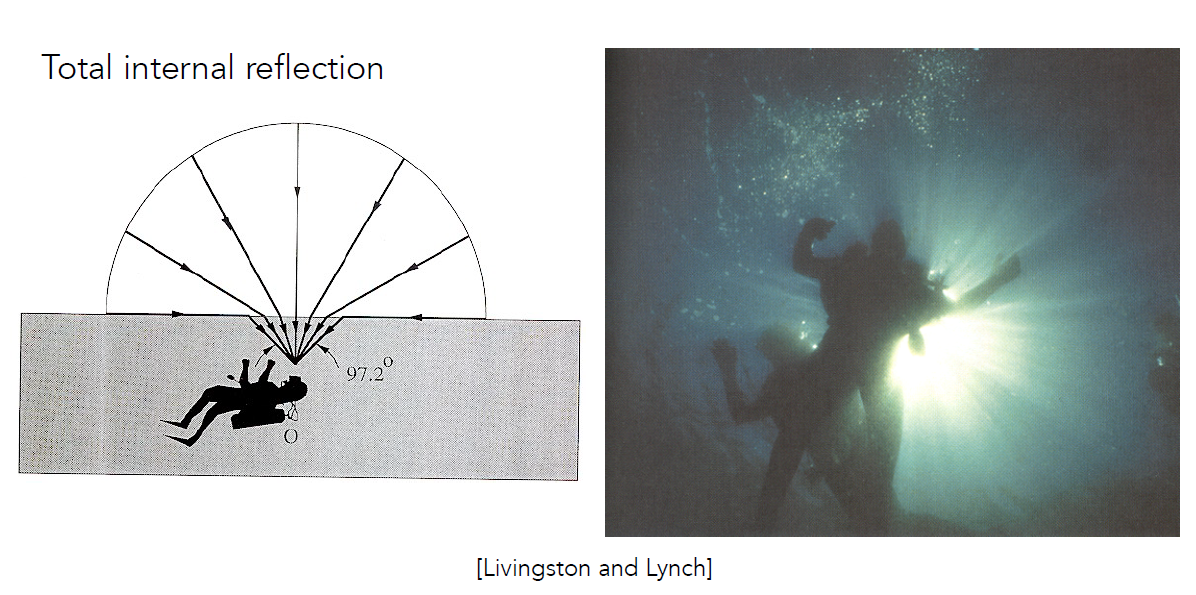
模型中可能发生全反射
对于球体，具有对称性，折射进去的光一定能够折射出来
BSDF = BRDF + BTDF
- 散射 = 反射 + 折射

菲涅尔项

Fresnel Reflection / Term
不同的视角看过去，反射程度不一样

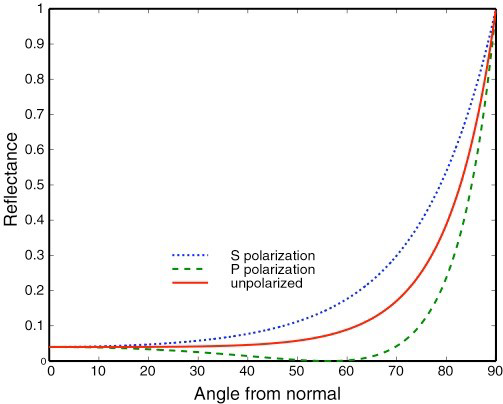
电介质/绝缘体

Dielectric，\(\eta=1.5\)
S，P 两种极化
垂直的时候反射弱

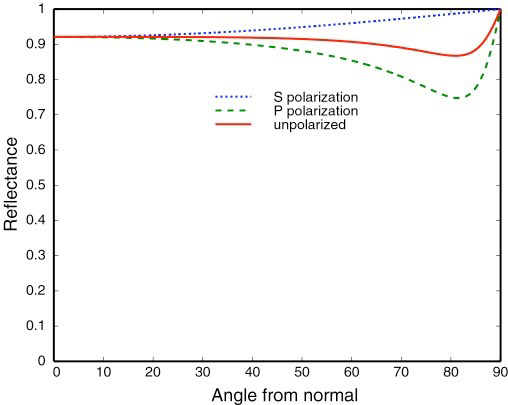
导体

Conductor
垂直的时候也很强
- 古代照镜子用铜镜

精确计算菲涅尔项

需要考虑极化现象

\[ R_s=\left|\dfrac{n_i\cos\theta_i-n_t\cos\theta_t}{n_i\cos\theta_i+n_t\cos\theta_t}\right|^2 \]

\[ R_t=\left|\dfrac{n_i\cos\theta_t-n_t\cos\theta_i}{n_i\cos\theta_t+n_t\cos\theta_i}\right|^2 \]

\[ R_{eff}=\dfrac{R_s+R_t}{2} \]

估计菲涅尔项

Schlick’s approximation
\(\theta:0\to\dfrac{\pi}{2},R(\theta):R_0\to1\)

\[ R(\theta) =R_{0}+\left(1-R_{0}\right)(1-\cos \theta)^{5} \]

\[ R_{0} =\left(\frac{n_{1}-n_{2}}{n_{1}+n_{2}}\right)^{2} \]

微表面模型

Microfacet Material
假设：离得足够远的时候，看不到物体细节，只能看到他们最终对整个表面的作用
微表面理论
Rough surface
- Macroscale: flat & rough
  - 远处看：粗糙的平面
- Microscale: bumpy & specular
  - 近处看：能看出凹凸不平的表面，每一个小的微元都是完全的镜面物体
  - 物理中可用于解释漫反射
    - 表面中有很多微小的镜子，朝向大小各异，最终形成各个方向均匀反射的结果
Individual elements of surface act like mirrors
- Known as Microfacets
- Each microfacet has its own normal

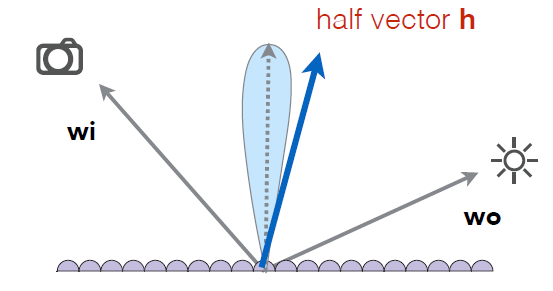
Microfacet BRDF

微表面中法线的分布

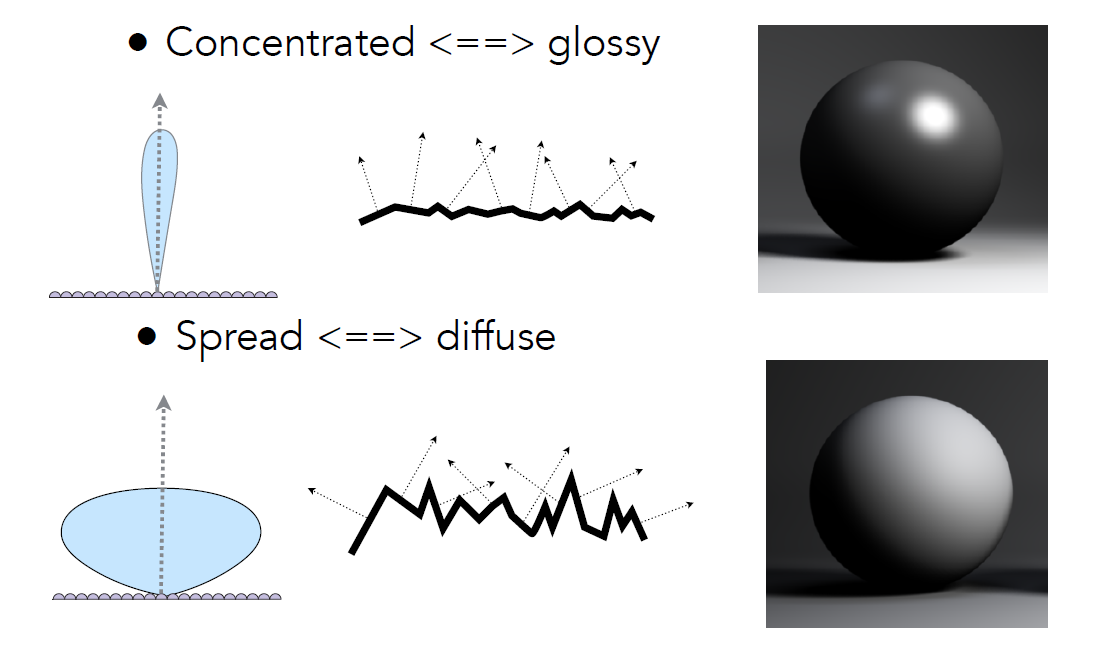
BRDF
- \(\mathbf{F}\)：菲涅尔项（Fresnel term）
- \(\mathbf{G}\)：shadowing-masking term
  - 也称为几何项
  - 微表面的自遮挡
  - grazing angle：几乎和表面方向平行
    - 此时容易发生自遮挡现象
- \(\mathbf{D}\)：表面法线的一个分布
  - 注意微表面时镜面（mirror）
  - 只有半角矢量和法线一致的微表面才能将光线从入射方向传送到出射方向

\[ f(\mathbf{i}, \mathbf{o})=\frac{\mathbf{F}(\mathbf{i}, \mathbf{h}) \mathbf{G}(\mathbf{i}, \mathbf{o}, \mathbf{h}) \mathbf{D}(\mathbf{h})}{4(\mathbf{n}, \mathbf{i})(\mathbf{n}, \mathbf{o})} \]

效果十分强大
基于微表面有很多模型，是一类模型的统称
PBR：Physically Based Rendering / Shading
缺点：Diffuse比较少，有时需要手动加

各向同性/各向异性材质

Isotropic / Anisotropic Materials (BRDFs)
各向同性（Isotropic）：微表面的方向性很弱
各向异性（Anisotropic）：微表面具有一定的方向性

各向异性 BRDF
- 入射角和出射角的相对位置不变（同时仰角不变），方位角发生旋转，结果 BRDF 不同
- Reflection depends on azimuthal angle
  - BRDF 依赖于方位角

\[ f_{r}\left(\theta_{i}, \phi_{i} ; \theta_{r}, \phi_{r}\right) \neq f_{r}\left(\theta_{i}, \theta_{r}, \phi_{r}-\phi_{i}\right) \]

生活中的各向异性材质
- brushed metal
  - 锅底、门把手
- Nylon
- Velvet（天鹅绒）
  - 刷往一个方向（自己人为构造各向异性）

BRDF 的性质

非负性（Non-negativity）
- 是一个分布
线性（Linearity）
- 可加的
可逆性（Reciprocity principle）
- 光路的可逆性
能量守恒（Energy conservation）
- 球面积分小于等于 1（可能有吸收）
各向异性前提下
- 4 维输入变为 3 维的（只和方位角的相对位置有关）

\[ f_{r}\left(\theta_{i}, \phi_{i} ; \theta_{r}, \phi_{r}\right) =f_{r}\left(\theta_{i}, \theta_{r}, \phi_{r}-\phi_{i}\right) \]

\[ f_{r}\left(\theta_{i}, \phi_{i} ; \theta_{r}, \phi_{r}\right) =f_{r}\left(\theta_{i}, \theta_{r}, |\phi_{r}-\phi_{i}\right|) \]

测量 BRDF

动机：
- 菲涅尔项和实际的不太匹配
测量方法

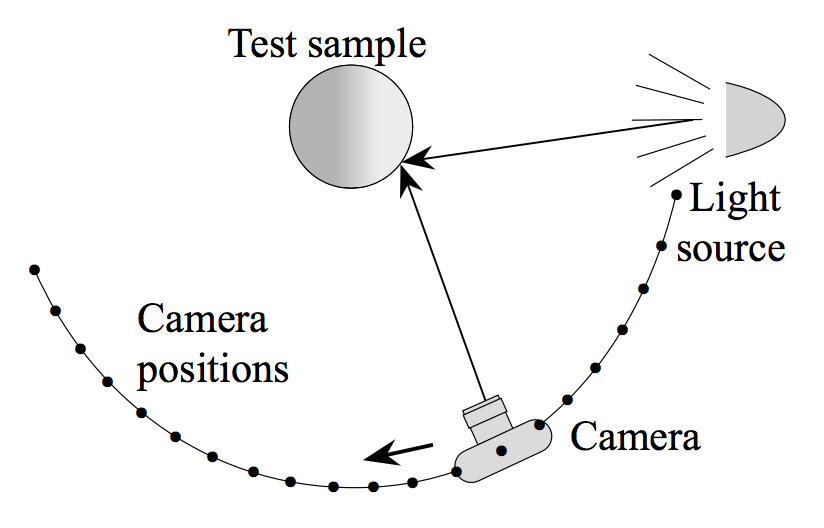
算法

foreach outgoing direction wo
    move light to illuminate surface with a thin beam from wo
    for each incoming direction wi
        move sensor to be at direction wi from surface
    measure incident radiance

降低复杂度
- 各向同性：4D \(\to\) 3D
- 可逆性：减少一半
挑战
- Accurate measurements at grazing angles
  - Important due to Fresnel effects
- Measuring with dense enough sampling to capture high frequency specularities
- Retro-reflection
- Spatially-varying reflectance, ...