GAMES101.闫令琪.06.光线追踪(3).蒙特卡洛路径追踪(Lecture 15-16)

Posted on Edited on In Views:
概率论回顾、解渲染方程、蒙特卡洛路径追踪
  • https://www.bilibili.com/video/av90798049

概率论回顾

  • 随机变量 \(X\)

离散

  • 概率分布函数 \(X \sim p(x)\)
    • Probability Density Function (PDF)
  • 性质
    • \(p_i\ge0\)
    • \(\sum_{i=1}^np_i=1\)
  • 期望 \(E(X)\)
    • \(E[X]=\sum_{i=1}^{n} x_{i} p_{i}\)

连续

  • 概率密度函数 \(X \sim p(x)\)
    • Probability Distribution Function (PDF)
  • 某一个 \(x\) 对应的微元对应的概率 \(p(x)dx\)
    • 长条面积
  • 性质
    • \(p(x)\ge0\)
    • \(\int p(x)dx=1\)
  • 期望
    • \(E[X]=\int x p(x) d x\)

随机变量的函数

  • 如果某个随机变量 \(Y\) 是随机变量 \(X\) 的函数
    • \(Y=f(X)\)
  • 期望的关系
    • \(E[Y]=E[f(X)]=\int f(x)p(x)dx\)

蒙特卡洛积分

  • Monte Carlo Integration
  • 用于求定积分
    • 数值形式是比较难求的定积分
  • 黎曼积分：划分为若干段，每段围成的小矩形之和（极限）

Monte Carlo 积分

  • 定积分 \(\int_a^bf(x)dx\)
  • 随机变量 \(X_i\sim p(x)\)
  • 蒙特卡洛积分 \(F_{N}=\dfrac{1}{N} \sum_{i=1}^{N} \dfrac{f(X_{i})}{p(X_{i})}\)

例子：均匀分布

  • \(X_i\sim p(x)=C\)
    • \(\int_a^bCdx=C(b-a)=1\)
    • \(C=\dfrac{1}{b-a}\)
  • \(F_N=\dfrac{b-a}{N} \sum_{i=1}^{N}f(X_{i})\)

性质

  • 样本越多，越准确
    • The more samples, the less variance.
  • 对 x 采样，只能对 x 做积分
    • Sample on x, integrate on x.

Path Tracing

Whitted-Style Ray Tracing

  • 具体运作
    • Always perform specular reflections / refractions
    • Stop bouncing at diffuse surfaces

问题

  • 不能很好的模拟 Glossy（金属，类似磨砂的感觉） 材质的物体
  • 能产生高光，但是又有点糊，没有那么光滑
  • The Utah Teapot（经典模型）

  • 漫反射物体之间的反射光无法模拟
    • Color Bleeding 效果
      • 右图中盒子的侧面产生红色 / 绿色的效果
  • The Cornell Box（经典模型）
    • 广泛用于测试全局光照

路径追踪

  • 基于渲染方程

\[ L_{o}(p, \omega_{o})=L_{e}(p, \omega_{o})+\int_{\Omega^{+}} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) d \omega_{i} \]

  • 问题
    • 积分：蒙特卡洛方法求解
    • 递归定义

简单的蒙特卡洛方法求积分

  • 忽略发光项

\[ L_{o}(p, \omega_{o})=\int_{\Omega^{+}} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) d \omega_{i} \]

  • 待求的就是上面的方程
  • 蒙特卡洛积分方程

\[ \int_a^bf(x)dx\approx\dfrac{1}{N} \sum_{i=1}^{N} \dfrac{f(X_{i})}{p(X_{i})},X_k\sim p(x) \]

\[ f(x)= L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) d \omega_{i} \]

  • 简单的 PDF
    • 半球立体为 \(2\pi\)

\[ p(\omega_i)=\dfrac{1}{2\pi} \]

  • 积分方程

\[ L_{o}(p, \omega_{o})\approx\dfrac{2\pi}{N} \sum_{i=1}^{N} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) d \omega_{i} \]

  • 根据这个方程，那么就可以得出一个算法
    • 递归算法
1
2
3
4
5
6
7
8
9
10
11
12
shade(p, wo):
    Randomly choose N directions wi~pdf
    Lo = 0.0
    For each wi:
        Trace a ray r(p, wi)
        # 碰到光源, 直接光照
        If ray r hit the light:
            Lo += (1 / N) * L_i * f_r * cosine / pdf(wi)
        # 碰到物体, 间接光照
        Else If ray r hit an object at q:
            Lo += (1 / N) * shade(q, -wi) * f_r * cosine/ pdf(wi)
    return Lo

问题1：指数爆炸

  • 光线数量：\(N^{bounces}\)
  • \(N=1\) 则不会有问题：近似效果会变差
  • 近似效果很差，noisy

解决方案

  • 可以为同一个像素，多次发射光线
    • Trace more paths through each pixel and average their radiance!

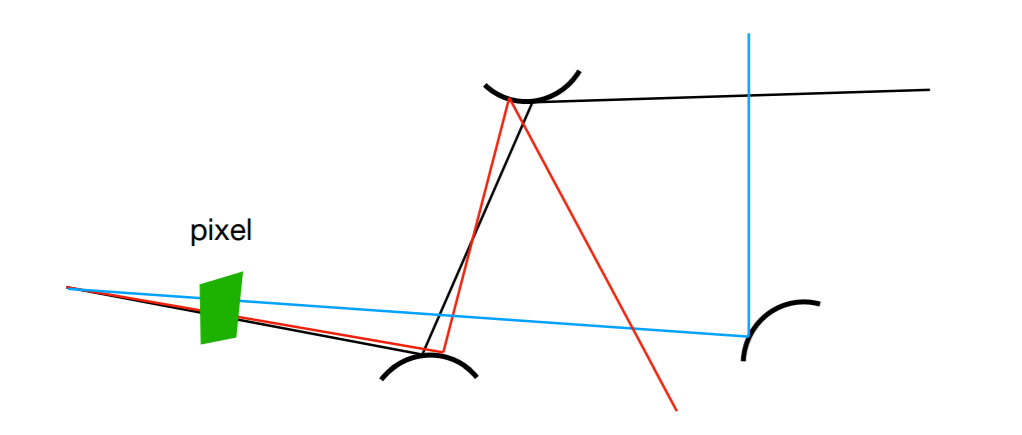
  • Ray Generation
1
2
3
4
5
6
7
8
ray_generation(camPos, pixel):
    Uniformly choose N sample positions within the pixel
    pixel_radiance = 0.0
    For each sample in the pixel:
        Shoot a ray r(camPos, cam_to_sample)
        If ray r hit the scene at p:
            pixel_radiance += 1 / N * shade(p, sample_to_cam)
    return pixel_radiance

问题2：停不下来

  • 互相调用：概率是很小的
  • 事先设置一个递归深度
    • 不行，之前的例子
    • 玻璃灯，当设置的 bounces 比较小的时候，由于光线没有从玻璃外壳内出来，看不到里面的灯
    • 能量损失了
      • Cutting #bounces == cutting energy!

解决方法

  • Russian Roulette（RR）
    • 俄罗斯轮盘赌
  • 一定的概率停止光线追踪
    • 概率 \(p\) 发出一条光线，将得到的结果除以 \(p\)
      • \(\dfrac{L_o}{p}\)
    • 概率 \(1-p\) 不发出光线，得到结果 \(0\)
    • 巧妙的一点：期望还是 \(L_o\)
      • \(E(X)=p\times\dfrac{L_O}{p}+(1-p)*0=L_O\)
  • 伪代码如下（\(N=1\)）
1
2
3
4
5
6
7
8
9
10
11
shade(p, wo):
    Manually specify a probability P_RR
    Randomly select ksi in a uniform dist. in [0, 1]
    If (ksi > P_RR):
        return 0
    Randomly choose ONE direction wi~pdf(w)
    Trace a ray r(p, wi)
    If ray r hit the light:
        return L_i * f_r * cosine / pdf(wi) / P_RR
    Else If ray r hit an object at q:
        return shade(q, -wi) * f_r * cosine / pdf(wi) / P_RR
  • bounces 的期望

\[ \sum_i^{\infty}i(p^{i})(1-p)=\dfrac{p}{1-p} \]

问题3：SSP 小时效果不好

  • SSP：Samples Per Pixels
  • SSP 高的时候，运行很慢

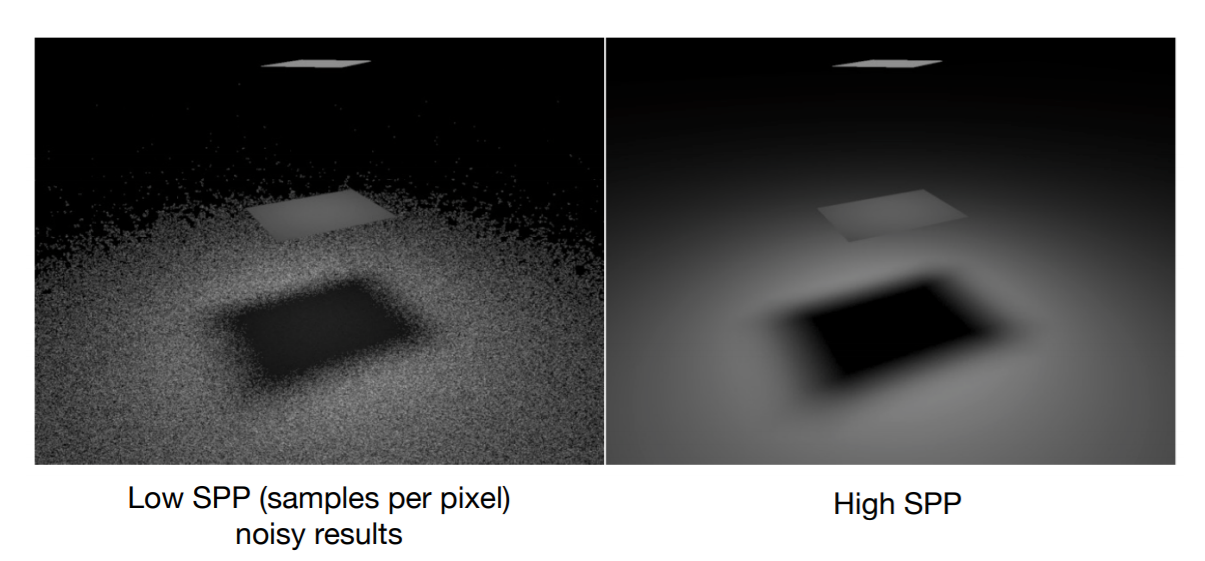
  • 光源比较小的时候，发射出较少的光线很难打到光源

解决方案

  • 修改 PDF
  • 对光源采样

Sampling to the light

  • 对光源均匀采样
  • 面光源面积为 A
    • \(PDF = \dfrac{1}{A}\)
  • 蒙特卡洛方法满足的条件：对谁积分，对谁采样
    • 把渲染方程写成对光源表面的积分
    • 找出 \(dA\) 和 \(d\omega\) 的关系
      • \(dw=\dfrac{dA\cos\theta'}{||x'-x||^2}\)
      • 向球面做投影

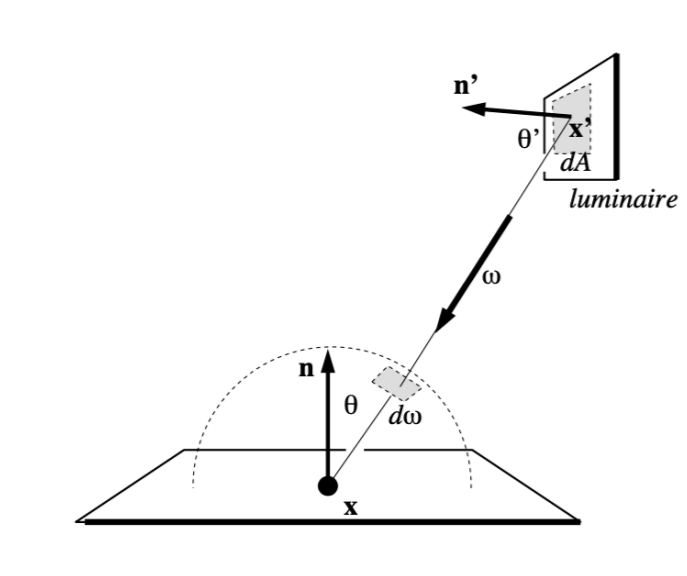
1616070852888

  • 重写渲染方程

\[ \begin{aligned} L_{o}(p, \omega_{o})&=\int_{\Omega^{+}} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) d \omega_{i}\\ &=\int_{A} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) \dfrac{dA\cos\theta'}{||x'-x||^2}\\ &=\int_{A} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})\dfrac{\cos\theta\cos\theta'}{||x'-x||^2}dA\\ \end{aligned} \]

  • 我们将光照分为两个部分
    • light source (direct, no need to have RR)
      • 光源对这个点的共享
    • other reflectors (indirect, RR)
      • 所有其他非光源对这个点的贡献
  • 伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
shade(p, wo):
    # Contribution from the light source.
    # 对光源采样
    Uniformly sample the light at x’ (pdf_light = 1 / A)
    L_dir = L_i * f_r * cos θ * cos θ’ / |x’ - p|^2 / pdf_light

    # Contribution from other reflectors.
    # 对其他物体采样
    L_indir = 0.0
    # 俄罗斯轮盘赌测试
    Test Russian Roulette with probability P_RR
    Uniformly sample the hemisphere toward wi (pdf_hemi = 1 / 2pi)
    Trace a ray r(p, wi)
    # 得判断不是光源
    If ray r hit a non-emitting object at q:
        L_indir = shade(q, -wi) * f_r * cos θ / pdf_hemi / P_RR

    Return L_dir + L_indir
  • 问题：如果光源和待求的点之间有物体
    • 采样点和待求的点之间打一条光线，判断是否会相交
  • 点光源不好处理
    • 做成一个很小的光源

Path Tracing 评价

  • Path tracing (PT) is indeed difficult
    • Consider it the most challenging in undergrad CS
    • Why: physics, probability, calculus（微积分学）, coding
    • Learning PT will help you understand deeper in these
  • Path Tracing 能够做到几乎 100% 真实
    • PHOTO-REALISTIC
    • 照片级的真实感
    • 例子：http://www.graphics.cornell.edu/online/box/compare.html

关于 Ray Tracing 这个概念

  • Ray tracing: Previous vs. Modern Concept
  • 以前
    • 一般指的就是 Whitted 风格的 Ray-Tracing
  • 现代
    • 所有关于光线传播方法的一个大集合
    • (Unidirectional & bidirectional) path tracing
    • Photon mapping
      • 光子映射
    • Metropolis light transport
    • VCM / UPBP…

未涵盖的话题

  • 怎么样在半球上均匀的采样
  • 给一个任何函数，怎么对它进行采样
  • 对于蒙特卡洛采样方法，对于一个函数，怎么选择 PDF 使得最优
    • 重要性采样理论
      • important sampling
    • 用随机数怎么样
      • 随机数有质量之分
      • 好的随机数：均匀分布在空间内，随机数之间的距离也能控制得很好
        • low discrepancy sequences
  • 能不能把对光源和物体的采样结合起来
    • 可以，把不同的采样方法结合起来，使得效果不会比原来的任何一种方法差
    • MIS 采样理论
    • multiple imp. sampling
  • 对于同一个像素的不同 path，简单的做平均行不行，需不需要对靠近中心一点的 path 加一个更大的权
    • pixel reconstruction filter
  • 最终计算出来的是一个 radiance，怎么转化为颜色
    • gamma correction
    • color space
    • HDR（curve）