GAMES101.闫令琪.05.光线追踪(2).辐射度量学(Lecture 14-15)
- https://www.bilibili.com/video/av90798049
辐射度量学
- Basic Radiometry
- Blinn-Phong 模型只是一个近似模型
- 辐射度量学是一个精确模型
- 基于几何光学来做的
- 物理上的准确定义
- 学习思路:WHY, WHAT, HOW
- 一些量的定义
- Radiant Energy,Flux(Power)
- Radiant Intensity,Irradiance, Radiance
- 图形学中很少用能量的概念,都是考虑功率较多
- 能量则需要考虑时间
- 帧一般时间较短
一些物理量的定义
Radiant Energy
- 电磁辐射的能量
- Radiant energy is the energy of electromagnetic radiation. It is measured in units of joules, and denoted by the symbol:
\[ Q\left[J=Joule\right] \]
Radiant Flux / Power
- 功率
- 单位时间的能量
- Radiant flux (power) is the energy emitted, reflected, transmitted or received, per unit time.
\[ \Phi\equiv\dfrac{\mathrm{d}Q}{\mathrm{d}t}\left[W=Watt\right]\left[lm=lumen\right] \]
- 单位:瓦特
- 光学中描述功率:流明
- 灯泡多亮
- 另外的定义
- Flux – #photons flowing through a sensor in unit time
- 单位时间通过的光子数量
一些感兴趣的量
- Radiant Intensity,Irradiance, Radiance
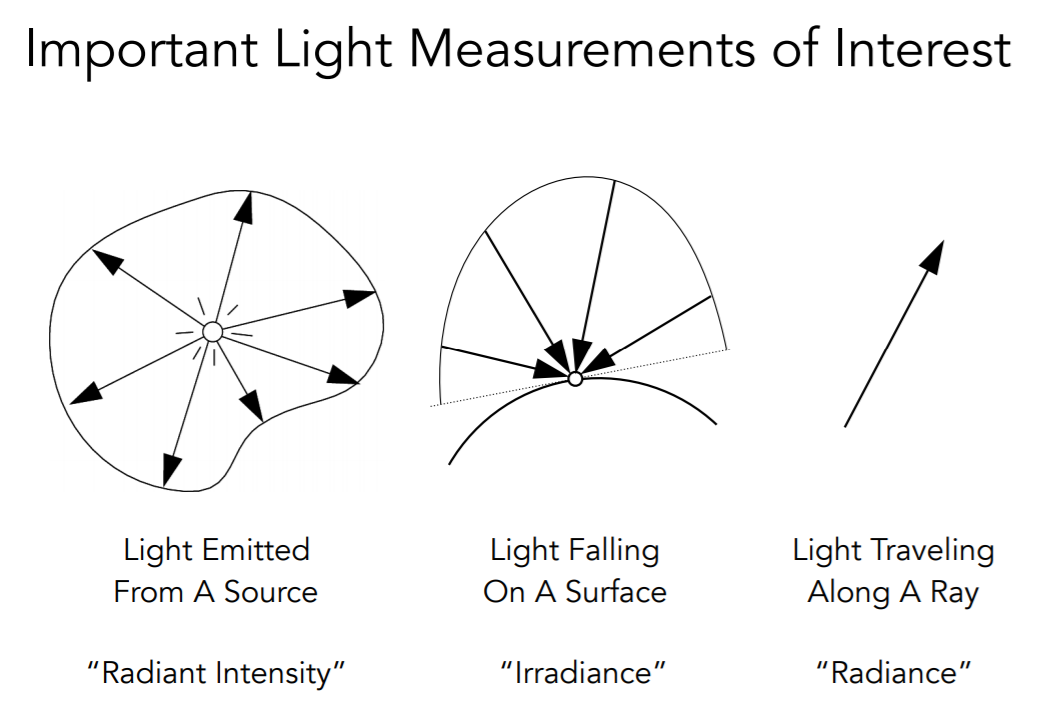
Radiant Intensity
- The radiant (luminous) intensity is the power per unit solid angle emitted by a point light source.
- 单位立体角的 power(flux)
\[ I(\omega)\equiv\dfrac{\mathrm{d}\Phi}{\mathrm{d}\omega}\left[\dfrac{W}{sr}\right]\left[\dfrac{lm}{sr}=cd=candela\right] \]
- sr:立体角的单位
- The candela is one of the seven SI base units.
- 坎德拉:基本单位之一
立体角
- 球面面积占球面表面积的比例 x 一个常数,二维弧度制的延伸
- A:投影到球面上的面积
\[ \Omega=\dfrac{A}{r^2} \]
- 整个球的立体角:\(4\pi\)

- 微分立体角
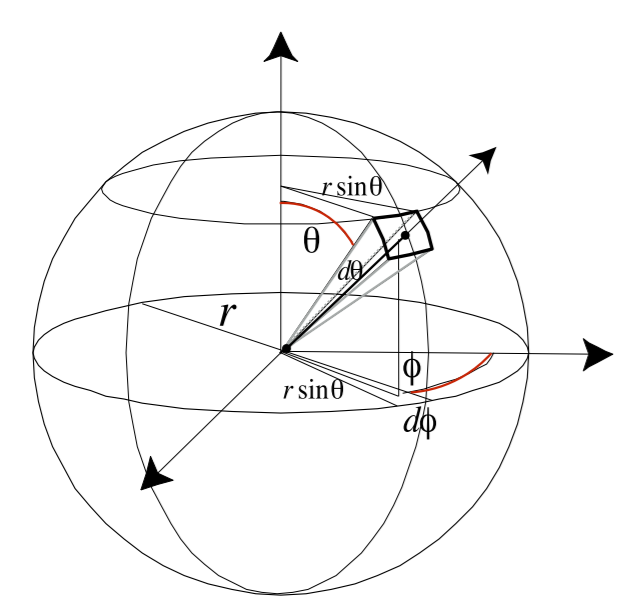 \[
dA=r\sin\theta d\phi\cdot rd\theta=r^2\sin\theta \;\mathrm{d}\theta
\;\mathrm{d}\phi
\]
\[
dA=r\sin\theta d\phi\cdot rd\theta=r^2\sin\theta \;\mathrm{d}\theta
\;\mathrm{d}\phi
\]
- 此时立体角
\[ d\omega=\dfrac{dA}{r^2}=\sin\theta d\theta d\phi \]
- 球的立体角
\[ \Omega=\int_{S^2}\mathrm{d}w=\int_0^{2\pi}\int_0^{\pi}\sin\theta \;\mathrm{d}\theta \;\mathrm{d}\phi=4\pi \]
- 各向同性点光源
- Isotropic Point Source
\[ \Phi=\int_{S^2}I\;\mathrm{d}\omega=4\pi I \]
\[ I=\dfrac{\Phi}{4\pi} \]
- LED 灯:标识的多少瓦实际上表示和白炽灯相比等价于多少瓦
- 标 60W 的 LED 灯实际开销只有 11W
Irradiance
- 无方向性
- 单位面积的 power
- The irradiance is the power per unit area incident on a surface point
\[ E(x)\equiv \dfrac{d\Phi(x)}{\mathrm{d}A}\left[\dfrac{W}{m^2}\right]\left[\dfrac{lm}{m^2}=lux\right] \]
- 光线不垂直于面的时候,需要投影到垂直方向
- 一个例子:四季的产生
- 解释现象
- Blinn-Phong 模型中漫反射的计算
- 光线的衰减
- Intensity 没有衰减,Irradiance 在衰减
Radiance
- 有方向性
- 描述光线
- The radiance (luminance) is the power emitted, reflected, transmitted or received by a surface, per unit solid angle, per projected unit area
\[ L(p,\omega)\equiv\dfrac{\mathrm{d}^2\Phi(p,\omega)}{\;\mathrm{d}\omega \;\mathrm{d}A \cos\theta}\left[\dfrac{W}{sr\ m^2}\right]\left[\dfrac{cd}{m^2}=\dfrac{lm}{sr\ m^2}=nit\right] \]
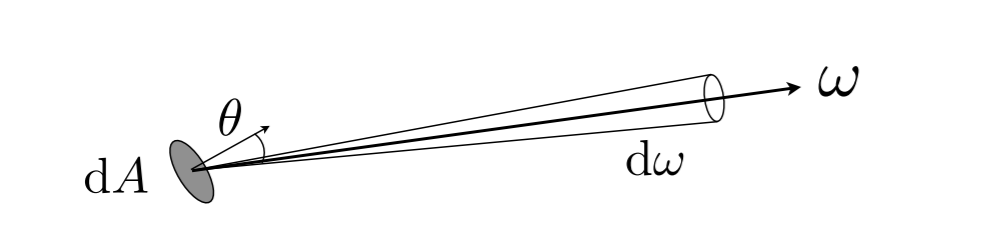
- \(\mathrm{d}A\):发射光的面积
- \(\cos\theta\):投影
- 联系
- Radiance: Irradiance per solid angle
- Radiance: Intensity per projected unit area
Incident Radiance
- it is the light arriving at the surface along a given ray (point on surface and incident direction)
\[ L(p,\omega) = \dfrac{\mathrm{d}E(p)}{\mathrm{d}\omega\cos\theta} \]
Exiting Radiance
- for an area light it is the light emitted along a given ray (point on surface and exit direction)
\[ L(p,\omega) = \dfrac{\mathrm{d}I(p,w)}{\mathrm{d}A\cos\theta} \]
Irradiance 和 Radiance 的关系
- Radiance 在 Irradiance 的基础上增加了方向性
- 某个点接受/发射光线总能量:Irradiance
- 某个点从某个方向接受/向某个方向发射光线能量:Radiance
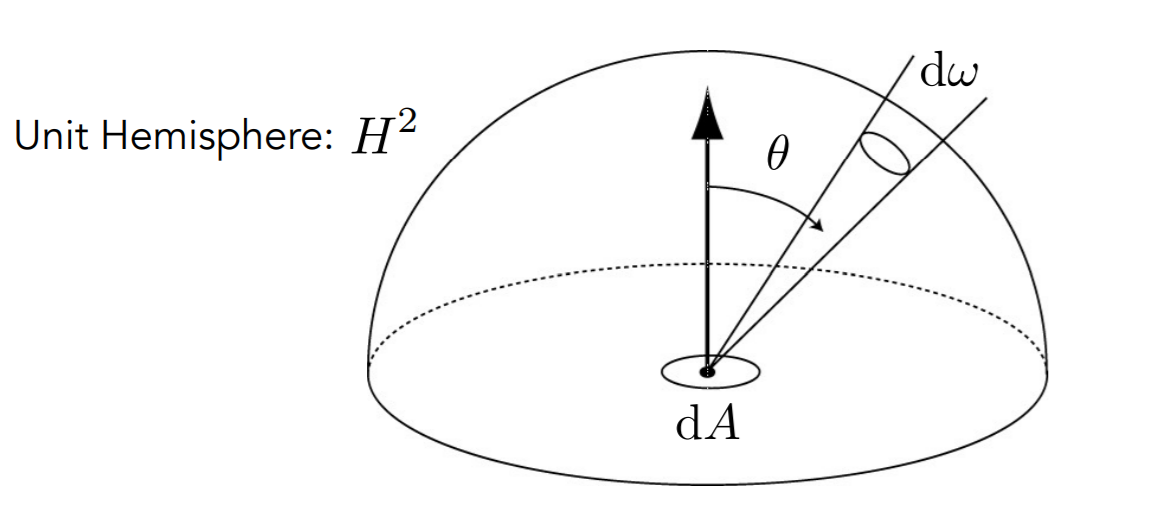
\[ \begin{array}{c} \mathrm{d}E(p,\omega)=L_i(p,\omega)\cos\theta \;\mathrm{d}\omega\\ E(p,\omega)=\int_{H^2}L_i(p,\omega)\cos\theta \;\mathrm{d}\omega\\ \end{array} \]
BRDF
- Bidirectional Reflectance Distribution Function
- 双向反射分布函数
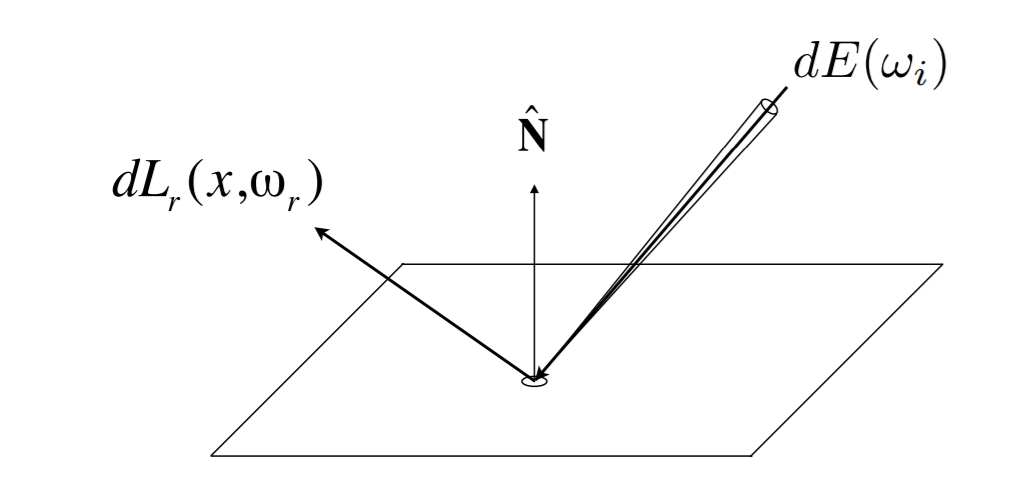
- 进入的 irradiance:\(dE(\omega_i)=L(\omega_i)\cos\theta_i d\omega_i\)
- 出去的 radiance(某个特定方向):\(dL_r(\omega_r)\)
- The BRDF represents how much light is reflected into each
outgoing direction from each incoming
direction
- 是一个比例
\[ f_{r}(\omega_{i} \to \omega_{r})=\frac{d L_{r}(\omega_{r})}{d E_{i}(\omega_{i})}=\frac{d L_{r}(\omega_{r})}{L_{i}(\omega_{i}) \cos \theta_{i} d \omega_{i}}\left[\frac{1}{\mathrm{sr}}\right] \]
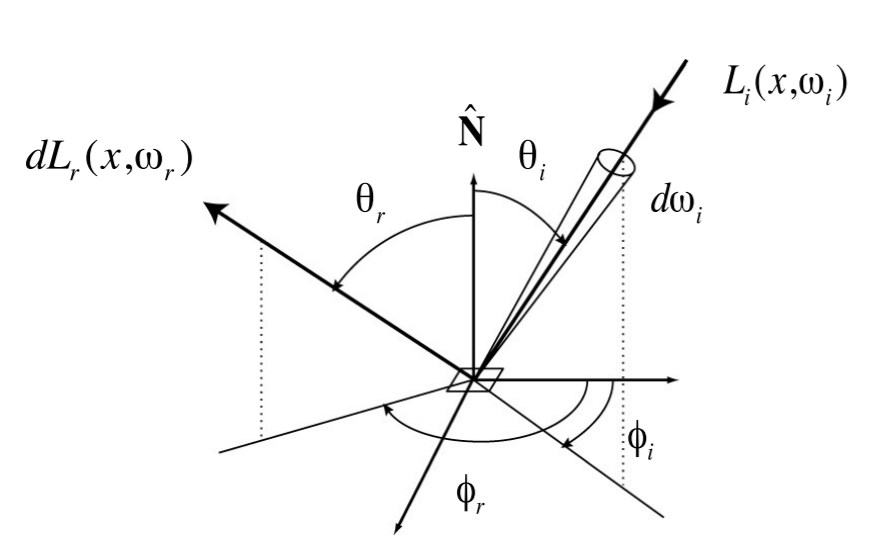
- BRDF 定义了物体的材质
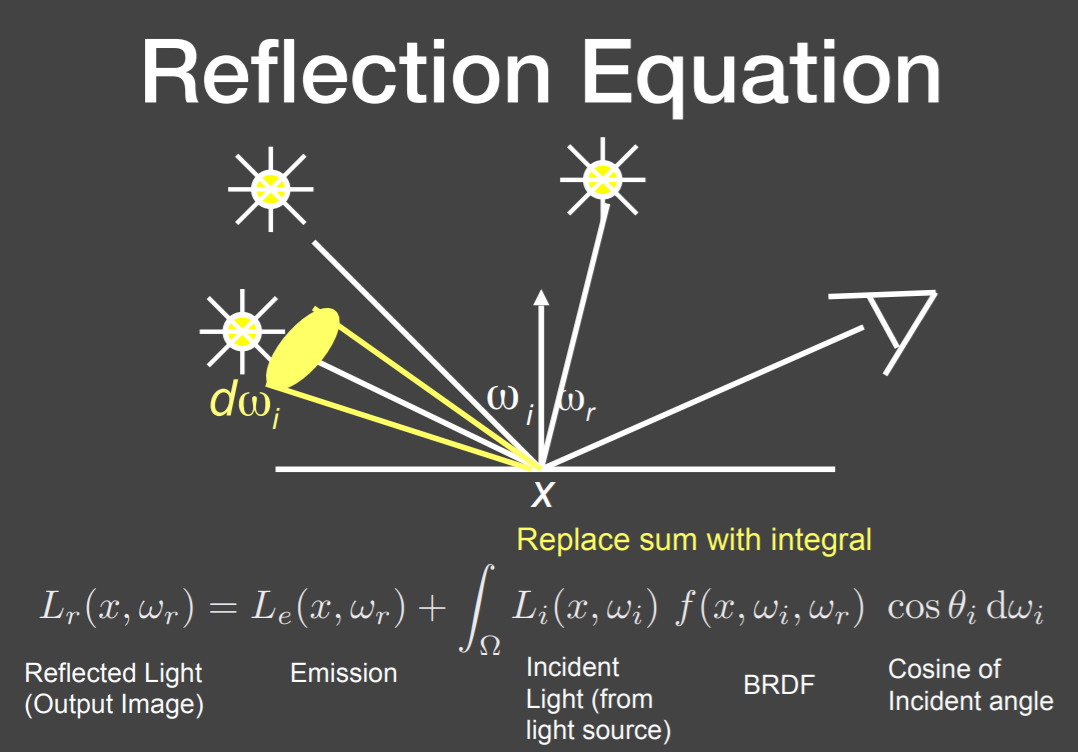
反射方程
- 对所有的入射方向求积分
\[ L_{r}\left(p, \omega_{r}\right)=\int_{H^{2}} f_{r}\left(p, \omega_{i} \rightarrow \omega_{r}\right) L_{i}\left(p, \omega_{i}\right) \cos \theta_{i} \;\mathrm{d} \omega_{i} \]
- \(p\):入射点
- \(\omega_r\):出射方向
- \(\omega_i\):入射方向
渲染方程
- Rendering Equation (Kajiya 86)
- 加上自己的发光成分
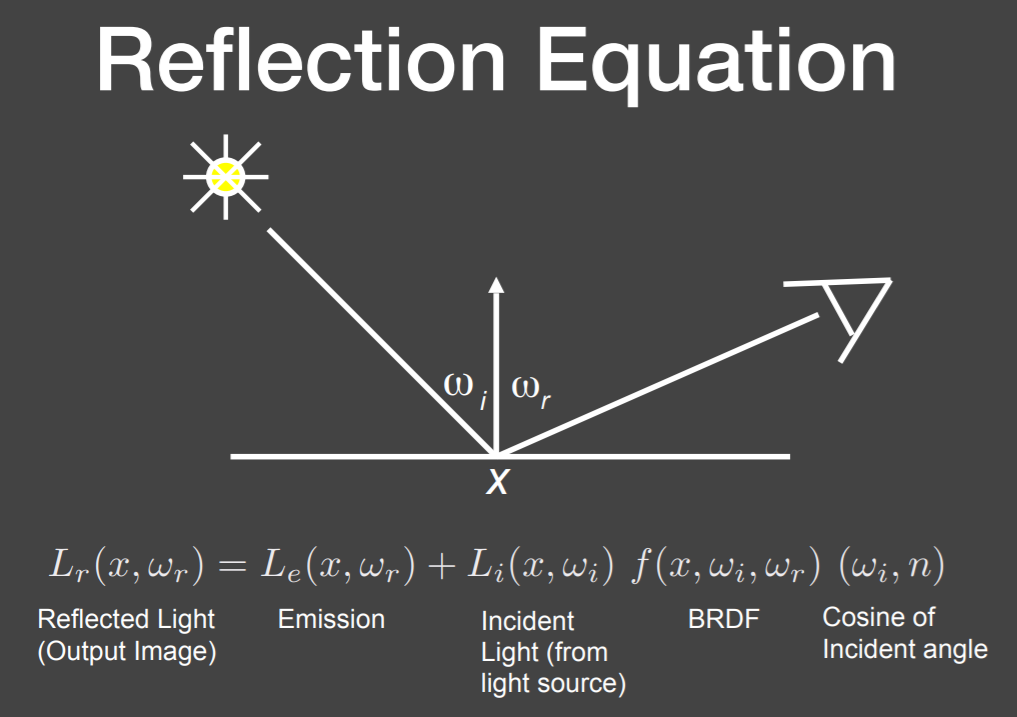
\[ L_{o}(p, \omega_{o})=L_{e}(p, \omega_{o})+\int_{\Omega^{+}} L_{i}(p, \omega_{i}) f_{r}(p, \omega_{i}, \omega_{o})(n \cdot \omega_{i}) \;\mathrm{d} \omega_{i} \]
反射方程到渲染方程
点光源
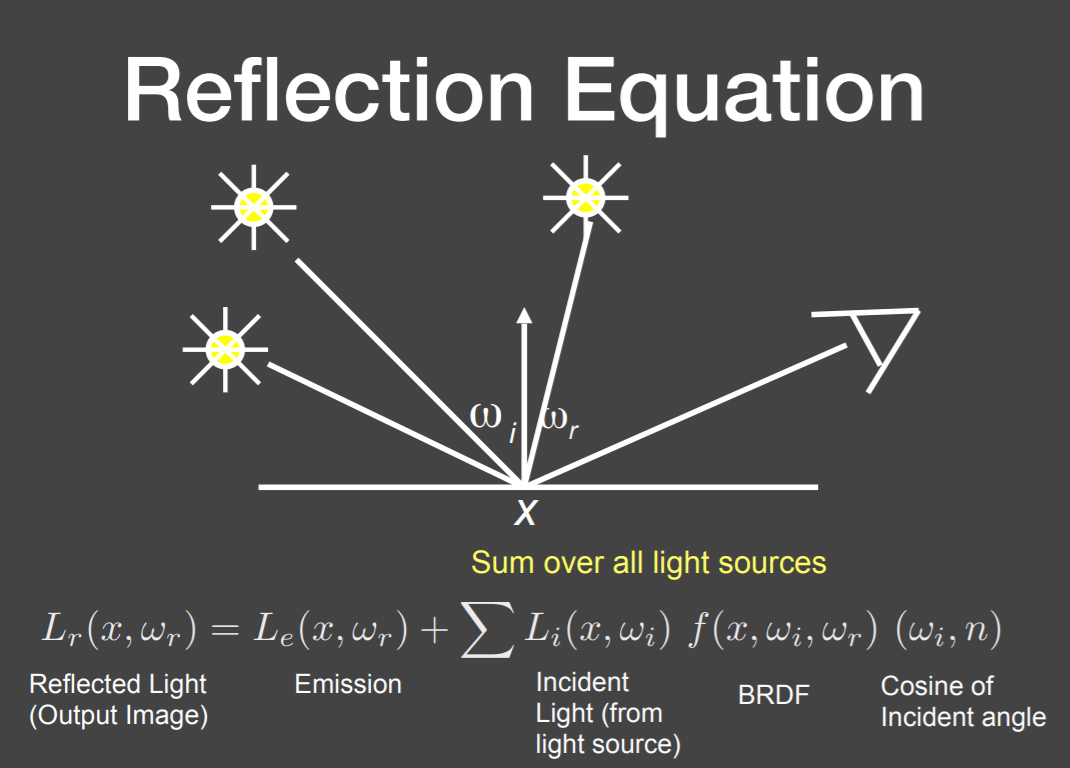
多个光源
- 求和
面光源
- 积分
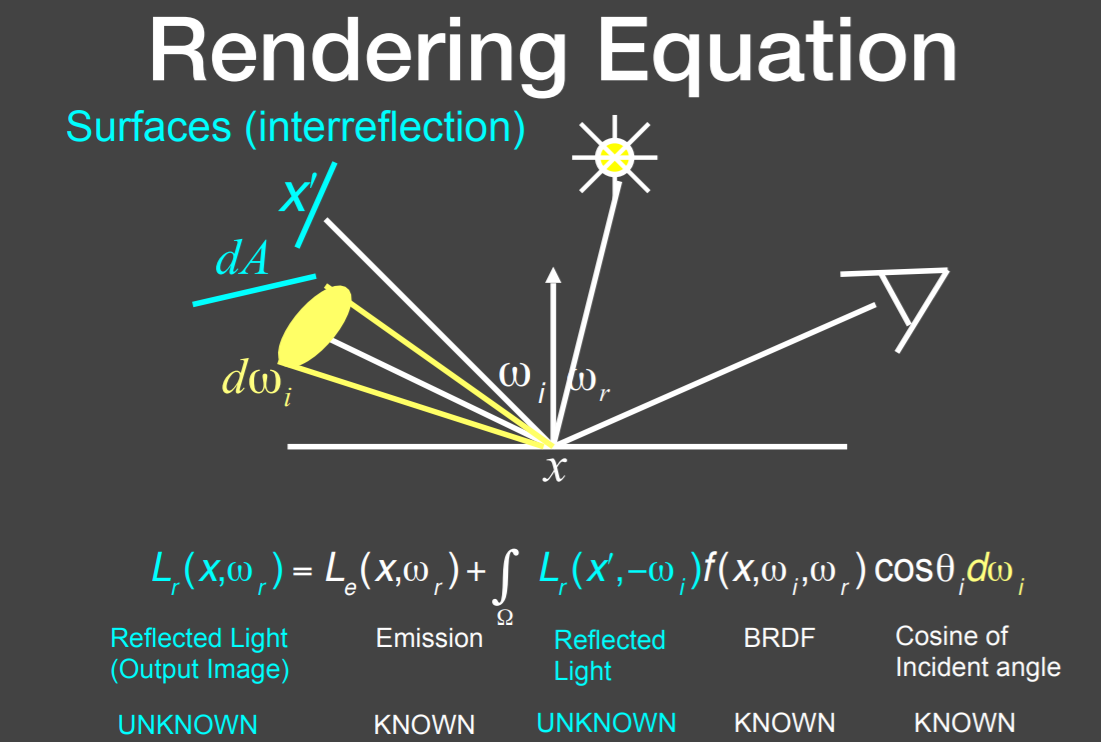
渲染方程
- 间接光照
- 把物体当成是光源
- 现在解渲染方程,相当于求解 \(L\)
Integral Equation
- 渲染方程转化为积分方程
\[ I(u)=e(u)+\int l(v)K(u,v)\;\mathrm{d}v \]
- \(K(u,v)dv\):Kernel of equation Light Transport Operator
Linear Operator Equation
- 通过算符的抽象还可极度简化成如下形式
\[ L = E + KL \]
- 解渲染方程
\[ L=(I-K)^{-1}E \]
\[ L=(I+K+K^2+K^3+K^2+\cdots)E \]
- \(E\):自发光
- \(KE\):直接光照
- \(KE^2\):one-bounce indirect
- 光栅化着色:\(E+KE\)
- 全局光照:直接和间接光照的集合
- 光线跟踪的结果次数增加
- 会收敛到一个亮度
- 能量守恒