GAMES101.闫令琪.04.光线追踪(1).Whitted 风格的光线追踪(Lecture 13-14)

Posted on Edited on In Views:
Whitted 风格的光线追踪，光线和物体求交、加速结构、包围盒
  • https://www.bilibili.com/video/av90798049

光栅化的问题

  • 不好去表示一些全局的效果（Global Effects）
  • 软阴影（Soft Shadow）
    • 光栅化 VSM
  • Glossy Reflection
    • Glossy：有高光的效果，但是同时本身具有粗糙性的材质
  • 间接光照（Indirect Illumination）
    • light bounce more than once
    • 光栅化有一些效果可以模拟，但是效果不太好
  • 光栅化方法
    • 快，但是是一种近似算法
    • Real-Time
  • 光线追踪方法
    • 准确，但是慢
    • Offline（离线）

Ray Tracing

光线的 3 个假定

  • Light travels in straight lines (though this is wrong)
    • 光沿直线传播
  • Light rays do not “collide” with each other if they cross (though this is still wrong)
    • 光线发生交互的时候互不干扰
  • Light rays travel from the light sources to the eye
    • (but the physics is invariant under path reversal - reciprocity).
    • 光线（光路）的可逆性

Ray Casting

  • Appel 1968 - Ray casting
    • Generate an image by casting one ray per pixel
      • 对每个像素，从视点向像素发出一条光线（reciprocity）
    • Check for shadows by sending a ray to the light
      • 对于找到的点，判断其是否处在阴影中（对光源可见）
  • 其他的假设
    • 视点就是一个点
  • 投射光线
    • eye ray：从眼睛射向像素的光线

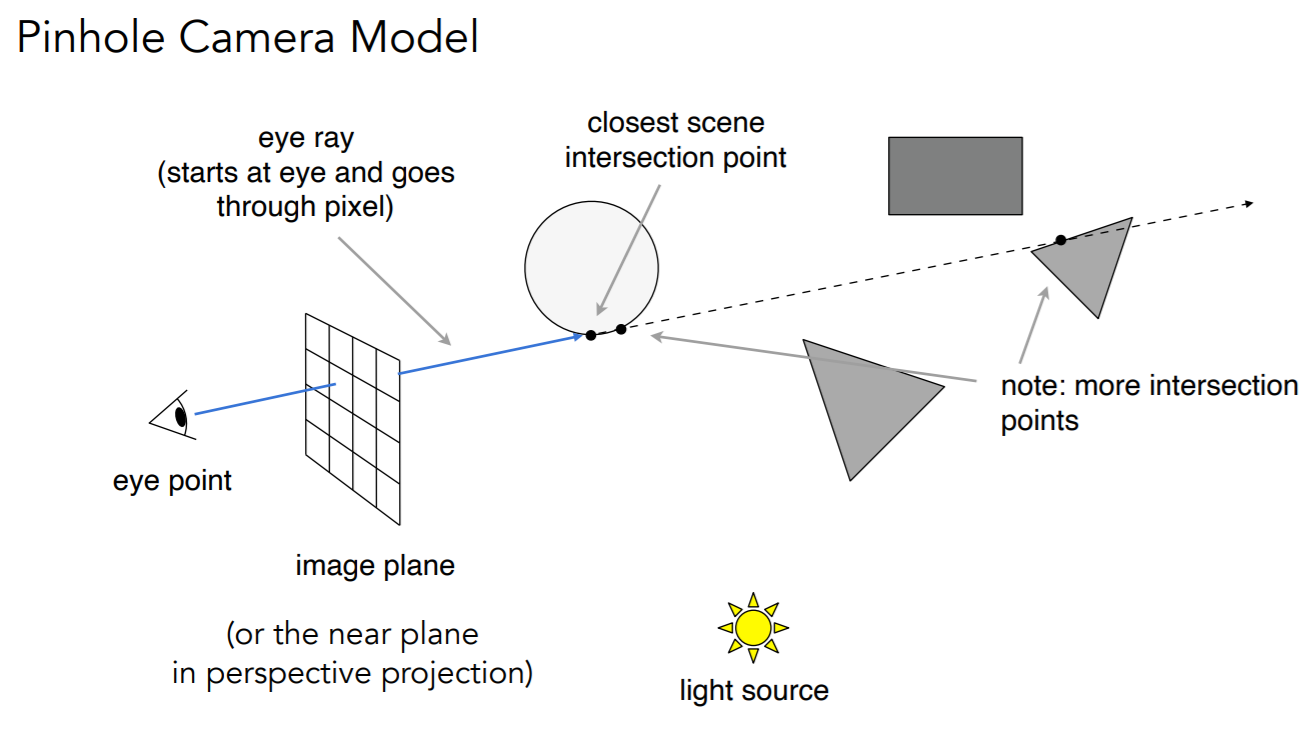
  • 判断是否可见，若可见利用之前的模型进行计算光照

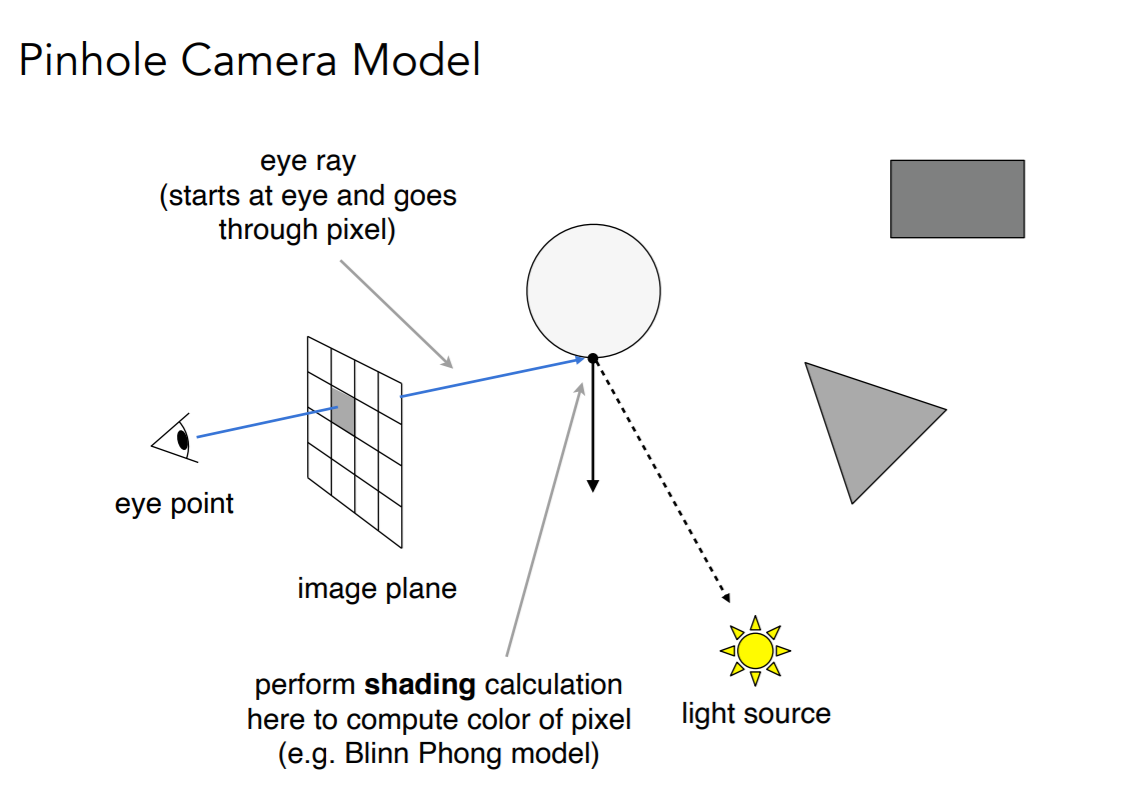
Recursive (Whitted-Style) Ray Tracing

  • 考虑第一次接触点的折射、反射
    • 递归计算
    • shadow rays（判断是否对光源可见）
    • 着色计算：对每一个接触点进行计算
      • 多条光路的叠加
    • 需要考虑能量损失
  • eye ray 又被称为 primary ray
  • secondary ray：经过一次折射/反射之后的线

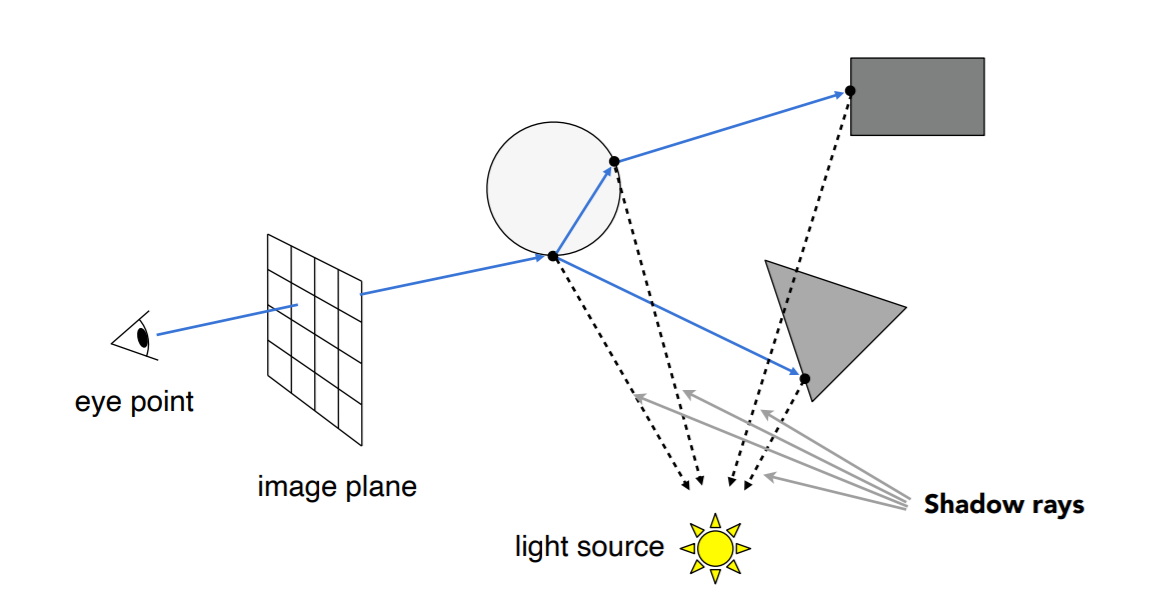
光线求交

  • Ray-Surface Intersection
  • 光线的定义
    • 光线的起点 \(\mathbf{o}\)
    • 光线的方向 \(\mathbf{d}\)
      • 单位向量
  • 光线的方程
    • Ray Equation
    • \(\mathbf{r}(t)=\mathbf{o}+t\mathbf{d},0\le t\le \infty\)

光线与球体求交

  • Sphere
    • \(\mathbf{p}:(\mathbf{p}-\mathbf{c})^2-R^2=0\)
  • 联立方程组求解即可
    • 解的个数：\(0,1,2\)
    • 不相交，相切，两个交点（取小的）

一般的曲面

\[ \left\{ \begin{array}{**lr**} \mathbf{r}(t)=\mathbf{o}+t\mathbf{d},0\le t\le \infty\\ f(\mathbf{p})=0 \end{array} \right. \]

显式表面求交

  • 和三角形求交
  • 可以用于判断点是否在物体内部
    • 内部的点，引一条射线，和物体的交点必为奇数个
    • 外部的点，引一条射线，和物体的交点必为偶数个
  • 很慢，每个三角都需要求交

光线和三角形求交方法

  • 光线和三角形所在的平面求交
  • 判断这个交点是否在三角形内部
  • 平面的定义
    • 法线 \(\mathbf{N}\)
    • 平面上任意一个点 \(\mathbf{p'}\)
  • 平面上的一个点 \(\mathbf{p}:(\mathbf{p'}-\mathbf{p})\cdot\mathbf{N}=0\)
    • 展开后和平面方程相同 \(ax+by+cz+d=0\)
  • 联立方程组求解

Moller Trumbore Algorithm

  • 怎么直接把结果解出来用于判断
  • 重心坐标

\[ \mathbf{r}(t)=\mathbf{o}+t\mathbf{d}=(1-b_1-b_2)\mathbf{P_0}+b_1\mathbf{P_1}+b_2\mathbf{P2} \]

\[ \begin{aligned} &0\le t\le \infty\\ &0\le b_1\le1\\ &0\le b_2\le1\\ &0\le 1-b_1-b_2\le1\\ \end{aligned} \]

  • 3 个未知量，3 个方程（3维）
  • 解的显式表达

加速求交

  • Accelerating Ray-Surface Intersection
  • 如果不加速，算法复杂度
    • pixels x triangles x bounces

Bounding Volumn

  • 包围盒：包围整个模型
  • 先对包围盒求交，如果无交点，则不需要对模型求交
  • 简单的包围盒：长方体
    • 三个对面
    • box is the intersection of 3 pairs of slabs

AABB

  • Axis-Aligned Bounding Box
    • 轴对齐包围盒
    • 计算快
  • 如何计算 （2D 的例子）
    • 每个对面求交
    • \(t_{enter}=\max\{t_{min}\},t_{exit}=\min\{t_{max}\}\)
    • 思想
      • The ray enters the box only when it enters all pairs of slabs
        • 三个对面都进入，才是进入
      • The ray exits the box as long as it exits any pair of slabs
        • 离开一个对面，即离开

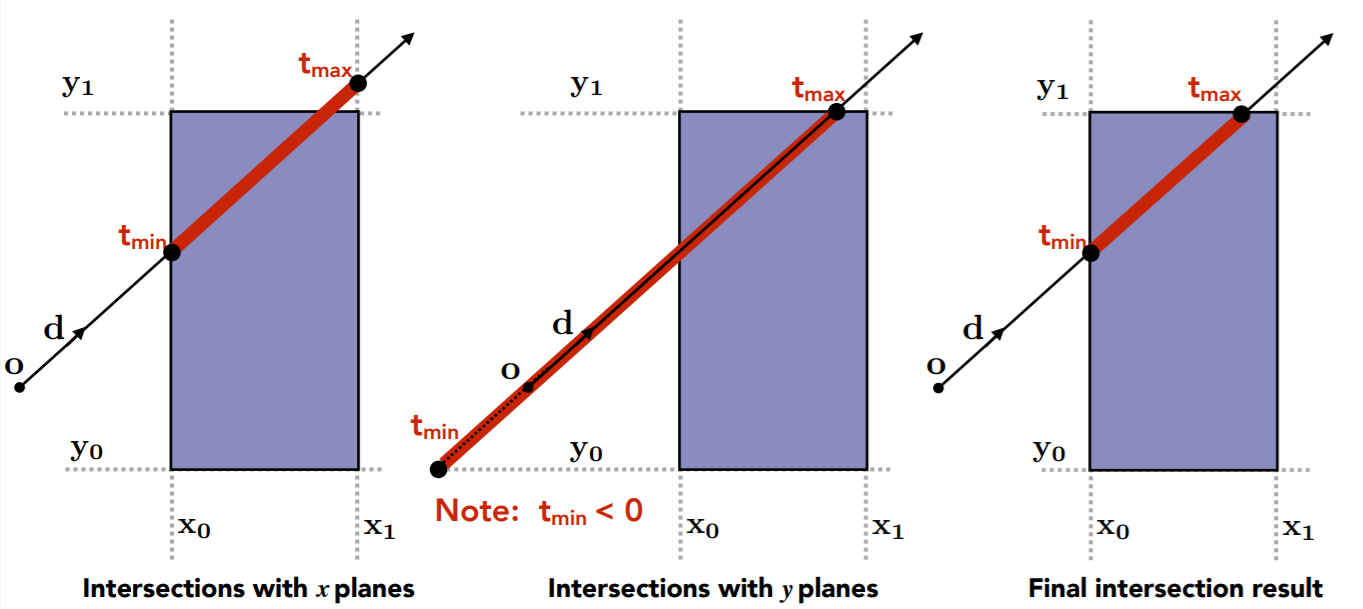
  • 如果不相交：\(t_{exit}\le t_{enter}\)
  • 光线是射线，考虑 \(t\) 的正负
    • \(t_{exit}<0\)：无交点（物体在光线背后）
    • \(t_{enter}<0,t_{exit}\ge0\)：光源在物体里面

GTC 一些新闻

  • GTC news: DLSS 2.0
    • https://zhuanlan.zhihu.com/p/116211994
  • GTC news: RTXGI
    • https://developer.nvidia.com/rtxgi

基于 AABB 的光线求交加速结构

  • 光线与 AABB 求交

均匀的格子

  • Uniform Spatial Partitions (Grids)
  • 场景预处理
    • 网格化
  • 算法步骤
    • 光线与沿途每个盒子求交
    • 若盒子里面含有物体，则于保存的物体部分求交
    • 没有物体，则光线前进（找下一个盒子）

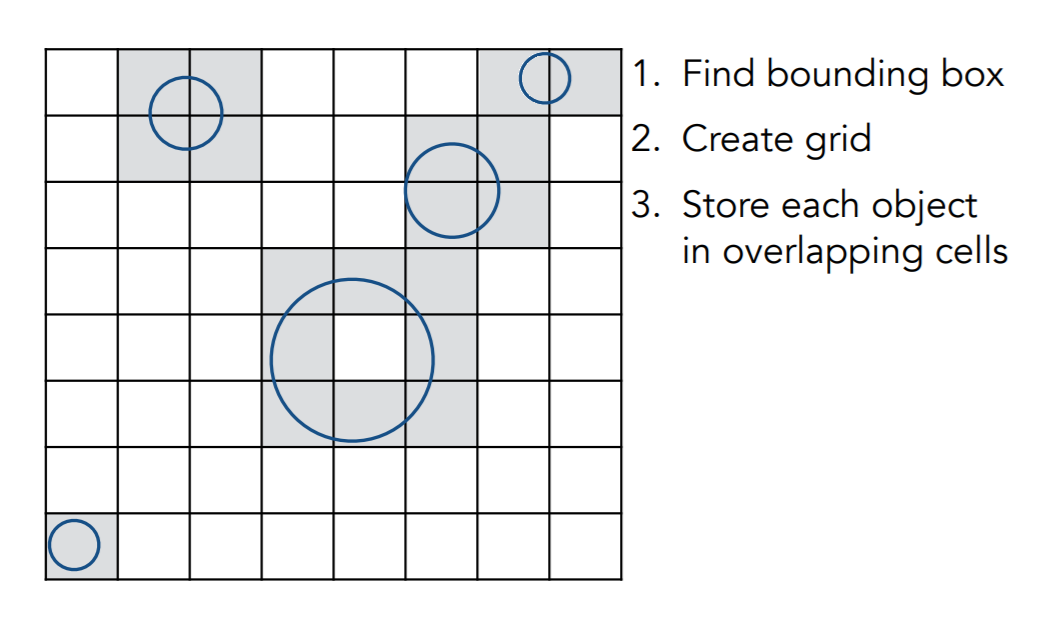
  • 基于想法如下
    • 光线和盒子求交比光线与物体求交快
  • 光线与盒子求交
    • 怎么找光线下一次相交的盒子
      • 最朴素的想法：周围两个都算一遍（向前 2 个测试，向后的 2 个不用管）
    • 高级算法：类似于光栅化一条线的算法

加速程度

  • 网格：1 x 1（无加速效果）
  • 网格过于密集：与盒子求交的成本变大
  • 经验性划分
    • #cells = C x #objs
    • C = 3 x 3 x 3
  • 适合场景
    • 物体多，在场景中分布均匀
  • 不适合场景
    • 场景较空，分布不均匀
      • 大规模空白，和物体相交前需要经过大量空白
    • "Teapot in a stadium" problem

空间划分

  • Spatial Partitions
  • 划分方法
    • 八叉树
      • 维度相关（\(2^n\) 叉树）
    • KD 树
      • 每次只沿着一个轴展开（二叉树）
      • 横竖交划分（相对均匀）
    • BSP 树
      • 空间二分
      • 每次选择一个方向做划分
      • 不是横平竖直的
        • 维度高了就不好计算

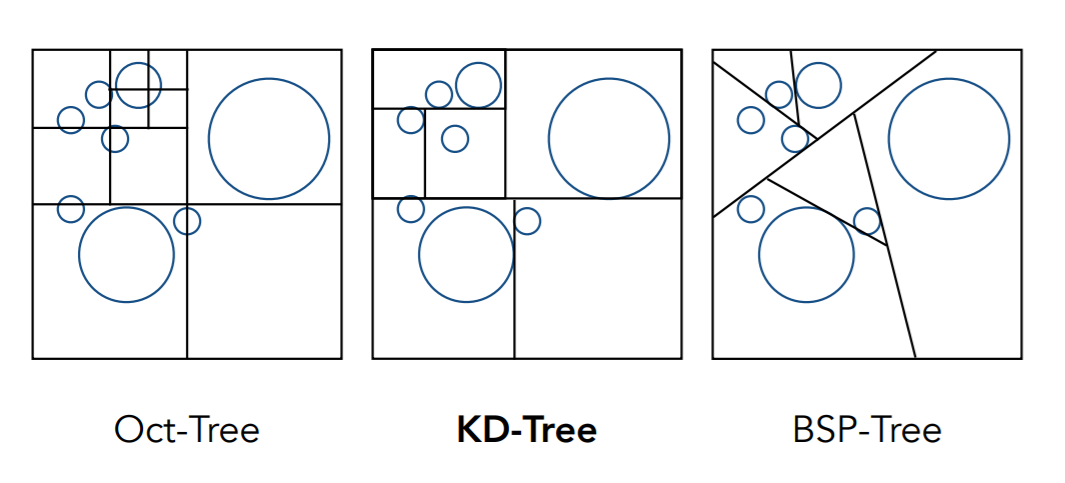
1615975085492

KD-Tree

  • 在光线跟踪之前先建立 KD 树
  • 数据结构
    • 内部结点
      • 记录划分方向（x，y，z）
      • 记录划分位置（不一定是正中间）
      • 子结点（指向子节点的指针）
      • 不需要存储物体信息
    • 外部结点（叶结点）
      • 存储物体列表
  • 光线遍历
    • 先判断和 A 是否有交点
    • 有交点，接着和 A 的两个子结点判断是否有交点
    • 1 有交点，但是是叶子结点了，计算光照
      • 其实 1 还需要继续划分
        • 内部还有多个物体，可能规则上认为可以停止
      • 但是这里已经当作叶子结点了，就不划分了
    • B 有交点，重复上述步骤，进入 B

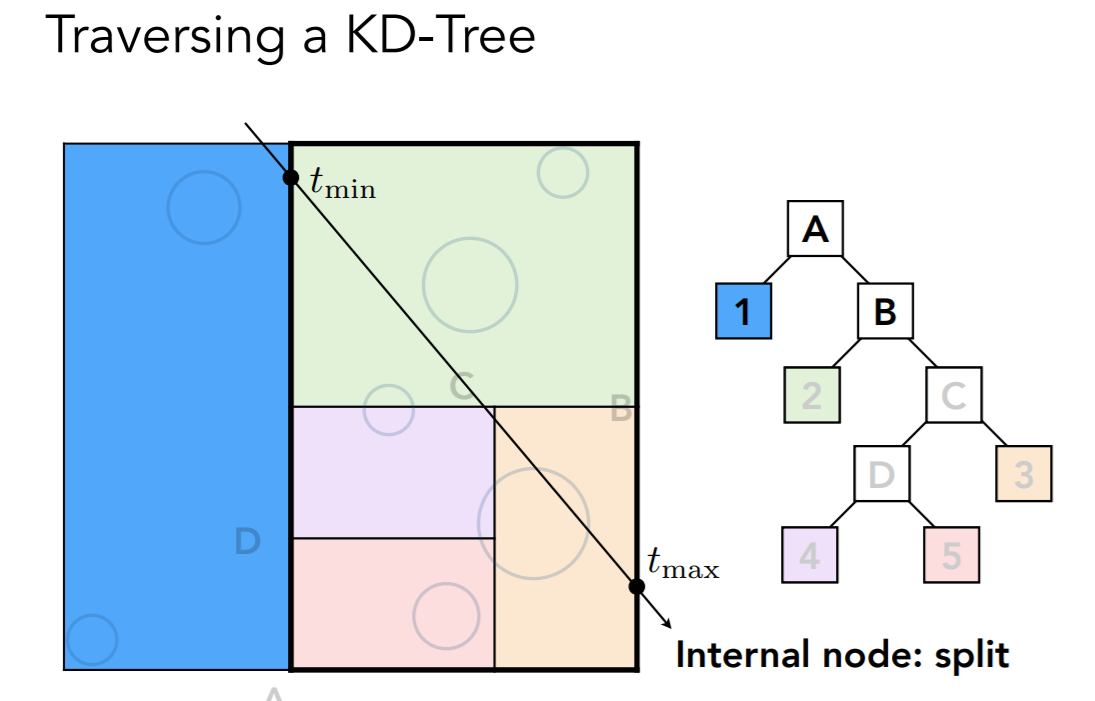
  • 无交点的块不需要计算光照了

存在的问题

  • KD-Tree 的建立不简单
  • 难以判断一个三角形和某个包围盒有交集
    • 3 个顶点都在包围盒外也可能有交点
      • 包围盒穿透三角形
      • 截面整个在三角形内部
  • 一个在边界的物体可能属于多个包围盒
    • 多个叶子节点里面都需要计算光照
  • 现在很少用这种方法了

BVH

  • Bounding Volumn Hierarchy
  • 基于物体的划分
  • Object Partition
  • 现在常用的方法
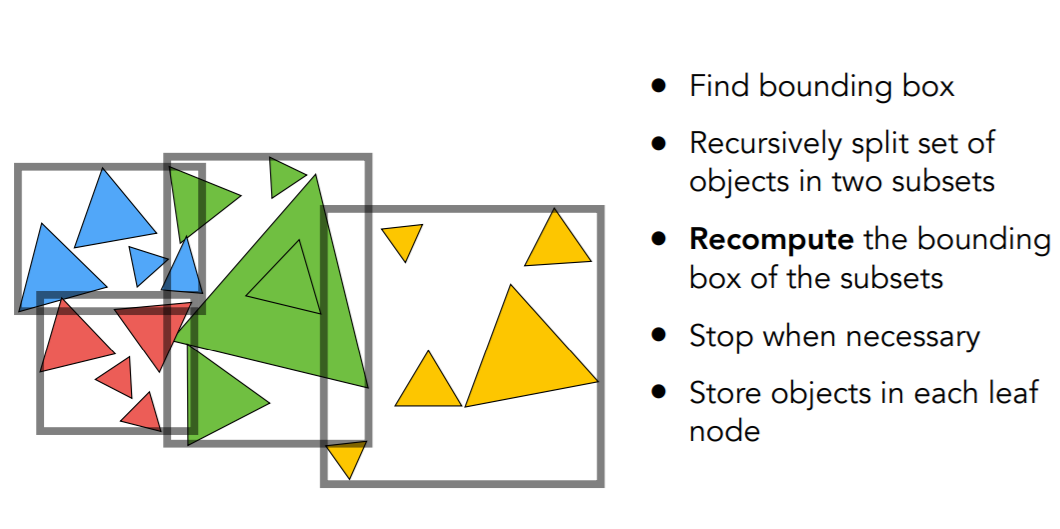
  • 算法
    • 把当前包围盒内的三角形做一个划分
    • 然后把划分得到的两个部分分别求包围盒

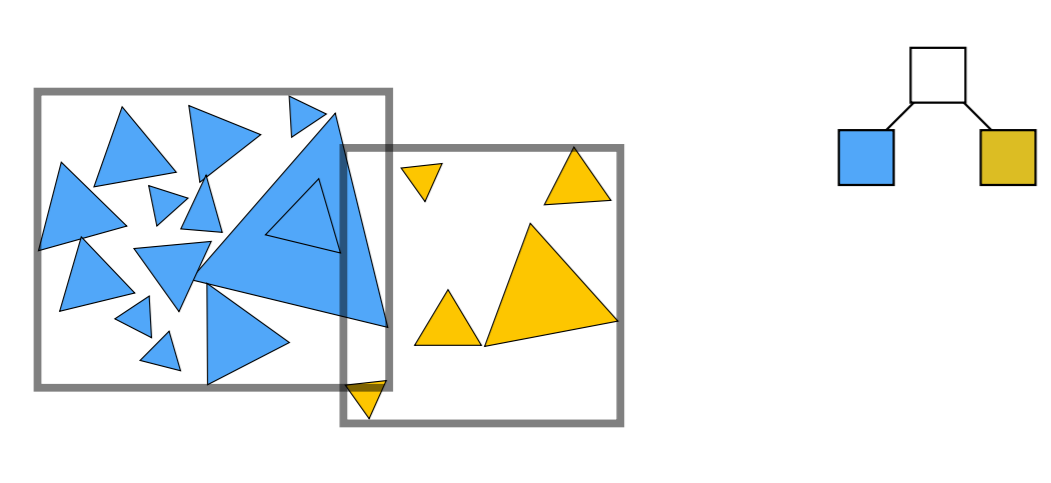
  • 一个物体只可能属于一个叶子结点
  • 不需要求三角形和包围盒的交点
  • 避免了 KD-Tree 的问题
  • 但是 BVH 并没有把整个空间划分开，两个子结点可能有重合部分
    • 一个好的划分，重叠部分尽量小
    • BVH 的研究

  • 怎么选取划分方向
    • 可以学习 KD-Tree，横竖交替划分，尽量均匀
    • 但是可能有一个轴还是很长
      • 所以可以每次选择较长的轴进行划分
    • 可以选取中间的物体进行划分
      • 保证三角形数量差不多
      • 树的深度小，更平衡
        • 涉及排序问题，重心排序
        • 找第 \(k\) 大的数有 \(O(n)\) 的算法
          • 快排思想算法
  • 适合静态场景
    • 动态需要修改
  • BVH 的存储和 KD-Tree 类似
  • 伪代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Intersect(Ray ray, BVH node) {
    if (ray misses node.bbox) {
        return;
    }

    if (node is a leaf node){
        test intersection with all objs;
        return closest intersection;
    }

    hit1 = Intersect(ray, node.child1);
    hit2 = Intersect(ray, node.child2);
    return the closer of hit1, hit2;
}