GAMES101.闫令琪.03.几何(Lecture 10-12)

Posted on Edited on In Views:
Geometry, 基本表示方法, 曲线与曲面, 贝塞尔曲线, 网格处理, 阴影图
  • https://www.bilibili.com/video/av90798049

Lecture 10

  • Geometry (Introduction)
  • 几何（基本表示方法）

现实

  • 曲面
    • 现实生活中，我们不管离得多近，也看到不到小三角形，是真正的曲面
  • 布料，透明现象，摩擦力
    • 纤维（fiber）
    • 股（ply）
    • 线（thread）
    • 布料
  • 水滴
    • 水花飞溅
    • 水的表面张力
  • 城市
    • 内部物体很多，树（树叶），草
    • 怎么存储
    • 怎么渲染这么多物体
      • Big Hero 6 （超能陆战队）
      • 城市远景的渲染，怎么快，怎么优化
  • 动物的毛发
  • 细胞（微观几何）
  • 树，树枝

几何的表示

  • 隐式（Implicit）、显式（Explicit）

隐式表示方法

  • 不告诉你点具体在哪，但是告诉你这些点满足的关系
  • 例如球：\(x^2+y^2+z^2=1\)
  • 一般化的函数：\(f(x,y,z)=0\)

好处

  • 容易判断位置关系
    • 例如判断一个点是否在内部
  • 很难找到所有满足关系的所有点，但是给定一个点后，容易判断是否在它上面

缺点

  • 给你一个表达式，很难看出表达的是什么

\[ f(x,y,z)=(2-\sqrt{x^2+y^2})^2+z^2-1=0 \]

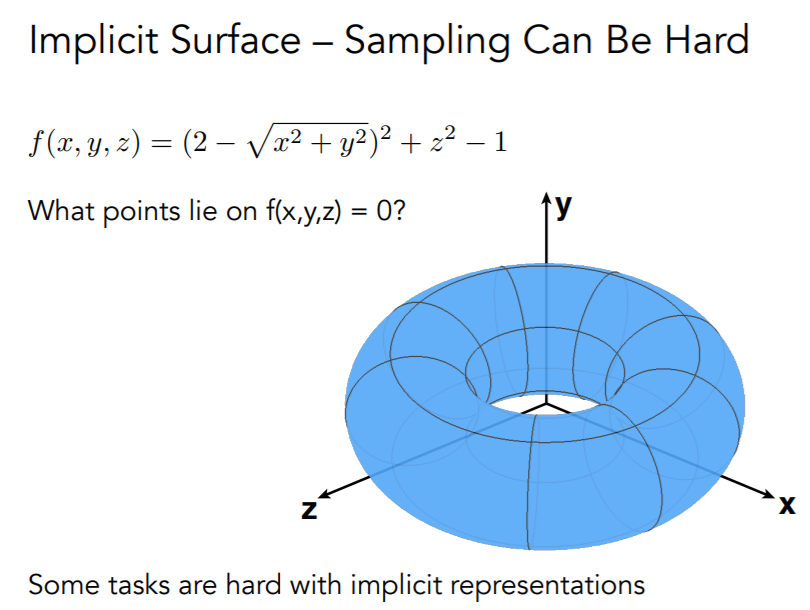
显示的表达方法

  • 直接给出点（given directly）
    • 例如之前给出的三角形面
  • 通过参数映射的方法定义的表面（parameter mapping）
    • 把 \((u,v)\) 全过一遍就找到了结果
    • 类似纹理

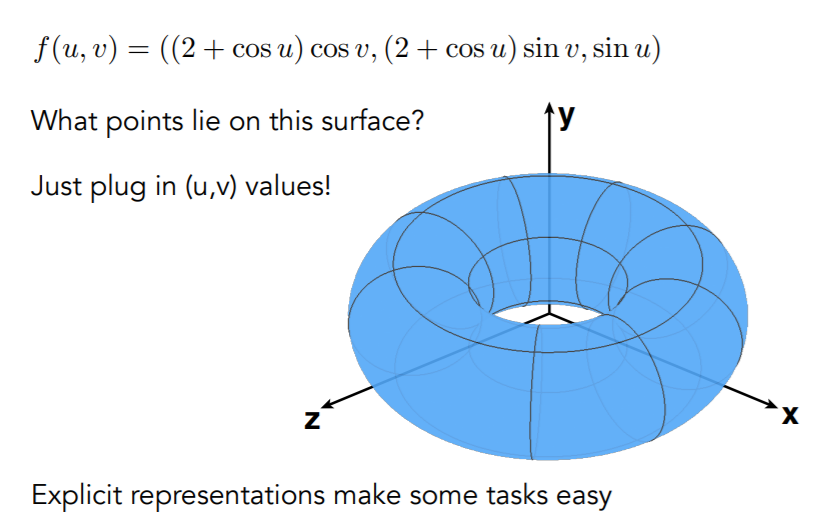
缺点

  • 很难判断一个点是否在内部 /上面

\[ f(u,v)=(\cos u\sin v,\sin u\sin v,\cos v) \]

  • 是一个球面（单位球），但是直接给你一个表达式很难看出，而且不好判断点和几何体的位置关系

隐式表示方法

Algebraic Surfaces (Implicit)

  • 数学公式
  • 如下是一个爱心

\[ (x^2+\dfrac{9y^2}{4}+z^2-1)^3=x^2z^3+\dfrac{9y^2z^3}{80} \]

Constructive Solid Geometry (Implicit)

  • CSD
  • 通过定义几何体之间的集合运算获取新的集合体
  • 布尔运算 Boolean operation

Distance Functions (Implicit)

  • 距离函数
  • SDF：Signed Distance Function
  • 对空间中的每一个点，都求其到物体表面的最短距离（外部为正、内部为负）

  • 对 SDF 进行 blend
  • 一个例子
    • A 到 B 的一个运动状态，阴影表示被遮挡
    • 想通过 A 和 B 得到中间状态（理想：左边一半黑色、右边一半白色）
    • 直接作 blend，变成黑、灰、白各占 \(\dfrac{1}{3}\)
    • 对 SDF 做 blend，与理想一致

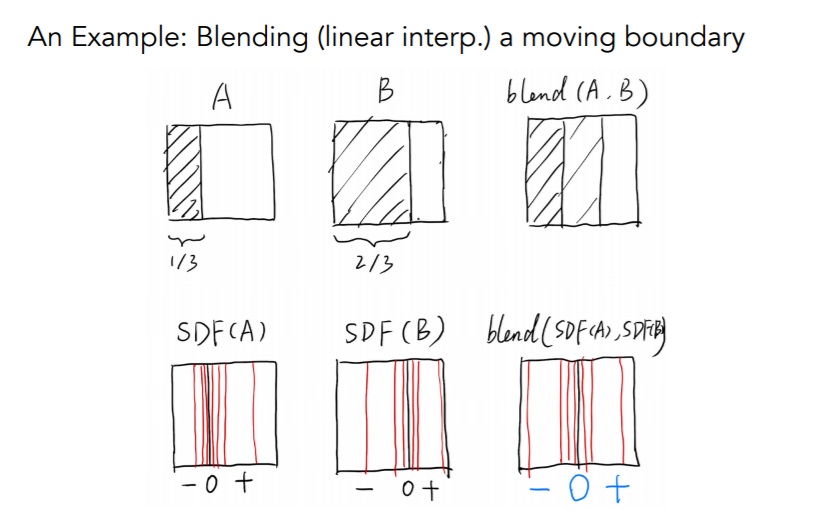
  • 另外一个例子

  • 距离函数很强
  • 怎么从距离函数还原出原来的点
    • 把距离函数为 0 的位置全找出来就得到了表面
  • 距离函数不太好写成解析的形式
    • 水平集方法

Level Set Methods (Also implicit)

  • 水平集方法
  • 也是距离函数，把距离存在网格里，只是表示方式不同
    • 非网格上的点：双线性插值
  • 地理：等高线
  • 三维空间水平集，纹理
  • 医学：CT，MRI
  • Level Sets in Physical Simulatio
    • 水滴滴到水里

Fractals (Implicit)

  • 分形
  • Exhibit self-similarity, detail at all scales
  • 自相似性
    • 渲染的时候会引起强烈的走样

隐式表示方法评价

  • 缺点
    • difficult to model complex shapes
      • 复杂形体难以表示
  • 优点
    • compact description (e.g., a function)
      • 表示简单
    • certain queries easy (inside object, distance to surface)
      • 方便查询（内部、外部）
    • good for ray-to-surface intersection (more later)
      • 容易与光线求交（光线跟踪算法）
    • for simple shapes, exact description / no sampling error
      • 准确描述物体
    • easy to handle changes in topology (e.g., fluid)
      • 容易控制几何变化

Lecture 11

  • Geometry 2 (Curves and Surfaces)
  • 曲线与曲面

显式表示方法

  • triangle meshes
  • Bezier surfaces
  • subdivision surfaces
  • NURBS
  • point clouds

Point Cloud (Explicit)

  • 点云
  • 点表示的够细，就看不出来点与点之间的间隔
  • 精细模型：特别密集的点
  • 三维扫描的输出
  • 点云如何变成（三角形的）面
    • 一个研究问题

Polygon Mesh (Explicit)

  • 多边形面
    • 三角形面、四边形面
  • Perhaps most common representation in graph

文件格式 .obj

  • The Wavefront Object File (.obj) Format
  • Just a text file that specifies vertices, normals, texture coordinates and their connectivities
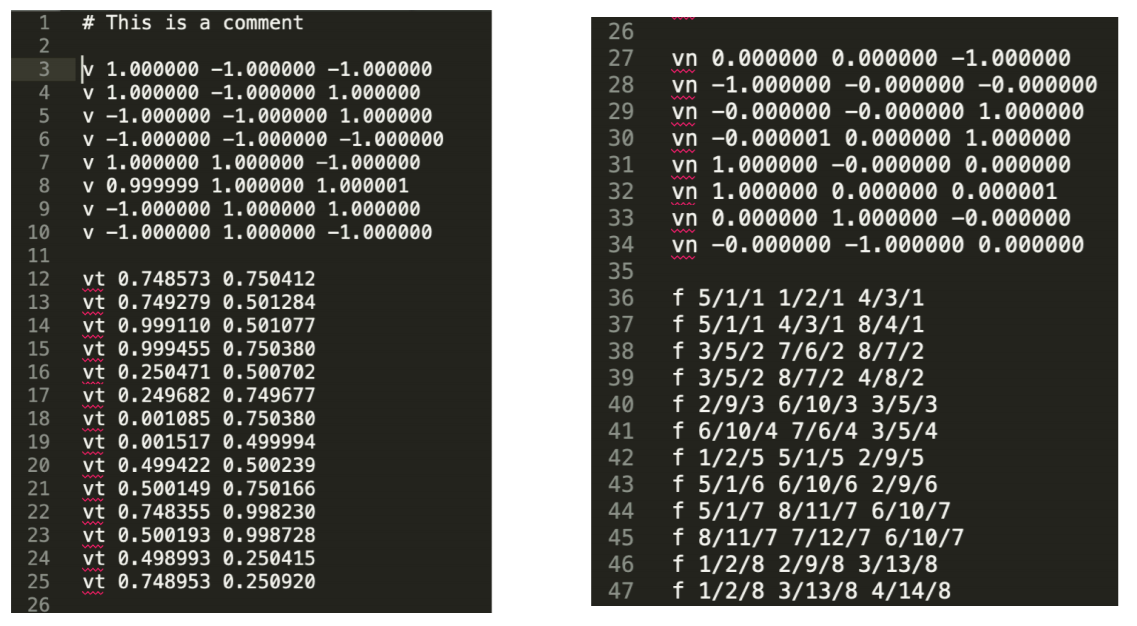
  • 一个立方体的例子
    • 以下数据存在冗余（自动建模产生的）
    • f 表示怎么形成三角形
    • f 5/1/1 1/2/1 4/3/1
    • 三角形的三个顶点（v / vt / vn）
      • 第 5 个顶点（第 1 个纹理坐标、第 1 个法线）
      • 第 1 个顶点（第 2 个纹理坐标、第 1 个法线）
      • 第 4 个顶点（第 3 个纹理坐标、第 1 个法线）

Curves

  • 曲线
  • Camera Path
    • 摄像机沿着某条曲线运动（转换视点方向）
  • 定义字体

Bezier Curves(Explict)

  • 贝塞尔曲线
  • 通过参数定义的，因此是显式的
  • 通过控制点定义曲线（4/3）
    • 控制点：定义切线、起始点、终点

Bézier Curves – de Casteljau Algorithm

  • 通过任意个控制点生成曲线
  • quadratic Bezier（3 个点）

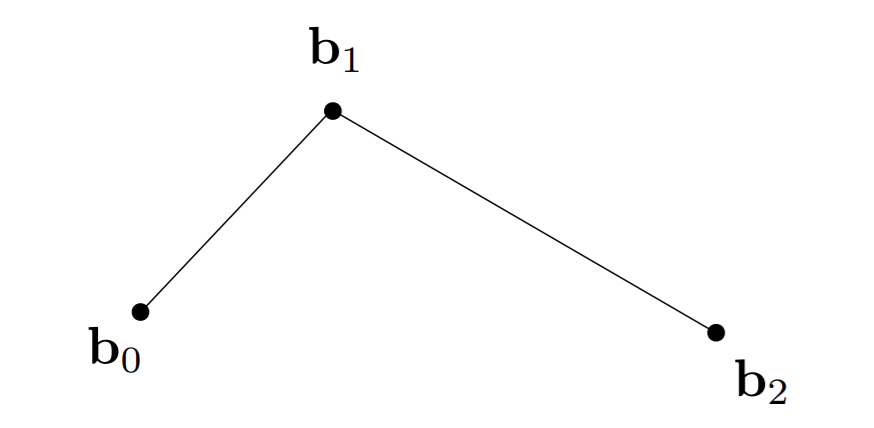
  • \(b_0\) 出发，\(b_2\) 结束，\(b_1\) 控制方向
  • Insert a point using linear interpolation
  • 时间 0 在点 \(b_0\)，时间 \(1\) 在点 \(b_2\)，问时间 t 点在哪里？
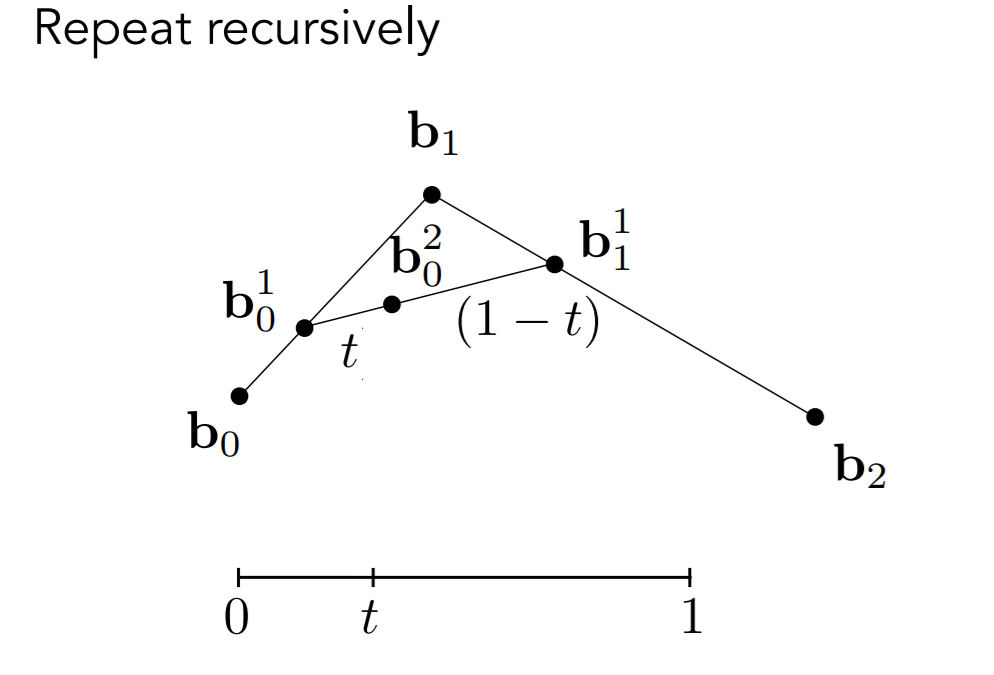
  • 对当前的所有线段进行一个插值，直到无法插值（只有一条线段上的一个点）
    • 每趟插值减少一条线段
  • 例如
    • \(b_0b_1\) 插值出 \(b_0^1\)，\(b_1b_2\) 插值出 \(b_1^1\)
    • 例如 \(b_0^1b_1^1\) 插值出 \(b_0^2\)

Evaluating Bézier Curves Algebraic Formula

  • 代数形式
  • 4 个点

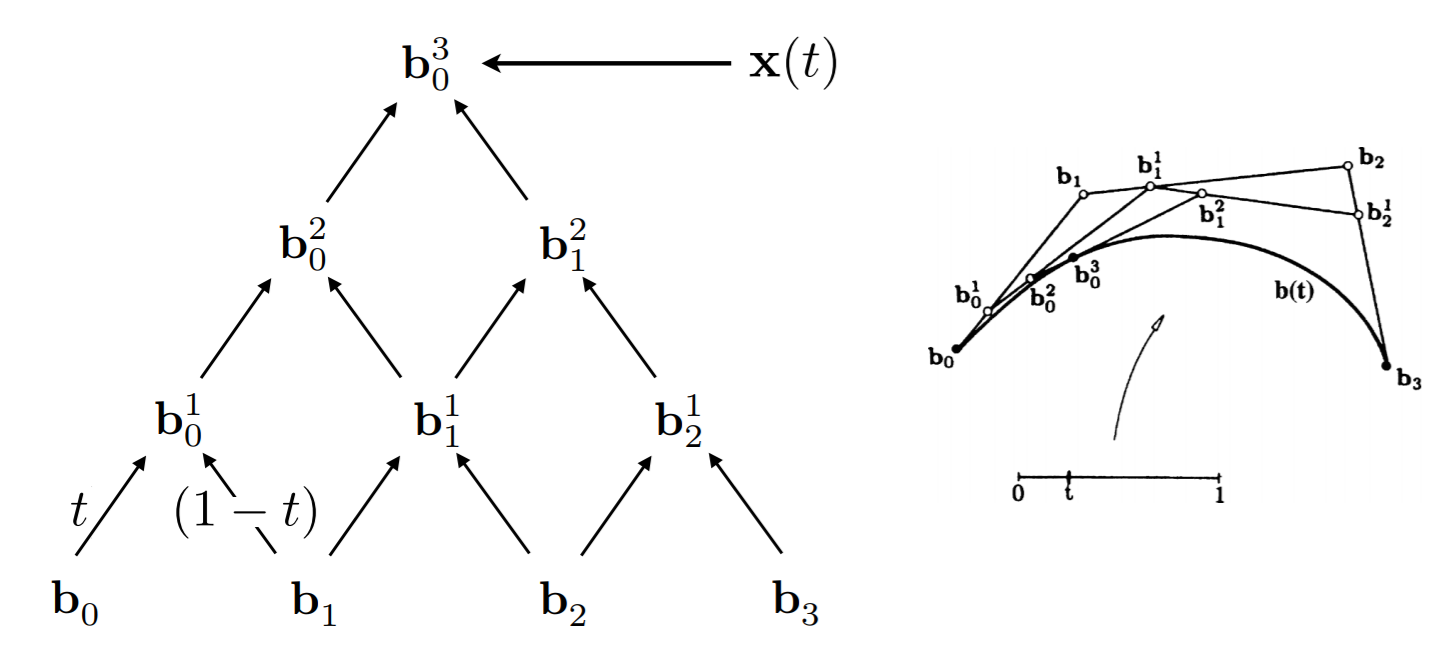
  • 3 个点

\[ \begin{aligned} b_0^2&=tb_0^1+(1-t)b_1^1\\ &=t[tb_0+(1-t)b_1]+(1-t)[tb_1+(1-t)b_2]\\ &=t^2b_0+2t(1-t)b_1+(1-t)^2b_2 \end{aligned} \]

  • 4 个点

\[ b^n(t)=b_0(1-t)^3+b_13t(1-t)^2+b_23t^2(1-t)+b_3t^3 \]

  • 是 1 的二项式展开

\[ b^n(t)=b_0^n=\sum_{j=0}^{n}b_jB_j^n(t) \]

\[ B_j^n(t)=\mathbf{C}_n^it^i(1-t)^{n-i}={n\choose i}t^i(1-t)^{n-i} \]

  • 输入为三维坐标，三维贝塞尔曲线
  • 一些性质（4个控制点情况下）
    • \(b(0)=b_0\)
    • \(b(1)=b_3\)
    • \(b'(0)=3(b_1-b_0)\)
    • \(b'(1)=3(b_3-b_2)\)
  • 控制点做仿射变换后生成的贝塞尔曲线和原来的贝塞尔曲线仿射变换后形成的曲线是一样的
    • 投影变换不行
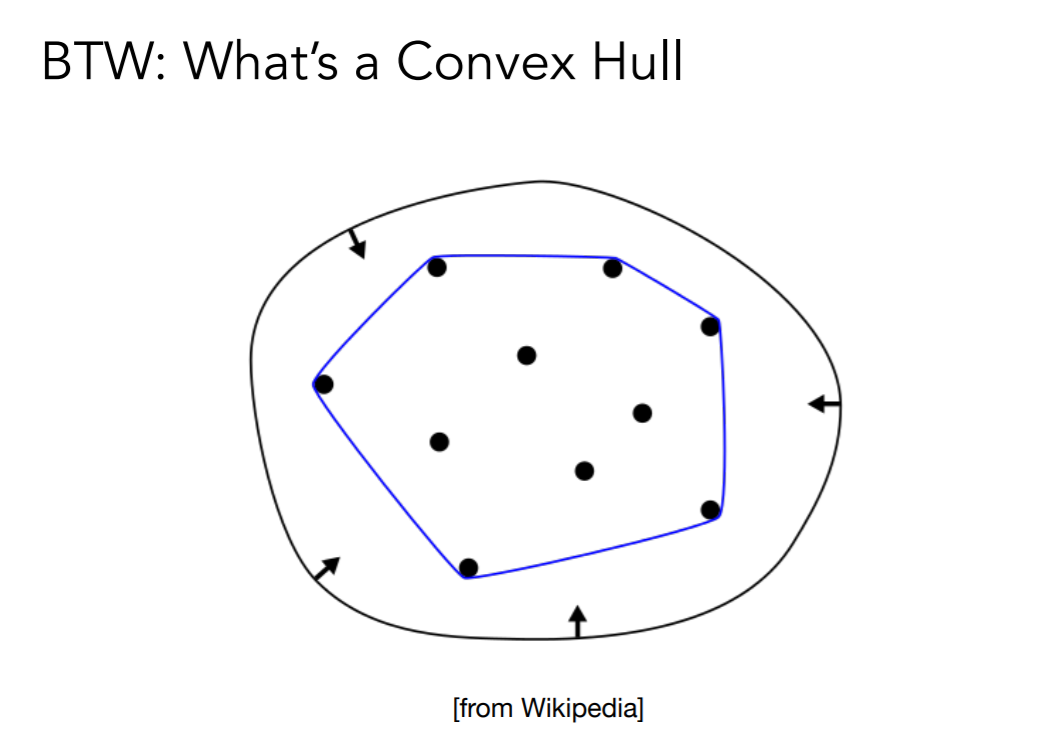
  • 凸包性质
    • 画出来的贝塞尔曲线一定在控制点形成的凸包内

Piecewise Bezier Curves

  • 分段考虑
    • 在线演示：http://math.hws.edu/eck/cs424/notes2013/canvas/bezier.html
  • 控制点多了，不太好控制形成想要的形状

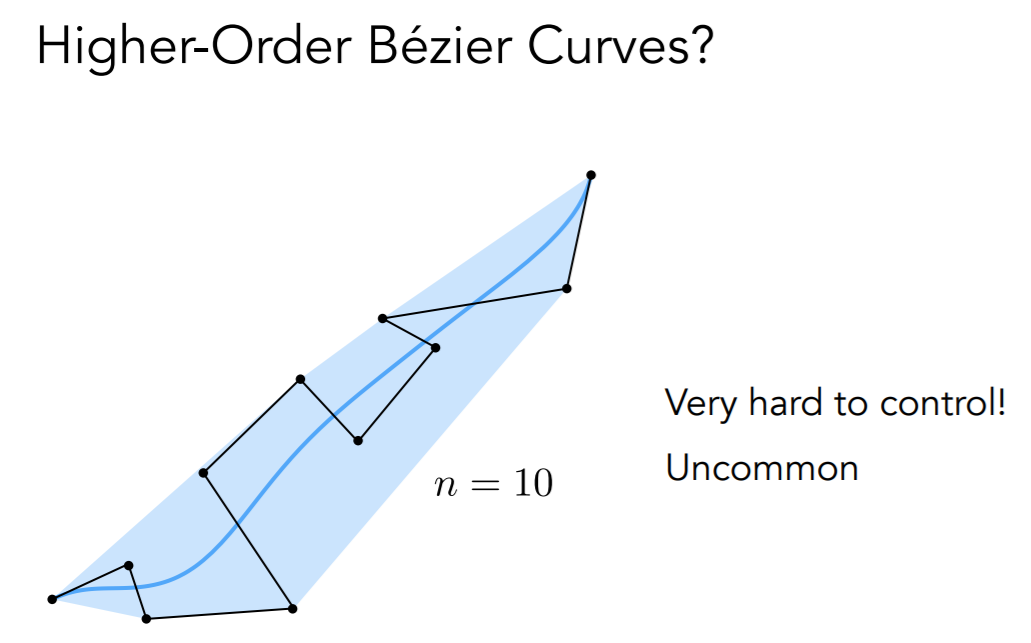
  • 每 4 个控制点定义一个贝塞尔曲线
    • 广泛应用：fonts, paths, Illustrator, Keynote
    • PhotoShop 的钢笔工具
  • 怎么样让连接点光滑？
    • 切线的斜率相同
    • \(3(b_3-b_2)=3(b_4-b_3)\)
    • \(b_2+b_4=2b_3\)
  • \(C^0\) 连续：点是同一个点
  • \(C^1\) 连续：斜率（一阶导数）连续

其他问题

  • 高阶贝塞尔曲线转低阶

Splines 样条

  • a continuous curve constructed so as to pass through a given set of points and have a certain number of continuous derivatives.
  • In short, a curve under control
  • 通过这些点

B-Splines

  • B样条曲线
  • basis splines（基函数样条）
    • 伯恩斯坦多项式作为基函数，进行一个加权平均
  • Require more information than Bezier curves
  • Satisfy all important properties that Bézier curves have (i.e. superset)
  • 提出动机
    • 如果使用贝塞尔曲线，改动一个点，可能会影响整条曲线
      • 分段贝塞尔曲线没有这个问题（边界问题）
    • 然而我们希望只影响局部的曲线

NUBRBS

  • 非均匀有理 B 样条

深入几何内容

  • https://www.bilibili.com/video/av66548502

贝塞尔曲面

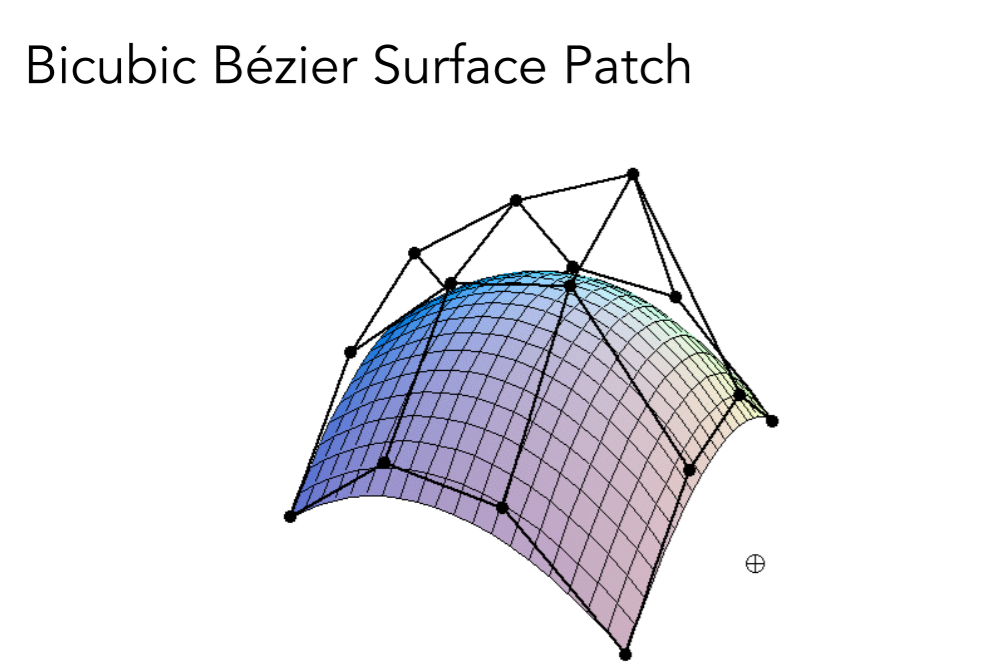
  • 双线性插值的思想
  • 两个方向上做两趟贝塞尔曲线
  • 复杂的问题：贝塞尔曲面的混合

网格计算

  • 网格细分：mesh subdivision

    • upsampling

  • 网格简化：mesh simplification

    • downsampling

  • 网格正则化：mesh regulation

    • 网格正则化
    • 原来的三角形可能有大有小，渲染困难

Lecture 12

  • Geometry (Mesh Operation)

  • 几何（网格处理）

  • 2019 图灵奖：Ed Catmull，Pat Hanrahan

细分 Mesh Subdivision

  • 引入更多三角形
  • 三角形的位置发生点变化，更加光滑

Loop Subdivision

  • Loop：发明这个算法的人叫 Loop
  • 前提假设是原来表示物体的方式i就全都是三角形
  • 三角形分为 4 个

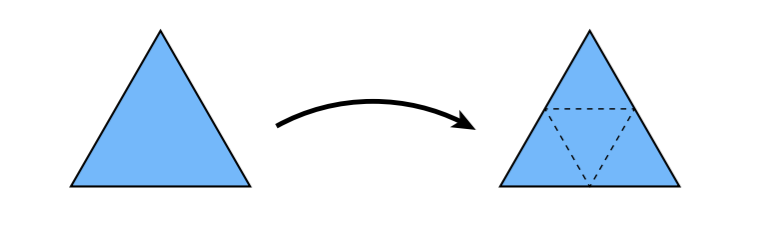
  • 将顶点划分为新/老顶点，使用不同的更新方法去更新
    • 新：边的中间
    • 老：原来存在的
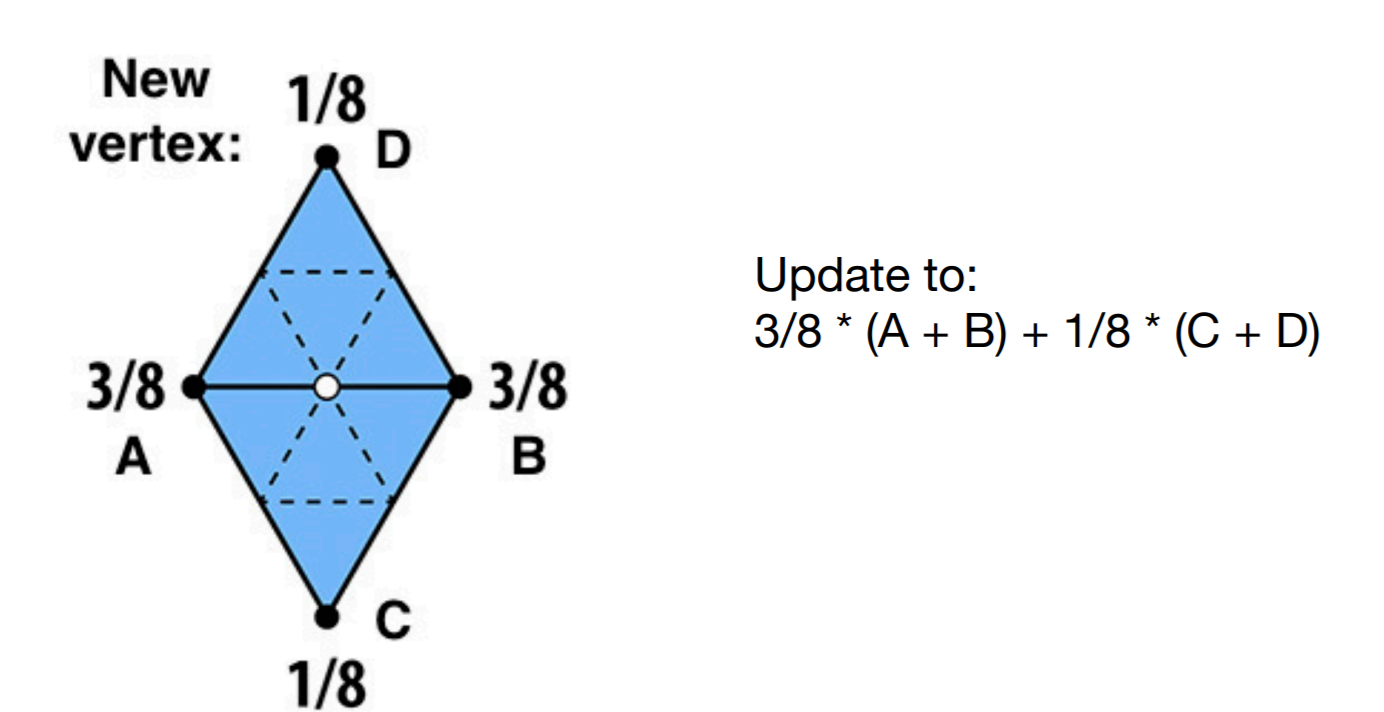
  • 新的顶点的更新方法
    • AB 指更新的点所在的边（被两个三角形共享）
    • CD 指上面个的两个三角形剩下的两个点
    • 直观上的理解：AB 近（贡献大），CD 远（贡献小）

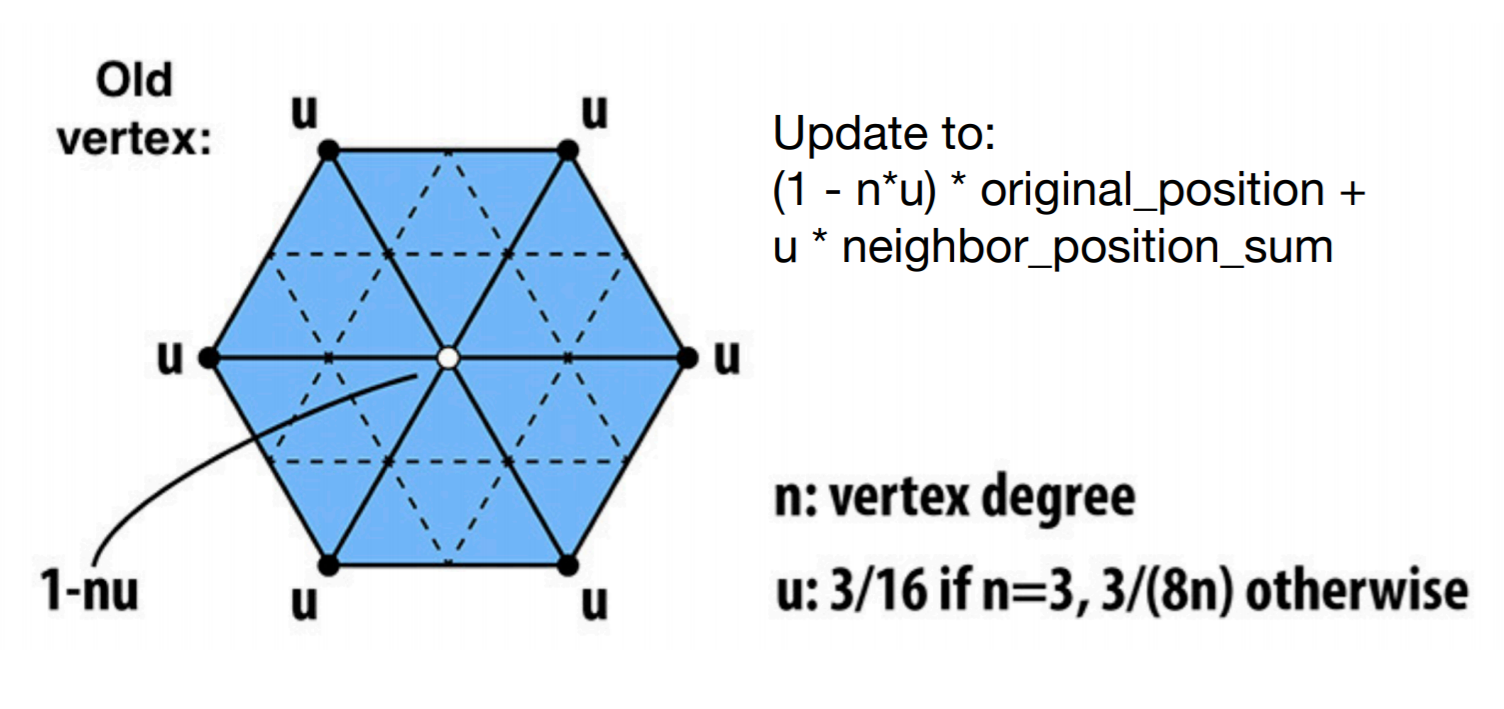
  • 老的顶点的更新方式
    • 老的顶点被若干（\(n\)）个三角形共享，结点度为 \(n\)
    • 考虑周围顶点的影响同时还要考虑自己原来的位置
      • 周围顶点的平均 / 和
      • 自己原来的位置
    • \(u\) ：一个与 \(n\) 相关的数

Catmull-Clark Subdivision

  • 适用于一般的形状表示
  • 一些定义
    • Quad face：四边形面
    • Non-quad face：非四边形面
    • Extraordinary point：奇异点
      • 度不为 4 的点

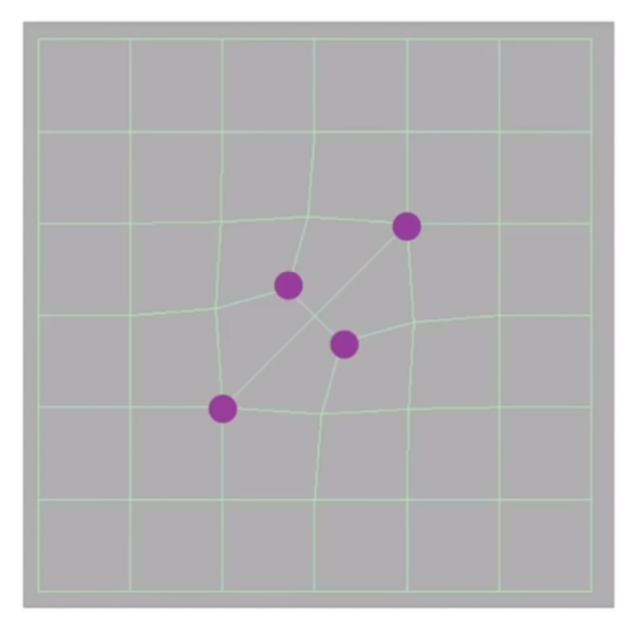
产生新的点

  • 产生算法
    • 对于每个面，我们取所有边的中点以及面上的中点（重心）
    • 将边上的中点和面的中点连起来
  • 经过一次细分之后
    • 奇异点
      • 原来的奇异点还是奇异点
      • 增加的奇异点个数：原来非四边形面的个数
    • 非四边形面
      • 非四边形面全都消失了
    • 每一个非四边形面都会消失，并且引入一个奇异点
  • Catmull-Clark 细分，在第一步操作时会引入 \(n\) 个奇异点，之后的操作不会再引入奇异点
    • \(n\)：初始非四边形面的个数

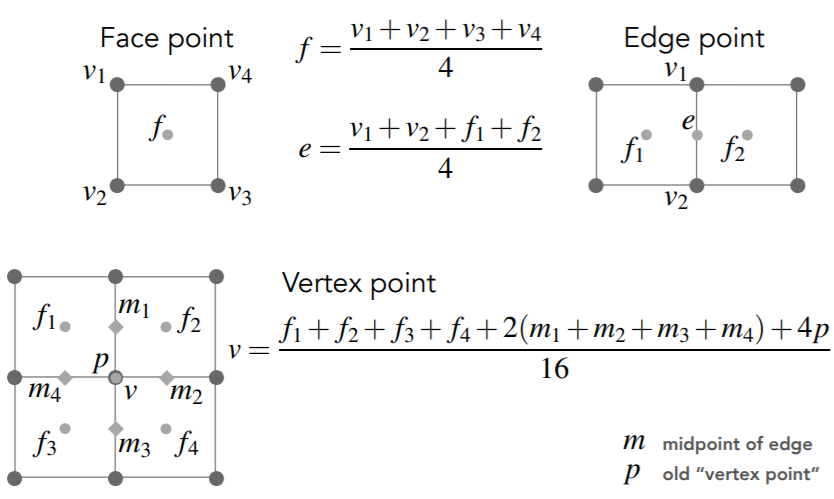
新的点的位置计算

  • 点分为 3 类
    • Face Point：在面的中心的新的点
      • 关联的顶点
    • Edge Point：在边的中心的新的点
      • 关联的边的两个顶点、关联的边关联的面的中心
    • Vertex Point：老的顶点
      • 自己、关联的面的中心、关联的边的中心

  • Geri's Game
    • 最早的一批利用曲面细分做的动画

简化 Mesh Simplification

  • 简化需求的产生
    • 如果一个物体离得很远，没必要划分得很细致
      • 简化后，效果差不多，但是计算量小很多
    • 不同情况下我们会选用不同复杂程度的三角形（几何模型）
  • 几何层次结构的变化、切换很难
    • 例如远处用精细模型，近处用简化模型，但是什么时候切换、怎么平滑切换是个问题
  • 怎么简化
    • 不能直接删除三角形，会有洞
  • 一种方法：边坍缩（Collapsing An Edge）
    • 找到一条边，然后把这条边收缩为一个点

边坍缩

  • 坍缩哪些点？怎么坍缩
    • 二次误差度量
  • 二次误差度量（Quadric Error Metrics）
    • 怎么放置新的点（下图为例）
      • 5 点平均：矮了很多
      • 3 点平均：还是会比轮廓矮
      • 找一个点，满足这个点到原来 4 个面的平方和最小

  • 算法：为每一条边用最小二次误差进行打分，首先坍缩误差最小的边
    • 算法问题
      • 坍缩一条边之后会影响其他边的最小二次误差
      • 需要重新计算被这条边影响的边的最小二次误差
    • 数据结构：堆（优先队列）
    • 算法正确性
      • 贪心算法，并不保证最重的是全局最优解（可能陷入局部最优）
    • 实际效果还不错
      • 图形学本身的特点