GAMES101.闫令琪.02.Shading(Lecture 07-09)
- https://www.bilibili.com/video/av90798049
Lecture 07
- Shading 1 (Illumination, Shading and Graphics Pipeline)
- 着色(光照与基本着色模型)
Lecture 08
- Shading 2 (Shading, pipeline and texture mapping)
- 着色(着色频率、图形管线、纹理映射)
Blinn-Phong 模型
- ambient + diffuse + specular
- 单位向量
- 光源方向:\(\vec{l}\)(指向光源)
- 法向:\(\vec{n}\)
- 视线方向:\(\vec{v}\)
- 光线反射方向:\(\vec{r}\)
- 光源到物体反射点的距离 \(r\)
(1) Diffuse
\[ L_d=k_d\dfrac{I}{r^2}\max(\vec{n}\cdot\vec{l},0) \]
(2) Specular
- 半程向量:\(h\)
\[ \vec{h}=bisector(\vec{v},\vec{l})=\dfrac{\vec{v}+\vec{n}}{||\vec{v}+\vec{n}||} \]
\[ L_s=k_s\dfrac{I}{r^2}\max(\vec{n}\cdot\vec{h},0)^p \]
- Phong 模型中使用 \(\vec{r}\cdot\vec{v}\)
- Blinn-Phong 模型是一个改进
- 相对好算
- \(\vec{v},\vec{r}\)
的夹角大于90度时应该也能有部分高光
- 不会出现 Phong 模型中的高光断层问题
- Blinn-Phong 模型是一个改进
- \(p\) 限制反光范围
- 实际应用:100 - 200
(3) Ambient
- 模拟间接光照
- 实际上是不存在的 FAKE
\[ L_a=k_aI_a \]
- 光源到物体的距离会引发能量损失,视点到物体的距离不会
Shading Frequencies
- 着色频率:多大的区域应用一次着色算法
- 频率越高,着色算法应用的区域越小,着色算法使用的次数越多
- Flat Shading
- 逐三角形 Face
- 一个三角形只有一个法线,三角形内部没有颜色变化
- Gouraud Shading
- 逐顶点 Vertex
- 一个三角形的每一个顶点进行一次着色计算,内部颜色使用插值计算出来
- Phong Shading
- 逐像素 Pixel
- 对三角形所在区域的每一个像素进行光照计算
- 模型足够复杂(面的细分够小)的时候,可能面的个数比像素多
- 逐三角形绘制可能耗时
- 逐像素绘制也不一定比逐三角形绘制效果好
怎么知道顶点/像素的法线
- 如果知道已知模型,可以通过已知的几何模型中获取(例如本身是球体)
- 不知道的话,可以对这个顶点关联的面的法线求一个平均
- 亦可以加权平均
- 像素的法线:插值
- 重心坐标
Graphics Pipeline(Real-time Pipeline)
- vertex processing
- triangle processing
- rasterization
- fragment processing
- framebuffer processing
Shader
- vertex shader
- fragment shader
- OpenGL: GLSL
Texture Mapping
- 纹理映射
- 纹理用于定义着色的时候所用的属性
- 一般用于代替漫反射系数 \(K_d\)
- 3D 物体表面可以和一张 2D 表面相对应
- 空间中的三角形怎么和 2D 平面上的纹理相对应
- 美工设计
- 自动化:parametric(参数化)
- 纹理坐标系 uv
- 通常认为 u,v 范围都是 [0, 1]
- 纹理可以被重复使用
- 设计的好的时候,重复的时候可以无缝连接
- 纹素:texel
- a pixel on a texture
Lecture 09
- Texture Mapping
- 插值、高级纹理映射
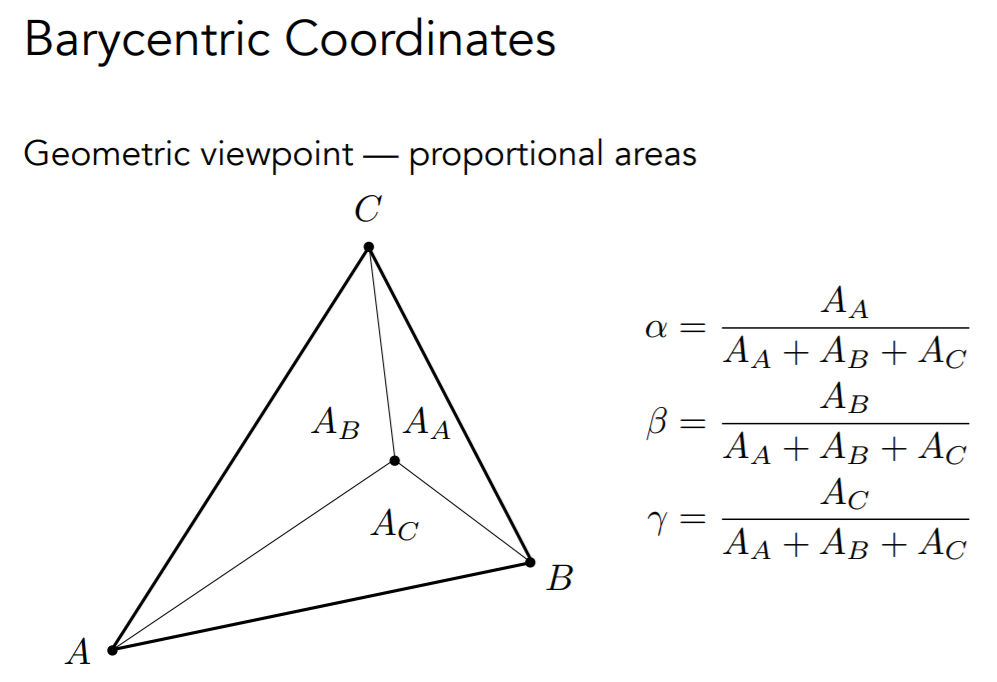
Barycentric Coordinates
- 重心坐标
- 为了做三角形内的插值
- 知道顶点属性,可以平滑的插值三角形内部的属性
- 三角形 \(ABC\) 所在平面内的任意一点 \((x,y)\) 都可以用 \(ABC\) 三个顶点的坐标线性组合得出
\[ (x,y)=\alpha A + \beta B+\gamma C,\alpha+\beta+\gamma=1 \]
- 如果点 \((x,y)\)
在三角形内部,系数不为负
- 系数与面积相关
- 或者直接利用坐标计算
\[ \begin{aligned} \alpha &=\frac{-\left(x-x_{B}\right)\left(y_{C}-y_{B}\right)+\left(y-y_{B}\right)\left(x_{C}-x_{B}\right)}{-\left(x_{A}-x_{B}\right)\left(y_{C}-y_{B}\right)+\left(y_{A}-y_{B}\right)\left(x_{C}-x_{B}\right)} \\ \beta &=\frac{-\left(x-x_{C}\right)\left(y_{A}-y_{C}\right)+\left(y-y_{C}\right)\left(x_{A}-x_{C}\right)}{-\left(x_{B}-x_{C}\right)\left(y_{A}-y_{C}\right)+\left(y_{B}-y_{C}\right)\left(x_{A}-x_{C}\right)} \\ \gamma &=1-\alpha-\beta \end{aligned} \]
- 可以直接利用重心坐标进行属性插值
- 存在的一个问题,投影变换下重心坐标会变化
- 例如深度值的插值应该在世界坐标系/观察中进行,不能在投影坐标系下进行
Texture Mapping
Simple Texture Mapping
- 插值出 \((u,v)\)
- 然后再在纹理中采样
纹理放大
- Texture Magnification
(1) 纹理太小了怎么办
- 纹理分辨率太低
- 计算出非整数值:插值(Nearest、Bilinear、Bicubic)
- 双线性插值:Bilinear
- 使用临近的 4 个点进行双线性插值
- 两趟线性插值 lerp
- 双三次插值:Bicubic
- 取邻近得到 16 个点进行插值
- 两趟 cubic 插值方法
- 运算量大,但是效果更好
- trade off
(2) 纹理太大了怎么办
- 更严重的问题
- 远处摩尔纹,近处锯齿
- 远处占据了一块很大区域的纹理,简单的取中心点所在的坐标会出问题
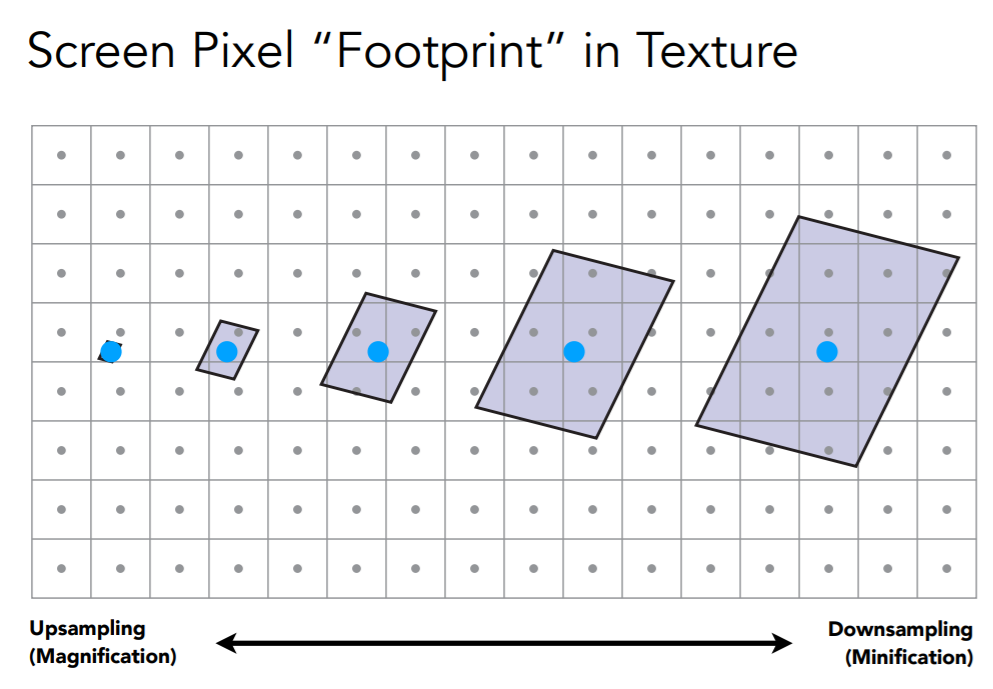
- 超采样,可以解决,但是计算量很大
- 不做采样,立刻知道的话就不会有问题
- Mipmap
- 经典问题:Point Query & Range Query
MipMap
- 允许范围查询
- 正方形、近似的、快
- 通过一张图,生成一系列分辨率的纹理图
- 原始分辨率 64x64
- 生成的一系列的纹理分辨率:64x64, 32x32, 16x16, 8x8, 4x4, 2x2, 1x1
- Level 0 - 6
- 存储量变为原来的 \(\dfrac{4}{3}\)
- 怎么知道需要查询的是哪一张(层次)纹理
- 计算出来
- 取最大值,相当于用一个正方形近似
- \(D=\log_2L\),很巧妙
- 和上面生成纹理分辨率对比
- L = 1 刚好是 Level 0(原始图像)
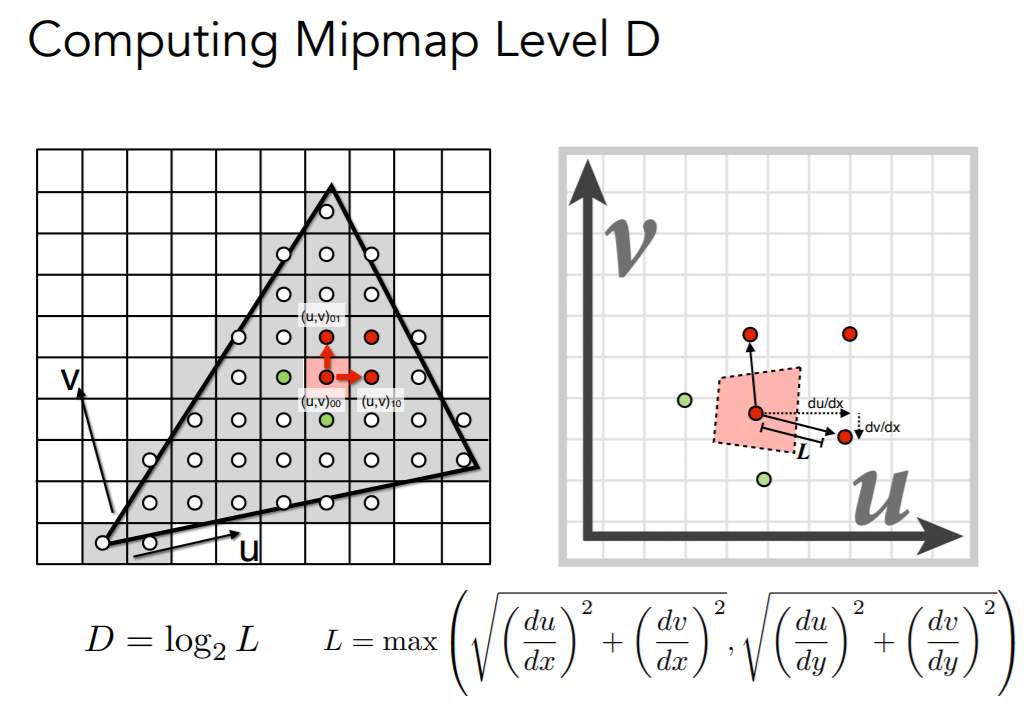
- 由于层是离散的,因此计算出来的层数是不连续的
- 利用三线性插值(Trilinear)计算
- 例如计算出来是 1.6 层,则在第 1 层和第 2 层上分别取最近的 4 个点进行一次双线性插值,然后在层与层之间进行一次线性插值
- MipMap 的问题
- 远处的细节全都被模糊掉了(和超采样相比)
- 三线性插值的近似
- 只能查询正方形,对长条形的区域可能会产生 Overblur
- 一个解决方法:各向异性过滤 Anisotropic Filtering
- 远处的细节全都被模糊掉了(和超采样相比)
各向异性过滤 Anisotropic Filtering
- 水平竖直缩小的倍数不一样,使用矩形去近似
- 部分解决问题,对于横平竖直的矩形查询相对更加准确
- 但是一些斜着的区域还是存在 Over Blur 的问题
- 存储开销变为原来的 4 倍
- RipMap

- 2x 指的是每个方向只压缩 1 次,左上角 4 张图
- 3x:左上角 9 张图(最小的压缩了两次)
- nx:最终收敛到 4 倍存储开销
EWA Filtering
- 不规则的图形利用圆形去近似
- 多次查询,覆盖这个不规则图形(耗时长)
纹理的应用
- In modern GPUs, texture = memory + range query
(filtering)
- 把纹理理解为一块数据,而不仅仅局限在图像上
- Store microgeometry
- Procedural textures
- Solid modeling
- Volume rendering
Environment lighting
- 环境光照
- Environment Map 环境贴图
- 认为光源无限远,没有深度意义,因此可以通过方向采样(不定义位置)
Spherical Environment Map
- 球面光贴图
- 将整个环境光记录在球面上
- 展开到长方形平面上,极点部分会有扭曲的问题

Cube Map
- 解决扭曲问题而提出的
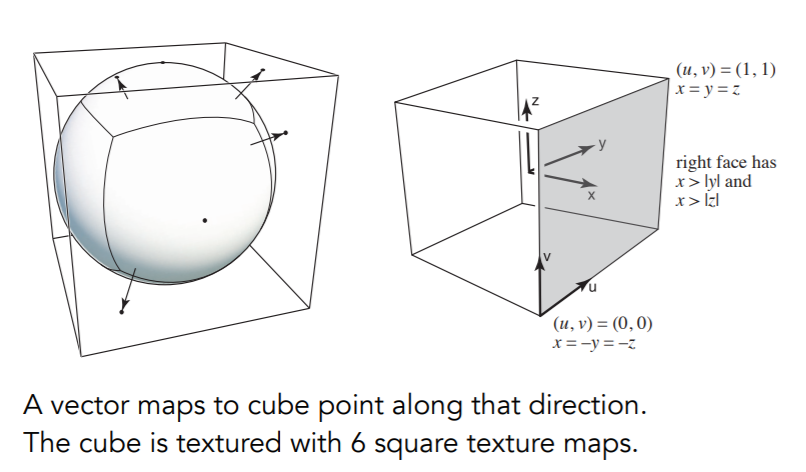
- 产生的问题
- 球面采样更快,立方体需要先判断在哪一个面上

凹凸贴图
- 凹凸贴图(法线贴图)
- Bump Mapping / Normal Mapping
- 复杂的效果,粗糙效果
- 物体的几何信息没有改变,加入一个随机扰动(perturb)
- 常数用于表示凹凸贴图的影响程度

- 蓝色的线是凹凸贴图定义的高度,重新计算法线
- 先算切线,再算法线
- 3 维空间类似
- 原来的法线 \(n(p)=(0,0,1)\)
- \(\dfrac{dp}{du}=c1\ast[h(u+1)-h(u)]\)
- \(\dfrac{dp}{dv}=c2\ast[h(\mathbf{v}+1)-h(\mathbf{v})]\)
- 扰动后的法线(未归一化)\(n=(-\dfrac{dp}{du},-\dfrac{dp}{dv},1)\)
- 可以通过旋转矩阵推导,或者空间想象
- 局部坐标系:切线空间 TBN
位移贴图
- Displacement Map
- 直接把顶点的位置移动了,而不是说简单的影响法线
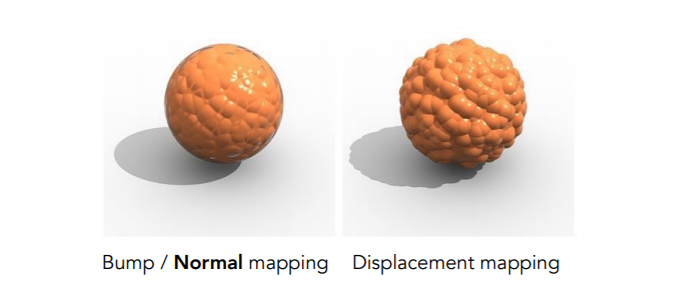
- 和凹凸贴图的区别
- 边缘
- 自己的阴影在自己上面
- 影子
- 要求三角形足够细
- 如果三角形比较大,纹理定义的变换在三角形内部体现不出来
- 要求三角形定义的间隔比纹理间隔更下(频率更高)
- DirextX:动态曲面细分
- 根据需要做细分,而不是所有的三角形都这么细致
3D Procedural Noise + Solid Model
- 程序纹理
- 定义三维空间的噪声函数
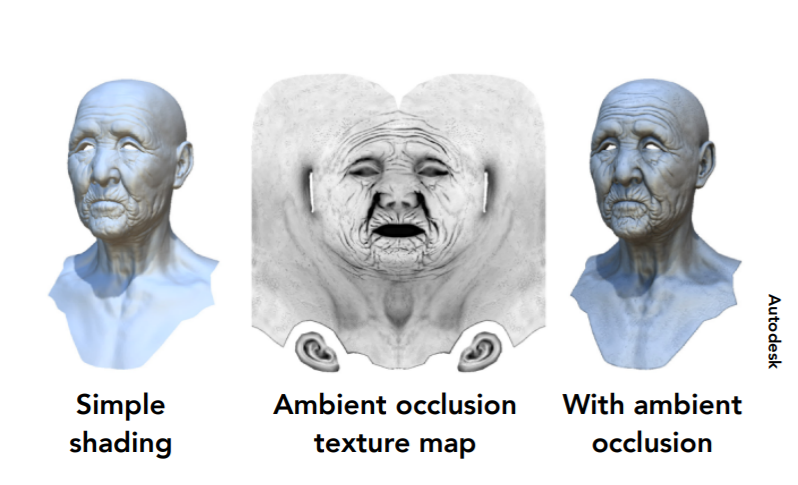
Provide Precomputed Shading
- 记录一些已经计算好的信息
- OpenGL 帧缓冲
- 环境光遮蔽例子
3D Textures and Volume Rendering
- 体渲染
- 例如核磁共振分层扫描,返回了三维信息,把这些记录的信息当作纹理传入用于渲染