GAMES101.闫令琪.01.Lecture(01-06)

Posted on Edited on In Views:
几何变换、光栅化、可见性、阴影
  • https://www.bilibili.com/video/av90798049

Lecture 01

  • Overview of Computer Graphics
  • 计算机图形学概述

Lecture 02

  • Review of Linear Algebra
  • 向量与线性代数

Lecture 03

  • Transformation
  • 变换（二维与三维）

基本变换

  • scale、rotate、shear、reflection
    • 放缩、旋转、错切、对称
  • translate
    • 平移
  • 变换顺序很重要

齐次坐标

  • 统一表示所有变换

Lecture 04

  • Transform Cont.
  • 变换（模型、视图、投影）

欧拉角

  • 表示任意旋转

\[ R_{xyz}(\alpha,\beta,\gamma)=R_x(\alpha)R_y(\beta)R_(\gamma) \]

  • roll, pitch, yaw

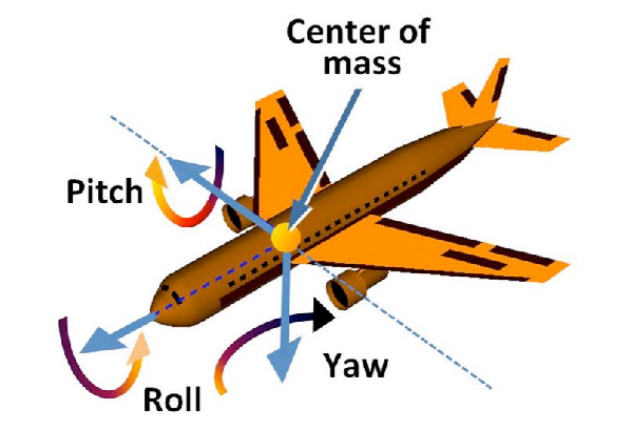
  • 存在万向锁问题

绕任意轴的旋转

  • Rodrigues’ Rotation Formula
  • 推导
  • 绕过原点的单位轴 \(\mathbf{n}\) 逆时针旋转 \(\alpha\) 角度

\[ \mathbf{R}(\mathbf{n}, \alpha)=\cos (\alpha) \mathbf{I}+(1-\cos (\alpha)) \mathbf{n} \mathbf{n}^{T}+\sin (\alpha)\left(\begin{array}{ccc} 0 & -n_{z} & n_{y} \\ n_{z} & 0 & -n_{x} \\ -n_{y} & n_{x} & 0 \end{array}\right) \]

MVP 变换

  • model、view、projection

camera 相机

  • Position
    • \(\vec{e}\)
  • Look-at / gaze direction
    • \(\vec{g}\)
  • Up direction
    • \(\vec{t}\)

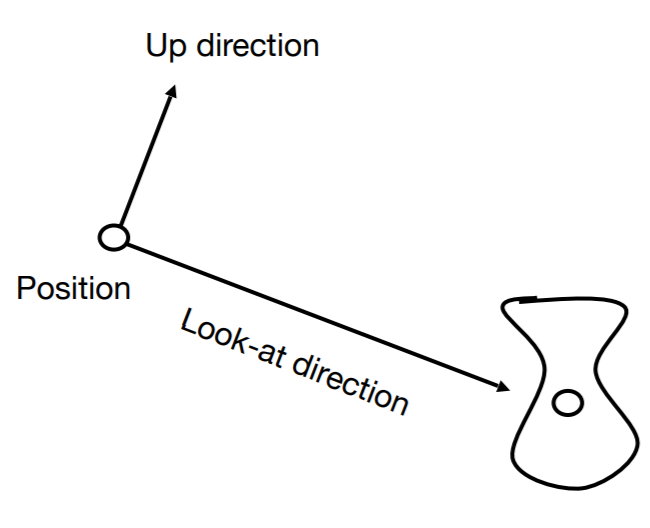
  • 通常变换的结果
    • Position
      • 原点
    • Look-at / gaze direction
      • \(-z\)
    • Up direction
      • \(y\)
  • 变换的过程
    • 位置移动到原点
      • \(-\mathbf{Position_{camera}}\)
    • 旋转（正交变换）

投影变换

  • Perspective projection 透视投影
  • Orthographic projection 正交投影

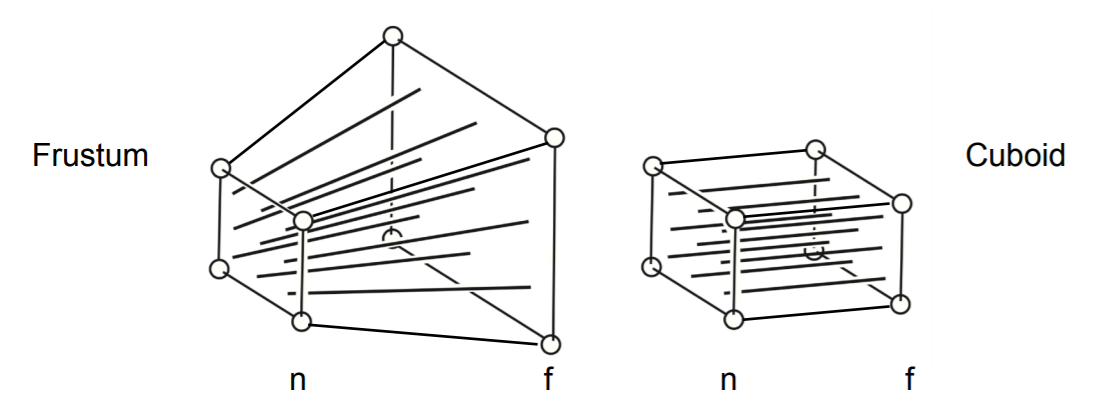
  • 透视变换：变换到 \([-1,+1]^3\)
    • Frustum 转变为 Cuboid（近裁剪面一样大）
    • 平移、放缩

\[ M_{persp} = M_{ortho}M_{persp\to ortho} = M_{scale}M_{translate}M_{persp\to ortho} \]

\[ M_{persp\to ortho}= \begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & -nf\\ 0 & 0 & 1 & 0\\ \end{bmatrix} \]

\[ M_{scale}= \begin{bmatrix} \dfrac{2}{r-l} & 0 & 0 & 0\\ 0 & \dfrac{2}{t-b} & 0 & 0\\ 0 & 0 & \dfrac{2}{n-f} & 0\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]

\[ M_{translate} \begin{bmatrix} 1 & 0 & 0 & -\dfrac{r+l}{2}\\ 0 & 1 & 0 & -\dfrac{t+b}{2}\\ 0 & 0 & 1 & -\dfrac{n+f}{2}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]

\[ M_{ortho}= \begin{bmatrix} \dfrac{2}{r-l} & 0 & 0 & -\dfrac{r+l}{r-l}\\ 0 & \dfrac{2}{t-b} & 0 & -\dfrac{t+b}{t-b}\\ 0 & 0 & \dfrac{2}{n-f} & -\dfrac{n+f}{n-f}\\ 0 & 0 & 0 & 1\\ \end{bmatrix} \]

计算出参数

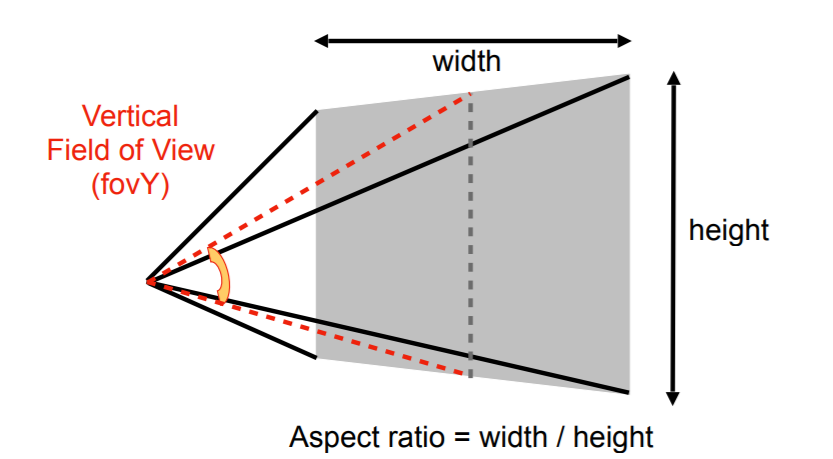
  • Vertical Field-of-View (fovY)
    • 一个角度值
  • Aspect ratio
    • width / height
  • 通过 \(n,f,fovY,aspect\) 计算出 \(l,r,b,t\)
    • \(t=|n|\times\tan\dfrac{fovY}{2}\)
    • \(r=t\times aspect\)

Lecture 05

  • Rasterization 1 (Triangles)
  • 光栅化（三角形的离散化）

光栅化

  • 直接采样
    • 实际上采样点的坐标应该是 \((x+0.5,y+0.5)\)
    • 中心在三角形内，就设置为三角形的颜色
      • 边缘出现走样的问题
  • 怎么判断在三角形内部：叉乘
  • 点 P 在三角形 ABC 内部，以下三个结果同号

\[ \vec{AP}\times\vec{AB},\vec{BP}\times\vec{BC},\vec{CP}\times\vec{CA} \]

  • 点同时在 3 个向量 \(\vec{AB},\vec{BC},\vec{CA}\) 的左边 / 右边

光栅化加速优化

  • 基于三角形覆盖的区域较小

包围盒技术

  • 不需要对所有的点进行判断，只需要对包围盒内的点进行判断
  • AABB 包围盒
    • Axis-Aligned Bounding Box
    • 横平竖直

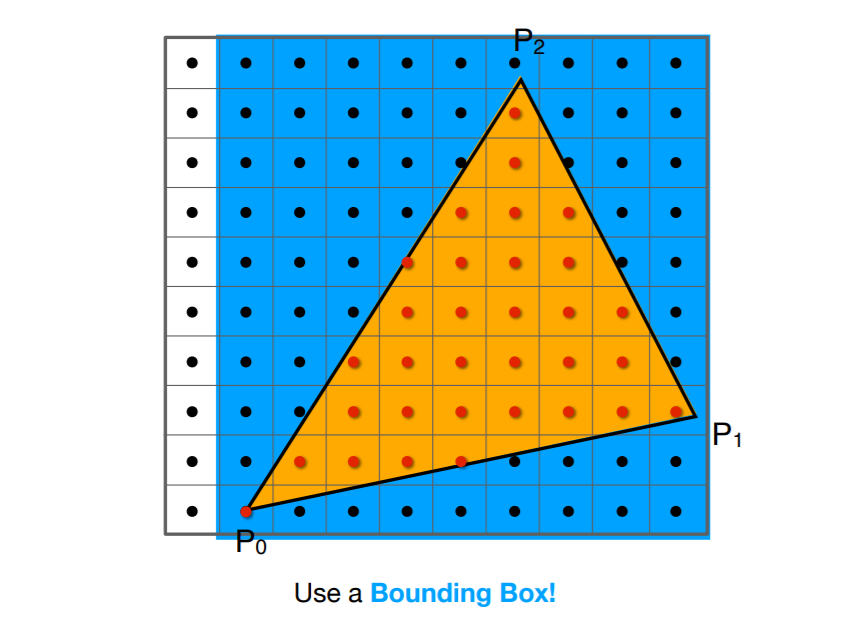
  • AABB 包围盒技术失效
    • 包围盒大，但是三角形小
    • 三角形斜着放
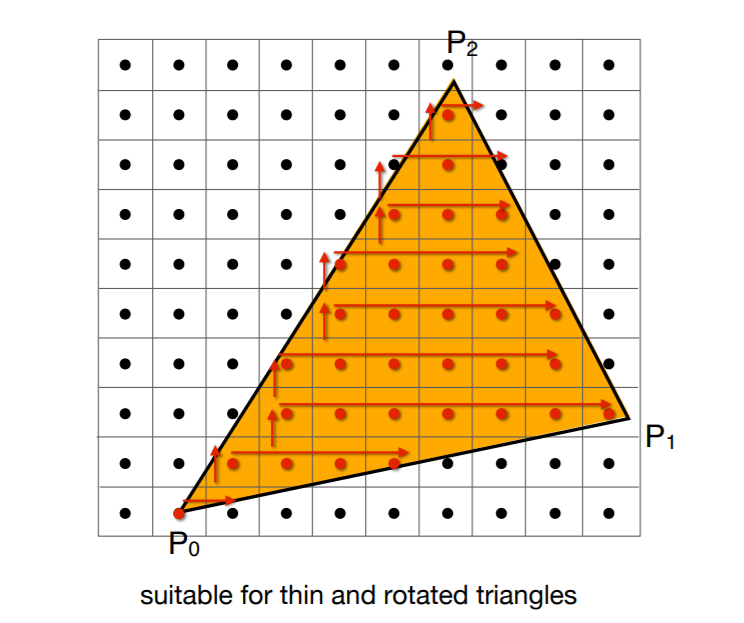
  • 如下方法可以解决 AABB 失效的问题
    • 适合瘦小、斜置的三角形

光栅化显示技术

  • 隔行扫描
    • 每帧只渲染一半
    • 快、看不出来
  • 像素
    • 我们认为是不可分的
    • 实际上在显示设备上可能是由更小的像素（条/点）组成的

  • bayer pattern（iPhone 6S）
    • 像素内分布方式
  • 像素内绿色多，密度大，红蓝差不多
    • 人眼对绿色敏感
  • 屏幕：加色系统（初始黑，全加白）
  • 打印机：减色系统（初始白，全加黑）

Lecture 06

  • Rasterization 2 (Antialiasing and Z-Buffering)
  • 光栅化（深度测试与抗锯齿）

采样问题

  • Sampling Artifacts in Computer Graphics
    • 看上去不太对的东西，瑕疵
    • Errors / Mistakes / Inaccuracies
  • 锯齿 Jaggies
  • 摩尔纹 Moire
    • 奇数行、奇数列去掉，变成小的图，但是显示仍然是和原来一样大
    • 手机拍显示器的屏幕产生的摩尔纹
  • Wagon Wheel Illusion (False Motion)
    • 高速行驶的汽车倒转
    • 人眼在时间中的采样跟不上运动速度

信号与系统的观点

  • 原始图像的频率过高，采样频率跟不上，导致原始的图像不能恢复
  • 采样定理
    • 当采样频率大于信号中最高频率的2倍时，采样之后的数字信号完整地保留了原始信号中的信息
    • 采样过慢，频域上有混叠
  • 反走样的方法
    • 提高采样频率
    • 降低原始图像的频率
      • 采样之前先做模糊化
  • 反走样方法：采样之前先做模糊化
    • 先模糊，后采样 OK
    • 先采样，后模糊 NO
  • 模糊
    • 频域相乘 \(\Leftrightarrow\) 时域卷积
  • 傅里叶变换到频域上可视化
    • 中间水平竖直线，信号强
    • 原因是我们分析图片的时候，会将其看成是重复的（一张一张放一起），边界部分极其高频

Anti Aliasing

  • MSAA 增大了计算量
    • 使用更多的点去判断是否在三角形内
    • 最后通过在三角形内部的采样点的比例计算出近似的覆盖率
  • MSAA 解决的是对信号的模糊操作，得到近似的覆盖率（不是增加分辨率）
    • 有点的复用
    • 例如打开 2x2 的 MSAA 之后，帧率不会变为原来的 \(\dfrac{1}{4}\)
  • 工业界近似采样率的得到，不同的 pattern，点的复用，提高效率
    • MSAA 是 2x2 的正方形 pattern
  • FXAA
    • Fast Approximate AA
    • 先得到有锯齿的图片，然后做后期处理去除锯齿（图像匹配等方法）
    • 和采样无关，是在图形层面上的抗锯齿
  • TAA
    • Temporal AA
    • 时间，复用上一帧的感知，把 MSAA 的采样点分布到不同帧
  • Super resolution / super sampling 超分辨率
    • From low resolution to high resolution
    • Essentially still "not enough samples" problem
    • DLSS (Deep Learning Super Sampling)

可见性

  • 画家算法：先排序，再绘制
  • 问题：互相遮挡

Z-Buffer

  • Depth Buffer
  • 深度缓存
  • 复杂度：\(O(n)\)
    • 指绘制 n 个三角形，每个三角形只覆盖常数个像素
  • 如果配合 MSAA，则应该是每个采样点对应一个深度，而不是每个像素

阴影

Shadow Mapping 算法

  • 光栅化比较难处理全局现象
  • 图像空间的做法
  • 有走样现象
  • 思想：如果点不在阴影里，光源可以看到这个点
  • 经典的 shadow mapping 算法只能处理 点光源/平行光 的阴影
    • 硬阴影
    • 非 0 即 1 的问题
  • 算法
    • 变换到以光源为视点的观察坐标系中，记录深度图
    • 正常渲染到以视点为观察坐标系中，将你看到的点转换到上一步的坐标系中，利用深度值怕段是否在阴影中（能否被光源看到）
  • 一些问题
    • 浮点数判断相等困难，因此会出现黑白条纹的问题
      • shadow map 分辨率问题
        • 一般游戏中选择阴影质量，就是修改分辨率
      • 记录值的精度问题
    • 加入一个 bias
    • 需要渲染场景两遍
  • 软阴影与硬阴影

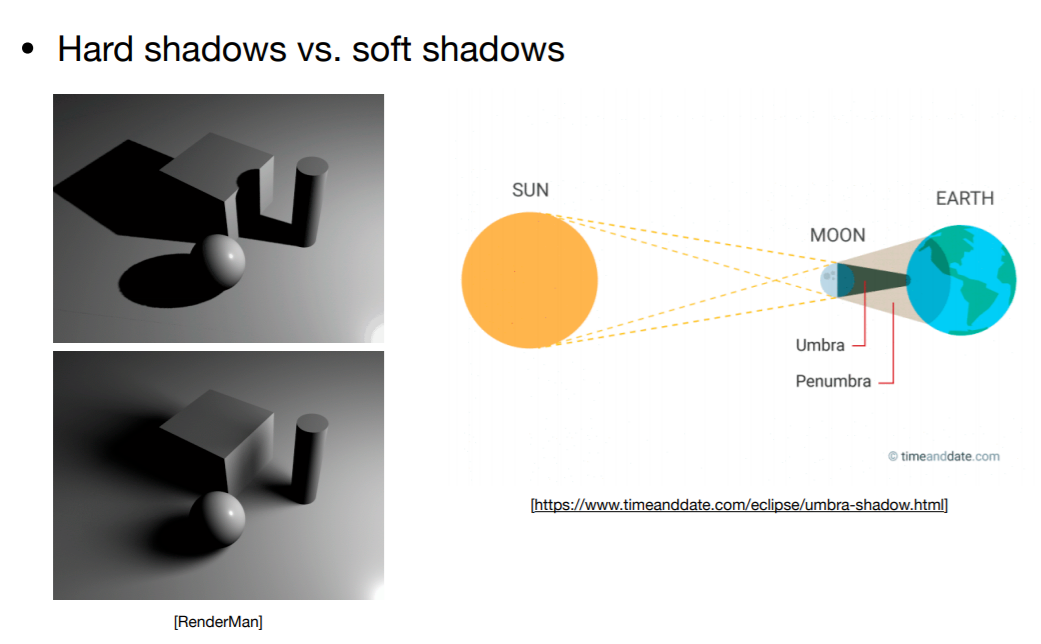
  • 物理上的本影与半影