计算机图形学.李胜.10.高级光照模型与绘制理论

Posted on Edited on In Views:
BRDF反射模型、反射方程、绘制方程

BRDF反射模型

  • Bidirectional Reflectance Distribution Function
  • 双向反射率分布函数
  • 用来描述物体的材料属性，表示光如何从一个表面反射出去
  • 输入参数：5
    • 入射光和发射光的方位角 \(\phi\)、仰角 \(\theta\)
    • 入射光的波长 \(\lambda\)
  • 输出一个无单位的值
    • 表示对于给定的入射方向，在发射方向反射出去能量的比例
    • BRDF 给出了入射光子在某一方向离开的概率
      • 立体角对应的面上的能量
  • incoming / outgoing

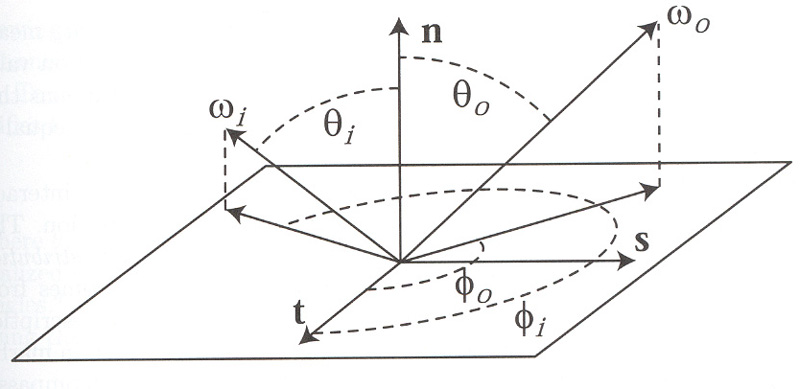
  • BRDF 描述了入射辐射亮度和发射辐射亮度是如何相互联系的，但没有解释材料是如何在物理上与光相互作用的

BRDF 的性质

  • Helmholtz互反定理（Helmholtz reciprocity）
    • Value of BRDF remains unchanged if the incident and outgoing directions are interchanged
    • 输入和输出角切换后函数值相同
  • 能量守恒定律
    • the total amount of power reflected all directions must be less than or equal to the total amount of power incident on the surface
    • 发射的能量小于等于入射的能量

BRDF 的例子

Diffuse 漫反射

\[ F_r=\dfrac{\rho_d}{2\pi} \]

  • \(\rho_d\) 表示出射光占入射光的比例，0-1

specular 镜面高光

\[ Exitant\ direction:R=2(N\cdot\Psi)N-\Psi \]

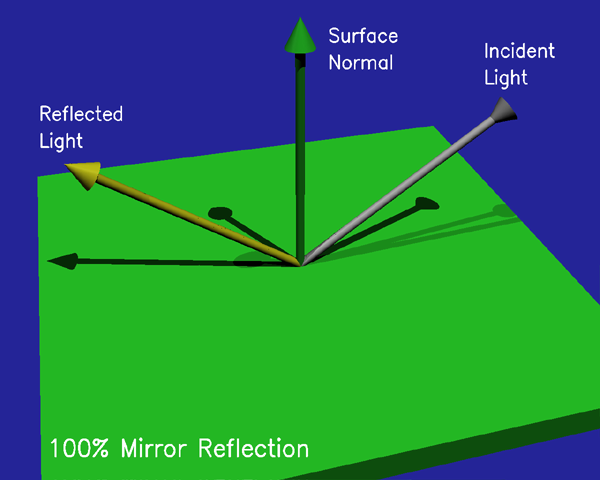
一般物体

BSSRDF

  • BRDF 是更一般方程双向表面散射反射率分布函数的一种逼近
    • Bidirectional Surface Scattering Reflectance Distribution Function (BSSRDF)
  • BRDF 没有考虑表面内光的散射
    • 大理石
  • BSSRDF 通过把入射光的位置和发射光的位置作为函数的输入覆盖了散射现象
    • 它描述的是光从入射方向在表面的某一点入射，然后在另一点沿发射方向发射的比率

反射方程

  • Reflectance Equation
  • 给定一 BRDF 和入射辐射亮度分布，反射方程决定了表面在给定视域方向的发射辐射亮度。它通过在表面的半球面上对所有方向的入射辐射亮度进行积分得到

\[ L(\theta_o,\phi_o)=\iint_{\Omega}f(\theta_o,\phi_o,\theta_i,\phi_i)L(\theta_i,\phi_i)\cos(\theta_i)d\sigma(\theta_i,\phi_i) \]

  • \(i,o\) 入射出射方向
  • \(f\) 表示 BRDF
  • \(L\cos(\theta_i)\) 将光线转化为正向入射
  • 在半球面上积分
  • 该方程对三个颜色分量单独计算

点光源的反射方程

  • 点光源，简化为

\[ L(\theta_o,\phi_o)=f(\theta_o,\phi_o,\theta_i,\phi_i)L(\theta_i,\phi_i)\cos(\theta_i) \]

  • \((\theta_i,\phi_i)\) 表示光源方向
  • 向量表示

\[ L(\vec{\omega_o})=f(\vec{\omega_o},\vec{\omega_i})L(\vec{\omega_i})(\vec{n}\cdot\vec{\omega_i}) \]

BRDF分布图

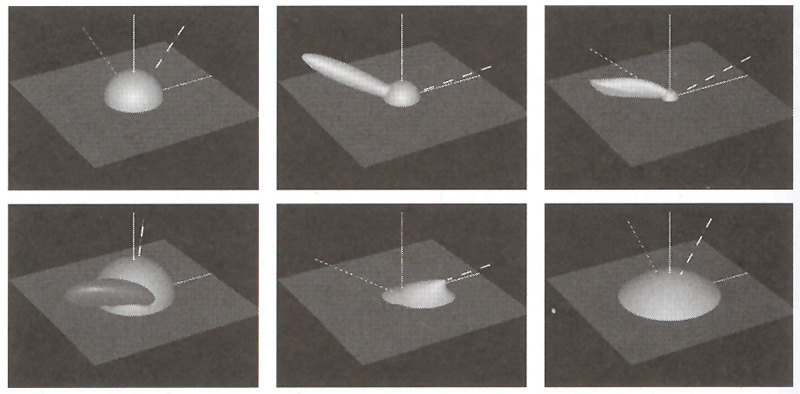
  • 理解 BRDF 的一种方法为把入射方向保持恒定，然后观察其输出结果。对于给定方向的入射光，发射能量的分布不同。
  • 交点附近的球面部分为漫反射项。椭圆形部分的为反射叶(reflectance lobe)（镜面项），通常在入射光的反射方向。
  • Torrance-Sparrow 模型：镜面高光并非在反射方向最强
漫反射表面 Phong/Blinn 高光 + 漫反射 Torrance-Sparrow模型
Ward’s各向异性模型 Hapke的BRDF模型 Lommel-Seeliger散射模型

微面元

  • microfacet
  • 微面元是物体表面上一种微小的、平坦的镜面，具有随机的大小和角度

  • 在 BRDF 模型中，一般处理成高斯分布
    • 处理方便
  • 微面元描述典型反射
    • 镜面反射可以用一些微面元的直接反射来描述
    • 漫反射可以用微面元间的相互反射来描述
    • 微面元之间还可以互相投射阴影
  • 当微面元的大小与光的波长相近时，还有一个重要概念 height correlation, 可用来模拟干涉、衍射等物理现象

菲涅尔反射

  • Fresnel Reflectance
  • 塑料、玻璃和水等绝缘体或电介质材料
  • 当电介质材料以接近掠角（Grazing angle）的角度观察时，反射会更厉害（但对于金属，该角度引起的反射变化相对较小）
    • 当用最浅的掠角时，所有的材料变成全反射
  • 现象
    • 手拿一本书，对准计算机的显示器，以很浅的角度去看其中的页面，在一个极端浅的角度，你可以看到屏幕在书上的反射

菲涅尔反射公式

  • 菲涅尔反射的公式与折射率、衰减系数、入射角有关
    • 绝缘体的折射率可设成是1.5
    • 若衰减系数未知，可设置为0
  • 菲涅尔反射公式如下

\[ F=\dfrac{1}{2}\dfrac{(g+c)^2}{(g-c)^2}(1+\dfrac{[c(g+c)-1]^2}{[c(g-c)+1]^2}) \]

\[ c=\vec{v}\cdot\vec{h} \]

\[ g=\sqrt{n^2+c^2-1} \]

  • \(\vec{v}\) 为视线矢量，\(\vec{h}\) 为半角矢量，\(n\) 为折射率
    • \(\vec{h}=\dfrac{1}{2}(\vec{v}+\vec{l})\)
    • 入射光矢量、视线矢量
  • 一个 \(n=1.5\) 的例子

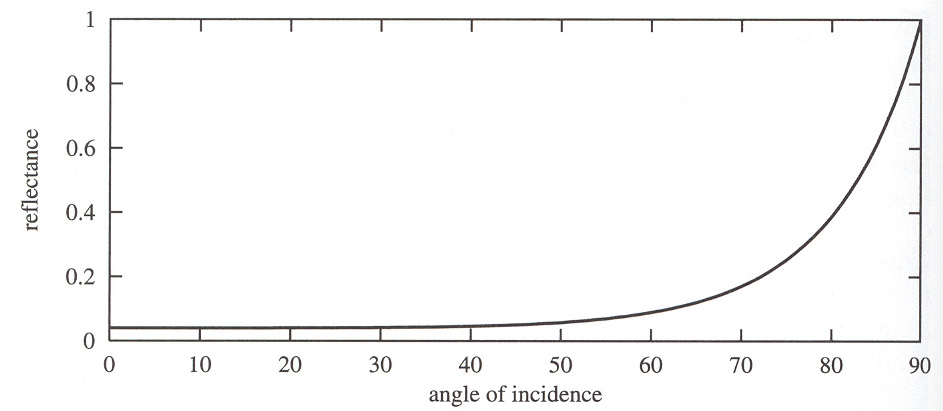
Torrance-Sparrow / Cook-Torrance BRDF

  • 描述较光滑的表面
  • 基于微面元
    • 通过光线在微面元上的相互作用计算出一个衰减因子 \(G\)
      • geometric attenuation factor
      • 0-1：total shadowing - no shadowing

光线在微面元上传播的一些情况

unblocked

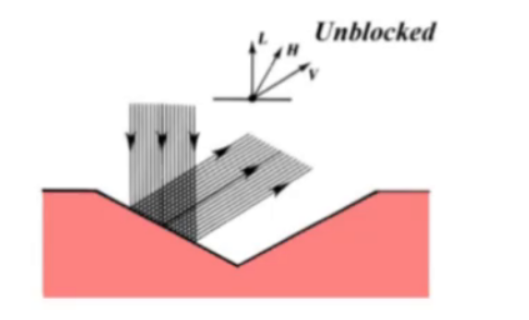
masking

  • 部分/全部出射光线被遮挡

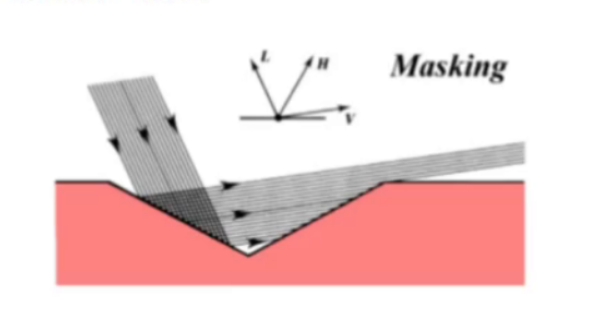
shadowing

  • 入射光线部分/全部被遮挡

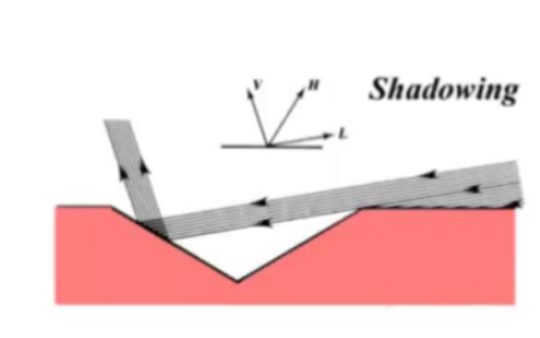
BRDF

\[ \dfrac{F(l,h)G(l,v)D(h)}{4(n\cdot l)(n\cdot v)} \]

  • \(l\)：光源方向，\(v\)：视线方向，\(n\)：法向，\(h\)：半角矢量
  • \(G(l,v)\)：Geometric Attenuation Factor
    • reduces the output based on the amount of shadowing or masking that occurs
  • \(F(l,h)\)：Fresnel term（菲涅尔反射）
  • \(D(h)\)：Distribution
    • distribution function determines what percentage of microfacet are oriented to reflect in the viewer direction
  • \((n\cdot l)\)：How much of the macroscopic surface is visible to the light source
  • \((n\cdot v)\)：How much of the macroscopic surface is visible to the viewer

如何获取 BRDF

  • BRDF 理论模型的一个问题是它们不能表示特定的材料
  • 获取真实表面的 BRDF
    • 角度测定法（goniometers）
    • 双向反射计成像法（imaging bidrectional reflectometers）
    • 基于图像的方法（image-based methods）
  • 公开数据库下载
    • http://people.csail.mit.edu/wojciech/BRDFDatabase/
      • 无法访问？

BRDF 绘制实现方法

  • 应用 BRDF 的直接方法为计算顶点的颜色并把结果传到流水线。但其缺点是：如果 BRDF 反射在一些象素上的变化速度太快，线性插值会导致丢失或过分突出这种反射变化。一个解决方法是把表面加细，但会降低算法的性能。
  • 对于给定的材料，如果有一种存取快速的简凑的表示方法，可以带来如下好处
    • 避免精确理论模型的计算耗费
    • 减少存贮量
    • 减少实验获取BRDF中的噪声
  • 在实时绘制中，主要采用两种简凑的BRDF表示方法
    • Factorization 因数分解法
    • Environment map filtering 环境图滤波

因数分解法

  • 一种表示 BRDF 的方法为把 BRDF 表示成乘积项的和（而不是一系列基函数的加权和），其中每个乘积项包含两项
  • 思想：把 BRDF 转化为一系列二维纹理对。每对纹理通过四维参数存取（2个入射角和2个发射角），返回的纹理值相乘后再相加，得到象素的颜色
  • 初始的 BRDF 有两个方向矢量，入射矢量和发射矢量。因数分解法就是把 BRDF 表示成简单函数对乘积的和

\[ f(\vec{\omega_i},\vec{\omega_o})\approx\sum_{j=1}^np_j(\vec{\omega_i})q_j(\vec{\omega_o}) \]

  • 因数分解法蕴涵的思想为把入射和发射方向映射为纹理上的象素，使得上式中的 n 尽量小，并且方向矢量可以通过纹理的线性插值来得到
  • 存取的纹理与环境映照具有相同的形式：球面图、抛物面图、立方体图
    • 其中立方体图的质量最高
  • 我们的目标是构造纹理对
    • 入射纹理：通过入射方向存取
    • 发射纹理：通过发射方向存取
  • 在实践中，我们发现这种参数化结果并不好，会导致需要很多纹理对（n很大）才能较好地逼近 BRDF。在三角形内的线性插值结果也不好，会导致严重的误差
  • 好的参数化方法与材料的类型有关（并非完全是一个科学问题）

矩阵分解计算纹理对

  • 为了计算纹理对，需要构造一大型矩阵（可以采用预计算的方法）
  • 入射纹理的每个纹素表示该矩阵的行下标，发射纹理的每个纹素表示该矩阵的列下标
  • 矩阵的每个元素表示 BRDF 的反射系数值
  • 矩阵分解通常采用两种方法
    • 奇异值分解(SVD, Singular Value Decomposition),
    • 规范化分解(ND, Normalized Decomposition)
  • 把分解得到的行矢量和列矢量对存入纹理对，便得到我们所需要的纹理对
  • 规范化分解的缺点是结果不太精确，但比SVD简单、存贮量小，并且纹理值都是正的
    • 用的不多
  • 矩阵分解可看成是一种数据压缩方式
    • 四维的 BRDF 转化为纹理对，然后由图形硬件进行解压。由于纹理可以用球面图或抛物面图来表示，因此该技术可在任何图形硬件上运行

缺点

  • 对于每个光源，至少需要一对纹理
  • 只适合点光源和方向光。不能捕获从面光源、天空光和其它物体来的辐射亮度

环境图滤波

  • BRDF 是一个方向，对多个反射方向进行滤波（漫反射效果）
  • 前面我们讲过，环境图可以用来绘制理想的发光表面（perfectly shiny surface）
  • 这个概念同样可以推广到光滑面（glossy surface）和漫反射面
  • 为了模拟表面不同程度的粗糙度，我们可以对纹理的环境表示进行滤波
    • 通过对环境图进行模糊操作，我们可以使得镜面反射呈现**粗糙的视觉效果*
  • 理论上，模糊操作应以非线性的方式进行。也就是说，纹理的不同部分应以不同的方式进行模糊。但因为整体的反射效果通常比精确的反射更重要，所以我们可以直接采用对环境图进行均匀模糊的方法
  • 一个物理上更真实的方法为采用 Phong 镜面方程来对环境图进行滤波。镜面叶决定采样环境映照中的哪些纹素，并决定每个纹素的相对贡献
  • 滤波方式
    • 理想镜面反射
    • 反射光线的镜面叶
    • 对表面上的余弦加权半球面进行求和来得到漫反射分量中入射光的贡献

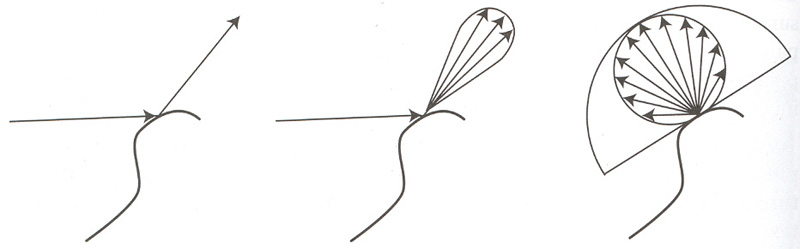
  • 其思想是把环境映照 EM 看成是罩在物体外面的一个球面。EM 上的每个纹素表示球面上的不同面积，其值为常数。由纹素构成的四边形实际上描述了一个球面四边形，其面积可用两个平面三角形来简单逼近。为了建立模拟表面模糊效果的图，首先进行预处理，计算纹素四个角点的单位化法向和纹素的面积。
  • 算法思想
    • 对于每个反射方向，找到每个EM纹素对该方向的贡献
    • 假设反射方向附近有一个光源，直接从反射方向来的光具有最大的贡献，越偏离该方向, 贡献越小
    • EM纹素的面积乘上该纹素的 BRDF 贡献给出了该纹素的相对影响，把结果相加来计算q。s为加权贡献的和
    • 最后的结果 q/s 为在反射方向叶上积分得到的整体颜色

绘制方程

反射方程

  • Reflected Light(Output Image)
    • Emission
    • Incident Light (from light source) x BRDF x Cosine of Incident angle
  • 自发光 + 反射光

点光源

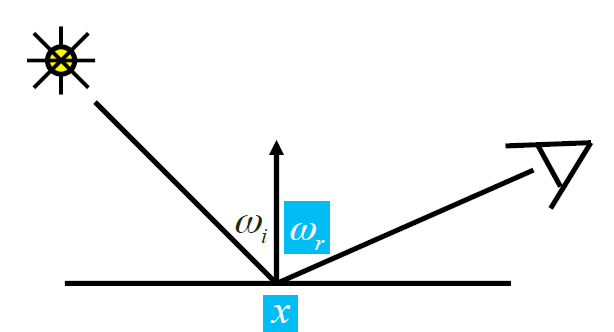\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+L_i(x,\vec{\omega_i})f(x,\omega_i,\omega_r)(\omega_i\cdot n) \]

多光源

\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+\sum L_i(x,\vec{\omega_i})f(x,\omega_i,\omega_r)(\omega_i\cdot n) \]

面光源

  • 立体角积分

\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+\int_\Omega L_i(x,\vec{\omega_i})f(x,\omega_i,\omega_r)(\omega_i\cdot n)d\omega_i \]

全局光照明

  • 其他表面的反射光
  • $ L_r(x',-)$ 未知

\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+\int_\Omega L_r(x',-\vec{\omega_i})f(x,\omega_i,\omega_r)(\omega_i\cdot n)d\omega_i \]

渲染方程

  • 上面的全局光照明
  • 直接光与间接光
    • Direct (local ) illumination
      • Light directly from light sources
      • No shadows
    • Indirect (global ) illumination
      • Hard and soft shadows
      • Diffuse interreflections (radiosity)
        • interreflections ：相互反射
      • Glossy interreflections (caustics)
        • caustics：焦散
  • 挑战：入射光出射光互相依赖
    • To evaluate the reflection equation the incoming radiance must be known
    • To evaluate the incoming radiance the reflected radiance must be known
  • Surface Balance Equation
    • [outgoing] = [emitted] + [reflected]
    • [outgoing] = [emitted] + [reflected] + [transmitted]
      • BTDF：透射光（下面透射上来、透射下去）

\[ L_o(x,\vec{\omega_o})=L_e(x,\vec{\omega_o})+L_r(x,\vec{\omega_o})+L_t(x,\vec{\omega_o}) \]

\[ L_r(x,\vec{\omega_o})=\int_{H_+^2} L_i(x',\vec{\omega_i})f_r(x,\omega_i\to\omega_o)(\cos\theta_i)d\omega_i \]

\[ L_t(x,\vec{\omega_o})=\int_{H_-^2} L_i(x',\vec{\omega_t})f_r(x,\omega_t\to\omega_o)(\cos\theta_t)d\omega_t \]

  • 可以利用法向合并

\[ H_+^2(n):\omega_o\cdot n(x)>0\\ H_-^2(n):\omega_o\cdot n(x)<0 \]

\[ L(x,\vec{\omega})=L_e(x,\vec{\omega})+\int_{H^2} L(x^\ast(x,\omega'),\vec{\omega})f_r(x,\omega'\to\omega)(\cos\theta')d\omega' \]

  • \(x^\ast(x,\omega')\) 中间包含路径衰减等因素（传输因子）
  • 推到得到矩阵形式

\[ l(u)=e(u)+\int l(v)K(u,v)dv \]

\[ L=E+KL \]

  • 矩阵 \(K\) 表示在光的传播过程中其他各点的贡献
  • L, E are vectors, K is the light transport matrix

解渲染方程的方法

  • All global illumination methods try to solve (approximations of) the rendering equation
    • Too hard for analytic solution: numerical methods
    • General theory of solving integral equations
  • Radiosity (usually diffuse surfaces)
    • General class numerical finite element methods (divide surfaces in scene into a finite set elements or patches)
    • Set up linear system (matrix) of simultaneous equations
    • Solve iteratively
  • ray tracing and extensions
    • \(L=(I-K)^{-1}E\)
    • \(L=(I+K+K^2+K^3+K^2+\cdots)E\)
      • \(E\)：Emission directly（From light sources）
      • \(KE\)：Direct Illumination on surfaces
      • \(KE^2\)：Global Illumination (One bounce indirect)[Mirrors, Refraction]
      • \(KE^3\)：Global Illumination (Two bounce indirect)[Caustics etc]
    • OpenGL：L=E+KE
  • 将立体角转变为我们常用的离散面片

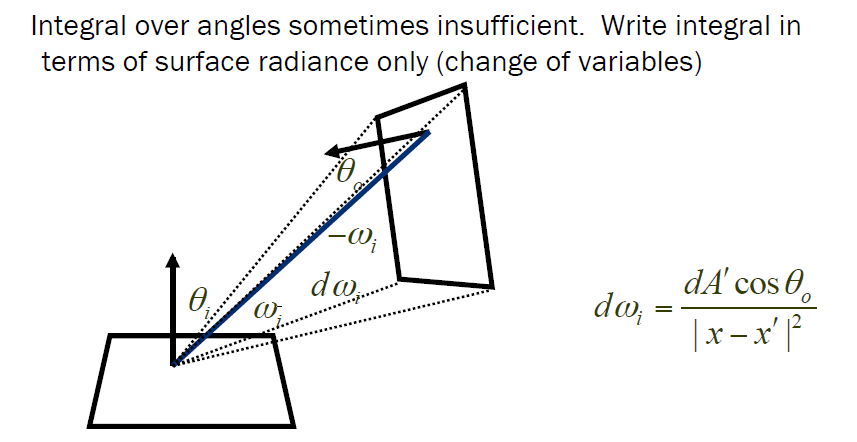
  • 加入可见性检测 \(V(x,x')\)

\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+\int_\Omega L_r(x',-\vec{\omega_i})f(x,\omega_i,\omega_r)\cos\theta_id\omega_i \]

\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+\int_\Omega L_r(x',-\vec{\omega_i})f(x,\omega_i,\omega_r)V(x,x')\dfrac{\cos\theta_i\cos \theta_0}{|x-x'|^2}dA' \]

\[ L_r(x,\vec{\omega_r})=L_e(x,\vec{\omega_r})+\int_\Omega L_r(x',-\vec{\omega_i})f(x,\omega_i,\omega_r)V(x,x')G(x,x')dA' \]