计算机图形学.李胜.09.纹理映射
纹理及纹理映射基本原理
纹理
- 纹理 / 贴图
- 纹理是物体表面的细小结构
- 颜色纹理、几何纹理
- 纹素:纹理像素
颜色纹理
- 光滑表面的花纹、图案
几何纹理
- 基于物体表面的微观几何形状的表面纹理
- 粗糙的表面
- 例:桔子表面的皱纹)
- 修改几何、法向扰动
模拟物体表面细节
模拟细节多边形
- 根据代生成的纹理构造细节多边形
- 将细节多边形贴到物体表面
- 很麻烦

- 例如上图中的前向面
- 如果使用纹理贴图的话,只需要两张图即可(底层浅灰色+T的深灰色)
- 如果使用模拟多边形的话,需要将整个面划分为若干个三角形,将这些三角形分别着色(灰/深灰)
纹理映射
纹理的表示
图象纹理
- 将二维纹理图案映射到三维物体表面,绘制物体表面上一点时,采用相应的纹理图案中相应点的颜色值
函数纹理
- 用数学函数定义简单的二维纹理图案,如方格地毯
- 或用数学函数定义随机高度场,生成表面粗糙纹理即几何纹理
- 噪声
纹理映射
- 当物体表面是多边形时,直接给定多边形顶点的纹理坐标
- 当物体表面是参数曲面时,给定参数与纹理坐标之间的关系
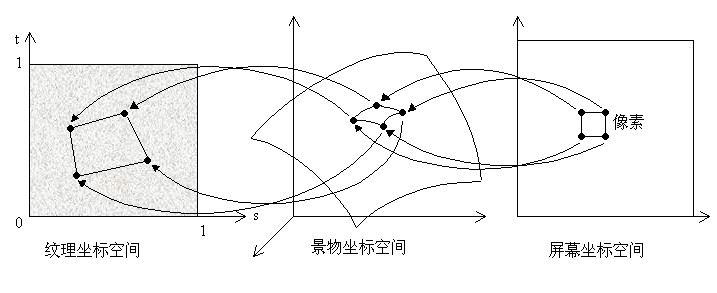
纹理映射的步骤
- 将屏幕像素的四个角点映射到景物坐标空间中可见的物体表面上
- 将景物坐标空间映射到纹理坐标空间
- 将像素所对应的纹理坐标空间中的四边形内的所有纹素的值作加权平均,结果作为物体表面的漫反射系数参与颜色计算
- 加权平均只是其中一种方法
- 作为漫反射系数参与计算只是其中一种用途
一些纹理映射
- 纹理图象模拟国际象棋上黑白相间的方格
常用的纹理映射方法
圆柱面映射
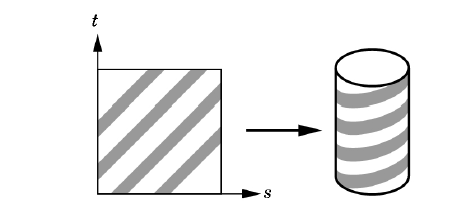
- 参数方程
\[ \left\{ \begin{array}{**lr**} x=\cos(2\pi u) &0\le u\le1\\ y=\sin(2\pi u) &0\le v\le1\\ z=v \end{array} \right. \]
- 反求参数
\[ (u,v)= \left\{ \begin{array}{**lr**} (y,z)&,x=0\\ (x,z)&,y=0\\ (\dfrac{\sqrt{x^2+y^2}-|y|}{x},z)&,else \end{array} \right. \]
球面映射
- 参数方程
\[ \left\{ \begin{array}{**lr**} x=\cos(2\pi u)\cos(2\pi v) &0\le u\le1\\ y=\sin(2\pi u)\cos(2\pi v) &0\le v\le1\\ z=\sin(2\pi v) \end{array} \right. \]
- 反求参数
\[ (u,v)= \left\{ \begin{array}{**lr**} (0,0)&,(x,y)=(0,0)\\ (\dfrac{1-\sqrt{1-(x^2+y^2)}}{x^2+y^2}x,\dfrac{1-\sqrt{1-(x^2+y^2)}}{x^2+y^2}y&,else \end{array} \right. \]
两步法纹理映射
- Bier 和 Sloan 提出,应用于三维曲面上
步骤
- 先映射到一个简单的三维曲面上,如平面,柱面,球面或者立方体上(中介曲面)
- 把变形后的映射结果映射到最终曲面上
从中介曲面到物体表面的映射方式
- 反射光线法
- 物体法向法
- 物体中心法
- 中介表面法向法
一些问题
- 大片屏幕区域使用同一个纹素(色块效应)
- 一个像素对应很大区域的纹素
- 纹理的走样
特殊类别纹理映射
环境映射
- Blinn 和 Newell 提出
- 环境被映照到一个大的球面上
解决的问题
- 如果目的是为了渲染场景中的一个杯子(小物体),若利用光线跟踪方法,需要对整个场景进行建模渲染,计算量极大
- 效果比光线跟踪差,但是计算量要小很多
方法
- 从视点出发,向待绘制的物体表面上一点发出一条光线,求在该点的反射光线与环境球面的交点
- 平面情况处理,用虚视点方法
- 环境纹理的获取
- 实拍
- 生成
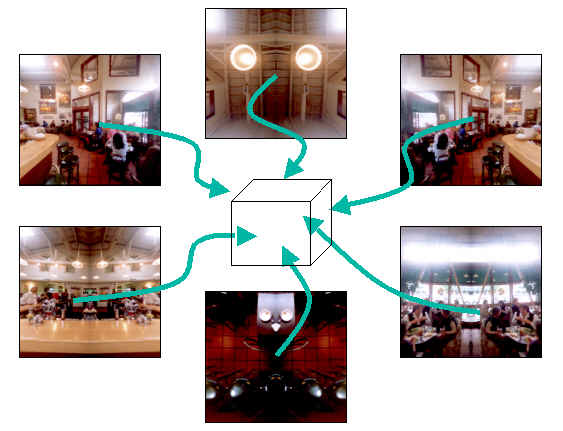
一种环境映射 cube map

过程纹理
- 一个小的纹理样本,通过一些简单的变化(相关到那时不一样)形成一片纹理
- 例如:斑马纹、豹纹等
- 木头纹理
- 三维体纹理
- 二维纹理图象或纹理函数 sweep(平移、旋转等)
- Fourier合成
- 噪声函数随机合成
3D 体纹理
- 动物毛皮(制作得很真实极难)
- 精细建模:计算量很大
- 不精细建模:整体效果粗糙,边界粗糙
体纹理绘制方法
- 基于 shells 的绘制策略
- 初始的带点的一张图片,通过微小的偏移形成毛发效果
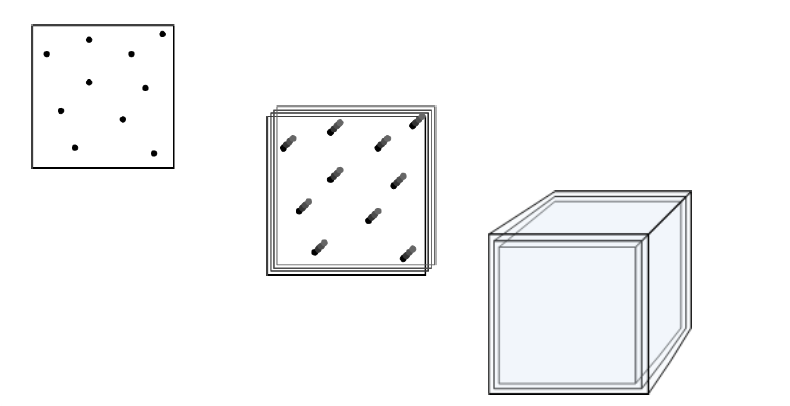
- 毛发绘制真实感
- 加入阴影
- 可变长度
纹理反走样
MipMapping 反走样
- 图象金字塔
- 从高分辨率到低分辨率,分层存储
- 纹理颜色的平均,正方形滤波器作卷积
- 解决的问题:纹素分辨率与渲染图像分辨率不匹配
- 假使原先是匹配的,视点的改变也会导致不匹配(距离变化)

- 使用的时候按照距离的远近选择不同的分辨率
- 例如:每次缩小一半
- RGB 3通道,一个方便的存储方式
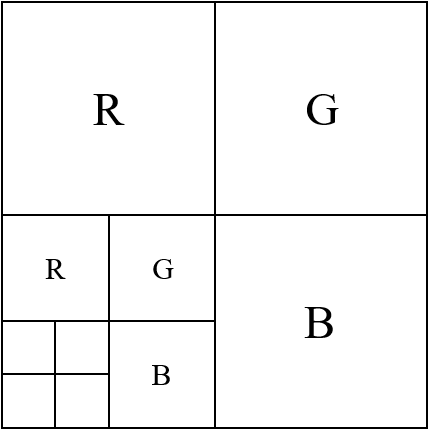
- 使用 mipmap 之后过度更加柔和
SAT 表反走样
- 将屏幕像素的4个顶点做映射,找到在纹理中中对应的4个点,对这4个点围成的区域中的纹素表示屏幕像素的纹理
- 表示方式:均值、滤波等
- 相对低效,因此会采用矩形近似的方法(横平竖直的矩形)
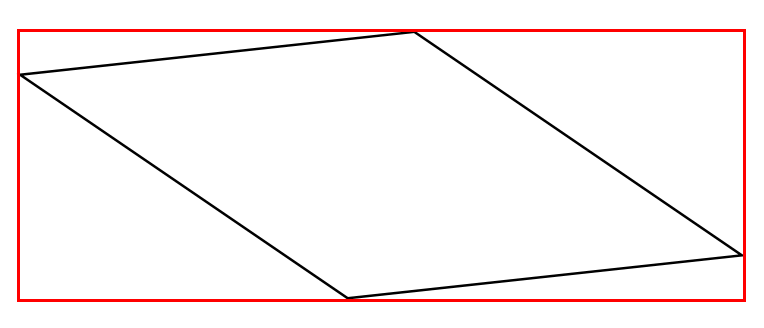
- 加速
- 动态规划加速
- 每个顶点记录和原点组成的矩形内像素的和
三维纹理域的映射
- 物体中每一个点 \((x,y,z)\) 均有一个纹理值 \(t(x,y,z)\),其值由纹理函数 \(t(x,y,z)\) 唯一确定
- 三维纹理映射的纹理空间定义在三维空间上,与物体空间维数相同,在纹理映射的时候,只需把场景中的物体变换到纹理空间的局部坐标系中去即可
几何纹理之法向扰动法
- 效果很棒
- 目标:产生几何纹理,模拟凸凹不平的物体表面
- 应用:自然界中植物的表皮等
- 方法:对物体表面微观形状进行扰动
bump map(凹凸贴图)
- 凹凸贴图是指计算机图形学中在三维环境中通过纹理方法来产生表面凹凸不平的视觉效果。它主要的原理是通过改变表面光照方程的法线,而不是表面的几何法线来模拟凹凸不平的视觉特征,如褶皱、波浪等等。凹凸贴图的实现方法主要有:偏移向量凹凸纹理和改变高度场(百度百科)
法向扰动
- 对物体表面几何性质作微小扰动,产生凹凸不平的细节效果,给物体表面图象加上一个粗糙的外观
- 物体表面上的每一个点 \(P(u,v)\),都沿该点处的法向量方向位移 \(F(u,v)\) 个单位长度,新表面位置 \(\widetilde{P}(u,v)=P(u,v)+F(u,v)*N(u,v)\)
- 新表面的计算方法:通过对两个偏导数求叉积得到
\[ \widetilde{N}=\widetilde{P_u}\times\widetilde{P_v}\\ \widetilde{P_u}=\dfrac{d(P+FN)}{du}=P_u+F_uN+FN_u\\ \widetilde{P_v}=\dfrac{d(P+FN)}{dv}=P_u+F_vN+FN_v\\ \]
- 由于 \(F\) 很小,作近似计算
\[ \widetilde{N}\approx(P_u+F_uN)\times(P_u+F_vN) \]
几何纹理实现
- 扰动后的法向量单位化,用于计算曲面的明暗度,产生凹凸不平的几何纹理
- \(F\) 的偏导数的计算,可以用中心差分实现
- 几何纹理函数定义可以用统一的图案纹理记录
- 图案中较暗的颜色对应较小 \(F\) 值
- 较亮的颜色对应较大 \(F\) 值
- 把各象素的值一个二维数组记录下来
- 在实际操作中直接给每个点新的法向即可(即上述说的记录)
parallax mapping & relief mapping
parallax mapping
- 视差贴图
- 普通纹理映射存在的问题:立体感不强
- 原因是因为之前的纹理并没有考虑实际场景中的物体内容
- 在视角变化下,实际看到的纹理内容会有变化
- 实际看到的是 \(T_{ideal}\) 而不是 \(T\)
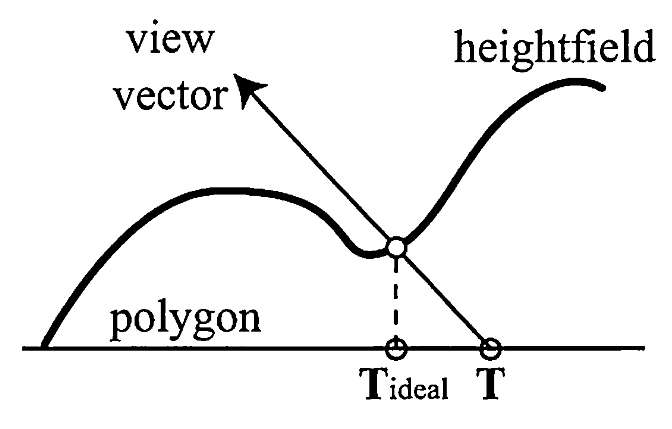
- 视差贴图的纹理与内容相关,估计/计算真正的纹理位置
- Kaneko (2001)
- take an educated guess of what should be seen in a pixel by
examining the height of what was found to be visible
- 在高度场(height field)中检测像素的可见性
- Height field texture can be stored in unused color channel (alpha)
- 将高度场信息保存在透明度通道
- take an educated guess of what should be seen in a pixel by
examining the height of what was found to be visible
方法1
- 直接给定一个 offset(箭头表示视线)
\[ P_{adj}=P+\dfrac{h\cdot v_{xy}}{v_z}=p+h\tan\theta \]
- \(v_z,v_{xy}\) 视线的偏移量
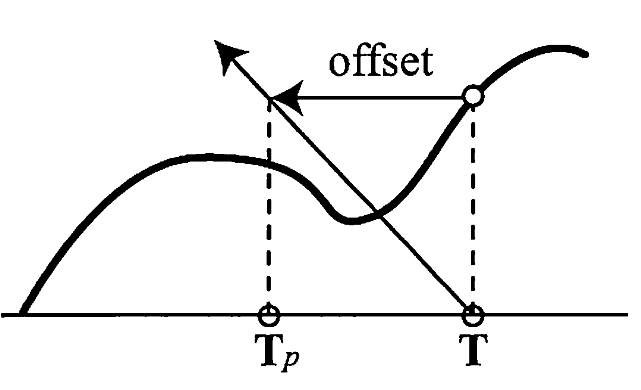
- 不准确
- 尤其是浅视角(Shallow viewing angle)的时候,\(v_z\) 很小,偏移量极大
方法2
- offset-limited,对 offset 进行限制没最多让其为 h
- 对 \(v_{xy}\) 进行归一化(0-1)
\[ P_{adj}=P+h\cdot v_{xy} \]
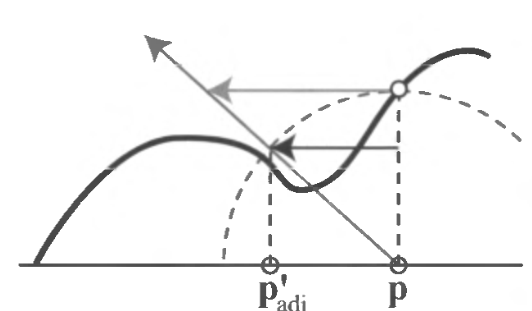
- 纹理内容 \(\rightarrow\) 高度场 \(\rightarrow\) 新的纹理坐标
同类技术的多种名称
- Independently discovered under different names
- parallax occlusion mapping
- relief mapping
- steep parallax mapping
- inverse displacement mapping
- 改进的方向:快速、效果
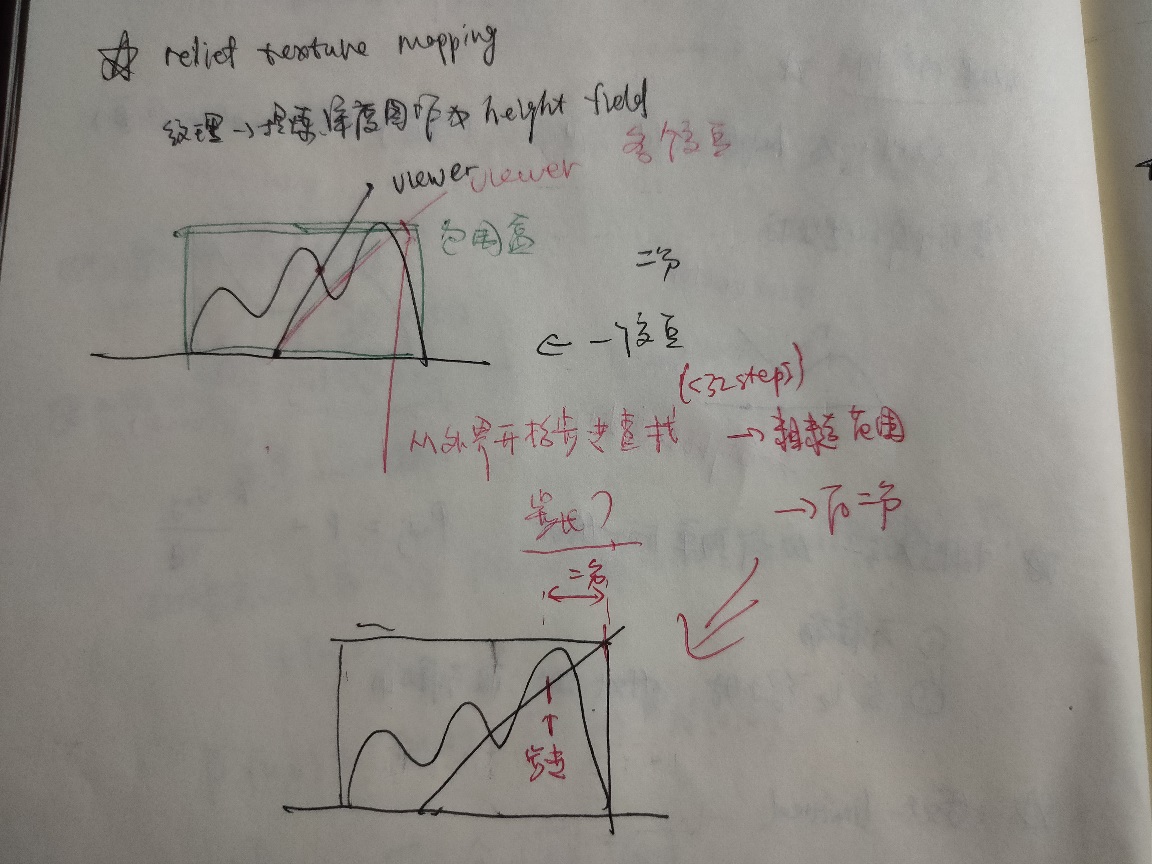
Relief Texture Mapping
- 纹理 \(\rightarrow\) 提炼出深度图作为高度场信息
- 如果视线和高度场只有一个交点,通过二分的方式进行查找交点,从而找到正确的纹理坐标
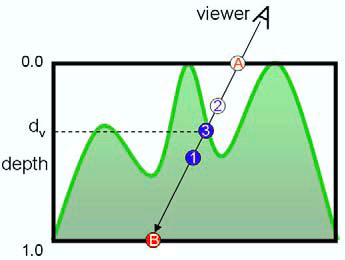
- 如果交点不止一个怎么办?
- 从外界开始步进探测视线与高度场的第一个交点(粗糙查找)
- 步进找到粗糙的位置之后,进行二分检测(精确)
- 32 步一定能找到
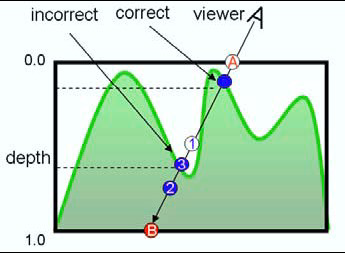
阴影计算
- 在找到位置之后,直接计算光照
- 在找纹理位置的同时就已经解决了阴影的问题
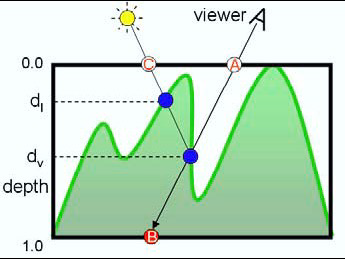
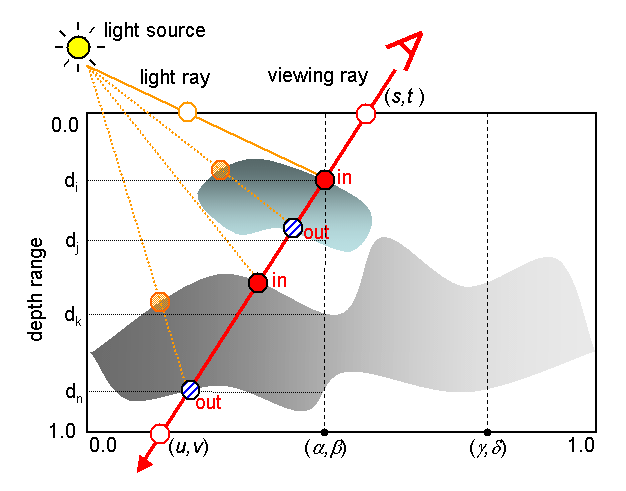
更加复杂的纹理
- Relief mapping of non-height-field surface details
- Fabio Policarpo, Manuel M. Oliveira
- 多层次高度场
其他
- 遵照物理模型的自然现象模拟
- 夜空光照
- 不同时刻不同散射系数的天空光
- 天空体积云及光照
- 云状物及爆照效果
- 火焰
- 烟雾
- 间接阴影
- 复杂材质光照特性
- 焦散
- 半透明材质