计算机图形学.李胜.08.真实感绘制之光照明(2)
整体光照明模型
- 全局光照明 / 整体光照明
- 还要考虑周围环境的光对物体表面的影响(间接光照)
- 光亮平滑的物体会将环境中其它物体映象在表面上
- 透过透明物体可以看到其后的环境景象
- 更精致的真实感图形的绘制还要考虑物体表面的细节纹理(纹理映射)
物体表面入射光的构成
光源直接照射
其他物体的反射光
透射光
- 局部光照明模型仅考虑了 (1)
整体光照明方程
- Whitted 模型
\[ I_\lambda=I_{l\lambda}+K_sC_{c\lambda}I_{s\lambda}+K_tC_{t\lambda}T_{t\lambda} \]
- 局部光照明 + 其他表面光的反射光 + 物体背面的透射光
分类
- 辐射度类
- VPL:Virtual Point Light
- 辐射度方法
- 光线跟踪类
- metropolis light
- photon mapping
- 蒙特卡洛光线追踪
其他概念
- 路径追踪
- 狭义:蒙特卡洛光线跟踪
- 广义:光线跟踪
初级光线跟踪法
- 光线跟踪法
- 1968,Apple A 研究隐藏面消除算法时[APPL68],给出了光线跟踪算法的描述
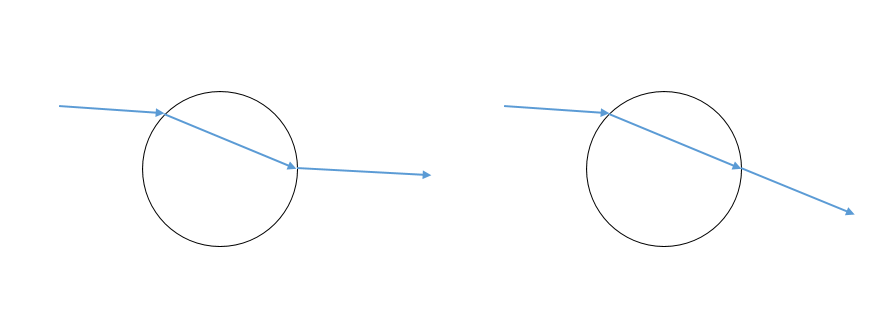
- 1979,Kay 和 Greenberg 的研究考虑了光的折射[KAY79]
- 1980,Whitted 提出了第一个整体光照 Whitted模型[WHIT80]
- 注意光线跟踪不走经典的 pipeline(不同于经典的绘制管线)
- 光的传播过程
- 光源 \(\rightarrow\) 物体表面 \(\rightarrow\) 物体表面 \(\rightarrow\dots\rightarrow\) 物体表面 \(\rightarrow\) 人眼
- 光线跟踪过程——光线传播的逆过程
- 逆过程:不从光源出发,而从视点出发
- 若从光源出发,光线进入人眼的概率极低
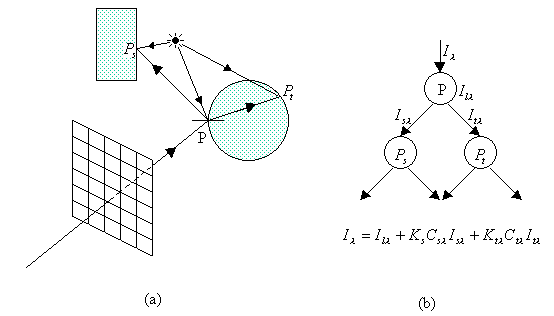
- 是一个递归的过程
- 列出方程,求解
- 模拟解 $ $
- 数值解 \(\times\)
光线跟踪的关键问题
- 光线与物体表面的求交
- 逢交点考察反射和折射
- 阴影测试线
- 判断待计算点是否对光源可见
- 终止条件
- 虽然在理想情况下,光线可以在物体之间进行无限的反射和折射
- 但是在实际的算法进行过程中,我们不可能进行无穷的光线跟踪
- 因而需要给出一些跟踪的终止条件
几种可行的终止条件
- 该光线未碰到任何物体
- 该光线碰到了背景
- 光线在经过许多次反射和折射以后,就会产生衰减,光线对于视点的光强贡献很小
- 小于某个设定值
- 光线反射或折射次数即跟踪深度大于一定值
算法
- 从视点出发,对于视屏上的每一个象素点,从视点作一条到该象素点的射线,调用该算法函数就可以确定这个象素点的颜色
- 对所得的全部交点进行排序,确定可见点
Hall 模型
\[ I=I_{ed}+I_{ld}+I_{ls}+I_{tr} \]
- 环境起的漫反射光亮度 + 光源引起的漫反射光度 + 光源引起的面反射光亮度 + 光源引起的规则透射亮度
- 漫反射 + 透射高光
- 算法一些要点
- 光强衰减:终止条件
- 反射 + 折射
光线与物体表面求交
分类求交
- 光线与平面求交
- 光线与球面求交
- 光线与圆柱面求交
- 光线与二次曲面求交
- 光线与参数曲面求交
光线跟踪算法的加速
- 提高求交速度
- 减少求交次数
- 减少无效求交
- 减少光线条数
- 下采样
- 采用并行算法
减少求交次数
包围盒及层次结构
- 树状结构
- 景物的分布情况,将相距较近的景物组成一组局部场景,相邻各组又组成更大的组,这样,将整个景物空间组织成树状的层次结构
三维 DDA 算法
- 是一个增量算法
- 在一个迭代算法中,每一步的 x、y 值是用前一步的值加上一个增量来获得
- 基本思想
- 将景物空间剖分为网络,由于空间的连贯性,被跟踪的光线从起始点出发,依次穿越它所经过的空间网格,直至第一个交点,这种方法称为空间剖分技术,可以利用这种空间相关性来加速光线跟踪
- 三维 DDA 网格跨越过程,根据 d 空间八叉树剖分技术确定两组始面和终面,并得到最终终面,以此终面为下一个穿越立方格
- 算法对于稠密的场景,选取适当的空间剖分分辨率,可以使算法非常有效
空间八叉树剖分技术
- 空间非均匀网格剖分算法
- 利用了空间连贯性
减少光线条数
- 随机采样:蒙特卡洛采样
- 存在噪声
- 采样点越多,噪声越小
- 神经网络
光线跟踪算法评价
- 实现全局光照明,易于实现光滑物体之间彼此反射的影响,因此显示效果十分逼真
- 有消隐功能:采用光线跟踪方法,在显示的同时,自然完成消隐功能
- 有阴影效果:光线跟踪能完成阴影的生成和显示
- 该算法具有并行性质
- 每条光线的处理过程相同,结果彼此独立,因此可以大并行处理的硬件上快速实现光线跟踪算法
- 光线跟踪算法的缺点是计算量非常大,因此,显示速度极慢,随视点变化而重新计算
Glossy reflection & refraction
- 带有光泽的反射与折射
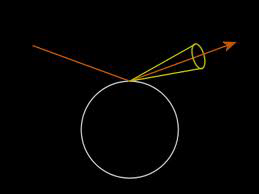
- 控制圆锥顶角的大小,从而控制粗糙度(镜面高光/漫反射)
Photon Mapping
- 光子映射
- 对于透明物体的高光模拟的很好
- 焦散(caustics)
- 焦散是指当光线穿过一个透明物体时,由于对象表面的不平整,使得光线折射并没有平行发生,出现漫折射,投影表面出现光子分散
光线跟踪算法评价
- 较好地模拟了光在光滑物体表面之间的反射和折射现象
- 无法模拟光在景物之间漫反射引起的彩色渗透现象(多重漫反射效果)
初级辐射度算法
- 面对早期的光线跟踪算法只能处理光滑表面而产生的
- 1984,美国 Cornell 大学和日本广岛大学的学者分别将热辐射工程中的辐射度方法引入到计算机图形学中
- 辐射度方法
- 将场景看作一个封闭的系统,能量多重反射,最终达到平衡状态。
- 根据能量守恒定律,计算出每一个表面上的能量
- 选定观察点,采用绘制算法计算出被观察点的颜色
- 与视点无关:广泛用于虚拟漫游
- 主要问题:提高算法效率
主要问题
- 求解场景的辐射度积分方程
- 数值解,利用Gauss-Siedel迭代,Southwell迭代
- 景物表面网格剖分及其形状因子
- 有限元方法,半立方体法
基础理论原理
立体角
- \(d\omega=\dfrac{dS}{r^2}\)

- \(dA_2=dS=rd\theta\ast r\sin\theta
d\psi\)
- 矩形近似,边长为弧长
- \(d\omega=\sin\theta d\theta d\psi\)
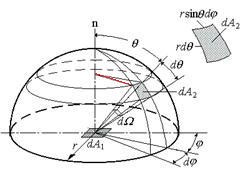
- 球的立体角:\(4\pi\)
光强度
- 光通量:单位时间通过的光能
- 单位:流明
- 图形学中往往讲瞬时,因此往往将光通量和光能混用
- 为表征物体在某一方向上的发光情况,定义某方向上单位立体角内的光通量为该方向上的光强度,记为 \(J\)
- \(J=\dfrac{dF}{d\omega}\)
光亮度
- 将发光面元单位面积上向某方向辐射的光能称为光亮度,记为 \(I\)
- \(I=\dfrac{J\cdot \cos
i}{dS_i}=\dfrac{dF\cdot\cos i}{dS_i\cdot d\omega}\)
- 这里 \(i\) 是法向和辐射法向的夹角
- 光亮度决定了人眼接收的光能的大小和色彩组成
- 光能接受面元所对应的立体角大小
- \(dw'=\dfrac{\cos\theta
dA(x)}{r^2}\)
- \(A(x)\):面积
- \(\theta\):两个面的法向夹角
- \(r\):距离
- \(dw'=\dfrac{\cos\theta
dA(x)}{r^2}\)
辐射度算法的假设
- 假设一封闭环境中,景物表面均为理想漫反射表面
- 景物表面上,每一点向周围各方向辐射的光亮度是相同的
- 表面各点处的光亮度只与位置有关,与辐射的方向无关
- 假设 \(dP\)
为表面某一点处单位面积上朝某辐射方向发出的光通量,则与该点处沿同一方向的光亮度
\(I\) 的关系为
- \(dP=I\cos\theta d\omega\)
- 其中 \(\theta\) 为该点处的法向与辐射方向之间的夹角
- Lambert 漫反射模型
- 则该点处单位面积面元向其四周半空间辐射的总能量(总辐射度 \(B\))
\[ B=\int_{\Omega}dP=\int_{\Omega}I\cos\theta d\omega=I\int_0^{2\pi}\int_0^{\dfrac{\pi}{2}}\cos\theta\sin\theta d\theta d\psi=I\pi \]
- 理想漫反射表面每一点处的辐射度值与光亮度值之比为一常数因子,因而表面各点的光亮度计算可通过求解整个场景的辐射度方程而得到
- 假设周围环境为一封闭系统,则表面上每一点处微面元向周围环境辐射的能量由它自身所具有的辐射光能和它接受来自环境中其他景物表面向该点辐射的光能组成
- 周围环境入射到微面元上的光能为 \(H(x)\)
- 该表面在此处的漫反射率 \(\rho(x)\)
- 则微面元对环境入射光能的反射而产生的那部分辐射光能为 \(\rho(x)H(x)\)
- 由此,此点处的辐射度满足 \(B(x)dA(x)=E(x)dA(x)+\rho(x)H(x)\)
- \(dA(x)\) 为微面元 \(dS(x)\) 的面积
- \(E(x)\) 为该表面在 \(x\) 点处的自身辐射度
- 若该表面为漫反射光源,\(E(x)>0\) ,否则 \(E(x)=0\)
- 自发光 + 周围照射
- 可以对每个面元离散化,使用矩阵求解
\[ \begin{bmatrix} B_1\\ B_2\\ \vdots\\ B_n \end{bmatrix} = \begin{bmatrix} E_1\\ E_2\\ \vdots\\ E_n \end{bmatrix} + \begin{bmatrix} &\cdots\\ \rho_iF_{i1}&\cdots&\rho_iF_{in}\\ &\cdots\\ \end{bmatrix} \begin{bmatrix} B_1\\ B_2\\ \vdots\\ B_n \end{bmatrix} \]
- 辐射度算法:色彩柔和(基于漫反射)
其他
- Fluoresence(荧光效果)
- 海面模拟
- 折射:单层 / 双层
- 入射、出射的折射