计算机图形学.李胜.08.真实感绘制之光照明(1)
真实感绘制流程
- 动机:图形真实感的需求
- 真实感:产生幻觉(illusion)
- 基于用户评估,没有一个确定的标准
- 例子:树皮
- 光线:产生阴影
- 边界:粗糙的感觉
光照明模型发展历史
- 早期光照明模型
- 基于经验
- 只能反映光源直接照射的情况
- 比较精确的模型
- 模拟物体之间光的相互作用
- 间接光照
- 更精确的模型
- 模拟物体自身的光照相互作用
- 模拟光源至物体表面以及物体表面至视点之间光的传播
- 光传播的介质(雾)、物体表面形态、视点位置变化、体数据
- 2005 siggraph achievement:Nishita 东京大学
- 截止:光在大气中传播的模拟
- participating media:参与介质
真实感图形绘制的四个步骤
3D流水线
- 三维形体 \(\rightarrow\) 变换 \(\rightarrow\) 明暗处理(光照)\(\rightarrow\) 光栅化 \(\rightarrow\) 真实感图像
(1) 几何建模
- 用数学方法建立所需三维场景的几何描述
- 通常是由三维造型系统完成
- 场景的几何描述直接影响了图形的复杂性和图形绘制的计算开销
(2) 投影
- 将三维几何描述转换为二维透视图
- 通过对场景的透视变换来完成
(3) 确定形状
- 隐藏面消除
- 确定场景中的所有可见面
- 将视野之外或被其它物体遮挡的不可见面消去
(4) 确定色彩
- 计算场景中可见面的颜色
- 根据基于光学物理的光照明模型计算可见面投射到观察者眼中的光亮度大小和色彩组成,并将它转换成适合图形设备的颜色值,从而确定投影画面上每一象素的颜色(或者与纹理相结合),最终生成图形
简单光照明模型
简单光照明模型的假设
- 仅考虑光源照射在物体表面产生的反射光
- 通常假定物体表面是光滑的且由理想材料构成,只考虑被照明物体的几何对反射和透射光的影响
- 忽略光源的颜色和几何形状(点光源白光照明)
- 可以模拟出不透明物体表面的明暗过渡,具有一定的真实感。 但真实感较差,阴影区域边界尖锐
基础
- 反射
- 理想漫反射(diffuse reflection)
- 镜面高光(specular highlight)
- 环境光
- ambient lighting
- 直接光:直接反射/折射
- 间接光:间接反射/折射
- 简单光照明不考虑间接光
- 以下提到的方向向量均为单位向量
环境光
- 光线在场景中经过复杂传播之后,形成的弥漫于整个空间的光线
- 事实上是不存在的
- 由于难以模拟,假想出来的
- \(I_e=K_aI_a\)
- 物体表面呈现的亮度 = 环境光反射系数 x 环境光亮度
漫反射
- 点光源
- 向周围辐射等强度的光
- 漫反射
- 粗糙、无光泽物体(如粉笔)表面对光的反射
- \(I_d=I_pK_d\cos\theta=I_pK_d(\vec{L}\cdot\vec{N})\)
- 物体表面呈现的亮度 = 点光源的亮度 x 漫反射系数 x \(\cos\)(入射角)
镜面反射与 Phong 模型
- 光滑物体表面,高光效果
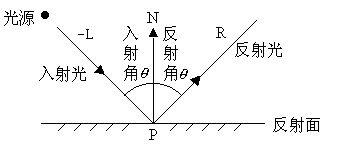
理想镜面反射
- 难以捕获:要求视点恰好在反射光 R 的方向上
- \(\vec{R}=2(\vec{L}\cdot\vec{N})\vec{N}-\vec{L}\)
- \(\vec{R}+\vec{L}=(2|\vec{R}|\cos\theta)\vec{N}=(2\cos\theta)\vec{N}=2(\vec{N}\cdot\vec{L})\vec{N}\)
非理想镜面反射
- 锥形区域:中心轴为 R,圆锥角 \(2\beta\)
- 圆锥内部:光强由中心向四周递减
- 圆锥外部:光强为 0
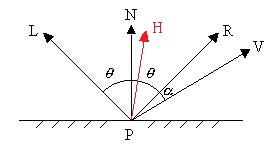
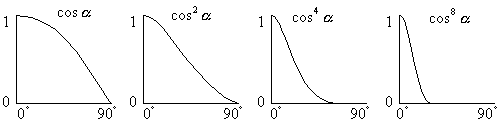
- Phong 模型
- \(I_s=I_pK_s(\cos\alpha)^n=I_pK_s(\vec{V}\cdot\vec{R})^n\)
- n 为镜面反射系数
- n 越大,高光越集中
- 定义 \(\vec{H_0}=\dfrac{1}{2}(\vec{L}+\vec{V}),\vec{H}=\dfrac{\vec{H_0}}{\Vert\vec{H_0}\Vert}=\dfrac{\vec{H_0}}{\cos\theta}\)
- 可以用 \(\vec{H}\cdot\vec{N}\) 代替 \(\vec{V}\cdot\vec{R}\)
- 趋势是一致的
- \(\vec{H}\cdot\vec{N}=\dfrac{\cos\theta+\cos(\theta+\alpha)}{2\cos\theta}\)
- \(\alpha\in[0,\dfrac{\pi}{2}]\to[1,1-\tan\theta]\)
- \(\vec{V}\cdot\vec{R}=\cos\alpha\)
- \(\alpha\in[0,\dfrac{\pi}{2}]\to[1,0]\)
- \(<\vec{H},\vec{N}>=\dfrac{<\vec{V},\vec{R}>}{2}\)
- \(\vec{H}\cdot\vec{N}=\dfrac{\cos\theta+\cos(\theta+\alpha)}{2\cos\theta}\)
光线的衰减
(1) 光在光源到物体表面过程中的衰减
- \(f(d)=\min(\dfrac{1}{c_0+c_1d+c_2d^2},1)\)
- 经验函数
(2) 光在物体表面到人眼过程中的衰减
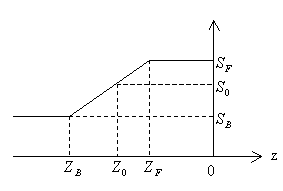
- Depth Cueing 技术(深度暗示技术)
- 使用深度值代替表示距离(几乎等价)
- 线性插值
- front/back:前/后参考面,并且赋予比例因子 \(S_f,S_b\in[0,1]\)
\[ S_0= \begin{cases} S_b,&Z_0<Z_b\\ S_b+\dfrac{Z_0-Z_b}{Z_f-Z_b}(S_f-S_b),&Z_0\in[Z_b,Z_f],\\ S_f,&Z_0>Z_f \end{cases} \]
- \(I'=S_0I+(1-S_0)I_{dc}\)
- \(I_{dc}\) 为融合亮度,是用户指定的
- 特别的:\(S_f=1,S_b=0,I_{dc}=0\)
\[ S_0= \begin{cases} 0,&Z_0<Z_b\\ \dfrac{Z_0-Z_b}{Z_f-Z_b},&Z_0\in[Z_b,Z_f],\\ 1,&Z_0>Z_f \end{cases} \]
\[ I'= \begin{cases} 0,&Z_0<Z_b\\ \dfrac{Z_0-Z_b}{Z_f-Z_b}I,&Z_0\in[Z_b,Z_f],\\ I,&Z_0>Z_f \end{cases} \]
- 衰减为 0 \(\rightarrow\) 部分衰减
\(\rightarrow\) 不衰减
- 真实感较好
简单光照明模型
- \(I=I_aK_a+f(d)I_p[K_d(\vec{L}\cdot \vec{N})+K_s(\vec{V}\cdot\vec{R})^n]\)
- 环境光是不衰减的
彩色
- 选择合适的颜色模型:RGB模型
- 为颜色模型中的每一种基色建立光照明方程
- \(I=I_{a\lambda}K_{a\lambda}+f(d)I_{p\lambda}[K_{d\lambda}(\vec{L}\cdot
\vec{N})+K_{s\lambda}(\vec{V}\cdot\vec{R})^n]\)
- \(\lambda\in\{R,G,B\}\)
多光源
- 为每个光源建立光照明模型
- 注意环境光只有一个
- 如下,\(m\) 个光源
\[ I=I_{a\lambda}K_{a\lambda}+\sum_{i=1}^{m}\{f(d_i)I_{p_i\lambda}[K_{d_i\lambda}(\vec{L_i}\cdot \vec{N})+K_{s_i\lambda}(\vec{V}\cdot\vec{R})^n]\} \]
多边形绘制着色方法
- shading
- 计算完顶点信息之后如何对内部的点上色
- 统一着色(constant shading)
- 均匀着色(flat shading)
- 光滑着色 (smooth shading)
- Gouraud着色方法 (Gouraud shading)
- Phong着色方法 (Phong shading)
统一着色
- constant shading
- 每个物体着同一种颜色
均匀着色
- flat shading
- 每个表面着同一种颜色
- 着色方法
- 任取多边形上一点,利用光照明方程计算出它的颜色
- 用这个颜色填充整个多边形
- 适用情况:同一表面差别不大
- 光源在无穷远处
- 视点在无穷远处
- 多边形是物体表面的精确表示
- 优点
- 每个多边形只需计算一次光照明方程,速度快
- 缺点
- 相邻多边形颜色过渡十分不光滑
光滑着色
- 方法:插值
- 颜色插值 \(\rightarrow\) Gouraud 着色方法
- 法矢量插值 \(\rightarrow\) Phong 着色方法
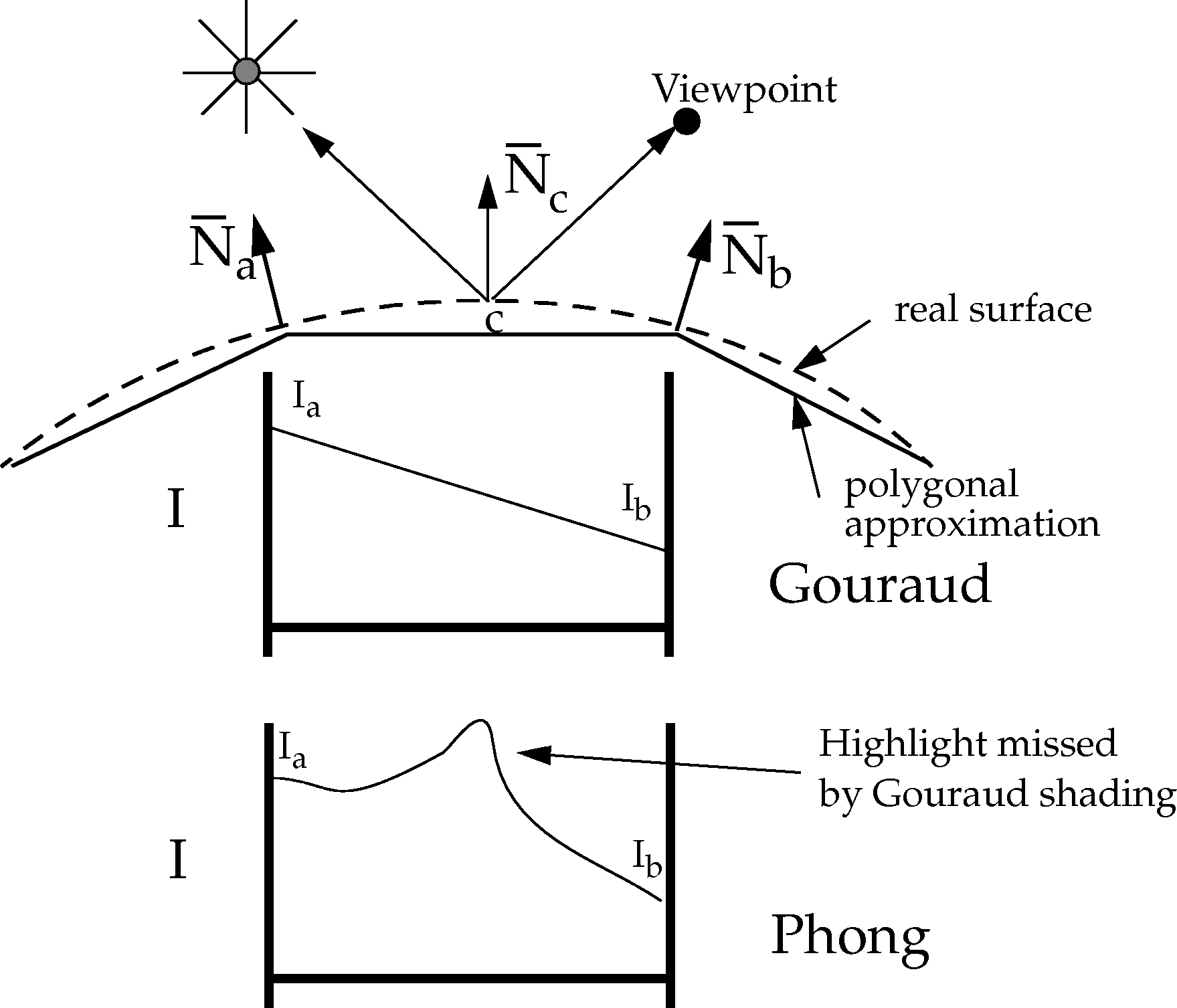
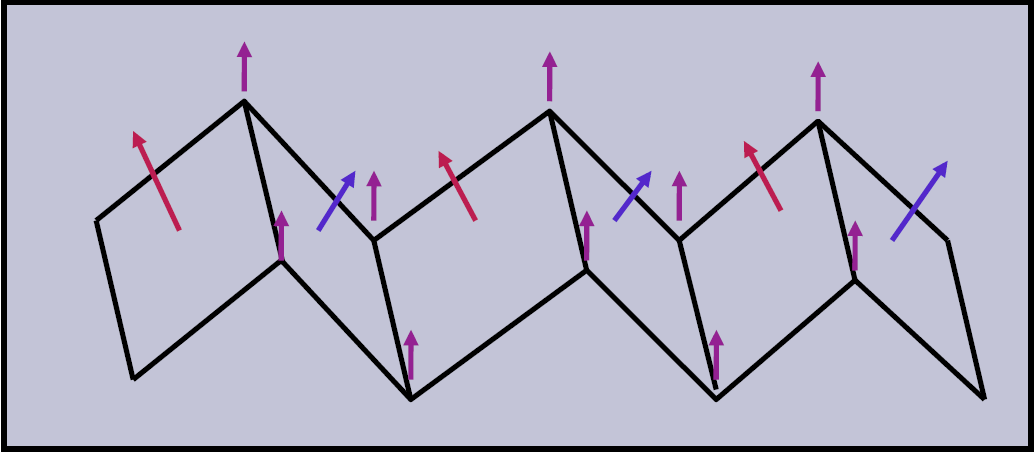
Gouraud 着色方法
- 面法向量 \(\rightarrow\) 顶点法向量 \(\rightarrow\) 计算颜色 \(\rightarrow\) 颜色插值
步骤
- 计算多边形的单位法矢量(面法向量)
- 面内两个向量叉乘
- 计算多边形顶点的单位法矢量(顶点法向量)
- 拟合
- 简单的拟合方式:使用 1 邻域的面法向量的均值
- 1 邻域:直接相邻的面
- 2 邻域:直接相邻的面以及和这些面直接相邻的面
- 利用光照明方程计算顶点颜色
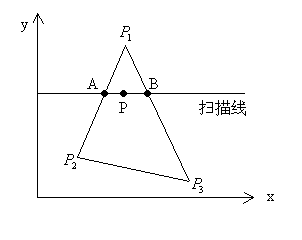
- 对多边形顶点颜色进行双线性插值,获得多边形内部各点的颜色
- 如下图:需要求得点 \(P\) 的颜色
- 第三步求出了顶点 \(P_1,P_2,P_3\) 的颜色
- 通过线性插值求出点 \(A,B\) 的颜色
- 对 \(A,B\) 进行线性插值求得点 \(P\) 的颜色
- 如下图:需要求得点 \(P\) 的颜色
 \[
I_a=I_1\dfrac{y_a-y_2}{y_1-y_2}+I_2\dfrac{y_1-y_a}{y_1-y_2}\\
I_b=I_1\dfrac{y_a-y_3}{y_1-y_3}+I_2\dfrac{y_1-y_a}{y_1-y_3}\\
I_p=I_a\dfrac{x_p-x_a}{x_b-x_a}+I_b\dfrac{x_p-x_a}{x_b-x_a}
\]
\[
I_a=I_1\dfrac{y_a-y_2}{y_1-y_2}+I_2\dfrac{y_1-y_a}{y_1-y_2}\\
I_b=I_1\dfrac{y_a-y_3}{y_1-y_3}+I_2\dfrac{y_1-y_a}{y_1-y_3}\\
I_p=I_a\dfrac{x_p-x_a}{x_b-x_a}+I_b\dfrac{x_p-x_a}{x_b-x_a}
\]
缺点
- 不能正确模拟高光
Phong 着色方法
- 面法向量 \(\rightarrow\) 顶点法向量 \(\rightarrow\)法向量插值 \(\rightarrow\) 计算颜色
步骤
- 计算多边形单位法矢量
- 计算多边形顶点单位法矢量
- 对多边形顶点法矢量进行双线性插值,获得内部各点的法矢量
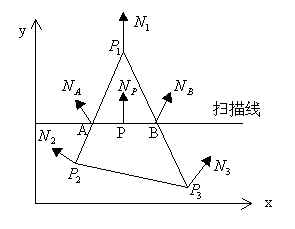
- 利用光照明方程计算多边形内部各点颜色

方法对比
- 计算颜色时期的不同:插值总是在光栅化阶段(rasterization)
- Gouraud:vertex shader
- Phong:fragment shader
- 高光
- Gouraud:缺失
- Phong:还不错
插值方法存在的问题
- 不光滑的物体轮廓
- 模型离散化道中的
- 解决方案:使用法相贴图,将需要求的法向值给定,这样就无需插值拟合
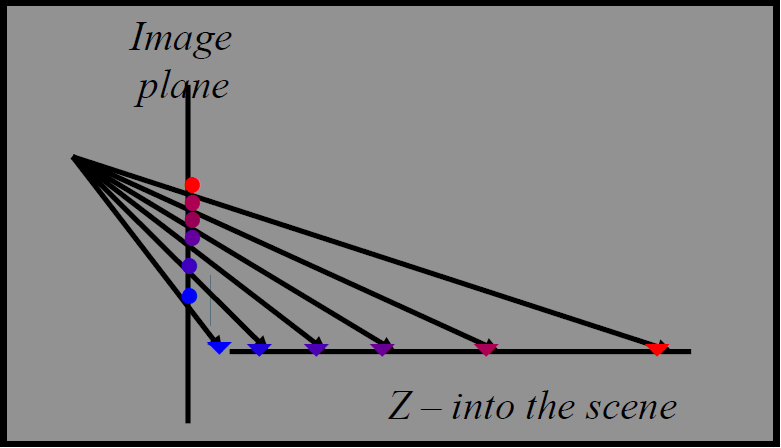
- 透视变形
- 我们的插值是在投影平面上进行的,实际上应该在三维空间中插值
- 这样在趋势上会有所差别
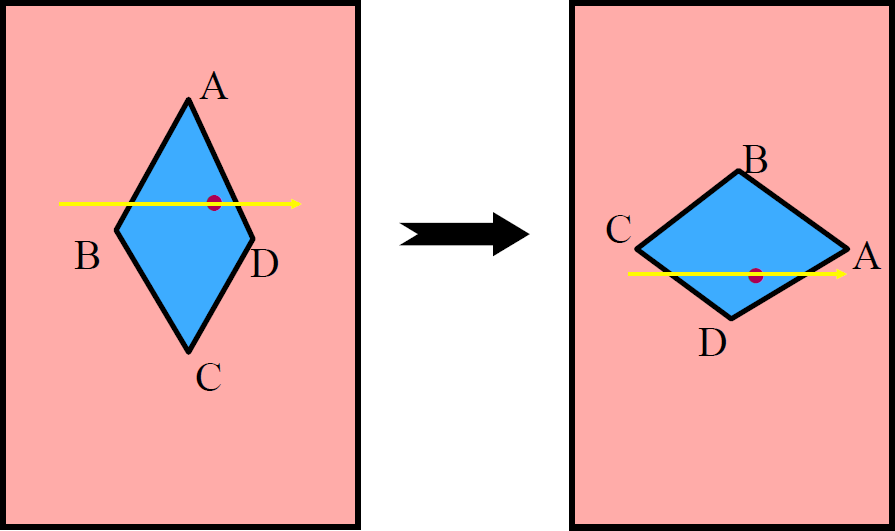
- 方向依赖性
- 双线性插值的方向依赖性
- 早期的问题,现在已经能够解决
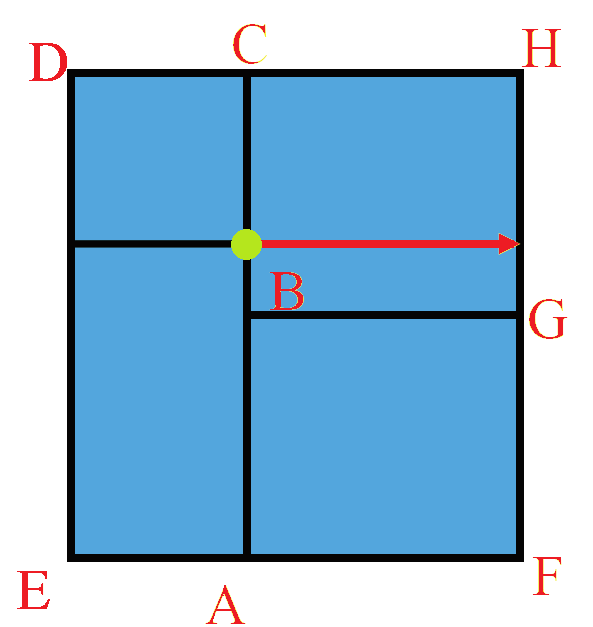
- 公共顶点颜色不连续
- 下图的绿点
- 对于左上角的小矩形来说,是顶点(计算产生)
- 对于右上角的的矩形来说,不是顶点(插值产生)
- 因此其周围的点颜色可能不连续
- 下图的绿点
- 顶点方向不具有代表性
- 如果使用定顶点进行插值,区分不出来两种类型的面(颜色都一样)
- 解决方案:将面进行更加细致的剖分,这样就可以减少这种情况的发生
阴影
- 阴影
- 光源不能直接照射的区域
- 对光源来说,不可见的面(隐藏面)
- 考虑阴影的光照明方程
\[ I=I_{a\lambda}K_{a\lambda}+\sum_{i=1}^{m}\{S_if(d_i)I_{p_i\lambda}[K_{d_i\lambda}(\vec{L_i}\cdot \vec{N})+K_{s_i\lambda}(\vec{V}\cdot\vec{R})^n]\}\\ \]
\[ S_i= \begin{cases} 0,&位于第i个光源的阴影中\\ 1,&else \end{cases} \]
- 简单:点光源
- 复杂:体光源、面光源
基于 GPU 硬件的 shadow map 算法
- 像素级别精确的阴影算法
- 点光源
- 利用 z-buffer 消隐
- 将物体变换到光源坐标系中,消隐,记录下可见的最小深度值(z-buffer)
- 将物体变换到光源坐标系中,计算深度,如果大于记录值则不可见,否则可见(只可能等于)
算法步骤
- 将所有景物变换到光源坐标系中,利用 z 缓冲器算法按光线方向对景物进行消隐,把那些距光源最近的物体表面上点的深度值保存在阴影缓冲器中
- 利用Z缓冲器算法按视线方向对景物进行消隐,将得到的每一个可见点变换到光源坐标系中,若 它在光源坐标系中的深度值比阴影缓冲器中相应单元的值小,则说明该可见点位于阴影中,否则不是
优点
- 算法简单,易于实现
- 已经可以在GPU硬件上直接实现
缺点
- 每个光源需要一个阴影缓冲器
- 在阴影的边界上容易形成锯齿效果
- 量化误差(算法精度、z-buffer大小、深度值精度)
RSM:Reflective Shadow Map
- shadow map 第一次渲染只生成了一张深度图,太浪费(代价太大)
- 第一次渲染的时候同时生成一些其他信息
- 光源直接照到部分的深度 \(\rightarrow\) 光源直接照到部分的深度、颜色、法向
- 第二次绘制利用第一次绘制生成的信息可以计算单次间接光照
阴影反混淆
- 边界锯齿 \(\rightarrow\) 平滑过渡
- 锯齿的光栅化过程产生的
- 走样
- 反走样
- 时域:连续帧中,远方亮点的忽隐忽现(flick)
- 空域:边界锯齿
- 反走样方法
- SSAA:Super Sampling Anti-Aliasing
- 超采样反走样
- 每个采样点进行进一步的细分
- x2,x3,x4 \(\rightarrow\) 每个采样点细分为为 4,9,16个采样点
- MSAA:Multi-Sampling AA
- 多采样反走样
- SSAA 的计算量非常大,SSAA 的改进
- 寻找出物体边缘部分的像素,然后对它们进行超采样处理
- 这样忽略掉了不会产生锯齿的内部像素,减少了计算量
- 光栅化而言,MSAA 跟 SSAA 差不多,覆盖和遮挡信息在更大的分辨率上进行的
- 着色的时候,通过计算原始的一个采样点细分出来的不同采样点的颜色混合得到原始采样点的颜色
- CSAA:Coverage Sampling AA
- 覆盖取样抗锯齿
- TAA
- temporal AA
- SSAA:Super Sampling Anti-Aliasing
- 方法对比
- SSAA 中,每个取样表示了着色颜色、储存的颜色/Z/模板、和覆盖,本质上增加了渲染到一个过大的缓存并向下取样
- MSAA 通过从储存的颜色和覆盖中分离出着色取样,减少了这项操作的着色器开销;这允许应用程序使用抗锯齿来处理更少的着色取样同时维持同样质量的颜色/Z/模板和覆盖取样
- CSAA通过从颜色/Z/模板分离出覆盖进一步优化了这个过程,从而减少带宽和存储开销
- 反走样方法
- 光栅化图形显示必然的问题问题
- trade off(时间与质量)
基于GPU硬件 的 Shadow Volume
- 几何级别精确的阴影算法
- 没有阴影锯齿问题
- 光源 \(\rightarrow\)
物体轮廓
- 光源和轮廓形成的锥体向远处拉伸,形成阴影体
- 关键问题
- 找出轮廓
- 如何判断物体是否处于阴影中
如何判断物体处于阴影体中
- 直接对所有的几何体和阴影体求交、求交线
- 复杂度很高
- 利用 buffer
累积缓冲
思路
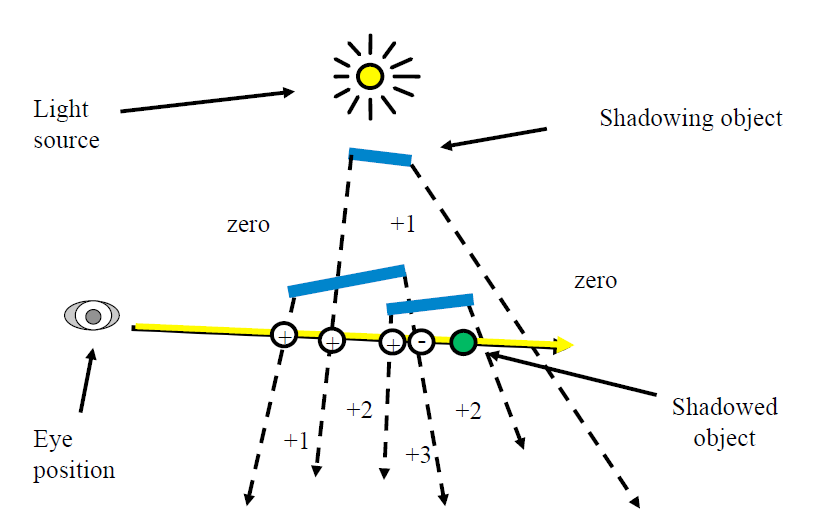
- 光源和物体形成射线
- 视点和需要求的点形成线段(方向为视点到待求的点),在线段上求累积值
- 正向面 +1,负向面 -1
- 朝向视点的面/远离视点的面
- 求累计值
- 若大于 0,则处于阴影中
- 若等于 0,则不在阴影中
怎么形成线段
- 怎么去掉物体之后的视线部分,上述黄线的绿点右边部分
- 绘制顺序、绘制状态
具体步骤
- 绘制出整个场景(非阴影体),确定整个场景的深度(记录到深度缓冲器中)
- 画阴影体(正向面/反向面),顺序没有关系
- 和记录的深度值比较
- 若比记录的小,则根据自己是正向面还是反向面更新累计缓冲值
- 若大,则不更新累计缓冲值
- 只进行深度判断,不进行深度更新(不修改深度缓冲器的值)
- 阴影体是虚拟的,是我们人为加入的
- 和记录的深度值比较
问题(特例)
视点位于阴影体内部
- 解决方法:在视线上,从无穷远到待求的点这条线段上进行累计缓冲计数
- 比较计数的时候,只比较深度大于待求点的阴影体
- z-fail:计数的点是没有通过深度检测的阴影体(解决特例的方法)
- z-pass:计数的点是通过深度检测的阴影体(常规方法)
- 无穷远是客观的(无穷远不在阴影内部)
- 比较计数的时候,只比较深度大于待求点的阴影体
- 问题:无穷远在阴影中,出错
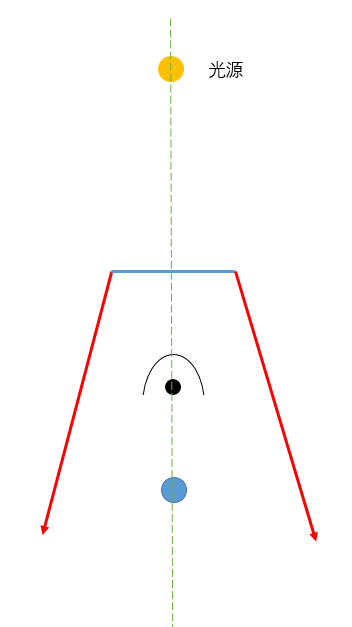
- 解决方法:在视线上,从无穷远到待求的点这条线段上进行累计缓冲计数
视见体把某些物体裁剪掉了,导致阴影体减少了
- 上述算法出错
软影以及动态光源阴影的生成
- 面光源、体光源
- 软影(本影、半影)
- 笨的方法:将光源进行点采样
- 慢,效率低下
- 阴影楔
- A Geometry-based Soft Shadow Volume Algorithm
- 实时图像渲染
- Tomas Akenine-Möller
- A Geometry-based Soft Shadow Volume Algorithm
- 光源形态发生变化(火焰)
- 待渲染的物体变化
透明现象
简单透明
- 简单透明不考虑折射现象
插值透明
- \(I_\lambda=(1-K_{t_1})I_{\lambda_1}+K_{t_1}I_{\lambda_2}\)
- \(K_{t_1}=1\):1 完全透明,2 完全不透明
- \(K_{t_1}=0\):2 完全透明,1 完全不透明
过滤透明
- \(I_\lambda=I_{\lambda_1}+K_{t_1}C_{t\lambda}I_{\lambda_2}\)
- \(K_{t_1}\):透射系数,越大颜色透射得越多
- \(C_{t\lambda}\):不同颜色系数不同
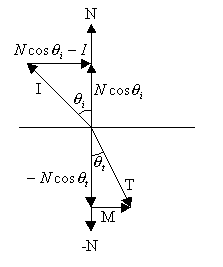
折射
- 折射定律
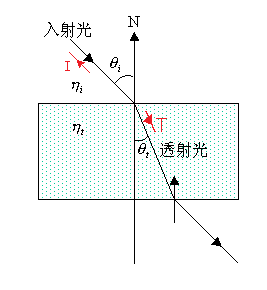
- \(\dfrac{\sin\theta_i}{\sin\theta_t}=\dfrac{\eta_t}{\eta_i}=\dfrac{1}{\eta}\)
- \(\vec{T}=(\eta\cos\theta_i-\cos\theta_t)\vec{N}-\eta\vec{I}\)