计算机图形学.李胜.07.三维实体的表示

表示形体的两种模型

数据模型

• 完全以数据表示
  • 例如：以 8 个顶点表示的立方体，以半径和中心表示的球体
  • 以数据文件的形式存在
  • 包括
    • 特征表示、空间分割表示、推移表示、边界表示、构造实体集合表示等

(1) 线框模型

• 将形体表示成一组轮廓线的集合
• 简单、处理速度快
• 与形体之间不存在一一对应关系，是真实物体的高度抽象、不适合真实感显示

(2) 表面模型

• 将形体表示成一组表面的集合
• 形体与其表面一一对应，适合真实感显示

(3) 实体模型

• 用来描述实体，主要用于 CAD/CAM
• 包含了描述一个实体所需要的较多信息（几何信息、拓扑信息等）

过程模型

• 以一个过程和相应的控制参数描述
• 例如：用一些控制参数和一个生成规则描述的植物
• 以一个数据文件和一段代码的形式存在
• 包括
  • 粒子系统、L系统、迭代函数系统

实体的定义

• 抽象带来的问题

  • 计算机中的数学方法表示的物体可能无效
  • 不能够客观存在
    • CAD / CAM 需要客观存在

• 客观存在（有效）—— 实体的定义

  • 具有一定的形状
  • 具有封闭的边界（表面）
  • 内部连通
  • 占据有限的空间
  • 经过运算之后仍是有效的实体

• 实体看作点集（使用集合论的方法描述）

  • 内点：具有完全包含于该点集的充分小的领域的点
  • 边界点：物体上除了内点之外的点
  • 取内点运算：\(i\)
  • 取闭包运算：\(c\)
  • 正则运算：\(r\)
    • 先取内点，再取闭包
    • \(r\cdot A=c\cdot i\cdot A\)
    • 一个例子

  

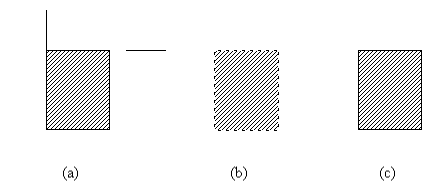
  • 正则点集 \(A\) 满足 \(r\cdot A=A\)

• 正则点集一定是实体吗？不一定

  • 内部不连通

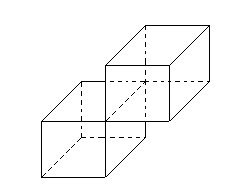
• 实体可计算的条件
  • 正则点集
  • 表面是二维流形
    • 二维流形：其上任意一点存在充分小的领域与平面圆盘同构（存在连续的一一映射）
  • 同构
    • 内点 \(\cong\) 圆盘
    • 边界点 \(\cong\) 半圆盘

正则集合运算

为什么需要正则集合运算

• 集合运算式构造物体的有效方法
• 普通的集合运算会产生无效物体

正则并/交/差

正则运算定义

• \(A\ op^\star\ B=r\cdot(A\ op\ B)\)
• 正则并：\(A\cup^\star B=r\cdot(A\cup B)\)
• 正则交：\(A\cap^\star\ B=r\cdot(A\cap B)\)
• 正则差：\(A-^\star\ B=r\cdot(A-B)\)

边界 bS

• 内部 \(iS\)，边界 \(bS\)，外部 \(eS\)
• \(S=bS\cup iS\)

求边界确定实体

• \(bA=(bA\cap iB)\cup(bA\cap bB)\cup(bA\cap eB)\)
• \(bB=(bB\cap iA)\cup(bB\cap bA)\cup(bB\cap eA)\)
• 公共边界 \(bA\cap bB=bB\cap bA\) 可以分为两个部分
  • 同侧：实体 A 和 B 位于边界的同侧
  • 异侧：实体 A 和 B 位于边界的异侧
  • \(bA\cap bB=(bA\cap bB)_{同侧}\cup(bA\cap bB)_{异侧}\)
• 通过讨论边界的组成得到以下结论
  • 正则并
    • \(b(A\cup^\star B)=(bA\cap eB)\cup(bB\cap eA)\cup(bA\cap bB)_{同侧}\)
  • 正则交
    • \(b(A\cap^\star B)=(bA\cap iB)\cup(bB\cap iA)\cup(bA\cap bB)_{同侧}\)
  • 正则差
    • \(b(A-^\star B)=(bA\cap eB)\cup(bB\cap iA)\cup(bA\cap bB)_{异侧}\)

特征表示

• 用一组特征参数表示一组类似的物体
• 特征包括形状特征、材料特征等
• 适用于工业上标准件的表示
• 例子
  • 圆柱体：R，H
  • 立方体：边长a

空间分割表示

(1) 空间枚举表示

• 选择一个立方体空间，将其均匀划分
• 使用三维数组表示物体，数组中的元素与单位小立方体一一对应
  • 1/0：是否被物体占据
• 优点
  • 可以表示任何物体
  • 容易实现物体间的集合运算
  • 容易计算物体的整体性质，如体积等
• 缺点
  • 占据大量的存储空间
  • 没有边界信息，不适于图形显示
  • 对物体进行几何变换困难，例如非90度的旋转
  • 是物体的非精确表示
    • 量化走样

(2) 八叉树

• 对空间位置枚举表示的空间分割方法做了改进
  • 均匀分割 \(\rightarrow\) 自适应分割
• 对绘制有好处

八叉树的建立

• 根结点对应整个物体空间
• 从根结点开始，对于一个结点
  • 如果该结点完全被物体占据则记为 \(F\)（Full）
  • 如果该结点内部没有物体则记为 \(E\)（Empty）
  • 如果被物体部分占据则记作 \(P\)（Partitial）
    • 同时将其分割为 8 个立方体，每个立方体作为一个新的结点，进行同样的操作

八叉树的应用

• Voxel based GI：基于八叉树的全局光照明
• SVOGI：Sparse Voxel Octree Global Illumination
  • 全局光渲染
• Voxelization（体素化）
  • 将物体的几何形式表示转换成最接近该物体的体素表示形式，产生体数据集
  • 不透明度属性/法向/发光向/材质/······
• 待渲染场景 \(\rightarrow\) 体素化 \(\rightarrow\) 八叉树构造

cone tracing

• 结合八叉树
• 点向周围展开圆锥（立体角）
• 全局光照明：计算间接光照的时候，使用圆锥内的光照进行近似
  • 在圆锥中，根据大小找到对应的不同粒度的八叉树，使用保存的属性
  • 不同粒度，八叉树最小结点的大小不同（层次）

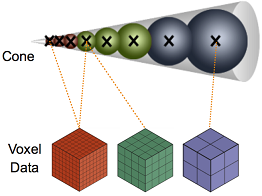
• 求光照
  • 蒙特卡洛采样积分：复杂度高
  • core tracing：复杂度相对较低

八叉树评价

• 优点
  • 可以表示任何物体
  • 容易实现物体间的集合运算
  • 容易计算物体的整体性质，如体积等
  • 相较于空间位置枚举表示占用的存贮空间少
• 缺点
  • 没有边界信息，不适于图形显示
  • 对物体进行几何变换困难，例如非90度的旋转
  • 是物体的非精确表示

(3) 单元分解表示

• 对空间位置枚举表示的空间分割方法做了改进
  • 单一体素 \(\rightarrow\) 多种体素

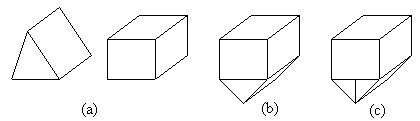
• 优点
  • 表示简单
  • 容易实现几何变换
  • 基本提速可以按需选择，表示范围较广
  • 可以精确表示物体
• 缺点
  • 物体表示不唯一
  • 物体有效性难以保证

空间层次划分

KD-Tree

• 适合静态场景的光线追踪
• 降低算法查找的复杂度
  • 静态：一次建立，多次查找
  • \(\log n\)
• 只进行横向和纵向的划分
  • 分割线只有水平和竖直
• KD-Tree 降低了每一步判断在哪一个区域的复杂度
  • 只需要和某几个维度比较（降维）
• 判断点在分割线的哪个部分（2D）
  • 任意直线：\(ax+by+c\) 和 \(0\) 作比较
  • KD-Tree：
    • 水平：\(x\) 和 \(0\) 作比较
    • 竖直：\(y\) 和 \(0\) 作比较

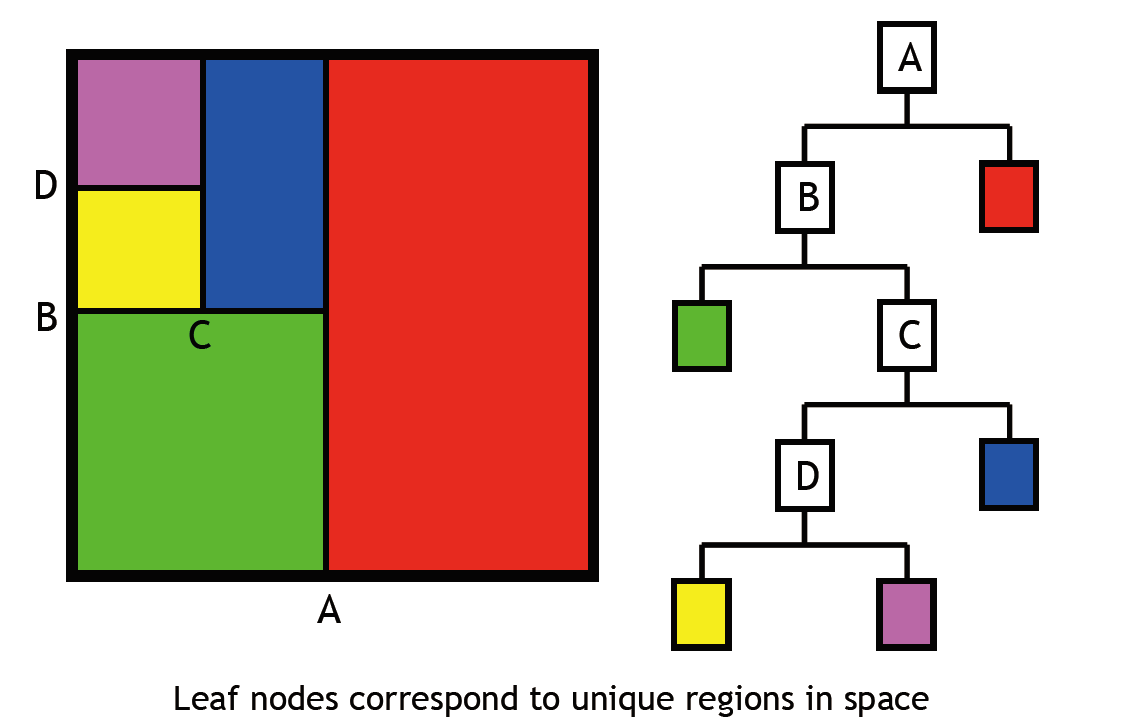
• 基于 kd-tree 的光子映射算法 photon mapping
  • 给定一个点（位置），搜索在某个邻域之内散落的光子
  • KNN 的方法
  • KD-Tree 能够很好支持

BVH 层次包围盒

• Bounding Volumn Hierarchy
• 适合动态场景的表示以及碰撞检测

推移表示

• sweep 体（扫掠）
  • 将物体 A 沿着轨迹 P 推移得到物体 B，称 B 为 sweep 体
• 平移 sweep
  • 将一个二维区域沿着一个矢量方向推移
• 旋转 sweep
  • 将一个二维区域绕旋转轴旋转一周
• 广义 sweep
  • 任意物体沿着任意轨迹推移
  • 推移过程中物体可以变形
• 优点
  • 表示简单、直观
  • 适合做图形输入手段
• 缺点
  • 做集合运算困难，正则集合运算下非封闭
• 应用
  • CAD 中工件的表示

边界表示

• 思想：物体的边界与物体一一对应，确定了物体的边界也就确定了物体本身
• 用于表示物体边界的有平面多边形、曲面片
• 平面多边体
  • 表面由平面多边形组成的多面体
  • 严格要求每条边只属于两个多边形
• 简单多面体
  • 与球拓扑同构
• 欧拉公式：\(V-E+F=2\)
  • 顶点数 - 边数 + 面数 = 2
  • 图论角度，从树开始推导

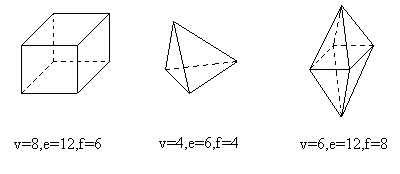
• 欧拉公式是实体的必要条件
  • 其他条件：边共享，顶点共享
  • 一条边只能被两个面共享（\({\color{red}2}\)）

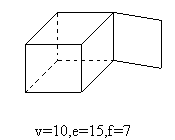
• 广义欧拉公式：\(V-E+F-R=2(S-H)\)
  • 顶点数 - 边数 + 面数 - 孔的个数 = 2(体的个数 - 洞的个数)
  • 孔和洞的区别在于洞是贯穿的
  • 非简单多面体

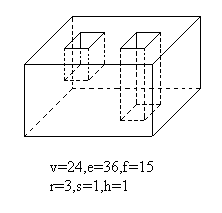
• torus：亏格
  • 面包圈形态：亏格为1（\(H=1\)）
  • 亏格为0的实体可以和球同构
• 多边形的顶点顺序与法向量
  • 规定一个顶点顺序，确定法向量
  • 法向量：正反面，光照，几何计算等
• 空间多边形的平面方程计算
  • 顶点可能不共面：最小二乘法 拟合出一个平面，使其到所有顶点的距离之和最小
• 边界表示的数据结构
  • 半边结构
    • 一条边当作两条半边
    • 好处
      • 确定边的方向
      • 确定一个边的搜索顺序
      • 确定边被哪些平面共享
        • 在几何造型时有用，单纯显示没有必要
        • 例如删除某个平面，此时相关联的边也需要修改（修改拓扑结构）
    • 下图：方向为规定的正方向，红色为半边的方向

• 边界表示优点
  • 精确表示物体
  • 表示能力强
  • 几何变换容易
  • 适于显示处理
• 边界表示缺点
  • 表示复杂
  • 有效性难以保证
  • 集合运算复杂

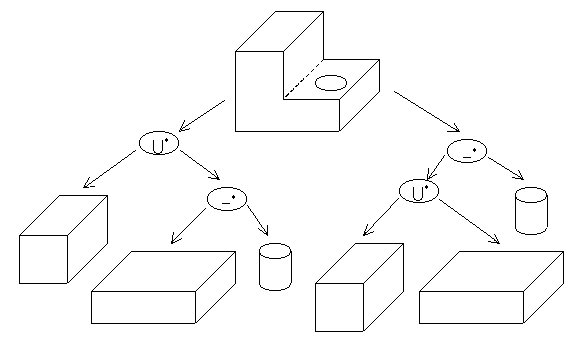
构造实体的几何表示

• 将物体表示成一棵二叉树，CSG树
• 叶节点：基本体素
  • 立方体，圆柱体等
• 中间节点：正则运算集合
  • 并交差

• 面
  • 环
  • 边
    • 半边（1，2）
• 优点
  • 表示简单、直观
  • 是物体的构造方法，可用作图形输入手段
  • 容易计算物体的整体性质
  • 物体的有效性自动得到保证
• 缺点
  • 表示不唯一
  • 不能直接用于显示
  • 求交计算麻烦

不规则形体的建模方法

• 迭代函数系统
• 基于文法的模型
• 粒子系统

迭代函数系统

• IFS：Iterated Function System
• 分形
• 具有 5 个基本特征
  • 形态的不规则性
  • 结构的精细性
  • 局部与整体的自相似性
  • 为数的非整数性
  • 生成的迭代性

L 系统

• 由生物学家 Lindenmayer 创立
• 基本思想
  • 用文法表示植物的拓扑结构
    • BNF
  • 通过图形学的方法生成逼真的画面
• DOL系统（确定的上下文无关的L系统）
  • 定义为三元组 \(<V,w,P>\)
    • \(V\) 表示字母集合，字母表
    • \(Y^\star\) 表示 \(V\) 上的所有单词的集合
    • \(w\) 是一个非空单词（\(V\) 中元素的非空排列，称为公理）
    • \(P\) 产生式集合
      • \(\forall a\in V,\exists x\in V^\star\) 使得 \(a\to x\)
        • 有且只有（唯一）的 \(x\)
      • 若无明显的产生式，则令 \(a\to a\)

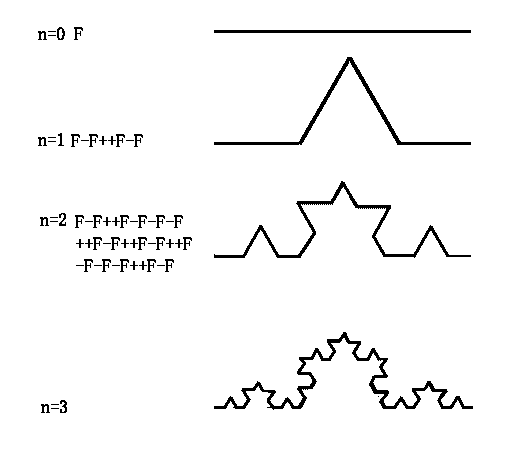
Koch 雪花

• \(V:\{F,+,-\}\)
• \(w:F\)
• \(P:F\to F-F++F-F\)
• 几何解释：
  • \(F\)：向前画一条直线
  • \(+\)：右转 \(\alpha\)
  • \(-\)：左转 \(\beta\)

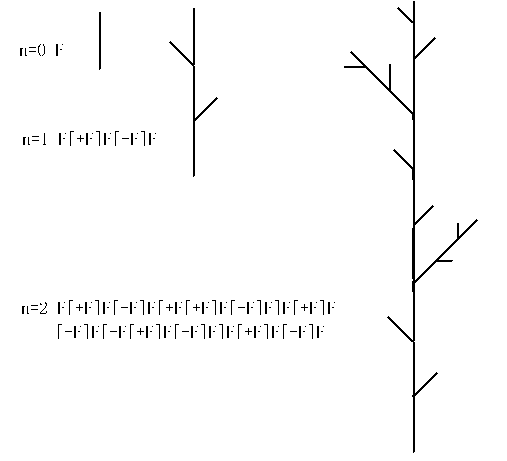
Bracketed L系统

• \(V:\{F,+,-,[,]\}\)
• \(w:F\)
• \(P:F\to F[+F]F[-F]F\)
• 几何解释：
  • \(F\)：向前画一条直线
  • \(+\)：右转 \(\alpha\)
  • \(-\)：左转 \(\beta\)
  • \([\)：压栈
  • \([\)：出栈

粒子系统

Particle Systems

• simulate and render objects / phenomena that do not have clear surface definitions
  • fire, water, snow, explosion, smoke, swarm, fountain ...
    • 火焰、水、雪、爆炸、烟雾、群、喷泉
• Particles are entities (e.g.points) with attributes acting independently and collectively
  • 带有属性的实体，实体之间的属性相互独立或联系
• Typical attributes: position, velocity, color, life span, etc.
  • 位置、速度、颜色、生命周期

一些特点

• An object is represented as clouds of primitive particles that define its volume.
  • 单个粒子很简单，物体的形态由集群的粒子表现
• dynamic, changing form and moving with the passage of time.
  • 动态的、变化的，处于不同生命周期时间段的例子有不一样的状态
• Object is not deterministic, its shape and form are not completely specified.
  • 非确定性的，形状或者样式不是完全规定好的
• Different force rules and different renderings give all the different types of behaviors.
  • 例字在面对不同的条件或者规则会有不一样的行为

粒子的属性

• Position：位置
  • the change of the particle position is affected by its velocity
• velocity：速度
  • affected by force/acceleration
• Lifetime：生命周期
  • the remain life time before the extinction of the particle
  • It is decremented every frame.
  • It may affect may other attributes
• Size：大小
  • may vary during its life span
• Weight：质量
  • useful to calculate acceleration from force
• Visual representation：可视化形式
  • 3D points：3D 的点，适用于比较远的点（看不出来差异）
    • for remote scene
  • Lines：线（粒子轨迹）
    • a trace of particle trajectory
  • Texture-mapped quads：带纹理的四边形
    • very flexible & widely used
• Color：颜色
  • may change during its life span

粒子的集群控制

• Particle list：粒子的列表
• Particle generation：粒子的产生
  • Position：位置信息
    • default, Random or fixed.
  • Emission rate：生成速率
    • how often particles are created.
  • Default particle attributes：初始属性
    • Random or fixed.
• Particle kill：粒子的湮灭（生命周期）
  • kill particles if their lifetimes become 0 or certain conditions happen
• Particle Animation：粒子的动画（每一帧的动画）
  • The remaining particles are moved and transformed according to their dynamic attributes.
• Rendering：渲染器
  • An image of the particles is rendered in the frame buffer, often using special purpose algorithms.
• Force field：交互，外界的影响 affector
  • assign a force (can be different) to each particles to produce acceleration

其他

• 与环境交互
  • 火焰吹风，得动起来
  • 小球沿着坡滚下来
• 粒子的行为
  • 行为规则（内在）
  • 环境（外在，交互）
• 粒子湮灭
  • Lifetime decremented each frame, particle is killed when it reaches zero
  • Kill particles that no longer contribute to image (transparency below a certain threshold, etc.).
• 粒子系统很好玩，但是很难做
  • 粒子系统引擎
  • 交互式编辑（灵活、泛化）
  • 给定一个任意场景（环境因素）
    • 给定一个山形，构建一个符合这个山形的瀑布（很难）